双感应测井资料自适应正则化反演

于　涛

( 大庆钻探工程公司 测井公司，黑龙江 大庆　163412 )



双感应测井资料自适应正则化反演

于涛

( 大庆钻探工程公司 测井公司，黑龙江 大庆163412 )

为了准确获得地层真电阻率，确定地层侵入关系，将非线性反演理论与Morozov偏差原理结合，建立双感应测井(Dual-Induction Log)资料的自适应正则化全参数反演算法。首先根据Tikhonov正则化反演理论，将双感应测井资料反演问题变为含稳定泛函非线性目标函数极小化问题；再利用Gauss-Newton算法确定极小化解。在测井资料的最佳拟合迭代过程中，将Morozov偏差原理及Cholesky分解技术结合，建立一套自适应选择正则化因子方法；最后对大庆油田的实际测井资料进行反演处理。反演结论与试油结果表明,该算法在处理薄层、薄互层时能够取得更为满意的效果。

自适应正则化反演； Morozov偏差原理； 稳定泛函； Fréchet导数； 双感应测井

0　引言

电阻率测井作为一种有效的地质勘探工具和识别含油气地层手段，成为地球物理工作的重点研究对象。其中感应测井是利用电磁感应的原理测量地层电导率的方法，并且同时采用聚焦线圈系和反褶积滤波技术使得它具有良好的纵向和径向探测特性。双感应测井仪器与球型聚焦测井仪器组合，被广泛应用在中、低电阻率地层剖面淡水泥浆井中。当地层水矿化度较钻井泥浆滤液高、储层有侵入的情况下，基本遵循泥浆增阻侵入原则，理论上可以根据深、中感应视电阻率的相对大小进行油水层识别。对于平均厚度低于1 m的薄储层或侵入较深的储层，受井眼周围复杂环境和仪器自身限制等因素影响，双感应测井仪器难以准确探测地层真电阻率，直接应用视电阻率资料计算油气含量，将严重干扰储层参数计算的质量，并且视电阻率的相对大小不能反映真实储层的实际侵入特征[1-2]。双感应测井具有探测深度深、仪器响应受泥浆电阻率变化影响不敏感，以及对地层电阻率变化的非线性响应弱等特点，因此通过消除各种不利因素对双感应测井曲线响应的干扰，从而能在视电阻率曲线中提取地层电阻率的真值和侵入带电阻率具有重要意义。

人们提出一种自动选择正则化因子的迭代反演算法[3-11]，将Tikhonov正则化反演理论[12-25]与Morozov偏差原理[26-27]结合，通过引入非二次稳定泛函限定求解区域的变化范围，自适应选择正则化因子保证目标函数和测井响应、输入资料和模拟响应误差最小，从而提高反演的稳定性和可靠性。笔者采用自适应正则化全参数反演算法，对大庆油田部分区块的双感应测井资料进行反演处理，并与试油结果进行对比，多数试油层段的反演结果与试油结果一致，反演效果较为理想。

1　迭代正则化反演算法与流程

(1)

根据Tikhonov正则化反演理论，双感应测井资料反演问题可转化为求取目标函数J(m)的极小值问题：

(2)

在m(l)的微小邻域内对目标函数J(m)进行Taylor展开，仅保留δm的二次项：

(3)

(4)

则新的模型参数可表示为

(5)

重复运算方程(3-5)，直到满足收敛条件，即可确定地层模型真值m*。为了确保模型初值落在收敛域内，降低初始模型误差对反演结果的影响，采用人机交互分层软件，确定模型参数初值，实现由较少迭代次数获得较高反演精度的目地[3-6]。实际资料处理结果表明，迭代10次基本能够满足收敛条件。双感应测井资料反演流程见图1。

图1　双感应测井资料反演流程Fig.1　Inversion of dual induction logging data

2　正则化因子

正则化因子的选取是整个反演过程的关键，需要将Morozov偏差原理和Cholesky分解技术结合，建立一套自适应选择正则化因子的方法。

(6)

(7)

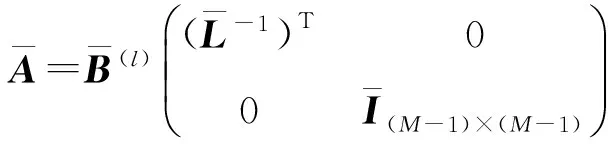
(8)

由式(8)可得模型向量m的第l+1次校正量δm(l)。

设定数据误差后，由Morozov偏差原理可自适应选择合适的正则化因子。由式(3)可得：

(9)

正则化因子α是δ的函数，而δm(α)满足偏差方程：

(10)

由Newton迭代法确定方程(10)的解：

(11)

式中：η′(αp)为η(α)对α的导数，即

(12)

其中式(7)直接对α求导得到δm′(α)：

(13)

3　现场资料处理

大庆油田西部朝长及徐升区块的砂层单层厚度薄且层数多，平面连续性差，给油水层划分及识别带来困难。首先采用人机交互分层软件对曲线进行预处理[4]，在得到地层初始模型的同时提高曲线分辨率；然后由自适应正则化反演软件对区块内50余口井的双感应测井资料进行处理，结果与试油结果符合率达到80%以上，验证文中算法的有效性。

大庆油田A井1 576.0～1 589.0 m深度段的12条常规曲线和双感应反演结果见图2。A井采样的间距和井眼泥浆的电阻率分别为0.051 m和3.0 Ω·m。由图2可知：1 581.0～1 583.4 m深度段常规测井曲线显示地层物性好，电阻率高，而双侧向测井曲线表现为无侵，具有一定的含油特征。在没有邻井处理结果和录井资料情况下，可能将它解释为油水同层，而试油结果表明该深度段含有一个高产工业油层，测井资料解释结果与试油结果不一致。双感应测井曲线显示高侵特征，且自然电位负异常幅度较大，含水特征明显。根据双感应测井资料反演结果，该层段冲洗带电阻率的反演结果Rxo—ivt低于原状地层电阻率的反演结果Rt—ivt，表现为低侵油层特征，较好地恢复地层的真实侵入关系，验证反演算法的有效性和准确性。按照双感应测井资料反演得到的地层模型，重新计算深、中感应曲线(RILD—M和RILM—M)，结果与实测深、中感应视电阻率曲线吻合较好，验证反演算法的可信性。

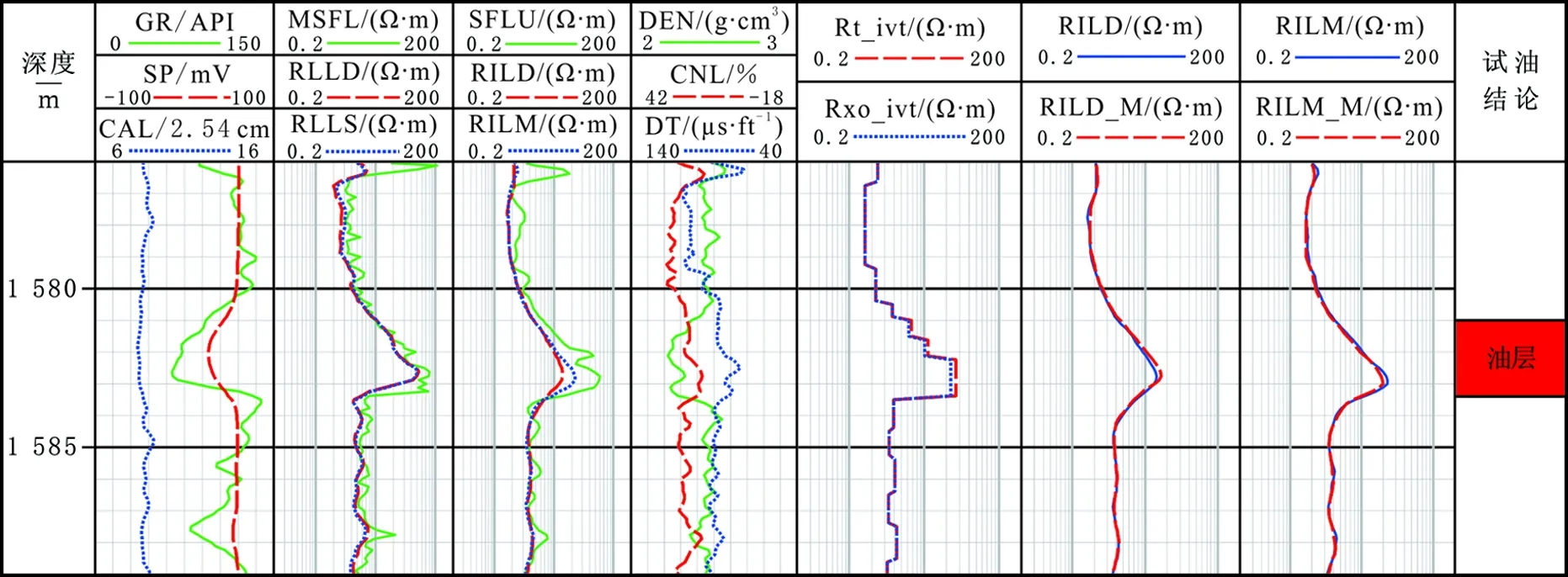
图2　大庆油田A井常规测井资料及双感应测井资料反演结果

大庆油田B井1 936.0～1 966.0 m深度段的12条常规测井曲线和双感应反演结果见图3，采样间距和井眼泥浆的电阻率与A井的相同。由图3可知：该深度段的三段试油结果为水层，而双侧向曲线显示整个层段为低侵特征。双感应曲线显示除了1 939.4和1 959.2 m附近的高阻地层为高侵特征外，其余层段为无侵特征，反演结果表明各个试油段均为明显高侵特征，可以较好地识别水层。

图3　大庆油田B井常规测井资料及双感应测井资料反演结果

4　结论

(1)在层状非均质地层中，引入非二次稳定泛函和自适应选择正则化因子，研究双感应测井资料的自适应迭代正则化反演算法，重构地层的原状电阻率、侵入半径、侵入带电阻率和层界面位置及井眼泥浆电阻率。

(2)比较其他反演算法，文中算法反演结果的可靠性和稳定性得到有效提高，原状地层电阻率与地层电阻率真值更接近，冲洗带电阻率和原状地层电阻率更能反映地层的真实侵入特征，能够为正确识别油水层提供指导。

References) ：

[1]张建华,刘振华,仵杰.电法测井原理与应用[M].西安:西北大学出版社,2002.

Zhang Jianhua, Liu Zhenhua, Wu Jie. Electrical logging principle and application [M]. Xi'an: Northwestern University Press, 2002.

[2]斯伦贝谢测井公司.测井解释原理与应用[M].北京:石油工业出版社,1991.

Schlumberger Logging Company. Logging interpretation principle and application [M]. Beijing: Petroleum Industry Press, 1991.

[3]汪宏年,陶宏根,王桂萍,等.双感应测井资料的快速近似迭代反演[J].地球物理学报,2007,50(5):1614-1622.

Wang Hongnian, Tao Honggen, Wang Guiping, et al. A fast approximate iterative inversion technique of dual induction logging data [J]. Chinese Journal of Geophysics, 2007,50(5):1614-1622.

[4]张玲玲.双感应测井资料的正反演理论及其在大庆油田的应用[D].长春:吉林大学,2007.

Zhang Lingling. Numerical modeling and inversion of dual induction well logging data and their application in Daqing oilfield [D]. Changchun: Jilin University, 2007.

[5]陶宏根,李庆峰,王桂萍,等.双感应测井资料实用化快速近似迭代反演技术及其在大庆油田的应用[J].测井技术,2007,31(5):441-444.

Tao Honggen, Li Qingfeng, Wang Guiping, et al. A practical fast iterative inversion technique of dual induction logging data and its application in Daqing oilfield [J]. Well Logging Technology, 2007,31(5):441-444.

[6]汪宏年,陶宏根,王桂萍,等.从双感应测井录中提取原始视电导率的一种改进方法[J].测井技术,2007,31(3):236-240.

Wang Hongnian, Tao Honggen, Wang Guiping, et al. An improved method to extract the original apparent conductivity from the dual induction log [J]. Well Logging Technology, 2007,31(3):236- 240.

[7]姚东华,汪宏年,陶宏根等. 水平层状介质中双侧向测井资料的迭代Tikhonov正则化反演[J]. 地球物理学报,2010,53(9):2227-2236.

Yao Donghua, Wang Hongnian, Tao Honggen, et al. Iterative Tikhonov regularization inversion of bilateral normal logging data in horizontal layered media [J]. Chinese Journal of Geophysics, 2010,53(9):2227-2236.

[8]姚东华.双侧向测井资料迭代正则化反演与各向异性地层多分量感应测井数值仿真[D].长春:吉林大学,2010.

Yao Donghua. Study the iterative regularization inversion of dual laterolog datum and the numerical simulation of multicomponent induction logging responses in general anisotropic formations [D]. Changchun: Jilin University, 2010.

[9]汪宏年,杨善德,常明澈.水平层状介质中侧向电阻率测井快速迭代反演与应用[J].地球物理进展,1998,13(4):97-107.

Wang Hongnian, Yang Shande, Chang Mingche. The fast nonlinear inversion of laterolog for the horizontal layers and its application [J]. Progress in Geophysics, 1998,13(4):97-107.

[10]汪宏年,陶宏根,其木苏容,等.水平层状介质中双侧向资料的全参数正则化迭代反演与应用[J].地球物理学报,2002,45(增刊):387-399.

Wang Hongnian, Tao Honggen, Chemid Surong. Regularized entire-parameter iterative inversion of dual laterolog in horizontally stratified media and its application. [J]. Chinese Journal of Geophysics, 2002,45(Suppl):387-399.

[11]Wang H N, Yang S D. A multiparameter iterative inversion of dual-laterolog in horizontally layered medium and its error analysis [J]. IEEE Transactions on Geoscience and Remote Sensing, 2002,40(2):482-493.

[12]肖庭延,于慎根,王彦飞.反问题的数值解法[M].北京:科学出版社,2006.

Xiao Tingyan, Yu Shengen, Wang Yanfei. Numerical solution of the inverse problem [M]. Beijing: Science Press, 2006.

[13]王彦飞.反演问题的计算方法及其应用[M].北京:高等教育出版社,2007.

Wang Yanfei. The calculation method and application of the inverse problem [M]. Beijing: Higher Education Press, 2007.

[14]Kirsch A. An introduction to the mathematical theory of inverse problem [M]. New York: Springer Verlag, 1996.

[15]Früauf F, Scherzer O, Leitão A. Analysis of regularization methods for the solution of ill-posed problems involving discontinuous operators [J]. SIAM Journal on Numerical Analysis, 2005,43(2):767-786.

[16]Hansen P C, O'Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems [J]. SIAM Journal on Scientific Computing, 1993,14(6):1487-1503.

[17]Burger M, Kaltenbacher B. Regularizing newton-kaczmarz methods for nonlinear ill-posed problems [J]. SIAM Journal on Numerical Analysis, 2007,44(1):153-182.

[18]Kaltenbacher B. Regularization by truncated Cholesky factorization: A comparison of four different approaches [J]. Journal of Complexity, 2007,23:225-244.

[19]Kaltenbacher B. Some Newton-type methods for the regularization of nonlinear ill-posed problems [J]. Inverse Problems, 1997,13:729-753.

[20]Haber E,Oldenburg D. A GCV based method for nonlinear ill-posed problems [J]. Computational Geosciences, 2000,4:41-63.

[21]Wang J J, Li G S. A Modified Tikhonov regularization method for solving ill-posed problems [J]. Chinese Quarterly Journal of Mathematics, 2000,15(2):98-101.

[22]Neubauer A. Tikhonov regularisation for non-linear ill-posed problems: Optimal convergence rates and finite-dimensional approximation [J]. Inverse Problems, 1989,5:541-557.

[23]Honerkamp J, Weese J. Tikhonovs regularization method for ill-posed problems [J]. Continuum Mechanics and Thermodynamics, 1990,2:17-30.

[24]Lu S, Pereverzev S V, Ramlau R. An analysis of Tikhonov regularization for nonlinear ill-posed problems under a general smoothness assumption [J]. Inverse Problems, 2007,23:217-230.

[25]Bökmann C, Pornsawad P. Iterative Runge-Kutta-type methods for nonlinear ill-posed problems [J]. Inverse Problems, 2008,24,doi:10.1088/0266-5611/24/2/025002.

[26]Scherzer O, Linz. The use of Morozov' discrepancy principle for Tikhonov regularization for solving non-inear ill-osed problems [J]. Computing, 1993,51:45-60.

[27]Bonesky T. Morozov's discrepancy principle and Tikhonov-type functionals [J]. Inverse Problems, 2009,25,doi:10.1088/0266-5611/25/1/ 01501528.

[28]Routh P S,Oldenburg D W. Inversion of controlled source audio-frequency magnetotellurics data for a horizontally layered earth [J]. Geophysics, 1999,64(6):1689-1697.

2015-12-11；编辑：任志平

于涛(1987-)，男，工程师，主要从事测井资料采集与综合解释方面的研究。

10.3969/j.issn.2095-4107.2016.03.003

P613.81

A

2095-4107(2016)03-0018-06