数形结合思想在高中数学教学中的应用与分析
杨斐(安徽省淮北市实验高级中学)
数形结合思想在高中数学教学中的应用与分析
杨斐
(安徽省淮北市实验高级中学)
数形结合是当前高中数学教学中常用的方法之一,通过将直观的图形与抽象的数字联系起来,使数学问题更加直观,更加容易理解。通过分析数形结合思想在高中数学教学中的意义,探究在高中数学教学中的应用,促进高中数学教学的发展。
数形结合;高中数学;教学应用
一、数形结合思想在课前学习中的应用
学生在课前要认真完成学习中的预习任务,而教师则对学生课前学习任务进行批阅,从而及时发现并解决学生预习中存在的问题。通过课前学习的“导”帮助学生了解教学的基础内容,能够形成有效的教学认知。因此,课前学习的设计一方面难度不能太大,既要符合学生当前的整体学习水平,又能够逐步引导并激发学生的学习兴趣。另一方面,设计的内容要与课堂教学相呼应,能够为教学活动的开展提供先决条件。在数形结合思想的应用教学课前学习中,教师应该将学生的思维逐渐引向教学方面。
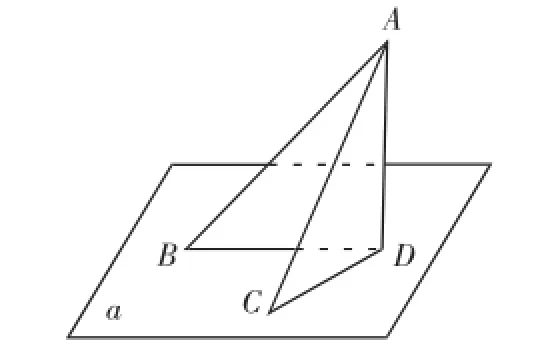
例1.直线与平面垂直的判定(趣味实验导学)
(1)趣味实验
用一张三角形的纸片,在△ABC中过A点作AD⊥BC于点D;沿着直线AD将△ABC纸片翻折成一个二面角;将翻折后的纸片中的边BD,CD放在水平桌面α上面,如下图所示。
(2)实验思考
翻折后的纸片△ABC中,边AD与BD,AD与CD有什么位置关系?AD与水平桌面α有什么位置关系?要保证AD与水平桌面α相互垂直,需要满足什么条件?如果AD垂直于水平桌面α内的两条直线,那么AD与水平桌面α是否垂直?
二、数形结合思想在课堂探究中的应用
例2.如图所示,四棱锥中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD,求证(1)PA⊥BD;(2)若PD=AD,求二面角A-PB-C的余弦值。

分析:题目中的第二问,如果采用常规做法,就需要将二面角对应的平面角找出来,此方法最少需要三条辅助线,这样不仅加大了计算量,同时也浪费了大量时间进行实践。但是通过数形结合,运用向量法建立空间直角坐标系,将几何问题代数化,解题过程将非常简洁,且准确度高。
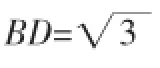
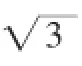
三、数形结合思想在课后反思中的应用
学生在自主学习之后进行反思,通过分析自己的解题方法是否正确,得到的结果是否准确,可以帮助学生发现自己解题思维中的不足,继而找到最有效、最快捷的解题方法,提高自己的解题效率。数学题目规律性、技巧性较强,这就需要学生掌握数学题目的变化规律以及解题思路,能够针对不同的问题采取相应的解题策略。加强对解题方法、技巧的反思,帮助学生理解不同的解题方法,使得学生能够从不同角度去分析、思考、联想某一个数学问题,做到掌握该类型的题目,从而优化学生的解题思路,全面提升学生的思维活跃度。
(1)请给出一组a,b的值,保证直线l和椭圆C相交;
(2)直线l和椭圆C相交的时候,a,b应该满足什么条件;
(3)如a+b=1,试判断直线l和椭圆C自己的位置关系。
【变式1】已知a+b=1,直线l和椭圆C相交于A、B两点,A、B两点关于直线M:y=kx+m对称,试求k、m之间的关系。
【变式2】已知a+b=1,直线l和椭圆C相交于两点A、B,添加一个条件,求出直线l的方程。
[1]李红梅.例谈数形结合在高中数学中的应用[J].新课程研究,2010(5):177-178.
[2]杜路敏.浅析高中数学教学中数形结合思想的运用和实施[J].学周刊,2013(8):141.
·编辑孙玲娟

