摆动式突防对比例导引弹道的影响分析及仿真*
潘乐飞,刘新学,李邦杰,杨 涛,姚占朝( 第二炮兵工程大学,西安 7005; 9667部队,福建永安 66000; 966部队,河南栾川 47500)
摆动式突防对比例导引弹道的影响分析及仿真*
潘乐飞1,刘新学1,李邦杰1,杨涛2,姚占朝3
(1第二炮兵工程大学,西安710025;296167部队,福建永安366000;396263部队,河南栾川471500)
为提高弹道机动的有效性或合理设计拦截制导律,需要定性分析突防弹与拦截弹间的法向过载关系、视线角速度变化规律、拦截弹道的稳定性等问题。对相对运动方程的相关参数进行合理简化后,推导了由于突防弹机动引起的拦截弹比例导引弹道的视线角速度及需用法向加速度的解析公式;在考虑拦截弹制导系统时间延迟时,分析了比例导引弹道的稳定性条件;针对突防弹进行正弦机动的弹道模型,进行了拦截仿真,验证了解析公式的合理性。
弹道机动;比例导引;弹道稳定;正弦机动
0 引言
摆动式机动突防可以最大化拦截弹的末端脱靶量或提前耗尽拦截弹的机动能量,因此可以有效提高突防弹的生存概率。国内外许多专家学者对摆动式突防策略进行了相关研究。Zarchan[1-2]等基于发展导弹防御系统的角度,推导得到了阶跃及正弦机动条件下拦截弹的脱靶量公式,得到了拦截弹脱靶量的均方根;崔静、姜玉宪[3]等从突防效果及工程实现方法等方面研究了摆动式突防策略的有效性;魏鹏鑫[4]等站在攻防双方的立场,研究了攻防双方的机动过载关系;顾文锦[5]等研究了反舰导弹末端机动式不同对突防效果的影响。
文中针对文献[6]的滑翔弹侧向机动模型及典型的比例导引拦截律,分析了突防弹机动与拦截弹视线角速度及需用法向加速度的关系,并考虑拦截弹制导系统时间延迟对拦截过程及终端脱靶量的影响,最后给出了仿真验证。
1 突防弹侧向机动弹道描述
摆动式机动弹道可以有多种形式,文中采用基于正弦规律的机动方法(见图1所示)。以x轴方向的位移为自变量,则侧向机动函数式可表示为:式中:z0为初始值;ω为机动频率;Lz为机动幅值;ω0为初始相位角;x为突防弹当前位置在x轴方向上的分量。


图1 摆动式机动突防示意图
文中令Lz和ω均为常值,令 ω0为0。则由式(1)得侧向机动速度、加速度分别为:

侧向摆动式机动主要是为了提高突防能力,同时需兼顾能量消耗影响,因此机动幅度不可能太大。为此可假设速度矢量偏离xoy平面的角度为小量,则:

式中:v为突防弹速度大小;D为突防弹所受阻力大小。
令突防弹完成侧向摆动式机动的横向过载为nz,综合以上各式得:
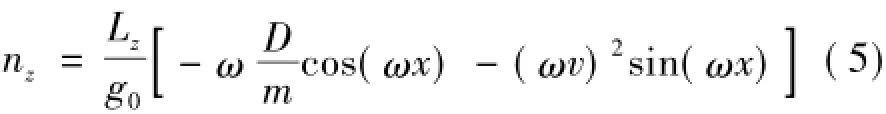
式中g0为海平面处引力加速度。
除给定机动幅度Lz和机动频率ω外,还可采用给定范围内的机动周期数m及一个周期内沿x轴方向的机动距离Ax来描述飞行器机动特性。若机动范围为[0,xf],则有:

2 拦截弹比例导引律分析
2.1比例导引基本公式

或

式中:K、KR是比例系数是导弹和目标的接近速度。
导弹和目标的相对运动关系见图2所示。在惯性坐标系内,可表示为:

式中:R为拦截弹与目标之间的相对距离;λ为目标视线角;下标M、T分别表示拦截弹和突防弹。
2.2目标视线角的通解



图2 比例导引相对关系示意图
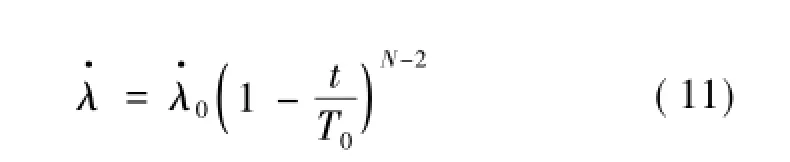
即在有效导航比N>2时,视线角速度是衰减的。且有当t=0时,视线角速度为最大值;当t=T0时,视线角速度为零。也就是说若N>2,在拦截弹与目标遭遇时刻,初始视线角速度误差最终可全部克服。
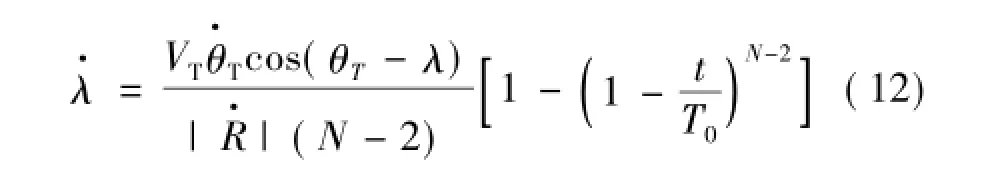
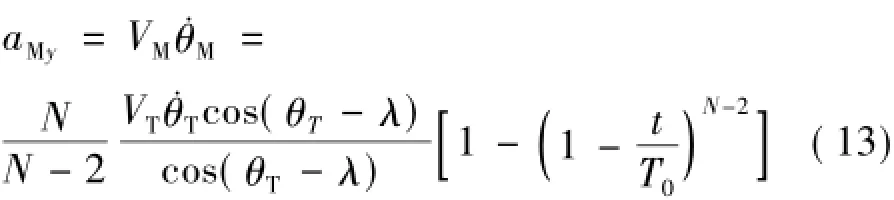
由式(12)和式(13)可知:
2)在一般情况下,拦截弹的需用加速度aMy和突防弹法向加速度
3)拦截弹需用法向加速度aMy的值不仅取决于突防弹法向加速度的大小,而且还与拦截弹、突防弹的相对角位置和有效导航比有关。有效导航比N大时,拦截弹需用法向加速度aMy的最大值可小些。
3.2制导系统动力学特性对导引弹道的影响
3.1节是基于拦截弹制导系统无滞后的理想条件下得到的解析结果,事实上由于导引头及自动驾驶仪的动力学滞后等因素,制导系统必然存在时间延迟。
3.2.1拦截弹系统动力学为无惯性系统
若制导系统为无惯性环节,则控制方程为式(8)。将式(8)代入弹目相对运动方程(9),经整理得特征方程为:
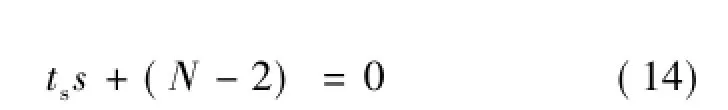
根据古尔维茨稳定性判据可知,由于ts>0,则弹道稳定的充要条件为N-2>0。即当拦截弹系统动力学是无惯性时,只要有效导航比大于2,则比例导引弹道是稳定的。
3.2.2拦截弹动力学等效成一阶惯性系统
比例导引控制方程(8)可改写为:

其中,τ为时间常数。
将控制方程(15)代入相对运动方程(9),并忽略较小的项,可近似得到该条件下的特征方程为:
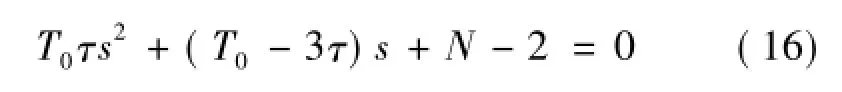
根据古尔维茨稳定性判据,得弹道稳定的充要条件为:

即,导弹制导系统动力学为一阶惯性系统时,比例导引弹道稳定的条件为:
1)有效导航比N大于2。
2)待飞时间T0要大于导弹系统动力学惯性时间常数的3倍。若惯性时间常数τ为0.5 s,则比例导引弹道大约在命中前1.5 s就要开始失稳了。
4 仿真分析
文中基于Matlab Simulation仿真平台,在地面坐标系内建立突防弹与拦截弹的数学模型,对拦截弹的比例导引弹道进行了仿真讨论。
假设拦截弹与突防弹的速度大小为恒值。仿真起始数据为:
3)拦截弹导引方法采用式(15),令 KR=4/ 2 500。
4)目标弹机动方案采用式(1),机动幅值Lz及机动频率ω为恒定值。若令机动周期m=10,则根据式(6)得:

4.1制导系统无时间延迟
令制导方程(15)中的时间常数τ=0。通过仿真,可得以下结论:
1)由图3可知,当假设拦截弹制导系统为理想的无时间延迟环节时,拦截脱靶量可以逼近零值。该结果与式(14)的结论一致,即当不考虑拦截弹制导系统时间延迟时,只要有效导航比大于2,拦截弹导引弹道是稳定的,必然会命中目标。
2)由图3~图5可知,不论是拦截弹的位移、速度还是加速度,其机动频率都与突防弹的频率接近。
3)由图5可知,拦截弹需用法向加速度aMz的幅值由t0时刻开始逐渐增大,至遭遇时刻达到最大;且拦截弹aMz的值一般都小于突防弹的机动加速度aTz,只是在遭遇前的极小时间段内拦截弹aMz值会瞬间增大并超过突防弹。该仿真结果与3.1节的结论1)是一致的,即由于突防弹机动使得拦截弹视线角速度 ˙λ及需用法向加速度值都随时间递增,且在拦截遭遇时刻达到最大值。
4)由图5可知,拦截弹需用法向加速度aMz的正负号与突防弹法向加速度aTz的正负并不一致。这是由于突防弹作侧向正弦摆动式突防而导致θT与λ(见图6)都作了周期性的变化,从而使得(θT-λ)及(θM-λ)也有了周期性变化。即此时不能再假设(θT-λ)及(θM-λ)为常值。因此仿真结果与3.1节的结论2)不再一致。
4.2制导系统为一阶惯性环节
令制导方程(15)的时间常数τ=0.5 s,其它仿真数据同4.1节。通过仿真,可得以下结论:
1)由图3可知,当考虑拦截弹制导系统动力学特性时,最终的拦截脱靶量不再为零,也即必然存在一个非零的稳态脱靶量。
2)由图3~图5可知,不论是拦截弹的位移、速度还是加速度,其机动频率都与突防弹的频率接近,但其相位会滞后于突防弹的机动曲线。

图3 突防弹与拦截弹在oxz平面内的位移

图4 突防弹与拦截弹在oz方向的速度

图5 突防弹与拦截弹在z方向的加速度变化曲线
3)由图5可知,拦截弹需用法向加速度aMz的幅值由t0时刻开始逐渐增大,至遭遇时刻达到最大;拦截弹的需用加速度aMz的值一般都小于突防弹的机动加速度aTz,在接近遭遇时刻的一小段时间内拦截弹aMz会增大并超过突防弹aTz。该特点与不考虑制导系统时间延迟的结论类似。根据式(17)可知,当待飞时间小于3τ=1.5 s时,拦截弹比例导引弹道开始失稳,即aTz开始迅速增大,但弹目距离并未趋近于零。
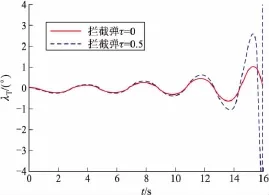
图6 弹目视线方位角变化曲线
5 结论
文中在对突防弹与拦截弹的运动模型进行适当简化后推导并分析了突防弹进行弹道机动时 ˙θT对拦截弹视线角速度 ˙λ及需用法向加速度aMy的解析关系式。采用文献[6]的滑翔弹侧向机动模型对解析关系式进行了仿真验证。仿真结果表明,解析关系式能在一定程度上反映攻防双方参数的变化规律,可以为机动弹道设计及拦截弹制导律设计提供理论参考。
[1]ZARCHAN Paul.Proportional navigation andweaving targets[J].Journal of Guidance Control and Dynamics,1995,18(5):969-974.
[2]YANUSHEVSKY Rafael.Analysis of optimal weaving frequency of maneuvering targets[J].Journal of Spacecraft and Rockets,2004,41(3):477-479.
[3]姜玉宪,崔静.导弹摆动式突防策略的有效性[J].北京航空航天大学学报,2002,28(2):133-136.
[4]魏鹏鑫,荆武兴,高长生.攻防对抗机动过载关系分析[J].宇航学报,2013,34(2):179-185.
[5]顾文锦,赵红超,王凤莲.反舰导弹末端机动的突防效果研究[J].宇航学报,2005,26(6):758-763.
[6]谢愈,刘鲁华,汤国建,等.高超声速滑翔飞行器摆动式机动突防弹道设计[J].航空学报,2011,32(12):2174-2181.
[7]赵善友.防空导弹武器寻的制导控制系统设计[M].北京:中国宇航出版社,2005.
Simulation of Proportional Navigation for Weaving Maneuver Penetration
PAN Lefei1,LIU Xinxue1,LI Bangjie1,YANG Tao2,YAO Zhanchao3
(1The Second Artillery Engineering University,Xi’an 710025,China;2No.96167 Unit,Fujian Yong’an 366000,China;3 No.96263 Unit,Henan Luanchuan 471500,China)
In order to improve maneuver trajectory or design intercept guidance law effectively,qualitative analysis on pursuit and evasion should be launched including the relationship of normal overload,line-of-sight(LOS)angular speed variation trend,and intercept trajectory stability.Based on the simplified engage model,analytic formulas of the LOS angle velocity and the need normal acceleration of the pursuing missile were presented.Considering guidance system time delay,the steady conditions of the proportional navigation trajectory were obtained.The simulation on the lateral sinusoidal maneuver was performed,which proved rationality of the analytic formulas.
maneuver trajectory;proportional navigation;steady condition;sinusoidal maneuver
V448
A
10.15892/j.cnki.djzdxb.2016.01.006
2015-01-05
潘乐飞(1979-),男,河北冀州人,讲师,博士研究生,研究方向:飞行动力学与制导。

