用场协同原理强化换热器传热性能的分析与计算

张 宁（辽宁建筑职业学院，辽宁 辽阳 111000）

用场协同原理强化换热器传热性能的分析与计算

张 宁
（辽宁建筑职业学院，辽宁 辽阳 111000）

以翅片管式换热器的换热性能的提高作为研究重点，通过场协同原理（即在同速度和温度边界条件下，对流换热的性能取决于流体速度场与热流场协同的程度）的运用，以椭圆管来替代圆管来作为将换热器的基管可实现换热器换热性能的提高。经数据测算得，其换热系数有所提升，且阻力系数也发生部分降低。这为强化换热器的热力性能提供了一种较实用的方法。

翅片管式换热器；场协同原理；传热系数；热力计算；对流换热

传热强化技术的采用所带来的各种换热设备的功率及效率提高，及重量和体积的减少，故其在科技界和工业界一直获得高度认可。上世纪出现的世界性能源危机，推动了人们对传热强化技术的探讨和研究。世界各国对其的科学研究的重视，在近二十多年的时间里，形成的与传热强化相关的研究文献不胜枚举［1-3］。在国民生产的各部门中换热器扮演着极其重要的角色，特别在制冷空调应用领域更是翘楚。

从传热的基本公式Q=KF△t可看出，换热量Q的增大可借助与之成正比的传热系数K的提高，传热面积F的扩大及传热温差△t的提高这三个方式来完成［4］。可采取具有针对性的相关技术措施，来提升上述3条基本途径的传热效率的方法主要有5-6］：1）流体的流动情况产生改变；2）流体物性发生改变；3）换热表面情况产生改变。借助粗糙度在传热壁面上的增加，及形状、大小、表面结构于换热面发生相变并在表面增加涂层可促进第3种方法的完成。本文中，作者基于场协同原理并综合运用第3种方法进行了换热器换热性能的强化性针对翅片式管式的专门研究。

1　物理机制及场协同原理在对流强化上的体现

1.1对流强化所体现的物理机制

热传导、热对流和热辐射可以归结为热量传递常运用的3种模式。而翅片管式换热器在运行中，对流换热占主导的同时三种换热形式共同运转作用。能携带热量的流体宏观运动作为对流换热（热对流）的物理机制，形成了热量传递速率上的对流换热高于纯导热。

从另一方面可知，内热源的导热在对流换热本质上是存在的，发挥当量热源作用的即流体的运动。在强度层面，对流换热与当量热源密切相关，流体与壁面温差、流速和流体热物理特性及运输性质在发挥决定作用的同时流体速度矢量与热流矢量的夹角也发挥重要决定作用。速度矢量与热流矢量在流体中处于平行时，即达最大的热源强度，且形成换热的强化大幅度提升；而遵循等温线进行的流体运动，其无贡献于热量的运输，与纯导热模式无异［7］。故实际中存在这种对流换热强度高于纯导热的错误认识。其实热量传递基本的运行方式并不是对流换热，这仅是流体处于运动情况存在的导热问题。纯导热模式若不依靠流动仍可存在，但对流换热的模式若离开导热则无法存在。

1.2场协同原理在对流强化上的体现［7］

当流速和流体物理性质处于既定范畴中，流动当量热源强度主导着边界上的热流（界面上的换热强度），或者Nu数在Re数、Pr数既定中，无因次流动当量热源是决定因素。速度场和热流场本身是流动当量热源中的一个决定因素，同样它们间的夹角也是重要因素，也就是说速度场、热流场、夹角场的绝对值在起决定的同时，相互配合的这3个标量值也起着同等决定作用。速度场与热流场的配合在吐过对路换热中能实现无因次流动当量热源强度的提升，进而促进换热的强化性能，此说明速度场与热流场的较佳协同。速度场与温度梯度场可借助下面三个层面获取协同：

夹角余弦值在速度矢量与温度梯度矢量两者中达到最大限度，即两矢量的夹角β达到最小（β＜90°）或β达到最大（β＞90°）。

最大限度得让流体速度剖面和温度剖面达到均匀（流速最大化和温差既定的状态）。

最大限度让3个标量场（速度绝对值、温度梯度绝对值、夹角余弦值）中的大值与大值相匹配，即要让3个标量场的大值在整个场上的某些域中最大限度呈现。

结合文中信息，场协同原理借助传热强化阐述为：速度和物性于流体中的表现及闭面与流体间的温差在关乎着对流换热的性能同时，协同程度在流体速度场与流体热流场两者间也不容忽视。速度和温度边界处于等同的状态中，其换热强度于协同程度两者成正比。

1.3场协同原理具体应用的表现

基于对流换热中流场与温度场（热流场）的耦合状况，故通过改善场的协同来获取传热性能强化的确艰难异常，若从以下几个层面来尝试，也有达到目的的可能。（1）热边界条件产生变动。 原来的流场不会因热边界条件变动而发生改变，特别是在温度变化对流体的物性影响较小之际。管理Nu的存在差别的原因即等壁温与等热流的充分发展，根由存在于他们的热边界条件相异。若达到一定边界热流，沿流向增加的分布边其换热得以强化；若达到一定温度边界条件，沿流向壁温升高，其传热得以强化。（2）速度分布发生改变 。速度发生的改变势必会带来温度场（热流场）的变动，速度热流矢量的夹角的缩减可借助速度边界条件产生变动来完成，抑或是通过更好配合的3个标量场，以期来实现强化换热。基于管内流动的常规换热，孟继安［8］等借助椭圆界面的放置发生周期性变动，来完成管内流场的改变。（3）具备特殊属性的肋或插入物［9］。与常规情况相异的肋和插入物是参照按照场协同原理而设计而得，它不是为了湍流度和传热面积的增加均不是它的目的。高导热材料构成了纤毛状插入物，正因金属丝相比于管径更细，故有得纤毛状之称。纤毛肋因金属丝与管壁的良好接触而得名，不完全接触即构成纤毛状插入物。管内纤毛丝呈稀松状分布，填充率也只有0.5%～1.0%［8］。

2　传热系数在强化翅片管式换热器上的体现

2.1换热器中所体现的场协同原理

场协同原理在强化的换热器中可理解为：冷热流体温度场间的协同在换热器中与换热性成正比关系［7］。借助两种方式可使得换热器在性能上获得的提升：其一为对流换热系数在流体与壁面间的提升，其中涵盖各种肋片、紊流发生器、插入物等；其二为处于同等的对流换热系数条件，换热器性能的提高借助别的方式，譬如热边界条件的改变等。

此文中阐述的借助场协同原理来实现换热性能的提高即是遵循第二方式，管截面形状产生改变，即翅片管式换热器管截面形状以椭圆形来代替圆形。对于叉流换热器换热性能的提高可借助换热面积的重新布局，来实现温差场均匀性的增高，进而实现冷热流体温度的协同的改善。叉流换热器的效能在换热面积处于最优分布时可获取与同等的逆流换热器的效能，因其本身逆流换热器的换热性较顺流式和叉流式而言更优。

2.2传热系数在矩形翅片椭圆管束换热器中的运算

经实验所得经验公式相对于换热系数而言可表述为

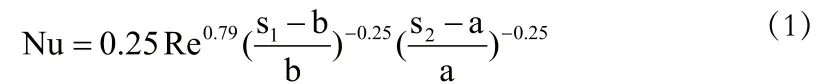
对流动阻力，其准则关系式为

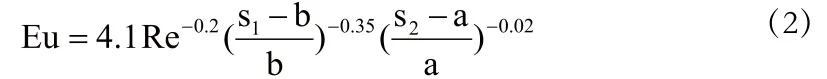
式（1）、（2）中，Nu和Re中的特征尺寸De按下式计算：

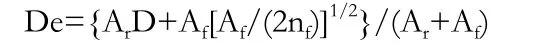
来流的平均温度可作为定性温度，它的应用范畴为：

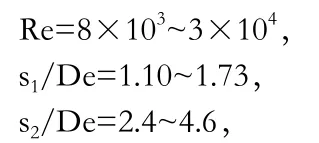
公式里：Ar表示每米管长光管的面积（m2/m）；Af表示每米管长总翅片面积（m2/m）；nf每米管上的翅片数用nf；椭圆管的当量直径（m）用D表示，由下面公式计算其值：

值得表述说明的是：按式（1）计算的管束换热系数可根据翅片管的特征尺寸De计算而得。故需得到整个管束的换热量Q数值时，计算公式（4）应被遵循，即

上述公式中：h表示遵循式（1）算的换热系数（W/m2·℃）；管长（m）用l所示；管子数目用n所示。

表1详细列出了带外翅叉排中椭圆管管束及圆管管束的各项几何参数。从表2可见，换热量比值中可见椭圆管管束较圆管管束而言有了15%的提升，且阻力发生了18%的降低。故处于场协同原理满足的状况中，在基管的选用中以椭圆管束代替圆管管束可达到换热器的传热性能更佳，同时实现其阻力系数的降低。不过问题也随之而生，承压能力小是椭圆管的弊端且制造工艺繁杂，故为防止椭圆形变，管子内外的压力差在椭圆管应用中不宜过高，实际应用中此处应当引起重视。

［1］BERGLES A E. Application of heat transfer augmentation ［M］. New York： Hemisphere Pub， Co. ，1981.

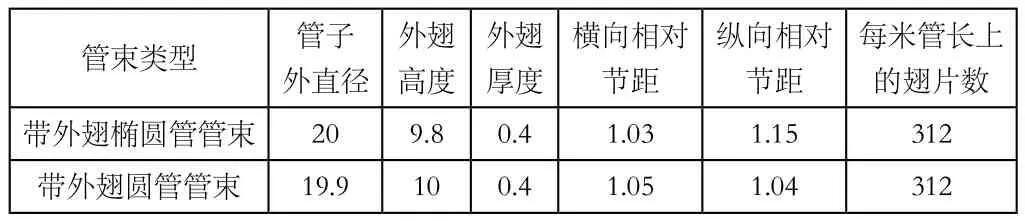
表1　试验管束的几何参数

［2］BERGLES A E. Heat transfer enhancement-Encouragement and accommodation of high heat fluxes ［J］. Journals of heat transfer， 1995， 119：8-19.

［3］WEBB R L. Principle of enhanced heat transfer ［M］. New York：Wiley USA，1994.

［4］史美中，王中铮.热交换器原理与设计［M］.南京：东南大学出版社，2003.

［5］BERGLES A E. Heat transfer Enhancement of heat transfer， a keynote lecture at 6thInt［C］. tronto： Heat Transfer Conf， 1978.

［6］ZUKAUSKAS A. Heat transfer augmentation in single-phase Proc. of 8thInt［C］. San Francisco： Heat Transfer Conf， 1986.

［7］过增元，黄素逸.场协同原理与强化换热新技术［M］. 北京：中国电力出版社，2004.

［8］孟继安，陈泽敏，李志信，过增元.管内对流换热的场协同分析及换热优化［J］.工程热物理学报，2003，24（04）：652-654.

［9］WANG S，GUO Z Y. Heat transfer enhancement by using metallic filament insert in channel flow ［J］.International Journal of Heat Mass Transfer，2001（44）：1373-1378.

表2　叉排椭圆管管束和叉排圆管管束的传热性能及阻力系数的比较

10.16640/j.cnki.37-1222/t.2016.14.054