碱基对在DNA双螺旋链上分离的自由能计算
伍绍贵 冯 丹
(1四川师范大学化学与材料科学学院,成都610068;2中国科学院理论物理研究所,理论物理国家重点实验室,北京100190)
碱基对在DNA双螺旋链上分离的自由能计算
伍绍贵1,2,*冯丹1
(1四川师范大学化学与材料科学学院,成都610068;2中国科学院理论物理研究所,理论物理国家重点实验室,北京100190)
DNA是大部分生物包括病毒的基因载体。DNA双螺旋链通过A=T和G≡C两种碱基对编码实现对遗传信息的存储。碱基对中的相互作用对DNA双螺旋链的稳定性起到重要作用,直接关系到基因的复制和转录。当前研究中,我们构建了四组不同结构的DNA双螺旋链,进行了总共4.3 μs的分子动力学模拟。通过伞形取样技术计算了DNA双螺旋链中碱基对分离的自由能曲线,并从分子尺度细节和相互作用能对自由能曲线进行解析。在碱基对G≡C的自由能曲线(PMF-PGC)上观察到三个峰,通过监测氢键数目的变化发现分别对应于G≡C三个氢键的断裂;而在A=T的自由能曲线(PMF-PAT)上只出现一个峰,说明A=T的两个氢键在分离过程中几乎同时断裂。PMF-PGC的总能垒比PMF-PAT高,主要是因为G≡C比A=T多一个氢键,更稳定。两条曲线的后段自由能仍然升高,而此时碱基对的氢键已断裂,这是DNA链骨架刚性所导致。我们还研究了碱基对稳定性受相邻碱基对的影响,发现邻近G≡C碱基对会增强A=T的稳定性,C≡G会削弱A=T的稳定性,T=A对A=T的影响较小。
平均力势;氢键;分子动力学模拟;伞形取样
1 Introduction
DNA duplexes are double-stranded DNA(dsDNA),in which two complementary nucleic acid strands are combined into one helix.DNA is the primary genetic material for biological objects. The studies on its structures and functions are the basis of exposing biological heredity secrets.Since it was first isolated by the Swiss physician Miescher in 1869,DNA has been extensively studied both experimentally and theoretically1,2.The Nobel Prize in Chemistry 2015 was awarded to three scientists Lindahl, Modrich,and Sancar for their mechanistic studies of DNA repair which provides chemical stability for life.DNA duplexes are coded with two basic components:AT and GC base pairs.AT base pair contains two hydrogen bonds(N6―H62…O4 and N3―H3…O1)as shown in Fig.1(A),so it is referred to asA=T.AGC base pair is more stable than an AT one for one more hydrogen bond (N4―H42…O6,N1―H1…N3,N2―H21…O2),denoted as G≡C here.The interactions between two bases in a base-pair contribute to the stability of DNA duplex,further related to gene replication and transcription.Santalucia has proposed a method to predict the binding free energy for DNA duplex3,which is treated as a string of interactions.However,it cannot intuitively exhibit the details of base pair dissociation and the energetics of this process remains largely unknown.Additionally,it is known to all that G≡C base pair is more stable than A=T base pair. However,when these two base pairs are located in a detailed DNA duplex,due to the rigidity of DNA duplex backbone and the stacking interactions from neighboring base pairs,the free energy difference to separate them is of particular interest.

Fig.1 Molecular structure diagrams for base-pairsA=T(A)and G≡C(B)and four groups of DNAduplexes with different structures (C,D,E,F)studied in this workIn GROUP 1,DNAduplexes consisting of pureA=T base pairs but with different lengths(trimer,pentamer and heptamer)were employed to investigate the influence of DNAchain length on base pair stability.In GROUP 2,DNAheptamers with pureA=T or G≡C base pairs were used to determine the PMFs forA=T and G≡C base pair dissociation.GROUP 3 and GROUP 4 are DNAheptamers with different sequences,which were used to investigate the impact of neighboring base pairs on the stability of A=T or G≡C base pair.These DNAduplexes with different sequences are labeled as PAT,PGC,MAT,MGC,GAG,TAT,and CAC,respectively.
Molecular dynamics(MD)simulation is a powerful auxiliary tool for conventional experiment methods.By using physical force field,MD simulations can mimic detailed interactions among proteins4,5,nucleic acids6,7,lipids8,9,and many small molecules10,11and provide dynamic information to explain many biological phenomena at atomic-level resolution.In this work,we use allatom MD simulations to study the free energy profile and molecular details of base-pair dissociation.The potential of mean force(PMF)profiles for dissociating A=T and G≡C base pairs have been determined.Non-bonded interactions and hydrogen bond number(Nhb)changes during base pair dissociation have been measured to explain these PMF profiles.DNAduplexes with different sequences have been investigated to explore the influential factors on base pair stability.
2 Methods
2.1Model construction
Four groups of DNA duplexes with different compositions and chain lengths were constructed for MD simulations,as shown in Fig.1(C,D,E,F).In GROUP 1,three DNAduplexes with three,five,and seven base pairs consisting of pureA=T base pairs,referred to as trimer,pentamer,and heptamer,respectively,were employed to investigate the influence of chain length on DNA duplex stability.In the second group,two heptamers composed of pureA=TandG≡Csequences,whicharereferredasPATandPGC as shown in Fig.1(D),were employed to elucidate the free energy to dissociate anA=T or a G≡C base pair in DNAduplex.In the third group,the middle base pairs of PATand PGCwere exchanged to yield two mutated heptamers,termed as MGC and MAT respectively,as shown in Fig.1(E).These two mutated heptamers were created to investigate the influence of neighboring base pairs on base pair′s stability.In other words,we calculated the PMFs for anA=T base pair dissociation in a G≡C duplex,and a G≡C base pair dissociation in anA=T duplex.The heptamers in GROUP 4 are all alternating copolymers with middle A=T base pairs,as shown in Fig.1(F),which were employed to verify the influence of neighboring base pairs on base pair′s stability in further.
2.2Simulation details
All simulations were performed using GROMACS software, which is one of the fastest MD simulation packages available12-14. AMBER99SB force field with ParmBSC0 nucleic acid parameters15was used to describe nucleotides in DNAduplex.The DNA duplexes with different sequences in this work were generated using the make-na server(http://structure.usc.edu/make-na/server. html).To create a system of DNAduplex surrounded by explicit water,DNAduplex was initially placed in the center of a cubic box of 5.4 nm×5.4 nm×5.4 nm.The distances from box surfaces to the closest atoms of DNAduplex are at least~1.0 nm,which is safe to prevent DNAduplex from contacting with its periodic images. Next~5000 three-point transferable intermolecular potential (TIP3P)water molecules16were filled to solvate the DNAduplex. Sodium and chloride ions were added to make the solvated system electrically neutral at a concentration of~0.15 mol∙L-1 17,which is close to the physiological ionic concentration.The final system contains~15000 atoms.Atypical 1.0 nm cutoff distance was used for both van der Waals and short-range electrostatic interactions. Long-range electrostatic interactions were treated using the particle-mesh Ewald(PME)summation method18,19.Berendsen barostat20and velocity rescaling thermostat21were applied to control pressure and temperature at 105Pa and 310 K,respectively. Periodic boundary condition was applied in the three dimensions of the simulation box.Motion equations were solved numerically with a time step of 2 fs and the neighbor list was updated every 10 steps.The constructed DNAduplex system was firstly subjected to a thorough energy minimization using steepest descent minimization22followed by a 200 ps MD simulation with position restrains on the heavy atoms of DNA duplex.Thereafter,an equilibrium simulation run was performed at a constant temperature of 310 K and a constant pressure of 105Pa for 1 ns.To generate a representative ensemble of structures,each production simulation was performed for 50 ns and trajectories were saved at 2 ps intervals.The detailed conformation analysis and interaction calculations were conducted using the built-in tools of GROMACS.
2.3Umbrella sampling(US)
US method was used to elucidate the free energy for base-pair dissociation.To carry out US simulation,a series of seed configurations along reaction coordinate should be prepared as initial configurations.The middle base-pairs of these DNA heptamers were chosen for free energy calculation.First each DNAheptamer was solvated and ionized in a water box.After an equilibrium simulation for 1 ns,the resulted structure was used for steered molecular dynamics(SMD)23simulation to create initial seed configurations for US simulations.Here,we chose one base of the middle base pair as the reference point,and the other was applied a pulling force with a force constant k=1000 kJ∙mol-1∙nm-2at a speed of 0.1 nm∙ns-1by SMD simulation.The distance(ζ) between two bases was set as the reaction coordinates for PMF. The SMD simulation produces a set of configurations in the range of ζ≈0.6 to 1.0 nm.To obtain accurate PMF results,40 umbrella windows were used at a spacing of 0.01 nm for each DNA heptamer system.Each umbrella window was simulated for 10 ns under a force constant k=1000 kJ∙mol-1∙nm-2.The first 2 ns simulation trajectory was discarded and the later 8 ns trajectory was sampled at a frequency of every 2 ps for US calculation.The built-in Gromacs tool g_wham24was used to build PMFs along the reaction coordinate ζ.Due to the stacking interactions from neighboring base-pairs and the rigidity of duplex backbone,the obtained PMFs represent free energy profiles for base pair dissociation under the condition close to real environment.
3 Results and discussion
3.1Impact of duplex length on DNA duplex stability
DNA length has significant influence on its stability especially for short DNAchains.To obtain accurate free energy results,largescale simulations should be launched so as to sample conformation space sufficiently.This means that particle systems for US simulations should be as small as possible to save computational resource.Therefore,in current study,it is necessary to choose DNAduplexes with short length,however,which should be stable enough to endure long time simulation without being disintegrated.Thus we firstly investigate the influence of duplex length on its robustness.
For simplicity,DNA duplexes composed of pure A=T basepairs were considered.Three DNAduplexes with 3,5,and 7 basepairs,termed as trimer,pentamer and heptamer,respectively,were generated from make-na server.We performed 10-independent parallel simulations with each DNA duplex and each simulation runs for 50 ns.Hydrogen bond occupancy was used to elucidate the effect of duplex length on the robustness of DNA duplex25. DNA duplexes consisting of pure A=T base-pairs own only two types of hydrogen bonds:N6―H62…O4 and N3―H3…N1.We determined occupancy values for both hydrogen bonds of each base pair for three DNA duplexes,as shown in Fig.2.For hydrogen bond N6―H62…O4,trimer has the weakest stability and pentamer is better,which means that trimer and pentamer cannot endure the thermal disturbance from long time MD simulations.For heptamer,from the 1st base pair to the 3rd one,occupancy value is increasing;the occupancy values for the 4th,5th,and 6th base-pairs are all larger than 0.9,which denotes that these basepairs have established very robust hydrogen bond interactions.For the 7th base-pair(3′terminal),the occupancy decreases to 0.42 sharply.The case for another hydrogen bond,N3―H3…N1,is very similar to that of N6―H62…O:Trimer has the poorest stability;pentamer is better while heptamer has the highest occupancy value in each position as compared to trimer and pentamer.Specially,hydrogen bond N3―H3…N1 has higher occupancy values than N6―H62…O4 in most of the positions except the 3′terminal one.Furthermore,a detailed check of Fig.2 shows that both hydrogen bonds have the highest occupancy values(~0.94 for N6―H62…O4 and~0.99 for N3―H3…N1)in the 4th base-pair of heptamer.Therefore,the middle base pair in heptamer is an idea position for PMF calculation.

Fig.2 Effect of DNAduplex length on base pair stabilityHydrogen bond occupancy is used to characterize the robustness of DNAduplex. Hydrogen bond is assumed to be present when donor-acceptor distance is less than 0.35 nm and hydrogen-donor-acceptor angle is less than 30 degree. Hydrogen bond occupancy is defined as the ratio of times where the hydrogen bond is present with relative to the total time length of simulation trajectory. Here,three DNAduplexes(Trimer,Pentamer,and Heptamer)were employed to study the influences of duplex length on DNAduplex stability.They are all comprised ofA=T base-pairs.We performed 10-independent 50 ns simulations for each DNAduplex and conformations were sampled at every 2 ps. Atotal number of 250000 conformations were taken from 10 trajectories for the hydrogen bond occupancy calculation for each DNAduplex.

Fig.3 Schematic diagrams of US implementation(A)ADNAheptamer(colored in yellow)is cut out from a long DNAduplex(colored in white).The base pair(colored in blue)in the middle position of the heptamer is chosen for US simulations.The harmonic spring for US is applied on the center of masses of two aromatic rings of the chosen base pair.(B)and(C)Definition of reaction coordinates for base pairsA=T and G≡C.The centers of mass of the aromatic rings forA,T,G,and C are highlighted as magenta points. The distances between them are chosen as the reaction coordinates(ζ)for PMF,such as ζATand ζGCfor base-pairsA=T and G≡C,respectively. (D)distance distributions for ζATand ζGCfrom unbiased MD simulations.color online
Subsequently we determined the equilibrium lengths between two aromatic groups inA=T and G≡C base-pairs.For clarity,the centers of mass of the aromatic rings for A,T,G,and C are referred to as COMA,COMT,COMGand COMC.The distances(ζ) between them are chosen as the reaction coordinates for PMF.The distance between COMAand COMTin the 4th base-pair of anA=T heptamer is denoted as ζATas shown in Fig.3(A,B)while the distance between COMGand COMCin the same position of a G≡C heptamer is denoted as ζGCas shown in Fig.3(C).We conducted two unbiased MD simulations with A=T and G≡C heptamers respectively with each one runs for 50 ns.The distance distributions for ζATand ζGCare calculated as shown in Fig.3(D).It is apparent two base pairs have close equilibrium lengths with their values~0.63 nm forA=T and~0.65 nm for G≡C.Since hydrogen bond is considered to be broken at a distance larger than 0.35 nm, the range of reaction coordinate ζ is set as 0.6-1.0 nm in US simulations for bothA=T and G≡C.
3.2Potential of mean force profiles for base-pair
dissociation in DNA duplexes
Firstly we determined the dissociation PMFs forA=T and G≡C in their pure heptamers(PAT and PGC,Fig.1(D)).For clarity, the two profiles are referred to PMF-PAT and PMF-PGC,re-spectively(similarly hereinafter).For each one,at least 400 ns of US simulations were performed.Fig.4(A)displays the obtained free energy profiles.Along the reactive coordinate ζ,two PMFs are increasing and their energy free energy minima are both located at near ζ≈0.64 nm.However,their PMFs are very different in shape.PMF-PGC is significantly higher than PMF-PAT in most of the range.This is because that G≡C base pair has one more hydrogen bond,it is significantly more stable and more energy is needed to separate it.PMF-PAT is relatively simple with only one peak at near ζ≈0.74 nm.The PMF changes are also qualitatively reflected in the evolution of hydrogen bond number(Nhb).As shown in Fig.4(B),Nhb-PAT has a sharp decrease from 2 to 0 in the narrow range ζ≈0.70-0.75 nm,which denotes that two hydrogen bonds of A=T base pair were almost broken within a short time. As a result,only one disruption peak is observed for PMF-PAT. After hydrogen bonds disruption(ζ>0.90 nm),PMFs are still increasing along the reaction coordinate,which is mainly contributed by the rigidity of DNA duplex backbone.On the other hand,PMF-PGC has three disruption peaks(circled by dash lines), located at near ζ≈0.72,0.79,and 0.90 nm,respectively.Fig.4(B) clearly exhibits that the three moments the G≡C base pair loses its three hydrogen bonds.As shown in Fig.4(A),the energy barriers for three peaks are~23,~11,and~5 kJ∙mol-1,respectively. The first peak(near 0.72 nm)is the sharpest because all three hydrogen bonds of the G≡C base pair contribute to it though only one is broken here.In the same way,the remained two hydrogen bonds contribute to the second peak(near 0.79 nm),where only one hydrogen bond is broken as well.The third peak is the weakest for only one base pair contributes it.From above analysis, it is clear that these peaks in PMF profiles correspond to the rupture moments of hydrogen bonds in G≡C base pairs.Therefore,these peaks are termed as hydrogen bond rupture peaks below.

Fig.4 Potential of mean force profiles,number of hydrogen bonds,and non-bonded interaction energies changes during base-pair dissociation(A)comparison of PMF-PAT and PMF-PGC.(B)the number of hydrogen bonds(Nhb)changes in US simulations.The three dash-line circles in both diagrams corresponding to the moments of hydrogen bonds break.The energies to break three hydrogen bonds are~23,~11,and~5 kJ∙mol-1respectively.(C),(D),and(E)are the total non-bonded interaction energy Etotal,the electric interaction energy Eelec,and the vdW interaction energy EvdWbetween two pulling bases changes during US simulation. All calculations were performed using these trajectories from US simulations and subsequently binned to yield the average value at a given ζ.
The difference between PMF-PAT and PMF-PGC can be partly explained by non-bonded interaction energies between two bases during base pair dissociation.Fig.4(C-E)show the non-bonded energies obtained from US trajectories.It is clear that the electric interaction energy Eelecis larger than the vdW interaction energy EvdWin one order of magnitude.As a result,the total non-bonded energy Etotalas shown in Fig.4(C)is more close to Eelecin Fig.4(D) in shape,which suggests that electric interaction plays more dominated roles than vdWinteraction in maintaining DNAduplex′s stability.On the other hand,the Etotalof G≡C base pair is larger than that for A=T base pair in absolute value,which is consistent with their PMF difference.This result is in agreement with the fact that G≡C base pair has better stability than A=T base pair. However,during the base pair dissociation in the distance rangeζ≈0.64-1.00 nm,the Etotalhas a total of~100 kJ∙mol-1decrease in absolute value for G≡C base pair and~50 kJ∙mol-1decrease for A=T base pair,which are significantly different from their PMF variations.It suggests that besides non-bonded interactions, other components have participated in maintaining the stability of DNA duplex,such as the stacking interactions from neighboring base pairs,the backbone rigidity of DNA duplex,etc.Unfortunately,these contributions cannot be evaluated by using current methods.All these components prevent base pair from dissociation and contribute to the stability of DNAduplex together.
Furthermore,it is of interest whether neighboring base pairshave influences on the stability of the chosen one.Therefore,we prepared two mutated DNA duplexes:one is substituting the middle base pair in a PGC heptamer to an A=T one,denoted as MAT;the other is the substitution of the middle base pair in a PAT heptamer to a G≡C one,denoting as MGC.Both mutated heptamers are shown in Fig.1(E).Then we performed US simulations to determine their corresponding PMFs,PMF-MAT,and PMFMGC,as shown in Fig.5(A).For comparison,PMF-PAT and PMFPGC are also plotted.For A=T base pair,PMF-MAT almost overlaps with PMF-PATin the section ζ=0.60-0.73 nmand PMFMAT is higher than PMF-PAT in the section ζ>0.75 nm.Especially,the hydrogen bond rupture peak near ζ≈0.74 nm in PMFMAT is obviously higher than that in PMF-PAT,which suggests that neighboring G≡C base pairs have increased the free energy barrier for base pair dissociation and improved the stability ofA=T base pair.On the other hand,PMF-MGC is lower than PMFPGC in the section ζ=0.70-0.90 nm,which indicates neighboring A=T base pairs decrease the stability of G≡C base pair.The above results suggest that neighboring base pairs have different influences on the stability of the chosen base pair,positively or negatively.
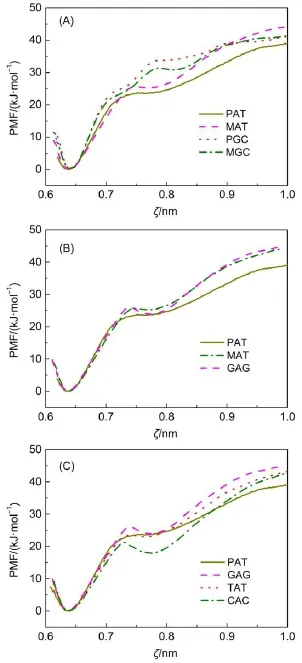
Another important issue is whether alternating sequences are favorable for increasing DNA duplex′s stability.Therefore,we prepared another group of heptamers with alternating sequences. For comparison,their middle base pairs are all set as A=T base pairs,as shown in Fig.1(F).These heptamers are referred to as GAG,TAT,and CAC and their corresponding PMFs are labeled as PMF-GAG,PMF-TAT,and PMF-CAC respectively.Fig.5(B) displays PMF-MAT and PMF-GAG.For comparison,PMF-PAT is also plotted.For heptamers MAT and GAG,the neighboring base pairs of the middle A=T base pairs are all G≡C base pairs while GAG is a heptamer with alternating sequence.As shown in Fig.5(B),their PMF curves almost overlap with each other,indicating that alternating sequence has little impact on DNAduplex stability.In order to further clarify the impact of neighboring base pairs on the stability of middle base pair,Fig.5(C)shows the PMFs for heptamers PAT,GAG,TAT,and CAC.These heptamers have middle A=T base pairs neighboring with different base pairs.It is significant that PMF-PAT is higher than PMF-CAC while lower than PMF-GAG in most of the range,which suggests that neighboring G≡C base pairs enhance A=T base pair′s stability while neighboring C≡G base pairs reduce the stability of A=T base pair.PMF-TAT is very close to PMF-PAT before ζ≈0.82 nm while higher than PMF-PAT at the section ζ>0.82 nm.Since base pair A=T has lost its two hydrogen bonds when the separating distance is larger than ζ≈0.82 nm,the energy difference between PMF-TAT and PMF-PAT is deduced to be attributed by the backbone rigidity of DNAduplex.It means that neighboring T=A base pairs cause little influences on the stability of A=T base pair.On the other hand,these PMFs are still very similar in shape, for instance,only one peak and one valley appearing in the rangeζ≈0.70-0.80 nm.Therefore,we can draw a conclusion that neighboring base pairs do have influences on the stability of middle base pair,but these influences are different,positively or negatively.
4 Conclusions
In this work,we used all-atom MD simulations combined with US method to determine the free energy profiles for base pair dissociation in DNA duplex.Four groups of DNA duplex models have been constructed:the first group is used to examine the effect of chain length on DNAduplex′s stability;the other three groups, which are all heptamers with different sequences,are used for PMF calculations in different DNA duplex sequences.We have launched a total of 4.3 μs MD simulations,in which 2.8 μs were US simulations to obtain accurate PMF profiles for base pair dissociation.The results show that the free energy to split a G≡C base pair is higher than that for an A=T base pair,which is resulted from the fact that G≡C base pair has one more hydrogen bond and it is more stable than A=T base pair.PMF-PGC hasthree peaks,representing the three moments the G≡C base pair loses its three hydrogen bonds,respectively.Differently,PMF-PAT has only one peak,indicating that two hydrogen bonds of theA=T base pair were broken within a very short time.Both PMF-PAT and PMF-PGC are still increasing after their hydrogen bonds were fully broken,which are mainly attributed to the backbone rigidity of DNA duplex.Additionally,non-bonded interaction analysis suggests that electric interaction plays more important roles than vdW interaction in maintaining DNA duplex′s stability.Additionally,we have found that neighboring base pairs do have influences on the stability of the selected base pair.Neighboring G≡C base pairs improveA=T base pair′s stability while neighboring C≡G base pairs reduce the stability of A=T base pair;Neighboring T=A base pairs cause little influences on the stability of A=T base pair.Moreover,alternating sequence has little impact on DNAduplex stability.
The above calculated PMF results may be different from Santalucia′s binding free energy for DNA base pairs.Our PMF curves were calculated from model systems of DNA duplexes in explicit water and the dynamics of particles has been considered. For base pair A=T or G≡C in a detailed environment,the free energy to dissociate them is contributed by not only hydrogen bonds,but also other components,such as the π-π stacking interactions from neighboring base pairs,the rigidity of DNAduplex backbone,and so on.As a result,these free energy results reveal more molecular details and are more meaningful.
Acknowledgments:Thank Prof.WANG Yi in Chinese University of Hong Kong,Prof.SHI Hua-Lin in Institute of Theoretical Physics,Chinese Academy of Sciences,and Prof.JI Qing in Hebei University of Technology for helpful advices.
References
(1)Cressey,D.Nature 2015,526(7573),307.doi:10.1038/ nature.2015.18515
(2)Peyrard,M.;Bishop,A.R.Phys.Rev.Lett.1989,62(23), 2755.doi:10.1103/PhysRevLett.62.2755
(3)Santalucia,J.Proc.Natl.Acad.Sci.U.S.A.1998,95(4), 1460.doi:10.1073/pnas.95.4.1460
(4)Wu,S.G.;Gao,X.T.;Li,Q.;Liao,J.;Xu,C.G.Acta Phys.-Chim.Sin.2015,31(9),1803.[伍绍贵,高晓彤,李权,廖杰,徐成刚.物理化学学报,2015,31(9),1803]. doi:10.3866/PKU.WHXB201508062
(5)Meng,X.M.;Zhang,S.L.;Zhang,Q.G.Acta Phys.-Chim. Sin.2016,32(2),436.[孟现美,张少龙,张庆刚.物理化学学报,2016,32(2),436].doi:10.3866/PKU.WHXB201511302
(6)Silva,D.A.;Weiss,D.R.;Avila,F.P.;Da,L.T.;Levitt,M.; Wang,D.;Huang,X.Proc.Natl.Acad.Sci.U.S.A.2014,111 (21),7665.doi:10.1073/pnas.1315751111
(7)Mackerell,A.D.;Banavali,N.K.J.Comput.Chem.2000,21 (2),105.doi:10.1002/(SICI)1096-987X(20000130)21:2<105:: AID-JCC3>3.0.CO;2-P
(8)Ge,Z.;Li,Q.;Wang,Y.J.Chem.Theory Comput.2014,10 (7),2751.doi:10.1021/ct500194s
(9)Delemotte,L.;Tarek,M.J.Membr.Biol.2012,245(9),531. doi:10.1007/s00232-012-9434-6
(10)Da,L.;Avila,F.P.;Wang,D.;Huang,X.PLoS Comput.Biol. 2013,9(4),e1003020.doi:10.1371/journal.pcbi.1003020
(11)Yang,L.J.;Gao,Y.Q.Acta Phys.-Chim.Sin.2016,32(1), 313.[杨立江,高毅勤.物理化学学报,2016,32(1),313.]
doi:10.3866/PKU.WHXB201512161
(12)Kutzner,C.;Van Der Spoel,D.;Fechner,M.;Lindahl,E.; Schmitt,U.W.;De Groot,B.L.;Grubmüller,H.J.Comput. Chem.2007,28(12),2075.doi:10.1002/jcc.20703
(13)Pronk,S.;Páll,S.;Schulz,R.;Larsson,P.;Bjelkmar,P.; Apostolov,R.;Shirts,M.R.;Smith,J.C.;Kasson,P.M.;van der Spoel,D.Bioinformatics 2013,29(7),845.doi:10.1093/ bioinformatics/btt055
(14)Hess,B.;Kutzner,C.;Van Der Spoel,D.;Lindahl,E.J.Chem. Theory Comput.2008,4(3),435.doi:10.1021/ct700301q
(15)Perez,A.;Marchan,I.;Svozil,D.;Sponer,J.;Cheatham,T.E., III;Laughton,C.A.;Orozco,M.Biophys.J.2007,92(11), 3817.doi:10.1529/biophysj.106.097782
(16)Miyamoto,S.;Kollman,P.A.J.Comput.Chem.1992,13(8), 952.doi:10.1002/jcc.540130805
(17)Ito,H.O.;Soutome,S.M.J.Microbiol.Methods 2003,55(1), 29.doi:10.1016/S0167-7012(03)00111-8
(18)Essmann,U.;Perera,L.;Berkowitz,M.L.;Darden,T.;Lee, H.;Pedersen,L.G.J.Chem.Phys.1995,103(19),8577.
doi:10.1063/1.470117
(19)Darden,T.;York,D.;Pedersen,L.J.Chem.Phys.1993,98 (12),10089.doi:10.1063/1.464397
(20)Berendsen,H.J.;Postma,J.P.M.;van Gunsteren,W.F.; DiNola,A.;Haak,J.J.Chem.Phys.1984,81(8),3684.
doi:10.1063/1.448118
(21)Bussi,G.;Donadio,D.;Parrinello,M.J.Chem.Phys.2007, 126(1),014101.doi:10.1063/1.2408420
(22)Zimmermann,K.J.Comput.Chem.1991,12(3),310.
doi:10.1002/jcc.540120305
(23)Isralewitz,B.;Gao,M.;Schulten,K.Curr.Opin.Struc.Biol. 2001,11,224.doi:10.1016/S0959-440X(00)00194-9
(24)Hub,J.S.;De Groot,B.L.;Van Der Spoel,D.J.Chem. Theory Comput.2010,6(12),3713.doi:10.1021/ct100494z
(25)Huang,X.;Wang,D.;Weiss,D.R.;Bushnell,D.A.;Kornberg, R.D.;Levitt,M.Proc.Natl.Acad.Sci.U.S.A.2010,107 (36),15745.doi:10.1073/pnas.1009898107
Free Energy Calculation for Base Pair Dissociation in a DNA Duplex
WU Shao-Gui1,2,*FENG Dan1
(1College of Chemistry and Material Science,Sichuan Normal University,Chengdu 610068,P.R.China; (2State Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences, Beijing 100190,P.R.China)
DNAis the main genetic material for living organisms including many viruses.DNAduplex,coded with A=T and G≡C base pairs,is well suited for biological information storage.The interactions between two bases in a base pair contribute to the stability of DNA duplex,and are further related to gene replication and transcription.In this study,we use all-atom Molecular dynamics(MD)simulations combined with Umbrella sampling(US)method to determine the free energy profiles and explore the molecular details for base pair dissociations.Four groups of DNAduplexes with different sequences have been constructed and a total of 4.3 μs MD simulations have been carried out.In the potential of mean force(PMF)profile for G≡C base pair dissociation(denoted as PMF-PGC),we observed three peaks,which correspond to the three moments G≡C base pair loses its three hydrogen bonds respectively.Differently,A=T base pair loses its two hydrogen bonds within a very short time.As a result,only one hydrogen bond rupture peak was observed in its PMF curve (denoted as PMF-PAT).Compared with PMF-PAT,the overall free energy barrier in PMF-PGC is higher,which is due to the better stability of G≡C than A=T.In the latter sections of both PMFs,free energies are still increasing,which is mainly resulted from the rigidity of DNA duplex backbone.We have also investigated the impact of neighboring base pairs on the stability of middle one.It is found that neighboring G≡C base pairsincrease the stability ofA=T base pair while neighboring C≡G base pairs reduce the stability ofA=T base pair. Additionally,neighboring T=Abase pairs have little influence on the stability ofA=T base pair.
December 16,2015;Revised:February 16,2016;Published on Web:February 18,2016.
Potential of mean force;Hydrogen bond;Molecular dynamics simulation;Umbrella sampling
O641
10.3866/PKU.WHXB201602185
*Corresponding author.Email:wsgchem@foxmail.com.
The project was supported by the National Natural Science Foundation of China(11405113),Science and Technology Plan of Sichuan Province, China(2010JY0122),and Science Research Fund of Sichuan Normal University,China(10MSL02).
国家自然科学基金(11405113),四川省科技厅项目(2010JY0122)和四川师范大学科学研究基金(10MSL02)资助

