微积分及其在生活中的应用

葛家宝

吉林市广播电视大学，吉林　吉林　132022



微积分及其在生活中的应用

葛家宝*

吉林市广播电视大学，吉林吉林132022

微积分在近代工业、科研等方面发挥着重要作用。特别是微积分的创建为近代数学的发展起到了很大的推动作用，它是近代数学进一步发展和拓展的重要基础。本文从微积分的创建、定义、以及在生活中的应用等方面剖析微积分的起源、内涵与它的重要作用。

微积分；近代数学；应用

一、微积分的早期以及创立

微积分(Calculus)目的在于研究微分、积分等问题的概念以及应用这一知识解决实际问题。微积分的应用主要是在函数与极限方面的应用。主要是将变化的不可直接计算的量微分成可计算的，求出结果再将结果积分起来。积分学，在求体积面积等方面有非常典型的应用。

微积分的创建并非是一时之工，由上文的叙述可知，它建立的基础是很多极限思想的形成。它的极限思想更多得表现在求面积、求体积。尤其是对曲线斜率的求法，它的微分极限思想更是充分得表现。如果把新设的点沿着函数的图象慢慢向那个点逼近,当无限逼近的时候就得到函数图象的切线，这就是微分。

二、微积分的应用

(一)微积分在求不规则体积方面的应用

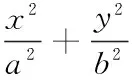
同样，根据第一个类型的思路即可将第二种旋转方式用类似的方法求出。即：

(二)微积分在求平面图形的面积的计算

当f(x)≤0时，由y=f(x)、x=a、x=b与x轴所围成的曲边梯形位于x轴的下方。

牛顿——莱布尼茨公式

运用微积分知识求下列积分：

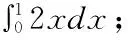
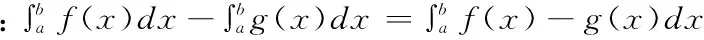
在日常生活中有很多地方要应用到面积计算问题，下面就是几个不规则图形面积计算的相关题目。

3.求曲线方程y=x2以及曲线方程y=2x所围成的区域面积。

解：先求出P点坐标。

∴P点的坐标是(2,4)。

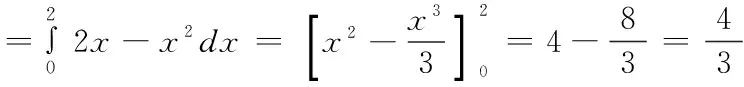
三、总结

微积分在当今生活运用之广泛，使得人们对微积分越来越重视，在各类理工专业的学习上，微积分都是不可缺少的一类工具。不仅如此，微积分的思想在哲学方面的贡献也不容忽视，他对立统一的思想非常契合唯物辩证法的观点。它先微分后积分的方法使得很多不容易计算的问题变得容易解决，很多需要尝试性试探的问题可以直观处理。

[1]马国良. 微积分发展浅议[J]. 云南财贸学院学报, 2000, 2:45-47.

[2]祁卫红,罗彩玲. 微积分学的产生和发展[J]. 山西广播电视大学学报, 2003(02).

[3]马建珍.反例在数学分析中的作用[J].宜宾学院学报，2006，6(12).

葛家宝(1984-)，男，汉族，吉林德惠人，本科，吉林市广播电视大学，讲师，研究方向：高等数学、经济数学基础、微积分初步。

V249

A

1006-0049-(2016)17-0253-01