重力锚水平承载力特性的有限元分析

李怀亮，黄山田，王晓飞，李飒，徐保照（.中海油安装公司，天津　300456；.天津大学建筑工程学院，天津　30007）

重力锚水平承载力特性的有限元分析

李怀亮1，黄山田1，王晓飞1，李飒2，徐保照2
（1.中海油安装公司，天津300456；2.天津大学建筑工程学院，天津300072）

摘要：针对有关规范给出的重力锚水平承载力计算公式，采用有限元法研究了重力锚在水平力作用下的破坏机理，从而得到了在相同的工况条件下，重力锚水平承载力与其底面积有关，底面积小于最佳面积范围时，水平承载力随底面积的增加而增加，超过最佳面积范围时，随底面积的增加而减小；在锚底面积相同的条件下，锚底形状对承载力影响不大，正方形底面稍优于长方形。

关键词：重力锚；承载力；有限元法；底面积

0　引言

我国海域面积广阔，海底土质多样，有黏土、砂土、珊瑚礁、钙质砂以及岩石等，在不同海域进行工程建设时需要慎重选择锚固基础形式以适应不同的土质特点。

重力锚即重块锚，由混凝土块或钢块、碎金属或其他高密度材料制成。设计的提升能力取决于沉没的锚重，由于其结构形式简单，是使用比较早的一种锚固基础形式。有关重力锚的设计计算，早在1982年Taylor R[1]给出了相应的选取原则和设计计算方法。随着各种新型锚的不断出现，重力锚逐渐不再被人们所关注。但近年来，随着海上构筑物形式的多样化，重力锚因其适应范围广，安装简单等特点，又开始进入人们的视野，并被广泛应用于多种结构物。Michael Grant Seibert （2011）[2]为南佛罗里达海洋再生能源体系设计了重力锚泊系统，讨论了在弗罗里达海底600～800 m水下，年代久远的沉积土、欠固结淤泥、以及有砂土的硬层土可选择的锚泊形式。Harris R E等人（2004）[3]为波浪能转换器（WECs）设计锚泊系统，讨论了该体系所遇到的疲劳荷载和磨损及从工程造价和土质适用上探讨了传统的锚泊系统对该体系的适用性，结论是重力锚比较优越。在一些特殊环境，例如热带岛屿或火山环礁起源地，这些地方一般有陡峭山坡，不规则的地形，不定厚度的沉积物，不同的研究者根据结构物和地质条件的特点也选择了重力锚作为其锚泊形式[4-5]。

为了探讨重力锚在钙质砂上的承载机理，本文利用室内试验方法确定钙质砂的物理力学性质，采用有限元方法对重力锚在水平荷载作用下的承载机理进行了分析、探讨，并根据分析结果对目前常用的重力锚设计计算方法进行了评价。

1　钙质砂的物理力学性质

采用室内试验方法对钙质砂的成分进行测试。样本的钙质砂中CaCO3含量都大于95%，钙质砂的重度为19 kN/m3。试验用钙质砂的颗粒级配见图1，采用此级配的钙质砂在不同的相对密实度下进行直剪试验，得到钙质砂内摩擦角随相对密实度变化的关系见图2。根据上述试验结果，选择重力锚的计算参数。

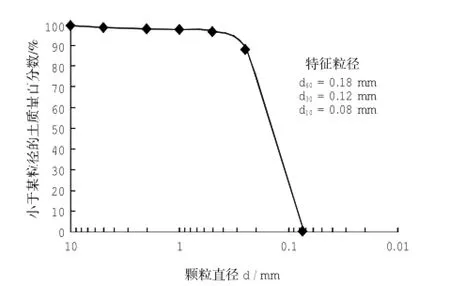
图1　钙质砂的颗粒级配Fig.1　The particle gradation of calcareous sand

图2　钙质砂内摩擦角随相对密实度变化关系Fig.2　The relationship of internal friction angle andrelative density of calcareous sand

2　重力锚的水平承载力

重力锚主要靠自重下锚底与土之间的摩擦力来提供反力[6]。重力锚的外形有多种形式，见图3，工程中比较常用的有（a）、（b）、（d）、（g）。根据工程需要，可以在重力锚的锚底安装剪力键或者裙板，以增加水平承载力，见图4。

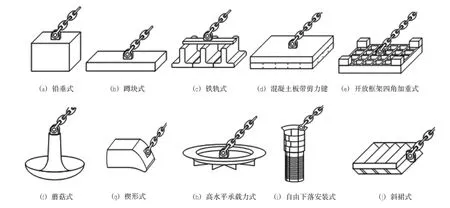
图3　不同形式的重力锚Fig.3　Different shapes of gravity anchor

相关规范[6]给出，对于非黏性土，锚在水平荷载作用下，锚底土体发生排水剪切破坏，其最大水平承载力为：式中：滋为锚底与土体的摩擦系数或为在有剪力键时土与土之间的摩擦系数，在没有剪力键的钢质或混凝土的锚底需要折减5毅），

滋=tan渍（有剪力键的重力锚）；渍为锚底土体内摩擦角；Wb为锚在水下的重力；Fve为设计荷载与锚链荷载竖直方向上的分力（竖直向上为正）；Fh为设计荷载与锚链荷载在水平方向上的分力（沿锚底坡向方向为负）；酌bADf为剪力键间土体的浮重；酌b为土的浮重度；A为锚底面积；Df为剪力键入泥深度，海底泥面以下；β为海底泥面坡角；Rp为锚底前沿的被动土压力，考虑到潮流冲刷等因素，Rp通常被忽略。当β=0且锚链与地面夹角很小可近似看作0时，式（1）可简化为：对于不存在剪力键的情况，将式（2）进一步简化为：也就是说，现有的重力锚分析方法认为，对于不考虑剪力键的重力锚，其水平承载力就是锚底可以提供的摩擦力。

图4　重力锚结构图Fig.4　The structure of gravity anchor

3　重力锚的水平承载机理

3.1有限元模型的建立

为了分析重力锚的水平承载机理，采用有限元方法对承受水平拉力的重力锚进行分析。计算采用ABAQUS软件，单元类型采用C3D8R单元，土体尺寸为20 m伊20 m伊8 m。为了提高模拟精度，土体单元采用渐进加密的单元划分。重力锚的材质为钢材，利用弹性本构对其进行模拟，其密度为7 850 kg/m3，弹性模量取2.1伊105MPa，泊松比0.3。土体采用M-C模型，土重度取19 kN/m3，内摩擦角取35毅，相当于密实钙质砂的内摩擦角，弹性模量30 MPa，泊松比0.25。

本次计算中重力锚不安装剪力键，即重力锚底部为平底。重力锚与土体之间设置接触面，接触面采用surface-to-surface类型，在接触属性定义切向和法向接触面特性，对于切向特性，平底锚采用土体内摩擦角折减5毅取正切；对于法向特性，采用硬接触。土体底部采用双向约束，侧面采用竖向约束。土体的计算范围根据锚体的尺寸确定，计算深度与计算宽度均取为约5B（B为重力锚宽度）以消除边界的影响。在计算分析过程中，均考虑重力锚应用于悬链线式系泊系统，即重力锚只承受水平荷载，Fve=0，海底地面平坦，即β=0。

3.2有限元计算结果与分析

根据计算公式（3）可以看到，重力锚的重量是决定其水平承载力的重要因素，本次计算过程中保持重力锚的重量不变，取为水上重量85 t。在相同的重量下，选取不同的尺度计算重力锚的水平承载力。

图5为重量相同的重力锚在底面积不同时的土体中最大主应变分布图。土体中主应变的分布揭示了土体的滑动情况。

图5　锚底土体破坏时主应变图Fig.5　The principal strain of soil failure under gravityanchor

从图5可以看出，当重力锚底面积较大时，土体中发生变形的土体深度较小，而底面积较小时，发生变形的土体深度较大。图6给出了不同锚底面积水平反力与位移的关系，从图中可以看到在相同的水平位移下，底面积较大的重力锚可以提供更大的反力，也就是其水平承载力较大。

根据上面的计算可以看到，重力锚的底面积大小对重力锚的水平承载力有明显的影响。在重力锚重量相同（Wb一定），土质条件相同（滋也相同），重力锚的水平承载力并不相同。现有的重力锚水平承载力计算公式无法准确反映重力锚的水平承载能力特性。

造成这一现象的主要原因是，在重力锚承受水平拉力发生滑动的过程中，其滑动面并不一定位于重力锚与土体的接触面上，而是可能发生在土体内部，滑动面的深度与重力锚的宽度有关。在抵抗重力锚滑动的过程中，接触面积和滑动深度将同时影响重力锚的水平承载力。接触面积越大，滑动面深度越深，重力锚的水平承载力也就越大。因此，对于重量一定的重力锚存在一个最优面积，使得重力锚的水平抗滑能力达到最大。

采用有限元法对重量为85 t的重力锚选择不同的锚底面积进行计算，重力锚水平承载力随底面积的变化见图7。

图6　不同锚底面积时位移-荷载关系曲线Fig.6　The relationship of displacement-loading withdifferent anchor bottom areas

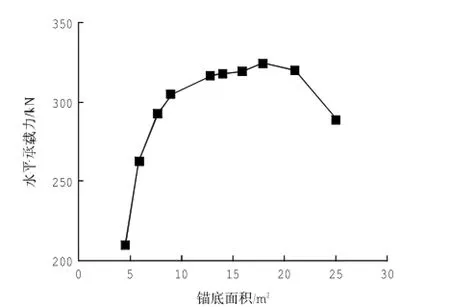
图7 水平承载力随底面积变化Fig.7　The change of horizontal bearing capacity withanchor bottom area

从图7中可以看出，在底面积9～21 m2的范围内，重力锚的水平承载力相差不大，可认为这一范围是重力锚底面积的最佳范围。在小于最佳面积时，承载力随底面积增加而增大，超过最佳面积之后，随底面积增大而减小。

为了研究底面形状对水平承载的影响，选取17.978 m2的底面积，采用长方形和正方形底面进行计算，计算结果见表1。

表1　不同底面形状时的承载力Table 1　The bear capacities of different cross-section shapes

从表1可以看出，锚底形状对水平承载力影响不大，正方形底面对应的承载力稍高于长方形。

4　结语

1）在重力锚承受水平拉力发生滑动的过程中，其滑动面并不一定位于重力锚与土体的接触面上，而是可能发生在土体的内部，滑动面的深度与重力锚的宽度有关。现有的计算重力锚的水平承载力公式无法全面反映重力锚的水平承载力特性。

2）在重力锚重量相同的情况下，其水平承载力与底面积有关。重力锚的底面积存在一个最佳范围，底面积小于最佳范围时，水平承载力随底面积的增加而增加；超过最佳面积时，随底面积的增加而减小；在锚底面积相同的条件下，锚底形状对承载力影响不大，正方形底面稍优于长方形底面。

3）上述重力锚的承载特性在评价重力锚的水平抗滑能力时，需要予以适当考虑。

参考文献：

[1]TAYLOR R J.Interaction of anchors with soil and anchor design [R].California：Naval Civil Engineering Lab,1982.

[2]SEIBERT Michael Grant.Determining anchoring systems for ma原rine renewable energy devices moored in a western boundary cur原rent[D].Florida:The College of Engineering and Computer Sci原ence,Atlantic University,2011.

[3]HARRIS Robert E,JOHANNING Lars,WOLFRAM Julian.Moor原ing systems for wave energy converters:A review of design issues and choices[J].Journal of Engineering for the Maritime Environ原ment,2006,22(12):159-174，

[4]UPSALL Ben,HORVITZ Garry,RILEY Bob,et al.Geotechnical design:Deep water pontoon mooring anchors[C]//Proceedings ports 2013:Successthroughdiversification.USA:ASCE,2013:1087-1096.

[5]TAYLOR R,TRUE D,AMOLD F.Anchoring and mooring consid原erations for an OTEC pilot plant[C]//OCEANS忆10,2010.Sydney: IEEE,2010:1-8.

[6]BARTHOLOMEW Charles A.US navy salvage engineer's hand原book[M].USA:US Navy,1992:G1-G36.

E-mail：lihl@mail.cooec.com.cn

中图分类号：U653.2

文献标志码：A

文章编号：2095-7874（2016）01-0006-04

doi：10.7640/zggwjs201601002

收稿日期：2015-07-23修回日期：2015-11-05

基金项目：国家973项目（2014CB046800）；国家重大专项（2011ZX05056-002-01）

作者简介：李怀亮（1975— ），男，硕士，高工，副总工程师，主要从事海上构筑物的建造、运输、安装等工作。

Finite element analysis on horizontal bear capacity characteristic of gravity anchor

LI Huai-liang1,HUANG Shan-tian1,WANG Xiao-fei1,LI Sa2,XU Bao-zhao2
（1.The Installation Branch of Offshore Oil Engineering Co.,Ltd.,Tianjin 300456,China;
2.Department of Civil Engineering,Tianjin University,Tianjin 300072,China）

Abstract：According to the calculation formula of horizontal bearing capacity of gravity anchor given by relevant specifications,the FEM is used to study the failure mechanism of horizontal bearing capacity of gravity anchor.The results show that under the same working condition,the horizontal bear capacity of gravity anchor relates to its bottom area,it increases with its bottom area increasing before arriving best cross-sectional area and decreases when pass best cross-sectional area.When the same bottom area,the shape of bottom section does not influence on the bearing capacity obviously,and the square section is a bit better than rectangle.

Key words：gravity anchor;bear capacity;finite element method;bottom area