一类β级的α+iv型λ-Bazilerch函数的Fekete-Szegö不等式
鲍春梅
(赤峰学院数学与统计学院,内蒙古赤峰024000)
●数理研究
一类β级的α+iv型λ-Bazilerch函数的Fekete-Szegö不等式
鲍春梅
(赤峰学院数学与统计学院,内蒙古赤峰024000)
引入了一类β级的α+iv型λ-Bazilevich函数A(λ,α,μ,β),并讨论了其子类A(λ,α,0,β)的Fekete-Szegö问题,得到准确结果.
解析函数;β级的α+iv型λ-Bazilevich函数;Fekete-Szegö不等式
设S表示在单位圆E={z:|z|<1}内单叶解析函数f(z)=z+构成的函数类.S*,C和K分别表示通常的星像函数类,凸像函数类和近于凸函数类,它们都是S的子类.
设f(z)与g(z)在E内解析,若存在E内满足|w(z)|≤|z|的解析函数w(z)(不必单叶),使得f(z)=g(w(z)),则称f(z)从属于g (z),记为f(z)≺g(z).
定义设0≤λ≤1,α≥0,v∈R,0≤β<1,若存在g(z)∈S*,使得f(s)∈S,且满足条件

则称f(z)∈S为β级的α+iv型λ-Bazilevich函数,记为A(λ,α,v,β),其中的幂函数取主值.
下面将对函数类A(λ,α,v,β)的子类A(λ,α,0,β)中建立Fekete-Szegö不等式,为此需要如下2个引理:
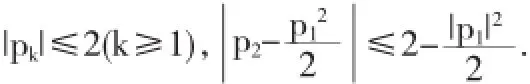
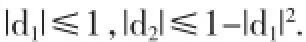
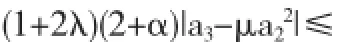

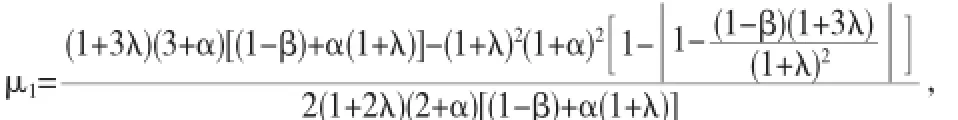
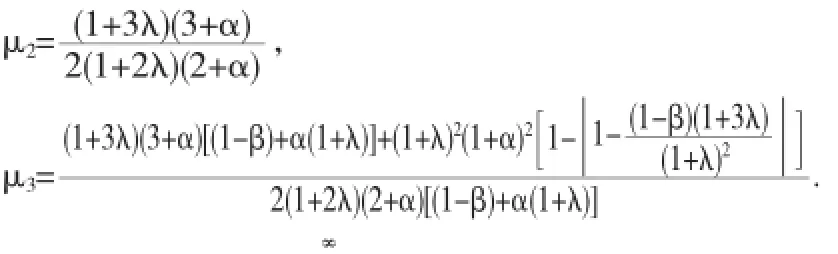
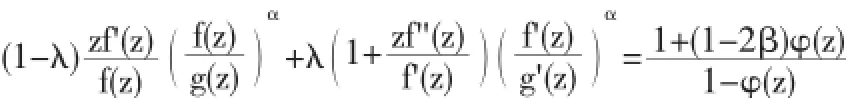
证明因为
将f(z),g(z)和φ(z)的幂级数展开式代入上式,经过一些运算可得
由于g(z)∈S*,所以存在E内具有正实部的解析函数p,使得zg'(z)=g(z)p(z),比较系数可得b2=p1,
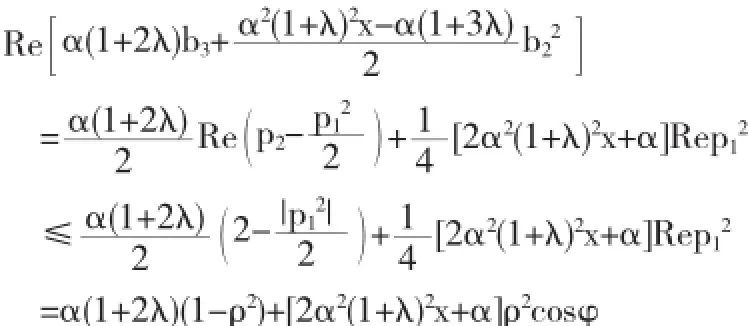
其中b2=p1=2ρeiθ,0≤ρ≤1.
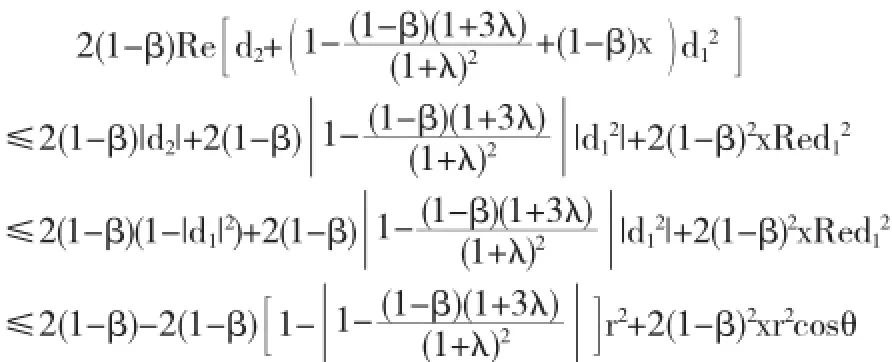
其中d1=reiθ,0≤r≤1,
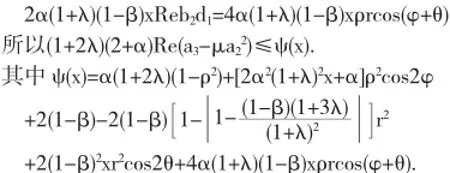
下面分4情况进行证明:

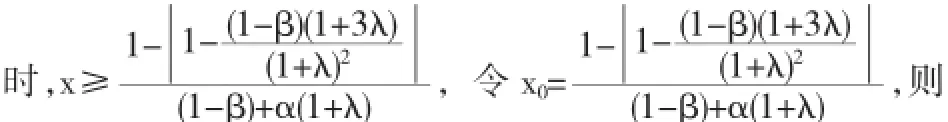
由1)可得
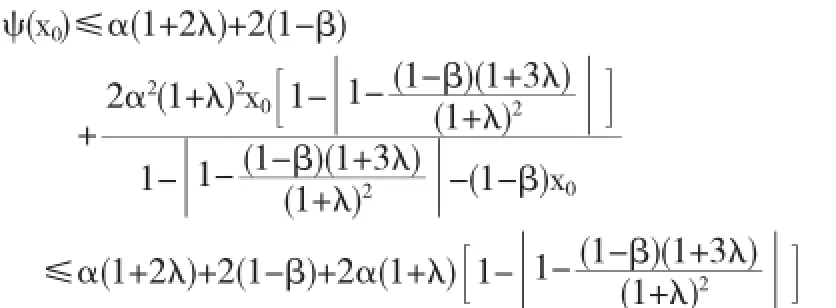
所以ψ(x)=ψ(x0),则通过一些计算可得
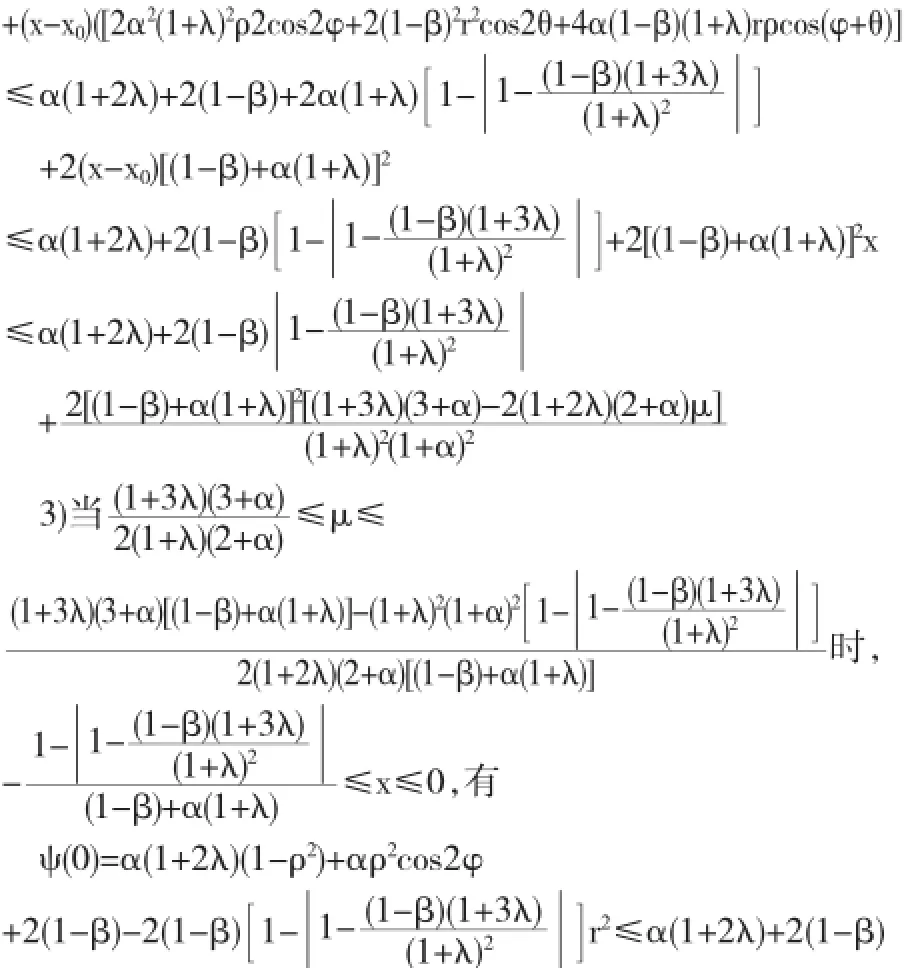
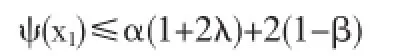
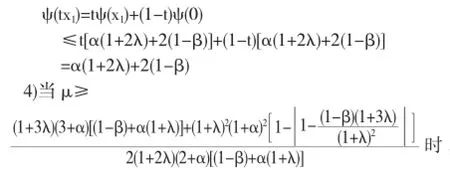
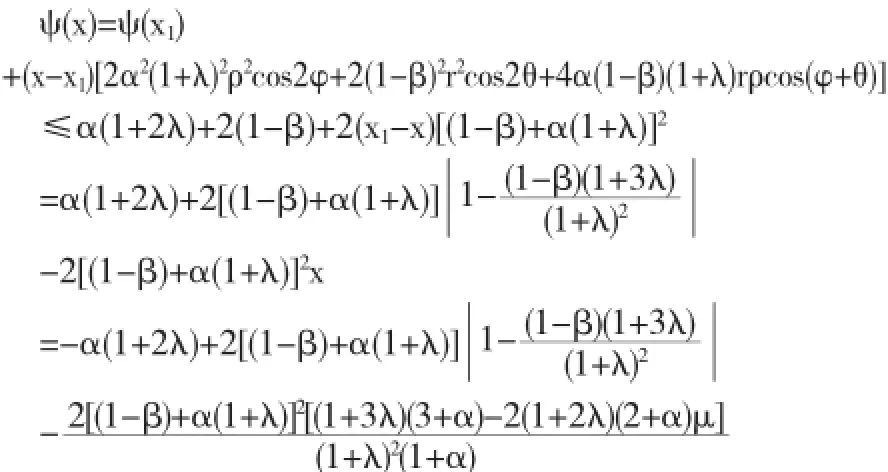
综上所述,本定理得证.
〔1〕刘名生.强拟星函数的Fekete-Szegö不等式[J].数学研究与评论,2000,18(1):99-104.
〔2〕鲍春梅,李书海.一类β级扩展的Bazilevic函数及其Fekete-Szegö问题[J].华南师范大学学报(自然科学版),2010(3):7-10.
〔3〕夏道明,张开明.从属函数的一些不等式[J].数学学报,1958,8(3):408-412.
〔4〕泊茂仁克Ch.单叶函数[M].杨维奇,译.北京:科学出版社,1987.
O174
A
1673-260X(2016)03-0001-02
2015-12-03

