非均匀张力作用下运动薄膜的稳定性研究

王　砚，聂子恒，武吉梅，陈　媛，景　涛，郭旭侠

(1.西安理工大学 土木建筑工程学院，陕西 西安 710048；2.西安理工大学 印刷包装与数字媒体学院，陕西 西安 710048；3.宝鸡文理学院 机械工程学院，陕西 宝鸡 721016)



非均匀张力作用下运动薄膜的稳定性研究

王砚1，聂子恒2，武吉梅2，陈媛2，景涛2，郭旭侠3

(1.西安理工大学 土木建筑工程学院，陕西 西安 710048；2.西安理工大学 印刷包装与数字媒体学院，陕西 西安 710048；3.宝鸡文理学院 机械工程学院，陕西 宝鸡 721016)

文章研究了非均匀张力作用下运动薄膜的动力特性及其稳定性问题。以轴向运动薄膜为模型，建立非均匀张力作用下运动薄膜的计算模型，推导运动薄膜在面内非均匀张力作用下的运动微分方程，采用微分求积法，建立运动系统的复特征值方程。通过数值求解，得到了系统复频率的实部与薄膜长宽比、速度及张力变化系数的关系曲线，并分析了张力变化系数、长宽比和运动速度等参数对薄膜动力特性及稳定性的影响。

非均匀张力；运动薄膜；稳定性

生产中的印刷纸带、印刷薄膜、纺织纤维布匹等均可模化为轴向运动的薄膜，其横向振动使系统产生了不稳定性，限制了它们的应用效果。轴向运动系统其控制方程包含了时间和空间的混合偏导数项，属于经典的陀螺连续体，运动微分方程中包含着丰富的动力学内容。文献[1]阐述了张力控制的基本原理，研究了影响张力波动的因素。文献[2]提出一套保持薄膜所受张力恒定的张力系统补偿策略。文献[3]建立了张力控制系统的数学模型，搭建了系统实验平台并开发出相应算法，在系统实验平台上进行性能实验，对系统算法进行了验证并对系统做出整体分析与评价。文献[4-7]研究了运动薄膜相关参数变化对系统不稳定区域的影响。文献[8-10]基于粘弹性本构研究了黏弹性地基梁横向振动和轴向运动黏弹性梁非线性受迫振动。文献[11]研究了轴向运动薄膜的动态特性和不稳定性。文献[12-13]对轴向运动薄膜的稳定性及横向振动进行控制研究。文献[14]考虑到微小横振动中的张力不相等，将张力角的增量和角度的比值取为变量，提出了一种新方法用以对弦振动和薄膜振动方程进行修正。

目前对于该方面的研究主要集中在均匀张力作用下的轴向运动薄膜，而较少讨论非均匀张力作用下轴向运动薄膜的工作状态及稳定性。但是，实际工作条件下，高速印刷运动薄膜在传输制备过程中由于相邻导纸辊等支撑副的平行度安装加工误差及薄膜运动过程中产生漂移皱褶等因素，易出现张力不均匀性的问题。而印刷机张力控制直接影响着印刷套准精度，张力的微小变化都会严重影响印刷机的印刷质量及工作平稳性。因此必须考虑在非均匀张力作用下，系统会产生的动力学行为。

本文以在非均匀张力作用下轴向运动的承印物为研究对象。研究非均匀张力作用下运动薄膜的稳定性，建立非均匀张力作用下的运动薄膜的计算模型，推导运动薄膜在面内非均匀作用下的运动微分方程，基于微分求积法，建立非均匀张力下运动系统的复特征方程，通过数值求解，分析薄膜几何参数、速度和张力的变化对运动薄膜稳定性的影响。

1　振动微分方程的建立

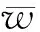
(1)

图1　非均匀张力作用下的印刷运动薄膜Fig.1　The printing moving membrane under the non-uniform tension

若不考虑横向外力，根据达朗贝尔原理，运动薄膜的横向自由振动微分方程为：

(2)

将式(1)带入式(2)，得到非均匀张力作用下运动薄膜的横向自由振动微分方程(3):

(3)

引入无量纲量：

(4)

则方程(3)可化为无量纲形式：

(5)

设方程(5)的解为：

(6)

将式(6)代入式(5)中，得到运动薄膜的横向振动微分方程(7)：

(7)

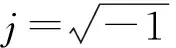
考虑对边固支对边自由边界条件，其无量纲形式为：

(8)

2　复特征值方程的建立

用微分求积法建立非均匀张力作用下运动薄膜的复特征值方程。节点分布方式选用非均匀分布，其中x方向上节点数取Nx，y方向上节点数取Ny，x方向和y方向上取等量的节点数，即Nx=Ny=N。用微分求积法对方程(7)进行离散可得：

(9)

边界条件的微分求积形式为：

(10)

方程(9)和边界条件(10)可写成矩阵形式：

(11)

式(11)构成了系统广义特征值问题，即非均匀张力作用下运动薄膜的复特征值方程为：

(12)

式中，R为广义质量矩阵，G为广义阻尼矩阵，K为广义刚度矩阵，其中包含有薄膜运动速度c、薄膜的张力变化系数β、张力比λ和薄膜的长宽比μ等参数。取不同的参数，可以得到不同复频率的变化关系。

3　数值计算结果及分析

当β=0，c=0和λ=1时，非均匀作用力的运动薄膜的振动方程(9)退化为矩形薄膜无阻尼横向自由振动的振型微分方程。

为了体现微分求积方法是可行有效的，取β=0，c=0，λ=1，不同长宽比μ时，对运动薄膜的前3阶无量纲振动频率计算，并和经典文献[15]的解进行比较，比较的结果如表1所示。从表1可知，本文计算方法(微分求积法)得到的频率和经典文献[15]的解析解相一致，说明应用微分求积法求解运动薄膜的横向振动问题是可行有效的。

表1　振动频率本文解与文献[15]解的比较

图2所示为张力变化系数分别为β=0、β=0.4(λ=1，μ=2)时，无量纲复频率实部与无量纲速度关系曲线。

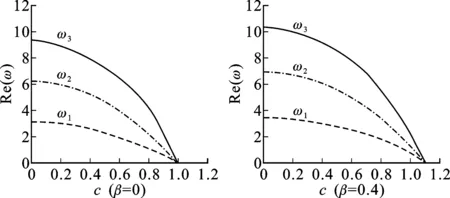
图2　无量纲复频率实部与速度的变化关系 (λ=1，μ=2)Fig.2　The relationship between the real part of dimensionless complex frequencies and velocity (λ=1,μ=2)

从图2可以看出，对于薄膜稳定工作区域(0≤c≤1)的任一速度，张力变化系数越大，薄膜的前三阶无量纲复频率实部值也越大；随着张力变化系数的增大，薄膜失稳的临界速度也逐渐增大，当β=0.4时，临界速度增大到1.17。

图3给出了长宽比μ=2、张力比λ=1时，前三阶无量纲复频率实部同张力变化系数的关系曲线。由图3可知，随着张力变化系数的增大，前三阶复频率实部都呈逐渐增大趋势；对任意相同的张力变化系数，阶数越高，复频率实部则越大。

图3　复频率实部与张力变化系数变化关系 (λ=1，μ=2)Fig.3　The relationship between the real part of complex frequencies and tension coefficient (λ=1,μ=2)

图4给出了张力比λ=1、张力变化系数β=0.5时，无量纲复频率实部与薄膜长宽比的关系曲线。从图中可以看出，第一阶复频率实部的值受长宽比的影响甚小；而第二、三阶复频率实部则明显受到影响，即长宽比越大，第二、三阶复频率实部也会越大。

图4　复频率实部与长宽比的关系 (λ=1，β=0.5)Fig.4　The relationship between real part of complex frequencies and the aspect ratio (λ=1,β=0.5)

图5给出了在长宽比μ=1、张力比λ=1时，运动薄膜临界速度与张力变化系数的关系曲线。从图中可以看出，随着张力变化系数的增大，临界速度的值逐渐增大。

图5　临界速度与张力变化系数的关系 (μ=1，λ=1)Fig.5　The relationship between tension coefficient and critical velocity (μ=1，λ=1)

4　结　论

本文应用微分求积法分析了对边固支对边自由的边界条件下印刷运动薄膜在非均匀张力作用下的振动特性，张力变化对运动薄膜的振动频率和临界速度都有着明显的影响。

1)通过数值求解，得到了系统的复频率的实部与张力变化系数、长宽比及运动速度的变化关系曲线。

2)分析了张力变化系数、长宽比对运动薄膜复频率的影响，研究了张力变化系数对运动薄膜的振动频率及失稳临界速度的影响。

3)得到了张力变化系数与临界速度的关系曲线。

[1]吴俊.冷轧机张力控制系统分析[J].科技与创新,2015(2):9-10.

WU Jun.Cold rolling mill tension control system analysis[J].Science and Technology & Innovation,2015(2):9-10.

[2]张文庆,王凡.薄膜收卷张力控制动力学分析[J].科技视界,2014(28):60-61.

ZHANG Wenqing,WANG Fan.The dynamic analysis on the rolling thin film tension control system[J].Science & Technology Vision,2014(28):60-61.

[3]穆明,曹少中.基于运动控制器的卷筒纸印刷机张力控制系统研究[J].中国印刷与包装研究,2014,6(3):44-51.

MU Ming,CAO Shaozhong.Research on tension control system of web press based on motion controller[J].China Printing and Packaging Study,2014,6(3):44-51.

[4]WU Jimei,LEI Wenjiao,WU Qiumin,et al.Transverse vibration characteristics and stability of a moving membrane with elastic supports[J].Journal of Low Frequency Noise,Vibration and Active Control,2014,33(1):65-78.

[5]WANG Yan,CAO Xiaoshan,JING Tao,et al.Dynamic characteristics and stability of axially moving viscoelastic plate with piezoelectric layer[J].Journal of Low Frequncy Noise,Vibration and Active Control,2014,33 (3):341-356.

[6]WU Jimei,WU Qiumin,MA Li’e,et al.Parameter vibration and dynamic stability of the printing paper web with variable speed[J].Journal of Low Frequency Noise,Vibration and Active Control,2010,29(4):281-291.

[7]武吉梅,王忠民,武秋敏,等.基于微分求积法的变密度印刷纸带振动特性分析[J].振动与冲击，2010,29(3):100-102.

WU Jimei,WANG Zhongmin,WU Qiumin,et al.Analysis of vibration characteristics of printing paper web with variable density based on differential quadrature method[J].Journal of Vibration and Shock,2010,29(3):100-102.

[8]彭丽,丁虎,陈立群.黏弹性三参数地基梁横向自由振动[J].振动与冲击,2014,33(1):101-105.

PENG Li,DING Hu,CHEN Liqun.Transverse free vibration of a beam resting on a three-parameter viscoelastic foundation[J].Journal of Vibration and Shock,2014,33(1):101-105.

[9]唐有绮,陈立群.面内平动黏弹性板非线性振动的内-外联合共振[J].应用数学和力学，2013,34(5):480-487.

TANG Youqi,CHEN Liqun.Internal-external combination resonance of nonlinear vibration of in-plane translating viscoelastic plates[J].Applied Mathematics and Mechanics,2013,34(5):480-487.

[10]丁虎，陈力群.轴向运动黏弹性梁横向非线性受迫振动[J].振动与冲击，2009，28(12)：128-131.

DING Hu,CHEN Liqun.Transverse non-linear forced vibration of axially moving viscoelastic beam[J].Journal of Vibration and Shock,2009,28(12):128-131.

[11]BANICHUK N,JERONEN J,NEITTAANM

KI P,et al.Theoretical study on travelling web dynamics and instability under non-homogeneous tension[J].International Journal of Mechanical Sciences,2013,66:132-140.

[12]NGUYEN Q C,HONG K S.Transverse vibration control of axially moving membranes by regulation of axial velocity[J].IEEE Transactions on Control Systems Technology,2012,20(4):1124-1131.

[13]NGUYEN Q C,HONG K S.Stabilization of an axially moving web via regulation of axial velocity[J].Journal of Sound and Vibration,2011,330(20):4676-4688.

[14]孙逊,张仁杰.对弦振动方程与薄膜振动方程的探讨[J].数学的实践与认识，2010，40(17):236-240.

SUN Xun,ZHANG Renjie.Study on vibrating string equation and vibrating thin film equation[J].Mathematicals in Prictice and Theory,2010,40(17):236-240.

[15]TIMOSHENKO S P,YOUNG D H,WEAVER W Jr,et al.Vibration problems in engineering[M].New York:John Wiley &Sons,Inc,1974.

(责任编辑王卫勋，王绪迪)

The study of stability of the moving membrane under non-uniform tension

WANG Yan1，NIE Ziheng2，WU Jimei2，CHEN Yuan2，JING Tao2，GUO Xuxia3

(1.School of Civil Engineering and Architecture,Xi’an University of Technology,Xi’an 710048,China; 2.Schoolof Printing,Packaging Engineering and Digital Media Technology,Xi’an University of Technology,Xi’an 710048,China; 3.School of Mechanical Engineering,Baoji University of Arts and Sciences,Baoji 721016,China)

The dynamic characteristics and stability of the moving membrane under non-uniform tension are studied in this paper.The axially moving membrane is taken as a model.The calculation model of the moving membrane under non-uniform tension is established.The motion differential equation of the membrance under inhomogeneous tension is derived,and the complex special value equation in motion system is established using differential quadrature method.The relation curves of the aspect ratio,speed and tension variation coefficient of the real part and membrane of the complex frequencies in the system can be obtained through numerical calculation.The effects of the tension variation coefficient,the aspect ratio and the speed on the dynamic characteristics of the membrane are analyzed.

non-uniform tension; moving membrane; stability

10.19322/j.cnki.issn.1006-4710.2016.01.011

2015-04-11

国家自然科学基金资助项目(11272253，11202159，11302003)

王砚，女，副教授，博士,研究方向为机械结构动力学及其稳定性控制。E-mail：wy751112@xaut.edu.cn

O321

A

1006-4710(2016)01-0058-05