基于灵敏度数的薄板结构加强筋布局优化设计
李 蕾 张 葆 李全超 谭淞年
1.中国科学院长春光学精密机械与物理研究所 中国科学院航空光学成像与测量重点实验室,长春,1300332.中国科学院大学,北京,100049
基于灵敏度数的薄板结构加强筋布局优化设计
李蕾1,2张葆1李全超1谭淞年1
1.中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室,长春,1300332.中国科学院大学,北京,100049
提出了一种启发式的加强筋生长设计方法,加强筋从给定初始点出发,沿着使结构性能最优的方向生长和分枝,同时删除对结构性能贡献小的加强筋,逐步形成最优的加强筋布局。设计过程中,以单元的相对密度为设计变量,以单元灵敏度数作为判断加强筋单元生长和删除的准则。使用Python语言编写了基于ABAQUS的优化设计程序,利用ABAQUS进行有限元求解和前处理。为验证所提方法的有效性,以最大化结构整体刚度为设计目标,对几种典型结构进行了加强筋设计,并与现有文献中的设计结果进行了对比。
加强筋布局;结构优化;灵敏度数;刚度优化
0 引言
薄板加强筋结构在航空、船舶、汽车等领域有着极为广泛的应用,如光电平台框架、轻量化薄型反射镜和反射镜背板等都是典型的加强筋结构。通过在薄板表面布置加强筋,能够在保证结构轻量化的同时,显著提高结构的强度、刚度、振动等力学性能。
对加强筋进行布局优化设计,实现结构轻量化和承载性的双赢,一直是结构设计领域的难题。变厚度法[1]、均匀化法[2]、渐进结构优化法[3]等连续体拓扑优化方法都被应用到加强筋的布局优化设计中。这些方法通常将加强筋的布局问题转换为加强筋材料的分布问题,设计结果是加强筋大致的分布区域需要采用后处理手段进行识别。此外,一些学者采用直线或B样条曲线来描述加强筋,并利用遗传算法[4]、拓扑导数法[5]、粒子群算法[6]等方法对直线端点或样条曲线控制点的坐标进行优化设计。上述方法需要对加强筋进行参数化描述,虽然能够获得清晰的加强筋布局,但是难以处理具有复杂结构、承受复杂载荷的薄板结构加强筋布局优化问题。
仿生设计方法在该领域也有广泛应用。Kobayashi[7]提出了一种基于L系统的拓扑优化方法,并以最小化叶脉质量和压降为优化目标对植物脉序生长进行了模拟。马剑峰等[8]通过研究蜻蜓膜翅的结构特征,对飞机加强框进行了仿生设计。Stanford等[9]利用一种基于L系统的拓扑优化方法,通过模拟细胞分裂过程,对机翼的加强筋布局进行了优化设计。然而现有的研究通常只对特定承载条件下的具体结构进行仿生设计,只能解决有限的工程问题。Ding等[10]通过研究植物根系形态形成机理,提出了应用于薄壳结构加强筋设计的自适应成长设计法,已被成功应用到以最小柔度[11]和抗振性能[12]等为优化目标的加强筋优化设计中。该方法以加强筋的高度为设计变量,通过改变单元高度来逐步实现加强筋的生长和退化。本文提出了一种新的加强筋布局设计方法,并以结构整体刚度最大化为优化目标对典型的板壳结构进行加强筋布局设计,验证该方法的有效性。
1 加强筋布局设计的数学模型
以结构整体刚度最大化为设计目标,加强筋板的设计模型如图1所示。利用有限元技术,将加强筋板离散为板梁组合结构,基板采用四节点壳单元模拟,任意相邻壳单元的节点之间可创建两节点梁单元。采用这种基结构模型,能够避免网格重新划分。需要指出的是,由于本文仅涉及加强筋在基板平面内的二维布局,故为了便于建模分析,采用相同截面尺寸的矩形截面加强筋进行设计。
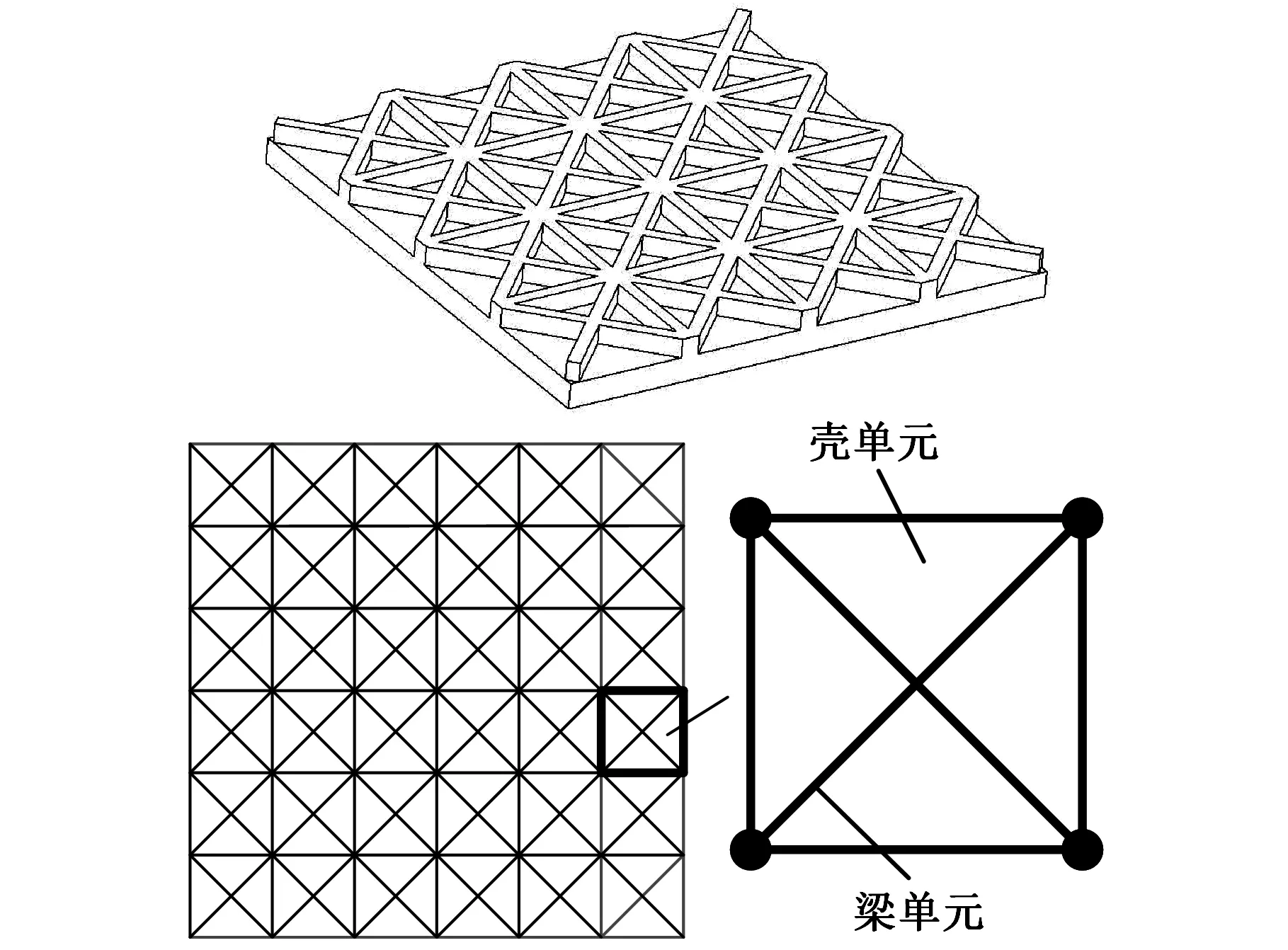
图1 加强筋板的基本设计模型
结构优化设计中,结构整体刚度通常采用结构在外载作用下的应变能来定量描述,对于上述板梁组合结构的刚度优化问题,在给定加强筋体积上限的情况下,其数学表达式如下:
(1)
其中,xi为第i个梁单元的相对密度;n为梁单元总数;E为结构的应变能,它是结构整体刚度的一个逆指标,最大化结构整体刚度等价于最小化应变能;f为载荷向量;u为位移向量;Vi为第i个梁单元的体积;V*为事先指定的体积上限。设计过程中,单元相对密度xi为离散设计变量,只允许两种取值,分别代表单元的两种状态:xmin为一个十分小的值(一般为0.001),表示未成长的空单元,1表示已成长的实体单元。空单元不被完全删除,可为单元生长提供必要信息。
2 加强筋布局设计方法
给定基板结构的条件下,加强筋布局的形成是一个逐步生长的过程。如图2所示,加强筋从若干给定的初始点出发,朝着使结构性能最佳,即应变能最小的方向生长和分枝,逐步添加对结构整体刚度贡献度最大的加强筋单元,同时删除贡献度最小的加强筋单元。每一步迭代中,所有已生长单元的节点都可以生长出新的加强筋单元,与之相连的所有空单元都是下一步迭代中的潜在生长单元。

图2 加强筋生长示意图
2.1单元灵敏度数
为了衡量加强筋单元对结构整体刚度的贡献程度,引入单元灵敏度数的概念。单元灵敏度数能够表征单元对于减小应变能、增大结构刚度的贡献程度,可作为加强筋单元生长和删除的判据。
首先采用伴随方法,计算结构应变能相对于第i个单元相对密度的偏导数:
(2)
其中,K为整体刚度矩阵。仅考虑与xi对应的单元位移向量和刚度矩阵,将单元灵敏度数定义为
(3)
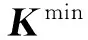
(4)
(5)
单元灵敏度数表示单元的生长和删除对目标函数的影响程度。实体单元灵敏度数表示删除某个单元可能导致的应变能增大值,灵敏度数越小,对减小目标函数的贡献越小。空单元灵敏度数可理解为添加某个单元可能导致的应变能减小值,灵敏度数越小,对减小目标函数的贡献越大。可以看出,无论是空单元还是实体单元,式(5)中灵敏度数的绝对值越大,单元的贡献度越高,因此,可将单元灵敏度数统一表示为
(6)
对于对称结构,位于对称位置的单元可能有相同的灵敏度数,为了避免一次添加过多加强筋材料,需考虑这些单元的总体积,对其灵敏度数取平均值:
(7)

2.2加强筋生长/删除准则和收敛条件
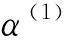
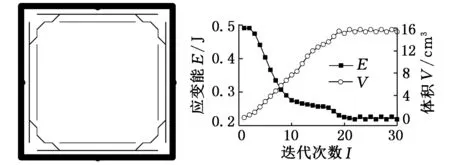
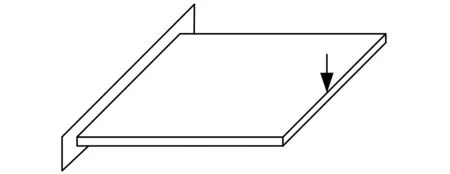
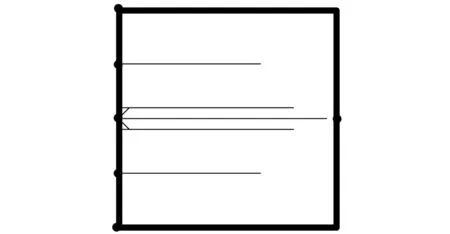
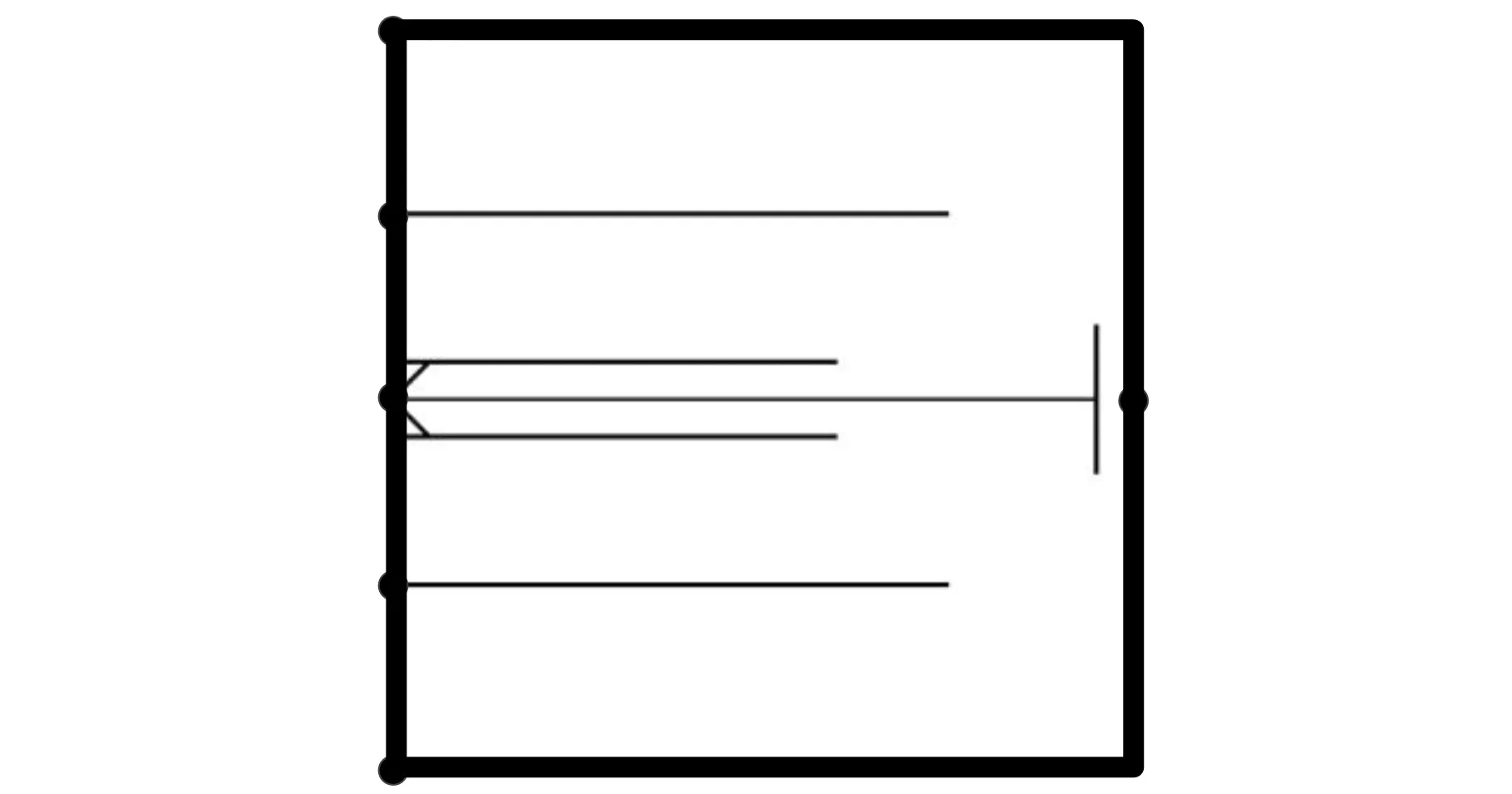
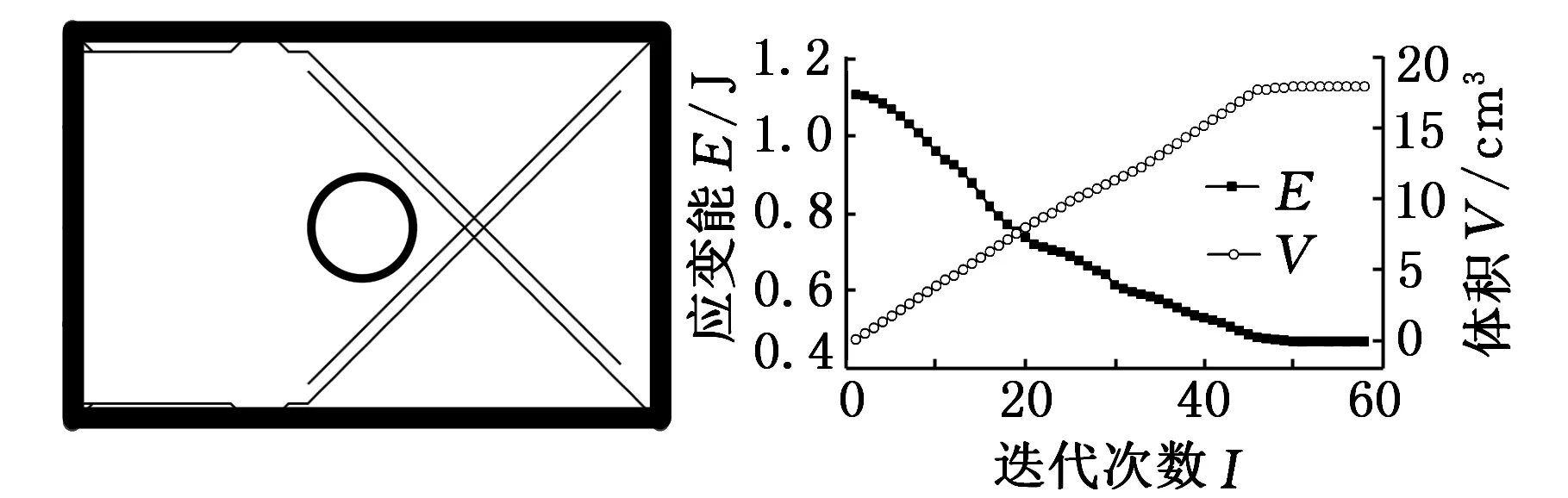
(1)单元生长:当加强筋体积V (2)单元删除:当加强筋体积V≥V*或满足以下条件: (8) 当同时满足体积约束V*和下列收敛条件: (9) 时,认为达到设计要求,停止迭代。其中,k为当前迭代步,τ为收敛精度,N是一个指定的整数。通常将N取为5,表示目标函数在最后10次迭代中的变化在可接受的范围内。 设计流程如图3所示。 图3 设计流程图 本文设计算法利用Python语言编译实现,并嵌入ABAQUS/CAE,调用ABAQUS进行有限元前处理和求解。为了验证所提方法的有效性,本节对几个典型算例进行了加强筋布局设计。本文所有算例均采用相同材料,弹性模量为70 GPa,泊松比为0.29,密度为2.85×103kg/m3。计算现有文献中所获得结果的应变能时,保持加强筋体积与本文算例相同。并且,由于本文研究的是加强筋在薄板平面内的布局问题,故假设加强筋的高度也相同。 3.1四点简支方板 图4所示的受集中载荷200 N的四点简支方板(仅约束平动自由度),模型几何参数如下:方板边长为200 mm、厚为2 mm,加强筋截面高为4 mm、宽为3 mm。设计参数设置如下:V*=0.2V0(V0为基板体积),r=0.5%,τ=0.001。由于结构的对称性,初始点的位置也应对称选取。除了初始点位于方板中心的情况,至少应选取4个初始点。设置了3组不同的初始点位置,加强筋的设计结果分别如图5~图7所示,文献[4]中采用遗传算法以及文献[10]中采用自适应成长法均获得图8所示的结果,其加强筋截面高为4 mm,宽为7.1 mm,保证其加强筋体积同样为0.2V0。图5~图7中黑点表示初始点,粗实线表示结构边界,细实线表示加强筋,结构边界上不布置加强筋,E0为未加筋基结构的应变能,I表示总迭代次数。 图4 四角简支方板的加载示意图 图5 四点简支方板的加强筋布局设计结果一 图6 四点简支方板的加强筋布局设计结果二 图7 四点简支方板的加强筋布局设计结果三 图8 四点简支方板的加强筋布局设计结果[10] 图5中的初始点位于四边中点,经历30次迭代收敛,最终结构应变能为0.45E0,是三种方案中优化效果最差的。图6中的初始点位于板的中心,图7中的初始点位于板的中心和四个支撑点,这两种方案的加强筋布局基本一致,仅在靠近支撑点的位置略有不同,分别经历32次和33次迭代收敛,最终结构应变能分别为0.32E0和0.31E0,图7的结果略优于图6的结果。图8中加强筋分布在板的对角线上,结构的应变能为0.36E0。文献[10]采用自适应成长法经历203次迭代才获得收敛的结果,这是因为它以加强筋单元的高度为设计变量,这是一个连续变量,每次迭代中通过一个启发式的公式来确定加强筋高度的生长量,需要确定的参数较多,且各参数的取值直接影响设计结果,其实质是一个尺寸优化过程,而本文采用的是离散变量,一次迭代中直接添加或删除单元。从以上结果可以看出,初始点应选择在支撑处和载荷作用处,而且采用本文方法获得的加强筋布局略优于文献[4,10]的结果。 3.2单边固支方板 图9所示的单边固支方板,自由边中点受法向集中载荷100 N,模型几何参数如下:方板边长为200 mm、厚为3 mm,加强筋截面高为5 mm、宽为3 mm。设计参数设置如下:V*=0.1V0,τ=0.001。为探讨不同的删除率r对设计结果的影响,分别将删除率设置为1%、0.5%、0.1%和0.01%,在载荷作用点和固支边布置了5个初始点。不同删除率获得的结果如图10~图13所示,图14所示为文献[4]获得结果,加强筋高为5 mm,宽为5.37 mm,图15所示为采用OptiStruct软件获得的结果。 图9 单边固支方板的加载示意图 图10 单边固支方板加强筋布局设计结果(r=1%,E=0.38E0) 图11 单边固支方板加强筋布局设计结果(r=0.1%,E=0.29E0) 图12 单边固支方板加强筋布局设计结果(r=0.5%,E=0.29E0) 图13 单边固支方板加强筋布局设计结果(r=0.01%,E=0.3E0) 图14 单边固支方板加强筋布局设计结果(E=0.41E0) 图15 单边固支方板加强筋布局设计结果(OptiStruct) 退化率为1%时,无法获得一个收敛的结果,迭代过程出现了“震荡”的现象,如图10所示,与轴线垂直的加强筋两端以及轴线两侧的两条加强筋末端的单元在迭代过程中不断地被重复添加和删除,迭代过程陷入死循环。退化率设置为0.1%和0.5%时,获得的结果完全一致,最终结构的应变能为E=0.29E0,优于文献[4]获得的结果,加强筋布局与采用OptiStruct软件获得的结果基本一致。退化率设置为0.01%时,获得的加强筋布局与退化率为0.5%和0.1%时的分布区域基本一致,但是各条加强筋的长度以及靠近受力点的位置略有不同,导致这种结果的原因是靠近载荷作用点的短加强筋以及外侧两条加强筋上的单元在迭代过程中没有被及时地删除,没有获得最优化的结果。 比较不同的删除率设置所获得的加强筋结果可知,删除率不宜过大或过小,如果过大则导致一些单元被错误地删除,并且可能使加强筋沿着错误的方向生长,使迭代陷入死循环;如果设置过小则不能及时地删除单元,在低效的位置浪费过多的材料,不能获得最佳的布局。删除率的选择不需要十分精确,只需在一定的范围内就能保证获得比较理想的结果。大量算例结果表明,将删除率设置在0.1%至0.5%之间能够获得最优化的加强筋布局。 3.3带孔悬臂矩形板 图16所示的受两个反向集中力100 N的带孔悬臂矩形板,模型几何参数如下:板长为300 mm、宽为200 mm、厚为3 mm,加强筋截面高为5 mm、宽为3 mm,中心孔径为50 mm。设计参数设置如下:V*=0.1V0,r=0.5%,τ=0.001。基板离散为30×20的四节点壳单元。在载荷作用点和固支边布置了7个初始点,设计结果如图17所示,图18所示为文献[5]采用拓扑导数法获得的结果,其加强筋高为5 mm,宽为4.63 mm。图19所示为采用OptiStruct软件获得的结果。 图16 带孔悬臂矩形板的加载示意图 图17 带孔悬臂矩形板的加强筋布局设计结果 图19 带孔悬臂矩形板的加强筋布局设计结果(Optistruct) 图17~图19中的三种加强筋布局基本一致,加强筋从载荷作用点出发,在孔的右侧交叉形成“X”形,最终延伸至固支边的两个端点。但是,图17中的加强筋在交叉处分为两股,形成了两个重合的“X”形,这样的布局与图19采用OptiStruct获得的加强区域完全一致,结构的应变能也远低于文献[5]的结果。 3.4中心支撑圆形薄板 图20所示的中心支撑圆形薄板,表面受均布载荷0.1 MPa。模型几何参数如下:基板直径为200 mm、厚为2 mm,加强筋截面高为5 mm、宽为3 mm,中心孔径为50 mm。设计参数设置如下:V*=0.15V0,r=0.1%,τ=0.001。由于其受均布载荷,在板的表面均布5个初始点,设计结果如图21所示。 图20 中心支撑圆板 图21 中心支撑圆板加强筋布局设计结果 历经23次迭代获得了收敛的结果,最终结构的应变能为0.19E0。可以看到,8条加强筋从约束点出发,呈放射状向边缘生长。图22所示为旱金莲叶的脉序布局,图23所示为文献[13]中利用Optistruct拓扑优化软件设计的中心支撑反射镜结构。这两种结构的支撑与载荷条件都与本算例类似。可以看到,采用本文方法获得的加强筋布局结果与旱金莲叶脉脉序和反射镜背部加强筋位置基本一致。 图22 旱金莲叶图23 中心支撑反射镜 本文提出的加强筋布局设计方法以单元灵敏度数作为加强筋生长和删除准则,逐步生长出最优加强筋布局。以最大化整体刚度为目标对典型的薄板结构进行了加强筋设计,通过与现有文献中的结果进行对比,验证了该方法的有效性。采用本文方法能够获得清晰的加强筋布局,显著地提高了结构的整体刚度。 该方法同样适用于任意目标函数和约束条件的优化设计问题。此外,基于ABAQUS的优化设计程序具有良好的开放性,可用于解决复杂结构的加强筋布局设计问题。 [1]Lam Y C, Santhikumar S. Automated Rib Location and Optimization for Plate Structures[J].Structural and Multidisciplinary Optimization, 2003, 25(1): 35-45. [2]Ansola R, Canales J, Tarrago J A, et al. Combined Shape and Reinforcement Layout Optimization of Shell Structures[J]. Structural and Multidisciplinary Optimization, 2004, 27(4): 219-227. [3]章胜冬, 杨军刚, 张卫红. 薄板结构加强筋布局设计的渐进结构优化方法[J].现代制造工程,2009(4): 5-9. Zhang Shengdong, Yang Jungang, Zhang Weihong. Evolutionary Structural Optimization for Stiffener Layout Problem of Plate Structures[J]. Modern Manufacturing Engineering, 2009(4): 5-9. [4]Fatemi J, Trompette P. Optimal Design of Stiffened Plate Structures[C]//Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Denver, 2002:1672. [5]Bojczuk D, Szteleblak W. Optimization of Layout and Shape of Stiffeners in 2D Structures[J].Computers & Structures, 2008, 86(13): 1436-1446. [6]Mulani S B, Slemp W C H, Kapania R K. EBF3PanelOpt: An Optimization Framework for Curvilinear blade-stiffened Panels[J]. Thin-Walled Structures, 2013, 63: 13-26. [7]Kobayashi M H. On A Biologically Inspired Topology Optimization Method[J].Communications in Nonlinear Science and Numerical Simulation, 2010, 15(3): 787-802. [8]马建峰, 陈五一, 赵岭, 等. 基于蜻蜓膜翅结构的飞机加强框的仿生设计[J].航空学报, 2009, 30(3): 562-569. Ma Jianfeng, Chen Wuyi, Zhao Ling, et al. Bionic Design of Aircraft Reinforced Frame Based on Structure of Dragonfly Wing[J]. Acta Aeronautica Et Astronautica Sinica, 2009, 30(3): 562-569. [9]Stanford B, Beran P, Kobayashi M. Simultaneous Topology Optimization of Membrane Wings and Their Compliant Flapping Mechanisms[J]. AIAA Journal, 2013, 51(6): 1431-1441. [10]Ding X, Yamazaki K. Adaptive Growth Technique of Stiffener Layout Pattern for Plate and Shell Structures to Achieve Minimum Compliance[J]. Engineering Optimization, 2005, 37(3): 259-276. [11]Ji Jin, Ding Xiaohong, Xiong Min. Optimal Stiffener Layout of Plate/shell Structures by Bionic Growth Method[J]. Computers and Structures, 2014, 135: 88-99. [12]丁晓红, 陈建来, 程莉. 抗振板壳结构的仿生拓扑优化设计方法[J].船舶力学,2008, 12(1): 125-130. Ding Xiaohong, Chen Jianlai, Cheng Li. A Bionic Approach of Topology Design Optimization for Vibration-proof Plate and Shell Structures[J]. Journal of Ship Mechanics, 2008, 12(1): 125-130. [13]陈程,刘伟,梁彪. 小口径离轴抛物面反射镜挠性支撑设计分析[J].计算机仿真, 2012, 29(8): 59-63. Chen Cheng, Liu Wei, Liang Biao. Design and Analysis of Flexible Support Structure for Off-axis Small-aperture Parabolic Reflector[J]. Computer Simulation, 2012, 29(8): 59-149. (编辑陈勇) Stiffener Layout Optimization of Thin Plate Structures Based on Sensitivity Number Li Lei1,2Zhang Bao1Li Quanchao1Tan Songnian1 1.Key Laboratory of Airborne Optical Imaging and Measurement,Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun,130033 2.University of Chinese Academy of Sciences,Beijing,100049 A heuristic design method for stiffener layout of thin plate structures was proposed herein. Starting from some prescribed initial nodes, the stiffeners grew and branched off towards the direction that the structural performance would be optimized. And the stiffeners with the minimum effectiveness on the structural performance were deleted simultaneously. During the design process, the relative density of each element was treated as the design variable. The growth and degeneration of the stiffeners were determined by the elemental sensitivity numbers. The design algorithm was programmed in Python and integrated with ABAQUS software which was used as the FEA preprocessor and solver. To validate the effectiveness of the proposed method, it was applied to design the stiffener layouts of some typical structures with the objective of maximizing the overall stiffness, and the obtained results were compared with the results in existing literatures. stiffener layout;structure optimization;sensitivity number;stiffness optimization 2015-12-15 国家自然科学基金青年科学基金资助项目(61405192);中国科学院国防科技创新基金资助项目(CXJJ-15S158) TH122 10.3969/j.issn.1004-132X.2016.09.002 李蕾,男,1989年生。中国科学院大学、中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室博士研究生。主要研究方向为结构优化设计。张葆,男,1966年生。中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室研究员、博士研究生导师。李全超,男,1989年生。中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室研究实习员。谭淞年,男,1989年生。中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室研究实习员。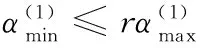


3 数值算例













4 结语

