呼吸系统pre-Bötzinger复合体中Ca2+振荡频率研究

张碧昭

(北京邮电大学理学院，北京 100876)

呼吸系统pre-Bötzinger复合体中Ca2+振荡频率研究

张碧昭

(北京邮电大学理学院，北京 100876)

实验研究表明，位于哺乳动物脑干部分的pre-Bötzinger复合体是呼吸节律产生的中枢。基于吸气神经元pre-BötC的耦合模型，通过改变参数IP3和VSERCA的值，对Ca2+振荡频率进行研究，我们发现随着参数值的变化，Ca2+的振荡频率也呈现着周期性变化。

pre-Bötzinger复合体；振荡；簇放电；峰放电

1 引言

呼吸系统中的病态呼吸节律一直是人们关注的、影响着人类健康的问题，研究呼吸系统动力学的一个重要目标，就是在了解呼吸系统正常的动力学行为的基础上，进一步研究病态呼吸节律产生的动力学机制，从而实现对病态呼吸节律的控制。同时，运用非线性动力学的理论和方法，研究神经生理过程更符合自然界基本规律。

十九世纪九十年代初，研究者们对新生大鼠进行实验研究，认为pre-Bötzinger复合体可能是新生哺乳动物呼吸节律起源的关键部位[1]；随后的研究表明在pre-Bötzinger中存在一类具有振荡簇发放的兴奋性神经元，这类神经元的节律性簇放电与呼吸节律的产生密切相关[2]；在实验研究的基础上，研究者们提出了一些神经元网络模型，其中Butera等人于1999年提出了关于簇放电产生的两种模型：模型1中，簇放电开始于快速激活的持续钠电流并终止于慢速失活的持续钠电流[3]；模型2中，簇放电产生于快速激活的持续钠电流而终止于慢速激活的持续钾电流[4]；国内外也有很多学者对于神经网络在不同领域的应用进行了研究[5-8]；Caiteri和Rubin等人从不同的拓扑结构出发，研究了不同拓扑结构对神经元放电模式的影响[9]；Izhikevich运用分岔分析的方法研究了神经元的可兴奋性、峰放电以及簇放电的性质，并对神经元簇放电进行了分类[10]；Toporikova等人建立了pre-BötC的轴突和树突模型并研究了Ca2+的振荡情况和相应簇放电的类型[11]；此后段等人利用快慢变量分离和双参数分岔分析等方法，研究了Na+和K+变化时耦合神经元放电模式对单个神经元放电模式的依赖机制[12]。

因此，研究呼吸节律的产生机制对于研究人体和其他动物体的基本生理活动具有及其重要的实际意义，同时对治疗与呼吸节律有关的疾病也有重要的指导意义。本文中所用的pre-BötC模型是由Park和Rubin[13]提出的，文章中所有图像均由XPPAUT[14]画出。

2 模型的建立

我们根据Park和Rubin[13]和Butera[3][4]给出pre-BötC耦合模型如下：

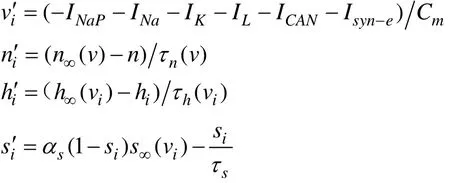
有关钙离子的动力学特征可以描述为：f([Ca])=1/(1+(K/[Ca])nCAN)，d[Ca]/dt=f(J-i CANi iiERINJEROUT)，dli/dt=AKd(1-li)-A[Ca]ili.

其中，

在上述模型中，对于x∈{mp,m,h,n,s}，有x∞(v)=从，并且对于{h,n}

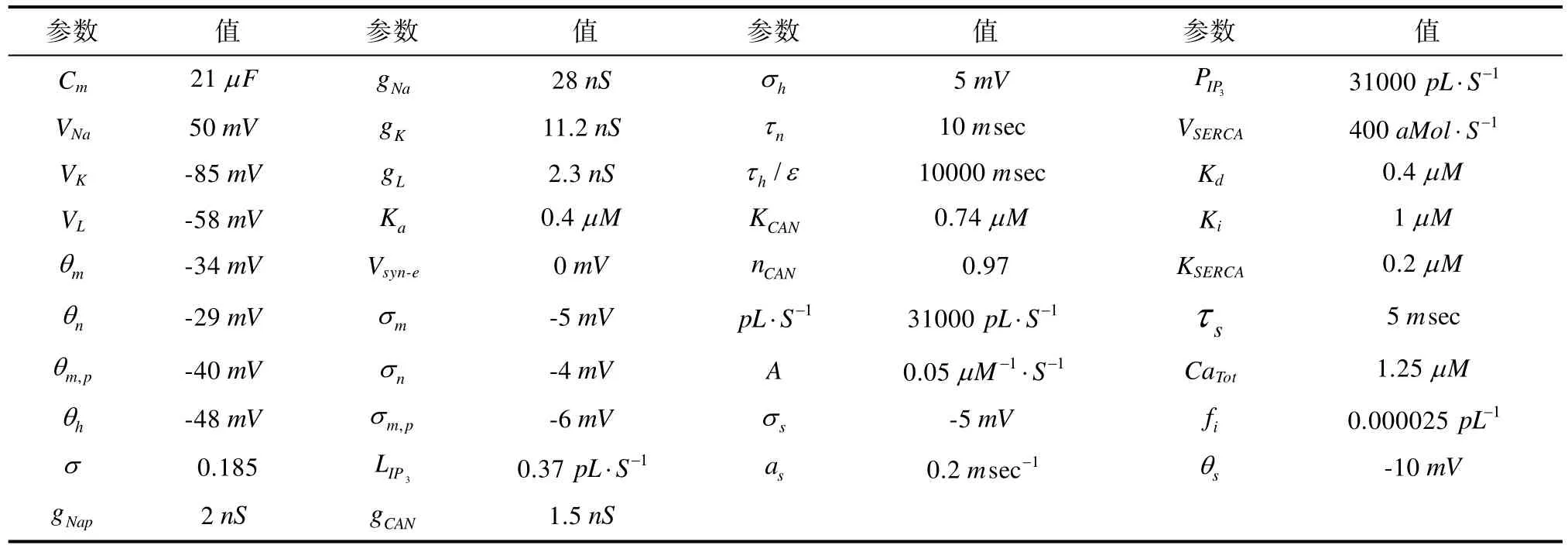
表1 模型中的参数值

3 Ca2+振荡频率研究

经过研究分析，可以得到影响Ca2+振荡频率的两个关键参数：IP3和VSERCA。下面将分别进行论述。

3.1 参数IP3对Ca2+振荡频率的影响

这里，我们假设VSERCA=400是固定的，我们只通过变化IP3的值来观察Ca2+振荡频率的变化规律。我们分别取IP3等于0.90、0.95、1.1、1.41，此时我们可以得到对应的时间序列图（Fig.1(a)(b)(c) (d)）；同时，我们选取Ca为慢变量，且令Ca= Ca1=Ca2，我们可以得到Ca随h变化的序列图（Fig.2(a)(b)(c)(d)）。通过图像分析，我们可以得到当IP3=0.95时，开始出现Ca2+振荡；当0.95＜IP＜1.41时，放电模式为簇3放电，且Ca2+振荡的频率逐渐增加；当IP3＞1.41时，开始出现峰放电。

3.2 参数VSERA对Ca2+振荡频率的影响

这里，我们选取IP3=1，我们只变化VSERCA。分别取VSERCA等于271、280、350、426，此时，我们可以得到相应的时间序列图（Fig.3(a)(b)(c)(d)）；同样的，我们可以得到Ca随h变化的序列图（Fig.4(a)(b)(c)(d)）。当VSERCA变化的时候，随着VSERCA增大，Ca2+振荡逐渐消失：当VSERCA＜271时，图像呈现峰放电；当271＜VSERCA＜426时，放电模式为簇放电，且Ca2+振荡的频率逐渐减小；当VSERCA＞426时，Ca2+振荡消失。

图1 IP3变化时的时间序列图。(a)IP3=0.90 (b) IP3=0.95 (c) IP3=1.1 (d) IP3=1.41

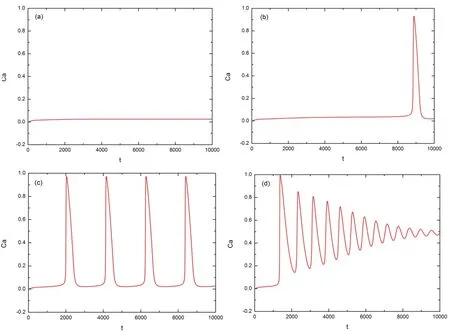
图2 IP3变化时Ca2+振荡图。(a)IP3=0.90 (b) IP3=0.95 (c) IP3=1.1 (d) IP3=1.41

图3 VSERCA变化时的时间序列图。(a) VSERCA=271 (b) VSERCA=280 (c) VSERCA=350 (d) VSERCA=426

图4 VSERCA变化时Ca2+振荡图。(a) VSERCA=271 (b) VSERCA=280 (c) VSERCA=350 (d) VSERCA=426

4 结语

本文我们在呼吸系统pre-Bötzinger复合体耦合模型的基础上，分别改变IP3、VSERCA的参数值，发现Ca2+振荡频率呈现着周期性变化。当改变IP3的值时，Ca2+振荡频率静态到逐渐增大，最后出现峰放电；当改变VSERCA的值时，Ca2+振荡频率的变化正好相反，由峰放电到逐渐减小，最后变为静态。

有关其他参数值对Ca2+振荡频率的影响有待进一步探讨，上述得到的Ca2+的振荡频率的变化，也可以为下一步研究提供帮助。

[1] SMITH J C, ELLENBREGER H H, BALLANYI K, et al. Pre-Bötzinger complex: a brainstem region that may generate respiratory rhythm in mammals [J], Science, 1991, 254-726.

[2] REKLING J C, FELDMAN J L. Pre-Bötzinger complex and pacemaker neurons: Hypothesized site and kernel for respiratory rhythm generation [J]. Ann. Rev. Physiol., 1998, 60: 385-405.

[3] BUTERA R J, RINZEL J, SMITH J C. Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons [J]. Neurophysiol., 1999, 82: 382-397.

[4] BUTERA R J, RINZEL J, SMITH J C. Models of respiratory rhythm generation in the pre-Bötzinger complex. II. Populations of coupled pacemaker neurons [J], Neurophysiol., 1999, 82: 398-415.

[5] 邢海花, 陈焕东, 林红燕.基于输入扰动的分层混合模糊-神经网络敏感性分析[J]. 软件, 2013, 34(2): 52-55.

[6] 刘玉海. 神经网络的C编程及矿井安全预测仿真[J]. 软件, 2013, 34(5): 88-90.

[7] 马莉雅. 基于决策树、逻辑回归和改进神经网络的几种慢性病的危险因素分析研究[J]. 软件, 2014, 35(12): 58-65.

[8] 张敏, 徐启华. 基于改进BP的神经网络模型参考自适应控制[J]. 软件, 2015, 36(7): 118-123.

[9] GAITREI C, RUBIN J E. The interaction of intrinsic dynamics and network topology in determining network burst synchrony [J]. Front. Comput. Neurosci., 2011, 5: 10.

[10] EUGENE M. IZHIKEVICH. Neural excitability, spiking and bursting, International Journal of Bifurcation and Chaos, Vol. 10, No. 6, 2000, 1171-1266.

[11] TOPORIKOVA N, BUTERA R J. Two types of independent bursting mechanisms in inspiratory neurons: an integrative model[J]. Journal of Computational Neuroscience, 2011, 30(3): 515-528.

[12] DUAN L X, ZHAI D H, TANG X H. Bursting induced by excitatory synaptic coupling in the pre-Bötzinger complex [J]. Int. J. Bifurcation Chaos, 2012, 22, 1250114.

[13] PARK C, RUBIN JE. Cooperation of intrinsic bursting and calcium oscillations underlying activity patterns of model pre- Bötzinger complex neurons. J Comput Neurosci 2013; 34: 345-366.

[14] ERMENTROUT B. Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. SIAM 2002.

The research on the frequency of Ca2+oscillations in the pre-Bötzinger complex

ZHANG Bi-zhao
(School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876)

Experimental investigations have shown that the pre-Bötzinger complex (pre-BötC) within the mammalian brainstem generates the inspiratory phase of respiratory rhythm. Based on the coupling model of pre-Bötzinger, we study the oscillation frequency of Ca2+by changing the value of IP3and VSERCA. We find that with the change of the parameter values, the oscillation frequency of Ca2+also presents a periodic change.

Pre-Bötzinger complex; Oscillation; Bursting; Spiking

O193

A

10.3969/j.issn.1003-6970.2016.10.023

张碧昭(1993-)，女，研究方向：微分方程及动力系统。

本文著录格式：张碧昭. 呼吸系统pre-Bötzinger复合体中Ca2+振荡频率研究[J]. 软件，2016，37（10）：105-108