随心潜入“桥” 建构细无声——以《乘法分配律》教学为例

●刘　敏

随心潜入“桥” 建构细无声
——以《乘法分配律》教学为例

●刘敏

人教版《数学》四年级下册的《乘法分配律》是一节比较抽象的教学内容，是乘法简便运算定律教学中的重点，也是学生学习时需要克服的难点之一。学生在学习这个知识点时，常常出现各式各样的错误，如（a+b）×c=a×c+b。在面对乘法分配律变换的不同类型时，更是应接不暇，慢慢地学生就产生了畏难情绪。为了扫除学生思维上的障碍，在教学时，教师要潜心为学生铺路搭桥，合理地架构起支撑点，顺利地让学生思维过渡到理想的节点，并在探索活动中发现、感悟、体验建构概念。

一、借助生活情境，主动建构

建构主义理论认为：学生的数学学习是一个主动建构的过程。借助情境这一较为直观的载体，把生动的生活情境融入到教学实践，唤起学生的相关经验，形成解决问题的策略，从而赋予抽象的算式以鲜活的生命。这样的概念才不会是干瘪、乏味的，这样的知识，学生才会感到有趣、有味、有价值。

例如，在教学时，笔者创设了这样的情境：六一儿童节，学生要代表学校去市里参加文艺汇演，需要套装20套，其中上衣每件40元，裤子每条30元，问一共需要多少元？有的学生说，可以先求一套服装的价格是40+30=70（元），再求20套的总价是70×20=1400（元），还有的学生说，可以分别求20件上衣的总价是40×20=800（元）和20条裤子总价是30×20=600（元），再将其相加是800+600=1400（元）。也就是说（40+ 30）×20=40×20+30×20，恰到好处地解释为什么“（a+b）×c不等于a×c+b”，通过联系学生熟悉的生活场景，创设教学情境，让学生初步感知乘法分配律在生活中的运用。接着，笔者继续设问“如果套数改变了，利用两种方法计算出来的总价结果还会相等吗？”引导学生进行知识迁移。最后把订购的套装数量用“c”来表示，让学生经历了由特殊到一般，由具体到抽象的数学化过程。通过巧妙地变换数，为乘法分配律的构建搭建阶梯。

二、利用几何直观，建立模型

越是抽象的数学对象，其数学本质越有可能用简洁直观的图形来表达。几何直观可以帮助学生直观地理解数学，利用图形把数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。

在教学时，笔者出示了下图图形，让学生计算该长方形的面积。

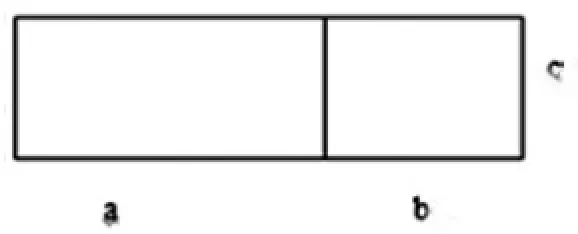
学生的思路有两种，一种是：用a×c表示左边图形的面积，用b×c表示右边图形的面积，然后把这两个长方形的面积相加。另一种是：大长方形的长是a+b的和，然后再乘它的宽c，也是整个图形的面积，两种方法都是求它们的面积，所以，学生就很容易理解（a+b）× c=a×c+b×c。不仅规范了学生的数学语言，训练了学生的数学思维，而且为理解乘法分配律找到直观雏形。

三、巧用童趣语言，完善建构

艺术的语言处理，将枯燥无味、晦涩难懂的数学变得生动形象且有趣，利于学生理解接受。有趣的故事串联，能够激发学生的探究兴趣，扫除学生的思维障碍，加深学生对知识的理解，从而帮助学生构建知识网络。

在学生知道什么是乘法分配律后，笔者问学生“分配”是什么意思？学生说就是把（a+b）打开分别跟c相乘。“分”就是分别，“配”就是配对。笔者借机让学生和爸爸妈妈配对，体会母子、父子间的情意。看谁会把一句话“我爱爸爸和妈妈”改成等价的两句话“我爱爸爸，我也爱妈妈”。此时再联系乘法分配律的计算公式（a+b）× c=a×c+b×c。它瞬间变得鲜活起来，减少了类似“（a+b）×c=a×c+b”的错误。乘法分配律变式练习中最难理解的是隐藏了一个因数后的公式应用，需要学生先找出该因数，再进行公式运算。教学时，笔者让学生观察算式“38×99+38”，学生发现“妈妈”藏起来后，引导学生找到妈妈，学生发现“妈妈”一直都在那里，就是那个默默无闻的“1”，至此巧妙地破解了学生的思维障碍。

教师要成为教学的有心人，要不失时机地为学生搭建突破难点的阶梯，让学生多角度、多方位地去体验、去建构！

（作者单位：襄阳市大庆路小学教育集团）

责任编辑孙爱蓉

责任编辑严芳