双曲螺线的主法线曲面的相关性质研究*1

包　弘，梁　林（云南师范大学数学学院，云南 昆明 650092；楚雄师范学院数学与统计学院，云南 楚雄 675000）

数摇学

双曲螺线的主法线曲面的相关性质研究*1

包弘，梁林
（云南师范大学数学学院，云南 昆明 650092；楚雄师范学院数学与统计学院，云南 楚雄 675000）

本文以双曲螺线为背景，生成曲面为研究对象，讨论了三维欧氏空间中双曲螺线的主法线曲面的几何性质.获得了双曲螺线的主法线曲面的渐近曲线、曲率线、法曲率、主曲率、高斯曲率、平均曲率等，并给出了简单应用。

双曲螺线；主法线曲面；平均曲率；高斯曲率；主曲率

微分几何学家常致力于一些特殊曲面的研究，以期扩宽曲面的知识。由于主法线曲面属于可展曲面的范畴，因此对主法线曲面的研究可丰富可展曲面的相关内容。所谓的主法线曲面是指，一条曲线的主法线所产生的直纹面。袁媛、刘会立在文［1］中分别得到了特殊曲线Mannheim曲线，Bertrand曲线主法线曲面的一些相关性质。由于一般螺线也和Mannheim曲线，Bertrand曲线一样具有良好的几何和代数性质，本文受此启发，讨论了双曲螺线的主法线曲面，给出了双曲螺线的主法线曲面的相关几何性质。

1.预备知识

定义1［2］主法线曲面是由曲线r→（t）的主法线生成的直纹面.设β→（t）为曲线r→（t）上任意一点P的主法向量，则曲线r→（t）的主法线曲面Σ为

引理1［2］曲面的第一基本形式：

定义3［2］曲面上的一点P处满足Ldu2+2Mdudv+Ndv2=0的方向du：dv称为曲面在P点处的渐近方向.曲面上的曲线的每一点的切方向都是渐进方向的曲线，称为渐进曲线，其微分方程为Ldu2+2Mdudv+Ndv2=0.

引理4［2］曲面的第二基本形式：

则曲率线微分方程为

其中kN为主曲率，主曲率满足：

其中k1、k2为曲面上一点的两个主曲率.高斯曲率为：

平均曲率为：

2.主要结论

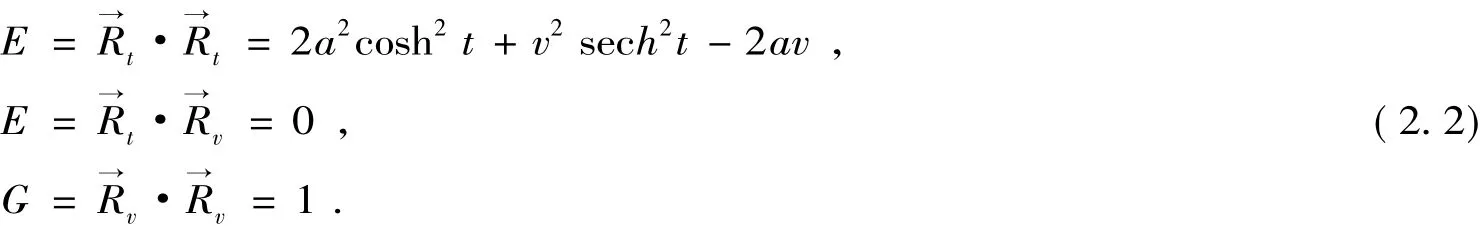
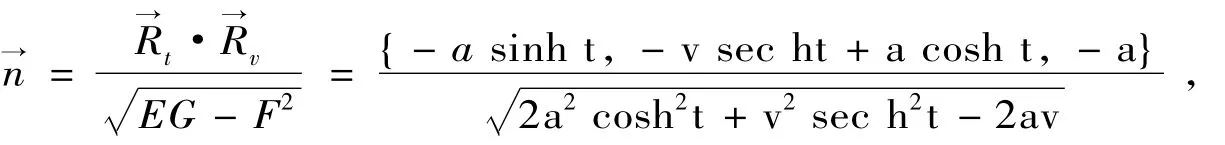
定理2.4双曲螺线的主法线曲面的另一族非直线渐近曲线的微分方程为

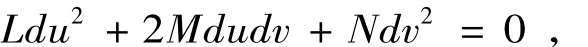
定理2.6双曲螺线的主法线曲面上的曲率线微分方程为

证明双曲螺线的主法线曲面的主曲率满足（1.5），其中F=N=0，整理得EG-LGkN-M2=0，把（2.2），（2.3）代入得记双曲螺线的主法线曲面的主曲率为k1，k2，由求根公式即得。

定理2.9双曲螺线的主法线曲面的高斯曲率为

定理2.10双曲螺线的主法线曲面的平均曲率为

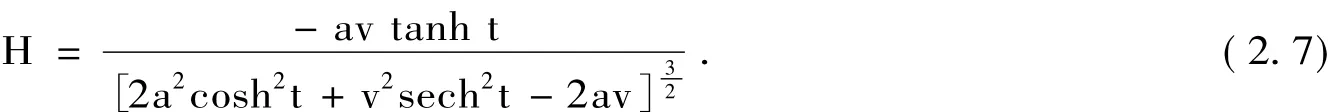
定理2.12双曲螺线的主法线曲面的极小曲面不存在.

当且仅当t=0时，sinh t=0，tanh t=0.这与假设矛盾，故双曲螺线的主法线曲面的极小曲面不存在.

定理2.13双曲螺线的主法线曲面不可能是平面或球面.

证明若双曲螺线的主法线曲面是平面或球面，则主曲率相等，即k1=k2，则

这与（2.6）中双曲螺线的主法线曲面的K＜0矛盾.

［1］袁媛，刘立会.曲面的主法线曲面［J］.东北大学学报，2007，28（1）：145—148.

［2］梅向明，黄敬之.微分几何［M］.高等教育出版社，2008.

（责任编辑李艳梅）

Research on the Related Properties of Hyperbolic Spiral's Principal Normal Surfaces

BAO Hong&LIANG Lin
（School of Mathematics，Yunnan Normal University，Kunming，650092，Yunnan Province；School of Mathematics and Statistics，Chuxiong Normal University，Chuxiong，675000，Yunnan Province）

The hyperbolic spiral as the background，surface generation as the research object，discusses the geometric properties of hyperbolic spiral's principal normal surfaces in the Euclidean three-space ，hyperbolic spiral's principal normal surfaces of asymptotic curves，curvature method，principal curvature，Gaussian curvature，mean curvature all be obtained in this paper，and gives some simple application.

hyperbolic spiral；principal normal surfaces；mean curvature；Gaussian curvature；principal curvature

O186.16

A

1671-7406（2016）03-0001-05

楚雄师范学院国家自然科学基金孵化项目。

2016-01-05

包弘 （1990—），女，硕士研究生。梁林 （1967—），男，教授，研究方向：微分几何。