基于点集的拉伸建模改进方法
杨 乃,贾 跃,苏黎兰,万 林,杨 洁
(1. 中国地质大学信息工程学院,湖北 武汉 430074; 2. 扬州市城市规划编制研究中心,江苏扬州 225002; 3. 中国地质大学公共管理学院,湖北 武汉 430074)
基于点集的拉伸建模改进方法
杨乃1,贾跃2,苏黎兰3,万林1,杨洁1
(1. 中国地质大学信息工程学院,湖北 武汉 430074; 2. 扬州市城市规划编制研究中心,江苏扬州 225002; 3. 中国地质大学公共管理学院,湖北 武汉 430074)
探讨了拉伸建模存在公共基元重复构建、侧面空间关系丢失、产生冗余基元等拓扑问题,指出了不同地物三维模型两个侧面之间拓扑关系存在的12种表现形式,提出了基于点集的自动拉伸建模方法,并分别介绍了点集的提取流程和体的构建流程,最后通过一个实例证明了以上方法对传统拉伸建模方法在拓扑关系方面存在的不足有所改进。
拓扑关系;拉伸建模;三维建模;空间关系;地图可视化
拓扑关系是最重要的一种空间关系[1-2],是空间查询与分析的基础[3],已广泛应用于制图综合、空间推理、空间数据挖掘等实际应用中[4]。拓扑关系不一致将会导致空间认知错误,影响地图的传输效果[2]。当前,三维模型的拓扑构建与分析已成为3DGIS的主要研究内容之一[5-10]。
以拉伸(Extrusion)的方式建立三维模型是3DGIS及三维建模软件中常见的一种建模方法,尤其适用于具有规则形体结构的地物模型构建,如建筑物。这种建模方法往往不会考虑地物之间的拓扑关系,导致出现诸如公共面重复、垂直方向上空间关系丢失等问题,建立的模型常常仅限于可视化表达,无法进行进一步的空间分析[11]。针对这些问题,文献[12]将整个区域的建筑和地形统一用一张Delaunay三角网表示,实现了类似拉伸的效果,但无法表达两个相邻建筑的垂直公共面;文献[11]和文献[13]基于约束性Delaunay三角网构建了拓扑一致的三维城市模型,其中产生的若干点、若干面仍然可以进一步综合以降低拓扑复杂性。本文将对此进行改进,提出一种基于点集的自动拉伸建模方法,能够改进传统拉伸建模方法在拓扑关系方面存在的若干不足。
一、拉伸建模拓扑问题分析
三维空间中,体与体之间的拓扑关系共有8种[8-14],在三维地籍与房产管理领域,建筑物的体对象之间只有相离和相邻关系[5-6],其底面也仅对应存在这两种关系。拉伸建模是将一系列描述体状地物底面的多边形按指定高度进行拉伸拔高以形成块状多面体的三维建模方法,最适用于上述建筑体模型的建立[11],如图1所示。这种方式建立的三维模型主要存在如下拓扑问题。
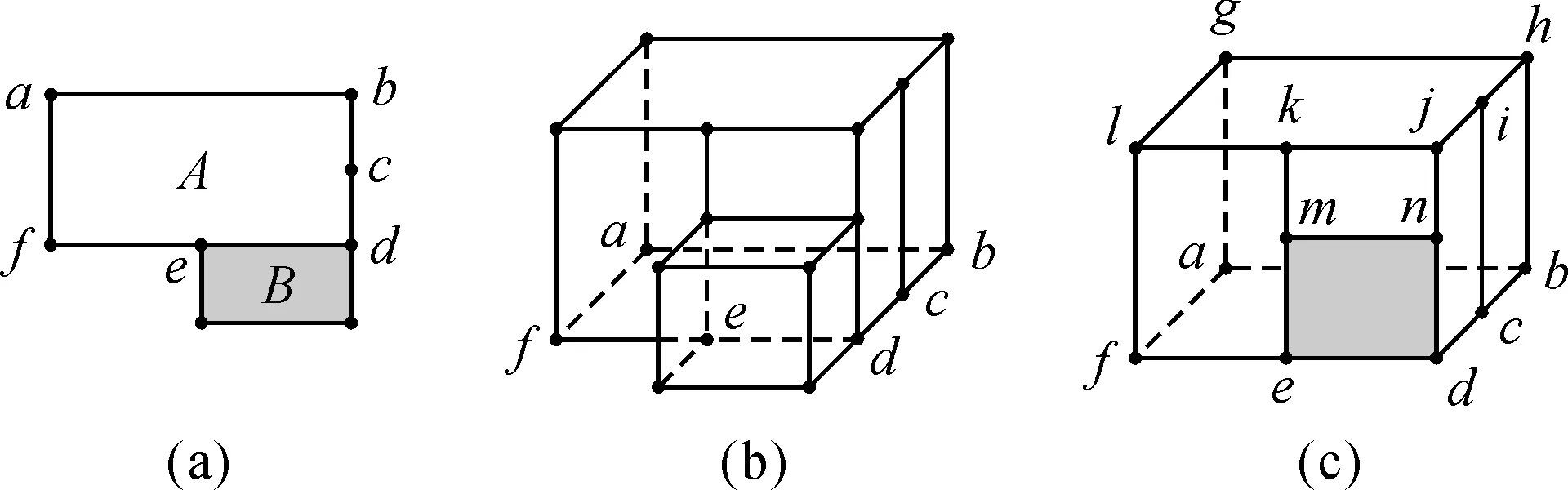
图1 拉伸建模图示
1. 公共基元重复构建
结点、边、面和体是4种拓扑基元[6],如图1(a)所示,多边形A、B是俯视条件下相邻地物的两个底面示意图,因高度不同,通过拉伸之后形成的三维模型如图1(b)所示,其中,二者公共的部分(图1(c)中mnde)的结点、边、面在A、B拉伸时被分别构建。
2. 侧面空间关系丢失
如图1所示,即使底面A、B之间存在拓扑关系,但拉伸建模之后,侧面形成的结点、边、面,如图1(a)边def对应的侧面(图1(c))中共形成8个结点、10条边、3个面,它们之间的相互关系并没有得到有效存储,不利于垂直方向上的空间分析。
3. 产生冗余基元
上文中公共基元重复构建将产生一些重复的基元。此外,还会产生一些不必要的基元,具体如下:
1) 在底面数据采集时,经常会出现多点重合的现象,拉伸建模后,顶面对应将会产生重合点。
2) 底面边线中间的若干节点拉伸建模后,在顶面形成对应的节点,在对应侧面上被拉伸成为一条条直线,将侧面分割为多个子侧面。如图1(a)边bcd拉伸后,点c在顶面对应形成点i,并被拉伸为直线ci,将侧面bdjh分割为面bcih和面cdji(如图1(c)所示)。
3) 多个具有不同高度属性的底面相接时,某些公共点拉伸建模后将会导致冗余基元的产生。如图1(a)所示,底面A与底面B高度属性不同,拉伸建模后,边def对应的侧面理应被分割为具有相接关系的2个子侧面,但实际上被划分为3个子侧面(如图1(b)、图1(c)所示),其原因在于底面A拉伸后在点e对应的顶面边上产生了多余点k,侧面上产生了多余边km。文献[11]和文献[13]尚未解决该问题。
二、侧面拓扑关系分析
上述拓扑问题主要体现在三维模型侧面上,根据拉伸建模原理,侧面不可能出现岛、洞等情况,只能是规则的简单多边形。简单多边形存在8种拓扑关系[15-18],但拉伸形成的三维模型侧面之间只存在相离、相接、相交、覆盖、覆盖于、相等6种拓扑关系。以2个地物为例,具体表现形式有12种(如图2所示)。
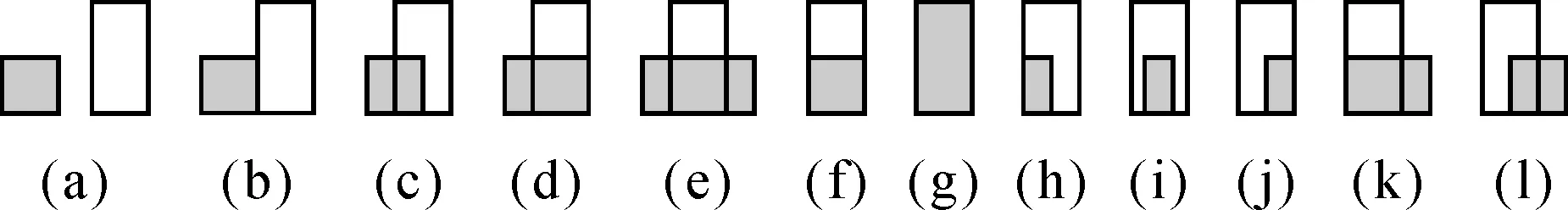
图2 侧面拓扑关系
其中,图2(g)表示两个侧面存在相等关系,图2(c)和图2(l)、图2(d)和图2(k)、图2(h)和图2(j)尽管对称,但因地物之间的高度及判断目标的先后顺序不同,本文实现过程并不相同,因此将其列在图2中。对于2个以上的地物,拉伸建模后可能出现一个三维模型侧面与其他多个三维模型侧面存在拓扑关系的情况,但也只是图2各种情况的排列组合,本文每次只需考虑两个侧面即可。
三、基于点集的自动拉伸建模方法
为解决上述问题,本文首先根据地物高度及其底面之间的拓扑关系,提取一系列点,然后基于这些点构建三维模型的各个面,最终由这些面封闭构成体。
1. 点集的提取
构成三维模型的点集主要包括底面、顶面的结(节)点及侧面上与其他三维模型相关联的点。
(1) 底面重合点的处理
要避免拉伸建模后产生重合点,首先必须对底面重合点进行处理。重合点可以通过坐标值是否相同进行判断,也可以通过点与点之间的拓扑关系进行判断,找出重合点之后,只需保留其中一个点即可。
(2) 底面及顶面非拐点的处理
当节点关联的两条边之间的夹角为180°,称之为非拐点。非拐点是拉伸建模产生冗余基元的重要因素,主要表现为:①底面边上的非拐点,但与其他底面没有关联关系,拉伸后导致顶面边上也产生非拐点,如图3中的点a,拉伸后顶面形成非拐点d,并在侧面形成边ad;②底面边上的非拐点,与其他底面存在关联关系,同时也是其他底面的非拐点,拉伸后导致两个三维模型的顶面边上都产生非拐点,如图3中的点b,拉伸后在两个顶面上分别形成非拐点e和f,并在侧面形成边be、ef;③较高三维模型底面上的非拐点,与其他底面存在关联关系,但不是其他底面的非拐点,拉伸建模后在较高三维模型顶面形成非拐点,如图3中的c点拉伸后在底面A对应的三维模型顶面形成非拐点h。这些非拐点并不需要提取,主要通过与之相关联的两条边之间的夹角是否为180°来判断。
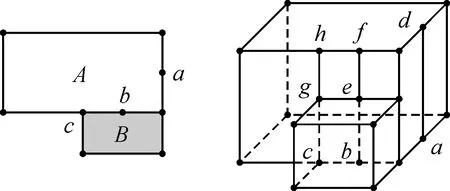
图3 非拐点示意图
(3) 顶面及侧面点的提取
顶面点是指顶面轮廓边上的点,侧面点是指侧面内域及与底面垂直的侧面边上的点。对独立地物而言,不存在侧面点,构建顶面点时,x、y坐标值与对应底面点相同,z坐标在对应底面点z坐标值基础上增加地物高度值即可。对与其他地物相邻的地物而言,底面点与其他底面不存在关联关系时,其对应顶面点的构建方法与独立地物相同;底面点与多个底面相关联时,则根据关联底面的高度属性从低到高排序,依次构建侧面点,其中当多个关联底面高度属性值相等时,对应只构建一个侧面点,各侧面点x、y坐标值与对应底面点相同,z坐标在对应底面点z坐标值基础上增加各关联底面高度属性值即可。
(4) 拓扑信息存储
提取点集之后,需存储各点与底面及底面点的对应关系,为方便后续体的构建,还需存储各点的高程值及其排序。如图4所示,具有同一底面关联点的各点,可以通过高程值或高程排序判断各点在Z方向上的连通关系;具有不同底面关联点的各点(如点3、点4),可以通过底面关联点的排列序号及是否存在相同关联底面来判断在XY平面上是否存在连通关系等。

图4 点的拓扑信息
2. 体的构建
若不考虑侧面拓扑关系,底面点数为n时,拉伸建立的三维模型由n+2个面组成,但实际如上文所述,当地物相邻时,某些侧面将被分割为若干个子侧面,组成三维模型的面数将大于n+2。因此,在体的构建过程中,为保证侧面拓扑关系的正确性,最重要就是通过以上点集构建存储拓扑信息的各个面。
(1) 底面构建
根据点集存储的拓扑信息,找到地物关联的底面点,连接封闭即可。
(2) 顶面构建
在点集中找到与底面点对应且高度属性值为地物高度的点,连接封闭即可。
(3) 侧面构建
根据上文分析可知,底面点在顶面上不一定有对应的点,如图5中点c,因此在构建侧面时,以顶面点为基准,在两个连通顶面点对应的底面点之间寻找是否存在共享子侧面,有则先构建该共享子侧面,再判断这两个连通顶面点与对应底面点之间是否还存在非共享子侧面,有则继续构建该非共享子侧面。如图5所示,连通顶面点B、g对应的底面点A、d之间存在共享子侧面,从点A开始寻找连通的底面点c,从点集中找到点A、c对应的侧面点a、b,由这4个点即可构建共享子侧面Aabc,构建完成后接着构建顶面点B、g与底面点A、d之间存在的非共享子侧面aBgdcb,非共享子侧面由共享子侧面顶面点、不存在共享子侧面的底面边结点、连通顶面点共同构成。
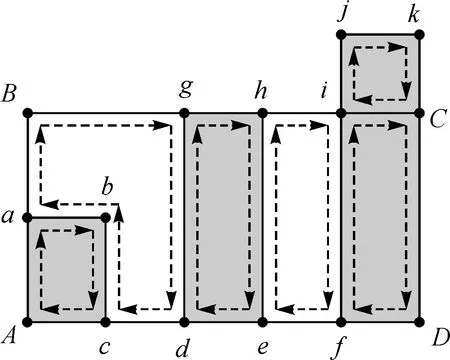
图5 侧面构建图示
(4) 体的构建及拓扑信息存储
建立顶面、底面及侧面后,为便于体的构建及空间查询与分析,需存储各面的类型信息,并建立4种拓扑基元的关联关系,其中,建立面-面、面-体、体-体的拓扑关系是以拉伸的方式建立保持正确拓扑关系的三维地物模型的基础。文献[5]和文献[6]指出了体的拓扑关系构建模型,由于拉伸建模形成的顶面、底面及侧面都与底面点存在对应关系,因此,本文提出的方法中各面都记录了底面关联点。这样,通过底面关联点就可以判断各面之间的拓扑关系,如图5所示,侧面aBgdcb的底面关联点为点A、c、d,侧面Aabc的底面关联点为A、c,根据上文的侧面拓扑关系分析及两个面的共享基元点,很容易判断两者是相接关系。此外,对于顶面、底面而言,记录包含它们的归属体及与它们有共享拓扑基元的关联体;对于非共享子侧面而言,记录包含它们的归属体;对于共享子侧面而言,记录包含它们的所有关联体(如图6所示)。通过这种存储方式,为面/面、面/体、体/体之间的空间查询与分析提供了便利,构建体时只需根据以上存储的拓扑信息找到相应的顶面、底面及侧面封闭即可。
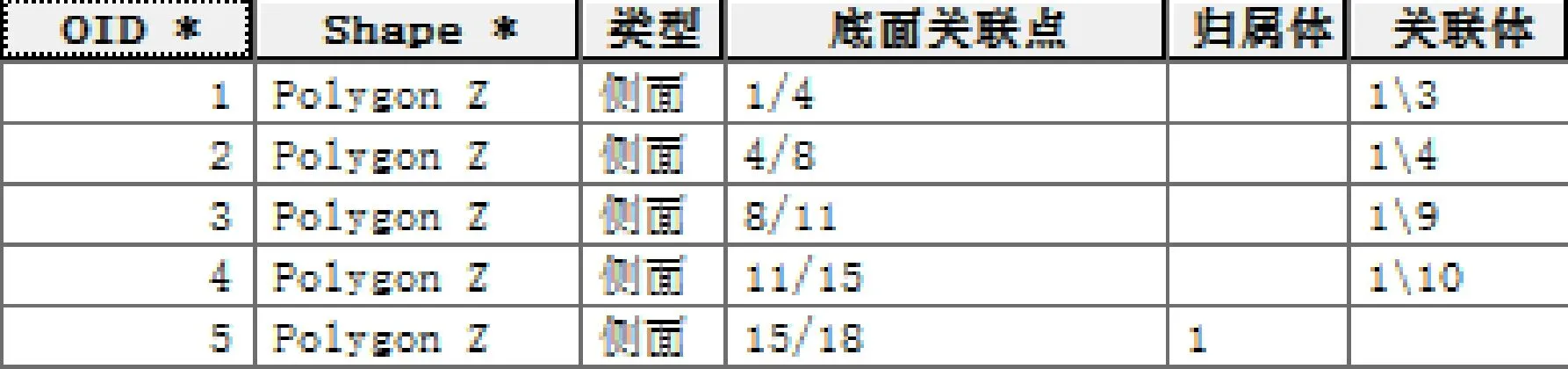
图6 面的拓扑信息
3. 试验与分析
本文基于VB.net+ArcGISEngine对以上方法进行了试验,图7(a)为某小区底面数据,提取点集后的结果如图7(b)所示,最终提取点数为119个,而常见拉伸建模方法形成的点数为228个。基于提取的点集建立的三维模型如图7(c)所示,该方法很好地解决了底面带洞、岛等复杂多边形的建模问题。图7(d)为ArcScene提供的Extrusion功能拉伸后的结果,将其与图7(c)对比,二者内部结构不同(图7(c)和(d)中底部区域),本文建立的体模型结构更加简单。此外,如图7(e)所示,本文提出的方法还可用于基于面的空间查询与分析。
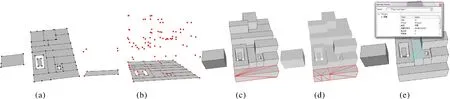
图7 试验与分析
四、结束语
本文顾及三维模型的拓扑关系,提出了基于点集的自动拉伸建模改进方法,能够改进拉伸建模在拓扑方面存在的若干不足。相比常见的拉伸建模方法,该方法提取的点数较少,并且随着地物底面多边形数及拓扑关系复杂性的增加,点数的减少量还将大大增加,以此构建的体的内部结构得到了简化,并能提供面/面、面/体、体/体之间的空间查询与分析。尽管如此,由于拉伸建模形成的三维模型还存在一些弱点[5],对于侧面为非规则多边形、顶面非平行于底面的地物来说,如何建立保持其拓扑一致性的三维模型还有待进一步研究。
[1]邓敏,李志林,李光强. 简单面目标与带孔洞面目标间拓扑关系的层次表达方法[J]. 测绘学报, 2008,37(3):330-337.
[2]詹陈胜,武芳,翟仁健,等. 基于拓扑一致性的线目标空间冲突检测方法[J]. 测绘科学技术学报,2011,28(5):387-390.
[3]吴信才. 地理信息系统原理与方法[M]. 北京: 电子工业出版社, 2009: 48-51.
[4]邓敏,马杭英. 线与面目标间拓扑关系的层次表达方法[J]. 测绘学报,2008,37(4):507-513.
[5]郭仁忠,应申,李霖. 基于面片集合的三维地籍产权体的拓扑自动构建[J]. 测绘学报,2012,41(4):620-626.
[6]李霖,赵志刚,郭仁忠,等. 空间体对象间三维拓扑构建研究[J]. 武汉大学学报(信息科学版),2012,37(6):719-723.
[7]贺彪,李霖,郭仁忠,等. 顾及外拓扑的异构建筑三维拓扑重建[J]. 武汉大学学报(信息科学版),2011,36(5):579-583.
[8]刘新,刘文宝,李成名. 三维体目标间拓扑关系与方向关系的混合推理[J]. 武汉大学学报(信息科学版),2010,35(1):74-78.
[9]邓念东,侯恩科. 三维体元拓扑数据模型的修正及其形式化描述[J]. 武汉大学学报(信息科学版),2009,34(1):52-56.
[10]陈鹏,孟令奎,宋杨. 三维GIS中基于空间拓扑约束条件的R树研究[J]. 武汉大学学报(信息科学版),2007,32(4):347-349.
[11]LEDOUXH,MEIJERSM.TopologicallyConsistent3DCityModelsObtainedbyExtrusion[J].InternationalJournalofGeographicalInformationScience,2011, 25(4):557-574.
[12]TSEROC,DAKOWICZM,GoldCM,etal.BuildingReconstructionUsingLiDARData[C]∥Proceedingsof4thISPRSWorkshoponDynamicandMulti-dimensionalGIS.Pontypridd,Wales,UK:[s.n.], 2005:156-161.
[13]LEDOUXH,MEIJERSM.ExtrudingBuildingFootprintstoCreateTopologicallyConsistent3DCityModels[J].UrbanandRegionalDataManagement-UDMSAnnuals,2009(1): 39-48.
[14]ZLATANOVAS,RAHMANAA,SHIW.TopologicalModelsandFrameworksfor3DSpatialObjects[J].Computers&Geosciences, 2004(30):419-428.
[15]刘波,李大军,邹时林,等. 带孔洞面域间的拓扑关系的组合推理[J]. 测绘学报,2011,40(2):262-267.
[16]沈敬伟,闾国年,温永宁,等. 拓扑和方向空间关系组合描述及其相互约束[J]. 武汉大学学报(信息科学版),2011,36(11):1305-1308.
[17]汪西莉,覃婧婵,曹菡,等. 基于SRC-Ontology的空间拓扑关系拓展表示方法及实现[J]. 武汉大学学报(信息科学版),2009,34(3):339-343.
[18]刘波,李大军,阮见,等. 带空洞面对象间拓扑关系形式化描述[J]. 武汉大学学报(信息科学版),2009,34(1):68-71.
ImprovedExtrusionModelingMethodBasedonPointSet
YANGNai,JIAYue,SULilan,WANLin,YANGJie
2015-05-26
国家自然科学基金(41201474;41401449)
杨乃(1984—),男,博士,讲师,主要研究方向为三维地图可视化。E-mail:naigeer@163.com
P208
B
0494-0911(2016)05-0041-04
引文格式: 杨乃,贾跃,苏黎兰,等. 基于点集的拉伸建模改进方法[J].测绘通报,2016(5):41-44.DOI:10.13474/j.cnki.11-2246.2016.0151.

