一种北斗卫星差分码偏差估计方法
赵东旭,遆 鹏,2,3,谭诗腾,3,唐 建
(1. 西南交通大学地球科学与环境工程学院,四川 成都 611756; 2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756; 3. 西南交通大学教育部轨道交通安全协同创新中心,四川 成都 611756; 4. 新疆维吾尔自治区建筑设计研究院,新疆 乌鲁木齐 830002)
一种北斗卫星差分码偏差估计方法
赵东旭1,遆鹏1,2,3,谭诗腾1,3,唐建4
(1. 西南交通大学地球科学与环境工程学院,四川 成都 611756; 2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756; 3. 西南交通大学教育部轨道交通安全协同创新中心,四川 成都 611756; 4. 新疆维吾尔自治区建筑设计研究院,新疆 乌鲁木齐 830002)
卫星码偏差会降低卫星测量精度,因此本文就北斗卫星差分码偏差估计进行了研究和验证。首先将电离层作为一个单层,采用球谐函数来参数化电离层TEC值,然后利用最小二乘估算了北斗卫星的码偏差,根据北斗系统2014年4月1—29日间的实测数据计算了14颗北斗卫星的码偏差,最后将计算结果与IGS发布的码偏差参考值进行了对比分析。结果显示误差值在0~2ns之间,符合度极高,从而验证了该估计方法的有效性。
北斗系统;M_DCB;码偏差;估计方法
北斗系统是我国自主研发建设的第一代卫星导航系统,在我国社会各方面建设中发挥着越来越重要的作用[1]。在北斗系统实用中,能否精确估计差分码偏差(differentialcodebiases,DCB)对于导航定位、精密测量至关重要。差分码偏差是指硬件延迟造成的同一时刻不同频率或同一频率上不同测距码观测量之间的时间偏差,一般为纳秒级。研究表明,卫星和接收机的码偏差是利用观测数据解算电离层总电子含量(totalelectroncontent,TEC)的主要误差源[2],而TEC是研究电离层建模的重要参数,1ns的码偏差可能造成2.86TECU(1UTEC=1×1016N·e/m2)的TEC误差[3],最终降低卫星测量的精度。本文拟针对码偏差的估计进行研究。
目前,国内外有许多关于码偏差估算方法的研究,但主要是针对GPS[4-7]。由于GPS和北斗系统各项参数存在差异,且北斗观测范围目前只覆盖亚太区域,对北斗系统的码偏差估计研究仍需深入。当前国内一些科研人员对北斗系统码偏差估计进行了相关研究。戴连军等利用北斗单星三频载波数据估算码偏差,即通过北斗单星三频电离层组合,线性回归假设及载波硬件延迟模型估算接收机码偏差[8],但是该方法只用来估算接收机码偏差,而卫星码偏差也会降低定位精度,需要进行估算。戴伟等通过探究GPS和Galileo导航卫星发射通道频间偏差参数TGD的由来及其使用方法,推导了北斗系统频间偏差参数的使用方法[2],但并没有进行实际数据的验证。
针对这些问题,本文基于文献[9]所提出的GPS观测数据解算卫星及接收机码偏差估计的思想,针对北斗系统提出一种改进的码偏差估计方法,并通过真实数据进行验证。
一、码偏差估计原理
本文首先将北斗卫星的观测值进行组合,并对组合观测值进行平滑,然后将电离层看作一个单层,通过最小二乘估计的方法,计算得到码偏差估计结果。基本流程如图1所示。
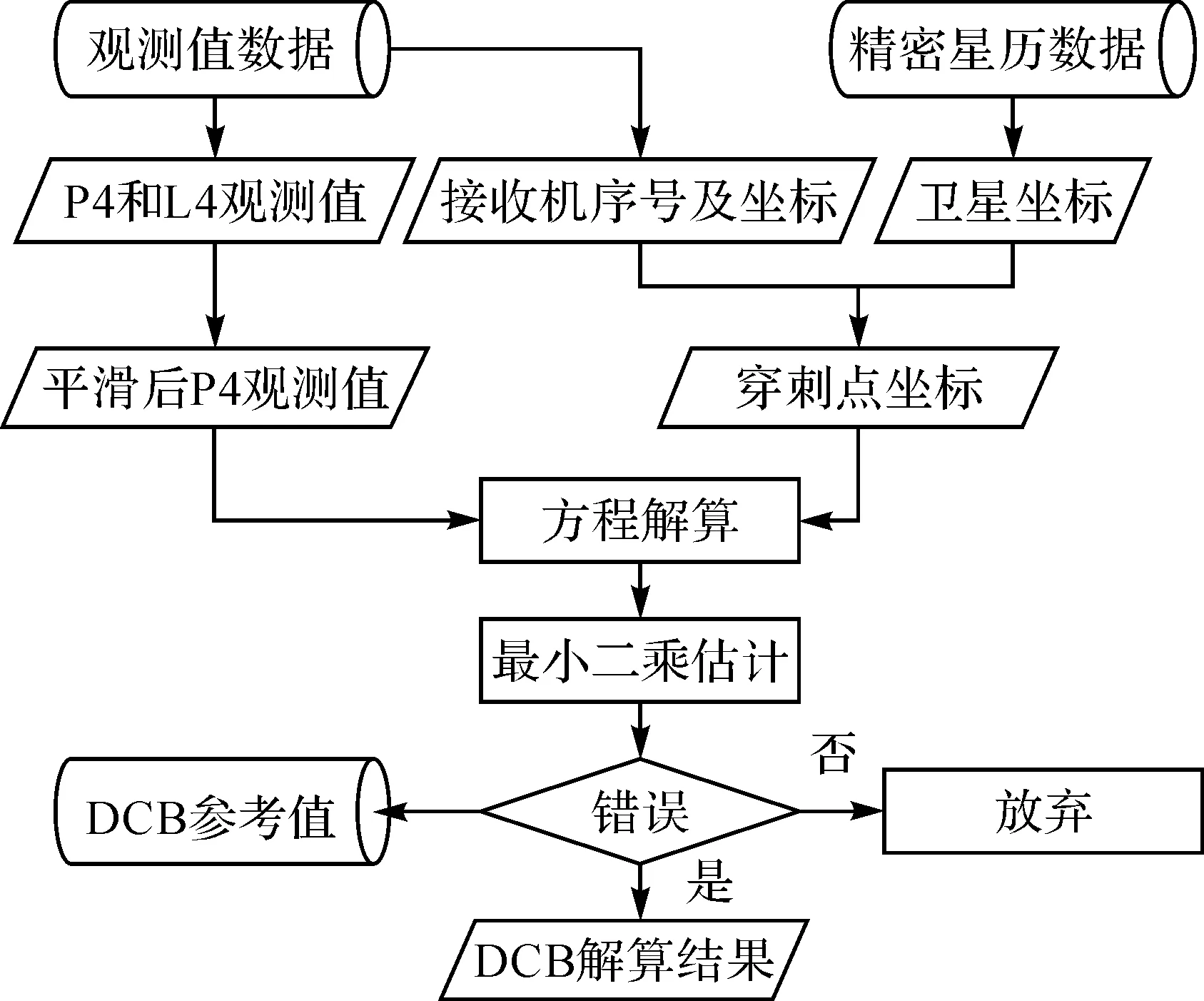
图1 DCB解算流程
1. 数据预处理
北斗系统伪距测量和载波相位测量的基本原理如下
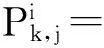
(1)
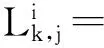
(2)
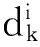
在上述原理的基础上,对同一颗卫星的不同测距码观测值或不同载波相位观测值进行同种信号间求差,可以消除卫星信号传播过程中电离层延迟误差和码偏差以外的大部分误差,得到组合观测值P4。其计算公式为
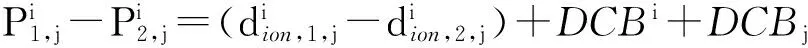
(3)
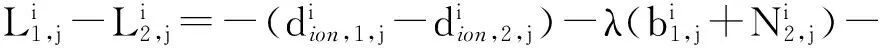
(4)
以上通过伪距观测值组合获得的组合观测值P4中含有测量噪声,这些噪声会削弱码偏差的估计精度。为了尽量提高码偏差估计结果的精度,在进行最终的解算之前,先利用载波相位观测值对P4进行平滑处理。平滑后的伪距观测值可表示为
P4,sm=ωtP4(t)+(i-ωt)Pprd(t)(t>1)
(5)
式中,t为历元数;ωt为与该历元相关的重力因素。
将改正结果代入到P4的表达式即式(3)中,可得到平滑后的观测值为
(6)
2. 解算DCB
经过组合观测值平滑处理后,可以利用观测数据得到更好的码偏差估计值。由式(6)可得到
(7)
STEC会随着卫星倾角的减小、信号传播路径s的增长而产生较大的变化,这不利于研究。因此,本研究中引入了不会受到卫星高度角及高程影响的VTEC。VTEC可以由STEC进行投影得到
VTEC=MF(z)STEC
(8)
(9)
式(9)中,z为卫星高度角;R为地球半径;H为电离层厚度。R一般设定为6371km。
假设电离层所有的电子都集中在一个无限薄的单层上,用这个单层来代替整个电离层进行研究。卫星信号穿过电离层这个假定的单层时,与单层的交点称之为穿刺点,如图2所示。
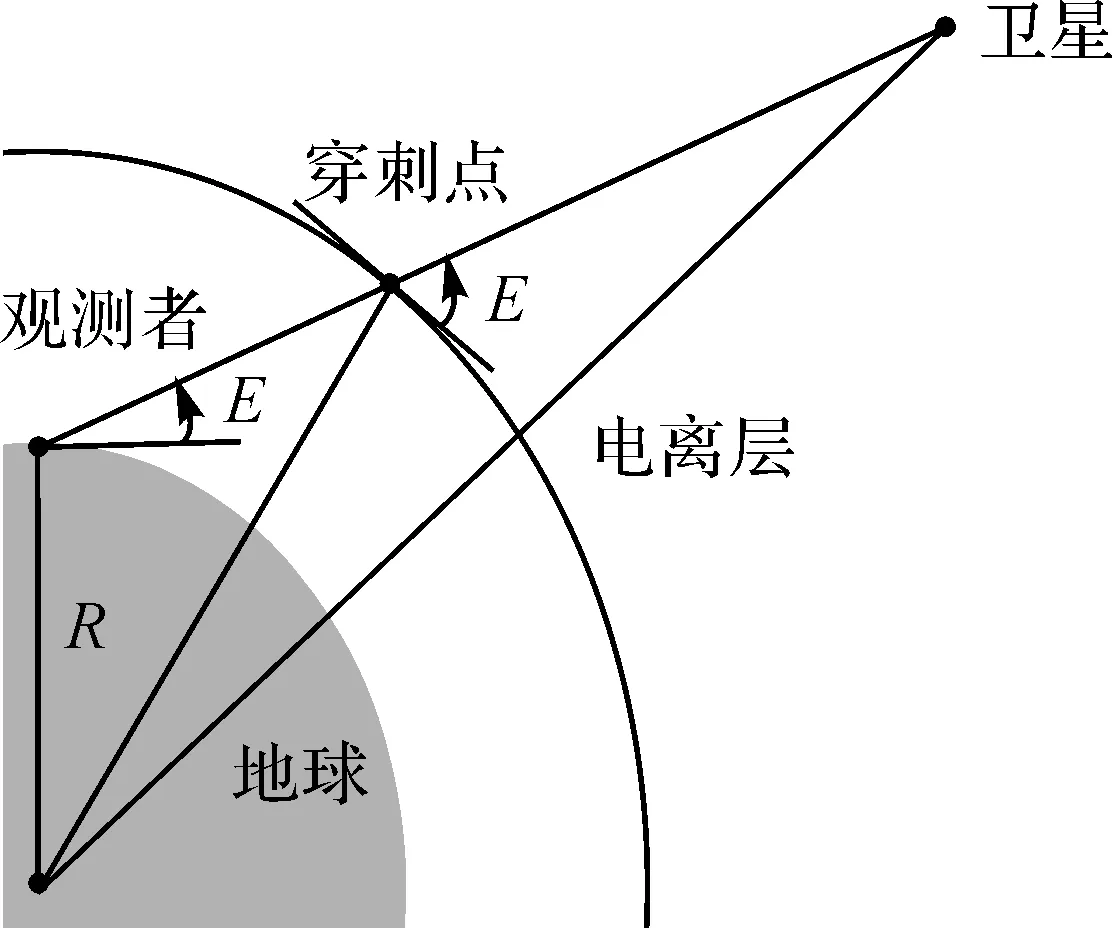
图2 电离层信号传播示意[10]
采用球谐函数来参数化VTEC,可以得到
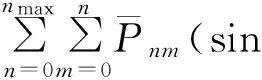
bnmsin(ms))
(10)
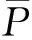
(11)
式中,δ为可替换的符号,可以用下面的表达式求得并替换
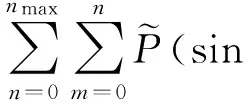
(12)
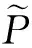
二、试验分析
1. 数据选择
试验中处理的数据为2014年4月1日至4月29日(年积日为91—119)期间的观测数据及精密星历数据,来源于MGEX测站上提供的卫星测量数据。处理观测历元个数在50万个以上,且测站在亚太地区覆盖率较好,能较好地反映北斗系统的状态;时间覆盖接近一个月的长度,便于与IGS发布的码偏差参考值进行比较,并分析和改进结果的可靠性和准确性。
2. 数据读取与参数设置
在MEGX提供的观测值数据文件中,存在以下几个问题:①数据文件中包含GPS、GLONASS及北斗系统等多个卫星导航系统的观测值数据;②对于可观测到北斗卫星的测站,其中一部分只能观测到少数北斗卫星的数据,如FAA1、BRU0等,只能观测到5颗卫星的信号;③部分测站观测到的北斗卫星信号的类型不全。
针对以上问题,本文对M_DCB进行了改进。首先,选取观测数据质量相对较好的测站(如GMSD、CUT0),以保证数据具有足够的观测卫星数和完整的信号类型;其次,在Matlab 2012a平台上实现了针对北斗数据的观测值文件读取;然后,针对GPS和北斗系统信号频率等参数不一致的问题,设置了合适的参数,使其与北斗系统适应;最后,解算了北斗卫星的码偏差。
3. 解算结果分析
在数据处理时段内,每个测站均得到14颗北斗卫星的码偏差估计值。图3为比较有代表性的4号卫星和11号卫星的码偏差估计值与参考值的比较结果。其中,横坐标表示2014年4月的日期;纵坐标表示码偏差的数值,单位为纳秒。
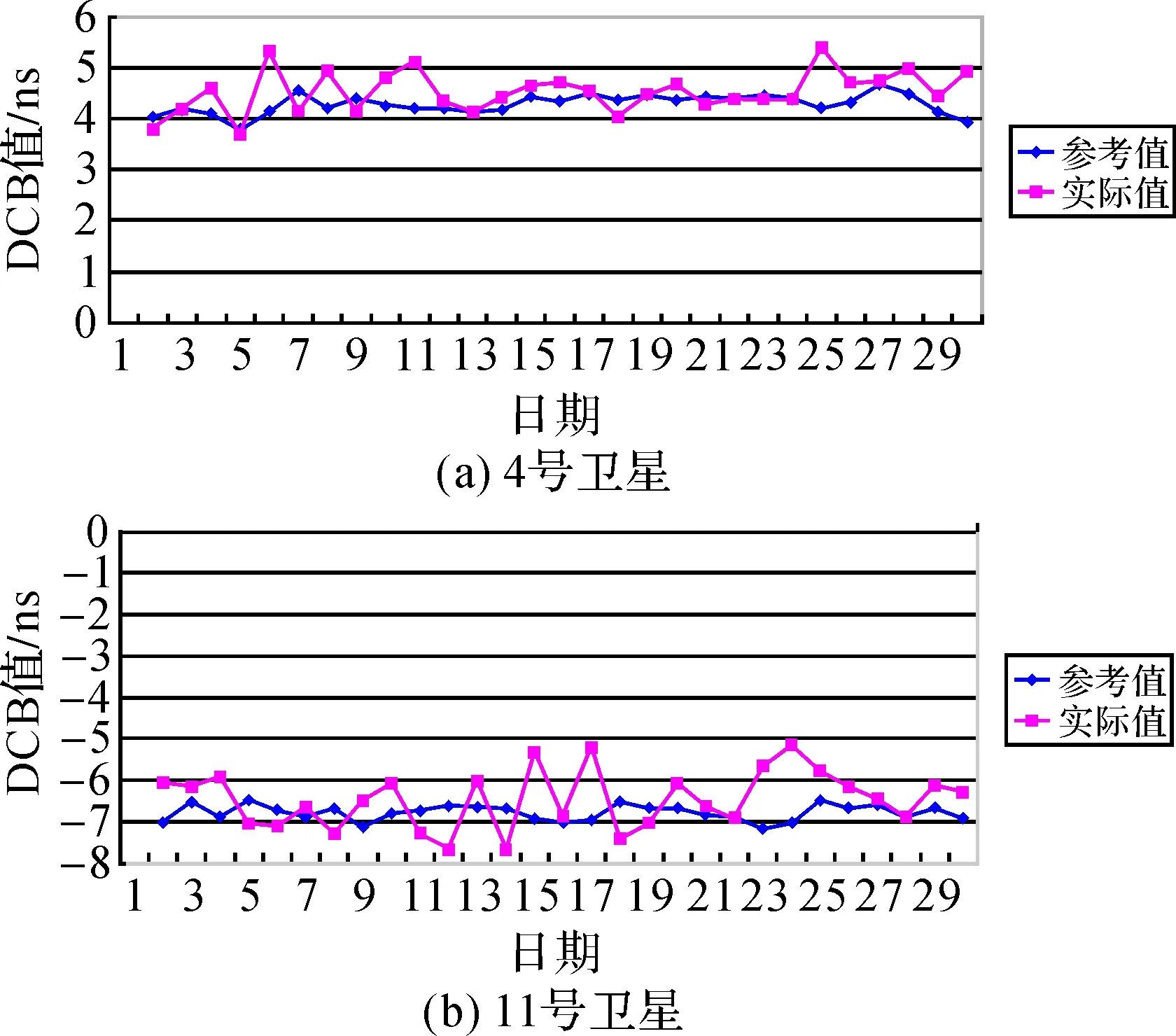
图3 DCB解算结果与参考值比较
通过图3可以发现,码偏差估计值与参考值的差值在2 ns以内,但估计值的相邻日期之间差值较大,即没有参考值变化趋势平稳;另外,个别日期的码偏差解算结果与参考值差距偏大,如11号卫星在4月24日的码偏差计算结果与参考值相差接近2 ns。对于本身就是纳秒级的码偏差来说,这种差值仍然偏大。
造成以上现象的原因有如下几点:
1) 不同时间采集到的卫星观测数据质量存在着差异。
2) 个别卫星的观测数据相对较少,如13号卫星。
3) 试验中所采取的测站数相对IGS发布码偏差参考值所用的测站数要少很多,总体数据量相差较大,使码偏差估计值与参考值之间的差异被放大。
图4为14颗卫星的DCB解算结果和DCB参考值的差值散点图,横轴为2014年4月的日期;纵轴为码偏差解算结果和参考值的差值,单位为纳秒。图中不同颜色代表不同的卫星的码偏差。可以看到,多数卫星在一些日期的码偏差解算结果和参考值的差值接近2 ns,此外,差值接近1 ns的日期也相对较多。可见,估计值变化趋势没有参考值平稳的问题,是几乎所有北斗卫星估算结果共同存在的问题。引起这些问题的原因与前面所分析的原因相同,这里不再重复。
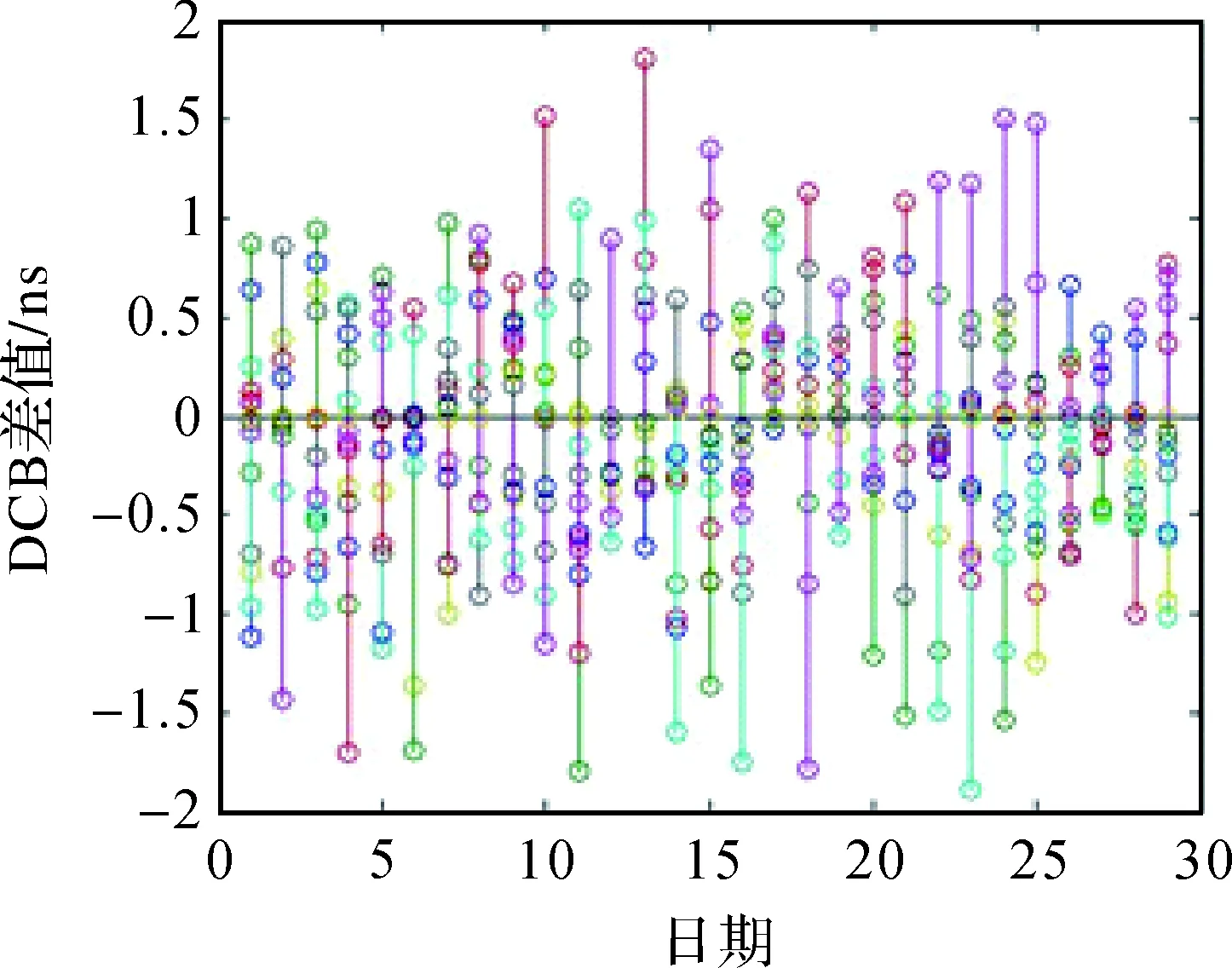
图4 DCB差值散点图
通过图4可以看出,14颗卫星的码偏差解算结果和参考值的差值都在2 ns内,说明解算结果总体精度可靠。
三、结束语
码偏差是影响TEC确定的主要误差源,降低了电离层延迟误差的精度,以致影响卫星测量的精度,因此,估算和改正码偏差具有重要意义。本文在M_DCB的基础上进行了改进,使其可以提取观测文件中的北斗数据,在设置合适的参数后,计算了北斗卫星的码偏差,并与IGS发布的参考值进行了比较分析,符合度极高,从而验证了该方法的可行性。但对于解算结果变化趋势不够平稳和个别日期与参考值差值偏大的问题,仍需在后续的研究中继续探讨。
[1]张荣群,张小栓,高万林,等. 北斗导航系统在农业领域的应用展望[J]. 测绘通报, 2012(S1):685-686.
[2]戴伟,焦文海,贾小林. Compass 导航卫星频间偏差参数使用方法[J]. 测绘科学技术学报, 2009, 26(5):367 -369.
[3]常青,张东和,萧佐,等. GPS硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报, 2001, 44(5):596-604.
[4]袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 北京:中国科学院(测量与物理研究所), 2002.
[5]章红平,韩文慧,黄玲,等. 地基GNSS全球电离层延迟建模[J]. 武汉大学学报(信息科学版), 2012, 37(10):186-1189.
[6]吕志伟,郝金明,曾志林,等. 利用GPS观测资料确定接收机差分码偏差的算法[J]. 全球定位系统, 2010(2):14-17.
[7]MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191-201.
[8]戴连军,唐涛,杨娜. 利用北斗单星三频载波数据估算码偏差的方法[J]. 北京交通大学学报, 2012, 36(2):35-39.
[9]JIN R, JIN S, FENG G. M_DCB: Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J]. GPS solutions, 2012, 16(4): 541-548.
[10]张小红,唐龙. COSMIC低轨卫星GPS接收机差分码偏差估计[J]. 地球物理学报, 2014, 57(2):377-383.
[11]谢益炳,陈俊平,武吉仓,等.不同约束条件对电离层电子含量和硬件延迟的影响[J]. 武汉大学学报(信息科学版), 2014, 39(7):799-803.
AnEstimatingMethodofDifferentialCodeBiasesforBeiDouSatellites
ZHAODongxu,TIPeng,TANShiteng,TANGJian
2015-10-15
长江学者和创新团队发展计划(IRT13092);中央高校基本科研业务费专项资金(2682015CX012)
赵东旭(1993—),男,硕士生,研究方向为大地测量。E-mail:308708931@qq.com
遆鹏
P228
B
0494-0911(2016)05-0014-04
引文格式: 赵东旭,遆鹏,谭诗腾,等. 一种北斗卫星差分码偏差估计方法[J].测绘通报,2016(5):14-17.DOI:10.13474/j.cnki.11-2246.2016.0145.

