基于R-L模型的输电线路阻抗保护的仿真分析

曾燕，张艳华，黄京，郑喻

(三峡大学 电气与新能源学院，湖北　宜昌　443002)



基于R-L模型的输电线路阻抗保护的仿真分析

曾燕，张艳华，黄京，郑喻

(三峡大学 电气与新能源学院，湖北宜昌443002)

输电线路的阻抗保护对于电力系统安全稳定运行具有重要的意义，对输电线路采取了R-L模型的等效方式。R-L模型算法可以不用将非周期分量滤除,所以算法的总时间窗较短；而且它不受电网频率变化的影响，所以在线路距离保护中得到了广泛应用。在simulink中搭建了一典型的输电模型，并在matlab中利用差分方程实现了在线计算线路短路阻抗值，验证了该模型算法的有效性。

R-L模型；距离保护；差分方程；短路阻抗

1　引言

随着现代电力系统的日益复杂,输电线路容量和电压等级不断提高,高压输电线路的保护显得尤为重要，一方面,如果故障测距能够在线完成且精度足够高,对提高系统稳定性、保证系统安全运行有重要的意义；另一方面,准确的线路保护故障定位能够减轻巡线的负担,减小经济损失[1]。

关于线路保护技术的算法，最初有纯正弦函数模型算法，例如最大值算法、半周积分算法、Mann-Morrison导数算法、Prodar-70二阶导数算法和采样值积算法，这些都对波形要求非常严格，一般需要进行预滤波处理[2]。本文采用R-L模型等值输电线路故障处到保护安装处之间的阻抗，利用差分方程实时计算该值大小，并判断该点在直角坐标下是否落在系统线路整定的阻抗圆之内，来鉴定故障是在线路内还是在线路外，算法简单，还分别比较了没有滤波的和加了滤波之后的效果。最后通过实例验证了该模型的可行性。

2　R-L模型和原理

2.1R-L模型原理

由于R-L模型算法忽略分布电容所造成的影响，所以在等效模型中，从故障点到保护处的线路用电阻和电感的串联来表示，则将输电线路等效为简单的R-L模型如图1所示。

其电流电压应满足方程[2]：

(1)

式中R、L为线路段的正序电阻和电感；u、i为保护端的电压和电流。

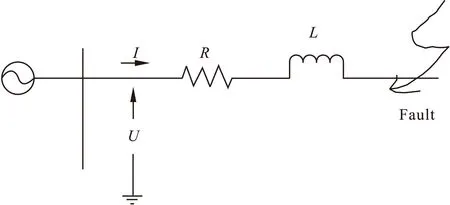
图1　R-L等效图

对(1)式中的微分算式，可以采用差分的方式来计算，需要采样两相连时间的电流和电压，算式如下：

(2)

可以得到：

(3)

其中：

Ts为两采样间隔时间。

为了计算精确，在差分方程中可以利用三个电压电流值来得到两个电压电流的平均值，如下：

2.2R-L模型稳定性分析

由式(3)计算R、L中发现，当分母i2D1-i1D2中两个数较接近时就会失去稳定性，所以需要对影响i2D1-i1D2的因素加以探讨。设电流和其导数都是正弦量：

i1=Imsinα1

D1=Dmsin(α1+αD)

i2=Imsin(α1+θ)

D2=Dmsin(α1+θ+αD)

式中：α1为t1时刻电流的相角；αD为电流的导数超前电流的角度；θ为t2时刻电流滞后t1时刻电流的角度。

进一步有：

即i2D1-i1D2=-ImDmsinθsinαD

可以看出分母值与t1时刻电流的相角α1没有关系，且相间短路时电流导数总是超前电流90°即αd=90°，代入有i2D1-i1D2=-ImDmsinθ。

可见分母i2D1-i1D2的值随着θ值增大而越大，为了提高模型的稳定性，本位采取加大R-L模型中t1与t2时间差的方法以保证模型算法的稳定性。

2.3在MATLAB中R-L模型算法的实现

根据R-L模型算法的原理和差分防长，在MATLAB中编程如图2所示。

图2　R-L算法MATLAB编程

3　滤波器的设计

数字滤波器是具有一定传输选择特性的数字信号处理装置，其输入、输出均为数字信号，实质上是一个由有限精度算法实现的线性时不变离散时间系统；它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换，改变输入序列的频谱或信号波形，让有用频率的信号分量通过而抑制无用的信号分量输出；数字滤波器按单位冲激响应的性质可分为无限长单位冲激响应(IIR)滤波器和有限长单位冲激响应(FIR)滤波器 两种[3]。

为了得到比较稳定变化的电压电流波形，本文采用了巴特沃夫IIR低通数字滤波器，设计参数为：通带频率50Hz，阻带频率60Hz，通带最大衰减1dB，阻带最小衰减60dB，采样频率为140Hz。该算法在matlab中的程序语言如图3所示。

滤波器的幅频及相频图如图4所示。

采样时间间隔为0.02/24s，仿真时间为0.2s，故障时间为0.1～0.2s。

4　实例分析

图5为一500kV输电线路模型，MN为故障线路，NR为非故障线路，故障处距离M端的距离为100km。M、R侧等值系统的参数为：

图3　滤波器编程

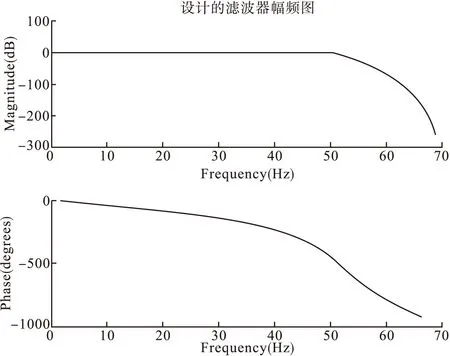
图4　滤波器的幅频特性

ZM=0.66+j16.51Ω

(RM=0.66Ω,LM=52.6×10-3H)

ZR=0.85+j38.5Ω

(RR=0.85Ω,LR=122.6×10-3H)

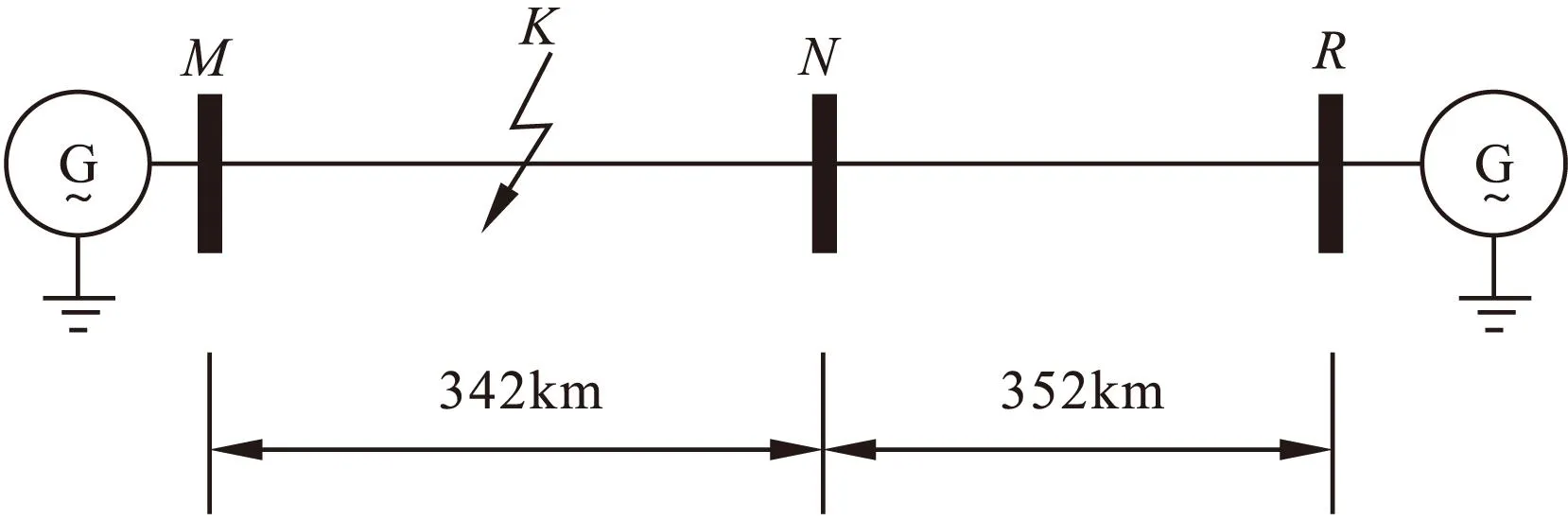
图5　输电线路模型

线路参数为：

正序阻抗：Z1=0.01273+j0.2932Ω/km

R1=0.01273Ω/km,L1=0.9337×10-3H/km；

零序阻抗：

Z0=0.3864+j1.2957Ω/km

R0=0.3864Ω/km,L0=4.1264×10-3H/km；

线路对地正序电容：C1=0.01274μF/km；

线路对地零序电容：C0=0.07751μF/km。

4.1在 simulink中搭建模型

根据图3的系统模型和线路参数，在simulink中搭建模型如图6所示。

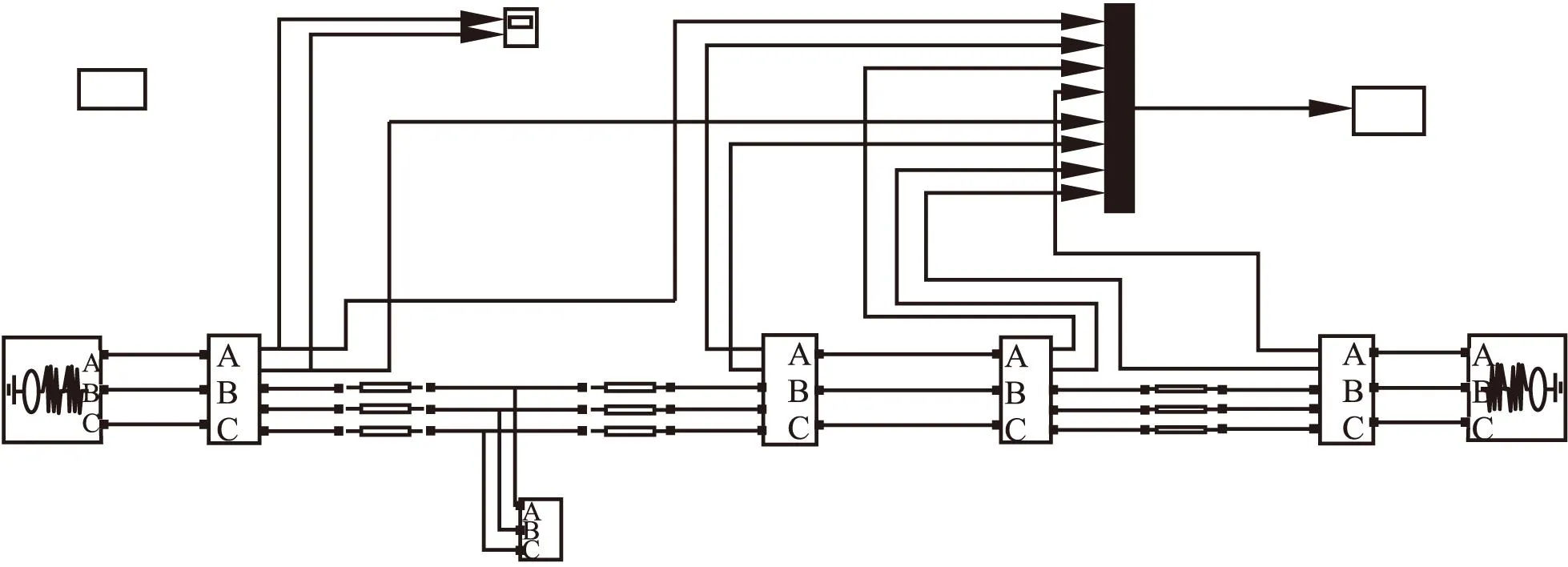
图6　仿真模型

4.2编程仿真

在matlab中通过编程语言实现巴特沃夫低通数字滤波器和R-L模型算法，得到滤波器的幅频及相频图；滤波前和滤波后的电压、电流波形图；线路故障电阻电抗实时图形；阻抗特性圆；测量阻抗值在直角坐标系中的位置。仿真图形如下：

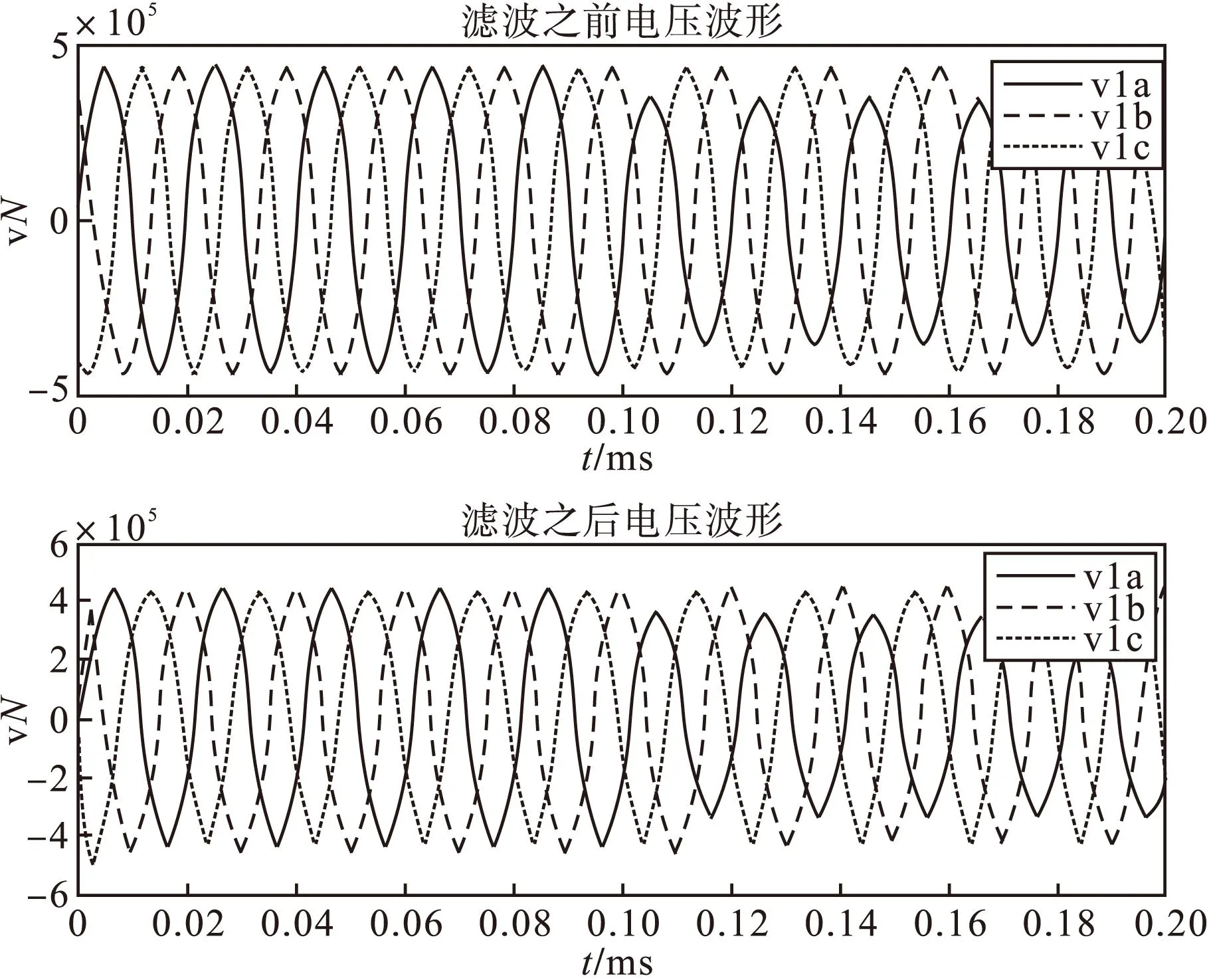
图7　电压波形

以上可以看出故障后故障相电压下降了，而非故障相电压几乎不变。

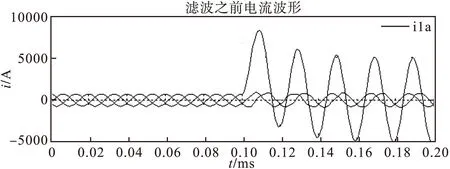
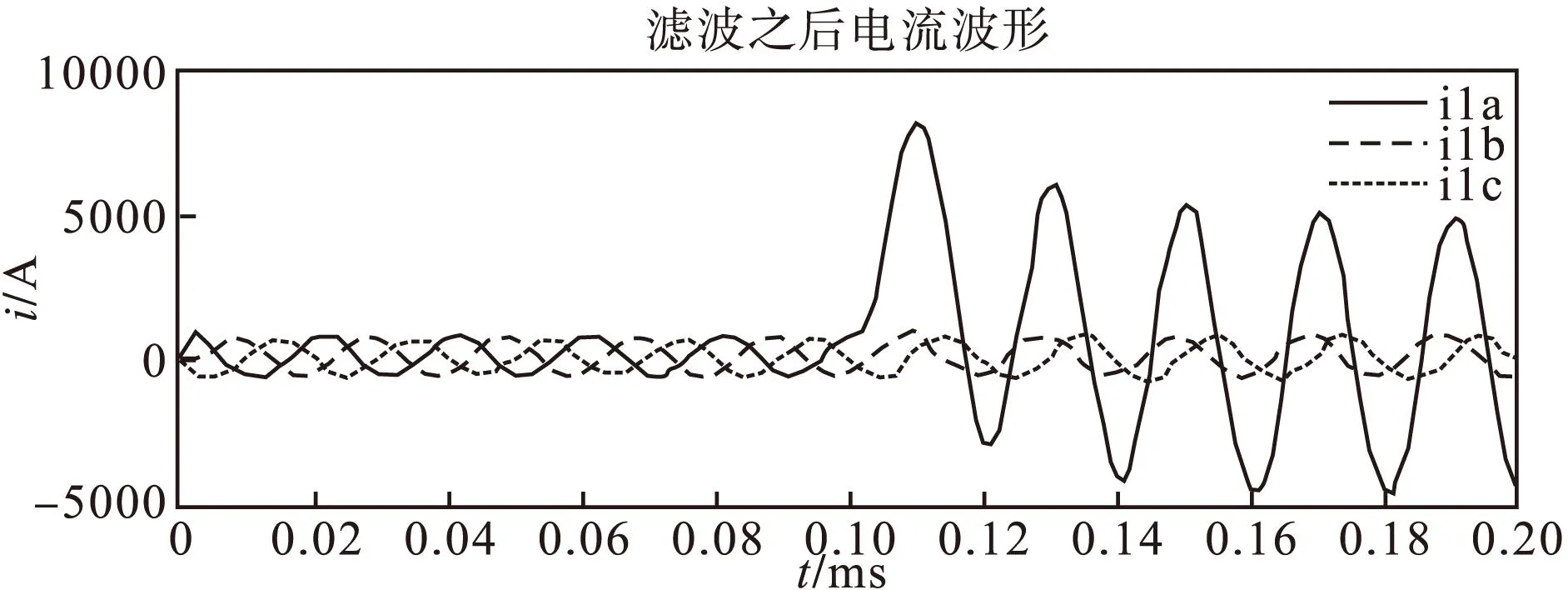
图8　电流波形

故障后故障相电流增大了将近十倍，而非故障相电流几乎不变。

没有经过滤波的故障电阻电抗测量随时间变化的曲线图如图9、图10所示。

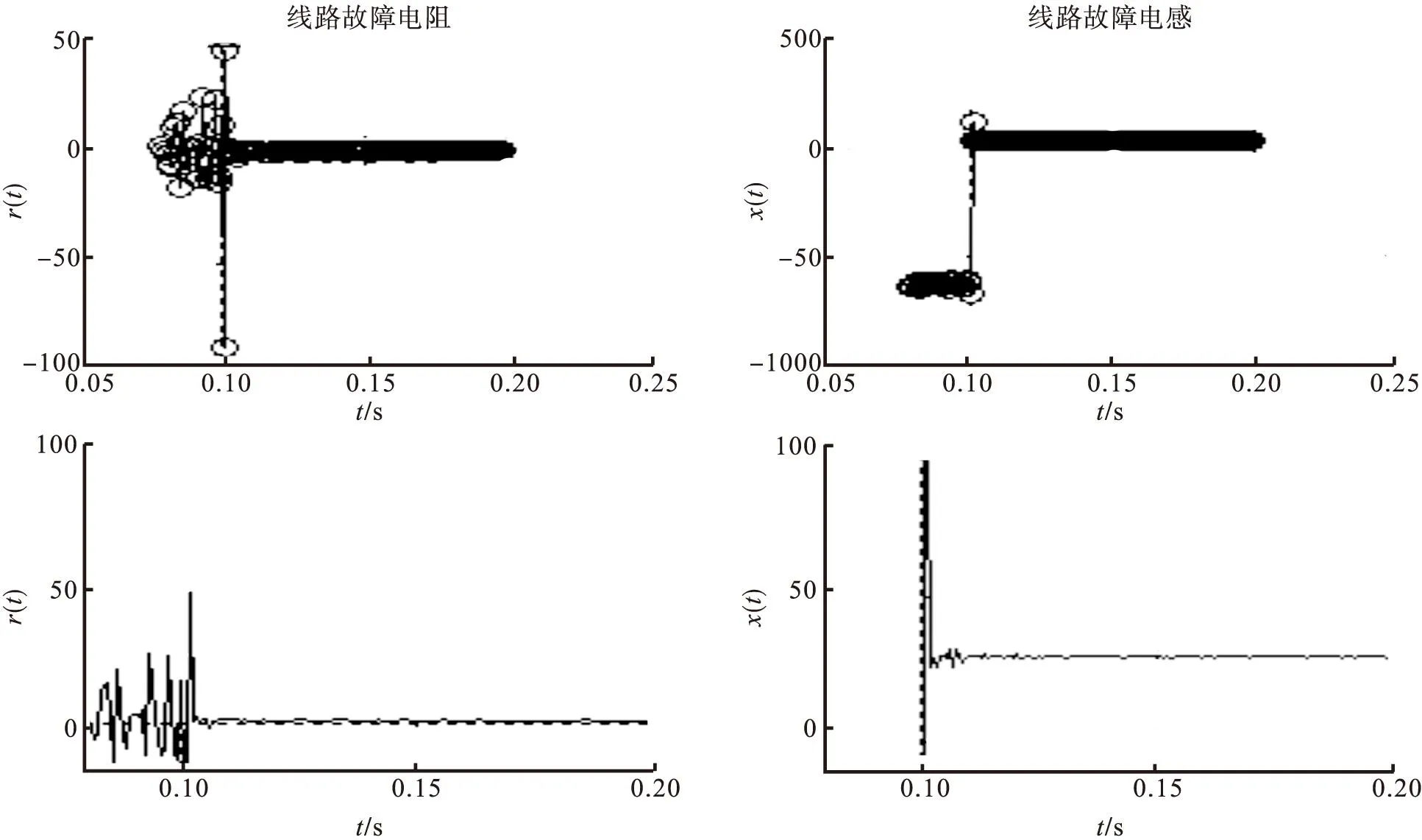
图9　线路电阻与电感随时间变化图及放大图

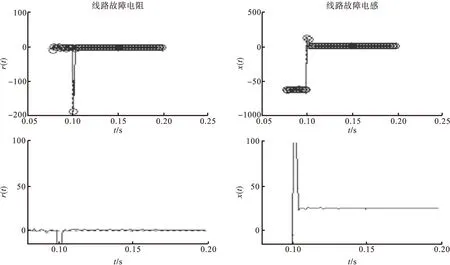
图10　滤波后线路故障电阻、电感时变化图

经过巴特沃夫滤波器后如图11、图12所示。

4.3对线路故障阻抗的测量的分析

通过以上仿真图的分析，得到对线路故障阻抗测量比较分析的结果见表1所示。

由表1可以看出滤波前与滤波之后，测量的故障阻抗值均小于整定值，也就是说该故障发生后，保护能够正常启动，可见R-L模型算法在这里的实用性。但是滤波前测量阻抗误差达到了13.55%，虽然滤波之后阻抗误差稍微减小了，但误差还是较大，又见此算法还需要继续优化。

表1

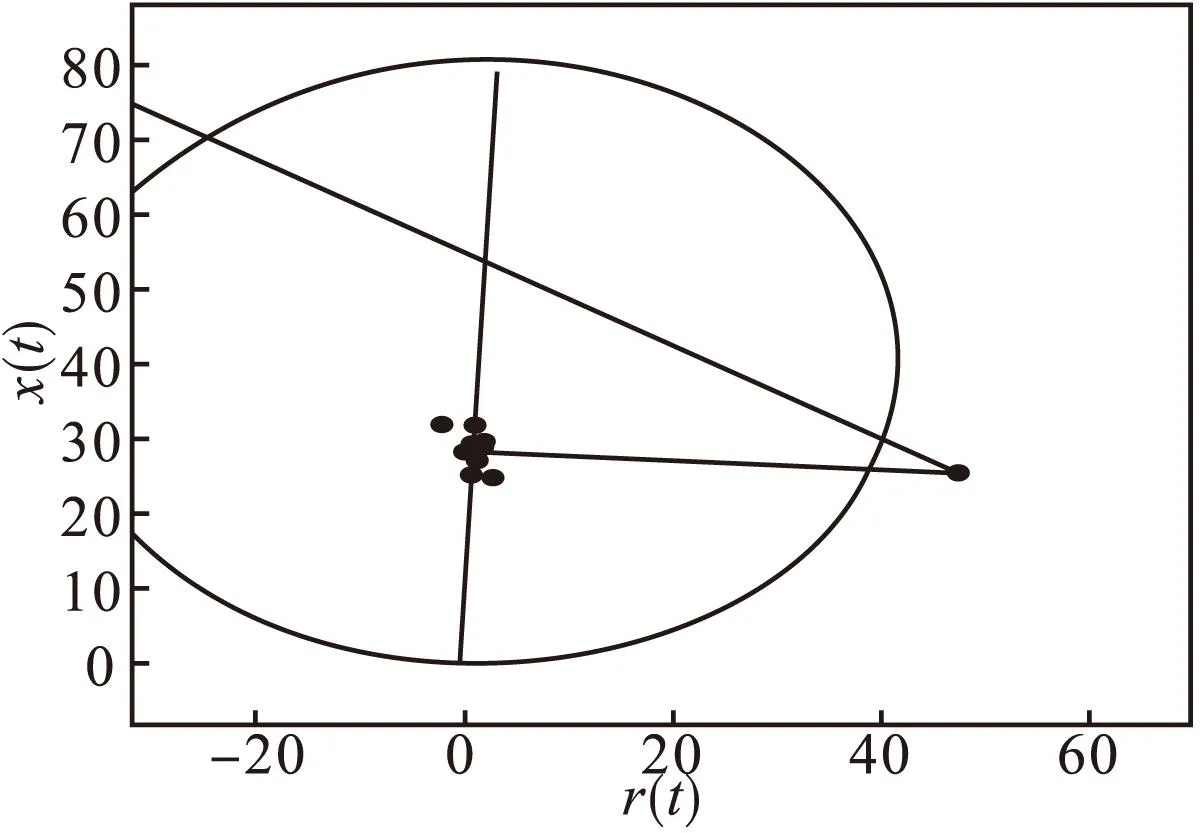
图11　滤波前的阻抗落点图

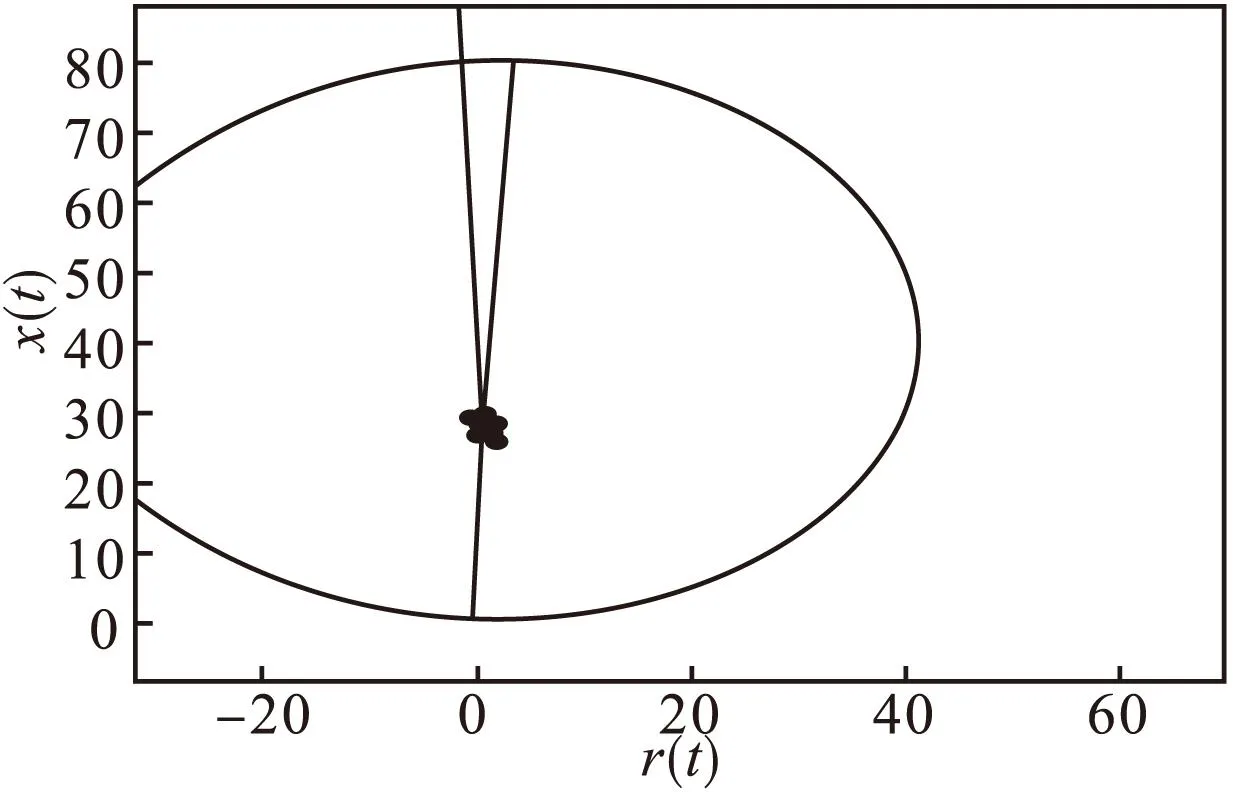
图12　滤波后的阻抗落点图

5　结论

通过理论分析和实例仿真,得到以下结论:

(1)通过仿真可以看到,利在短路情况下,线路分布电容主要体现为高频分量,故采用低通滤波器滤除高频分量后,R-L模型算法仍有其适用性，用模型微分直接求解法的阻抗继电器动作迅速,数据窗短,可作为一段距离保护元件使用。

(2)用差分替代一阶与二阶微分；将模型简化，清晰明了。

(3)通过以上单相接地故障的仿真，可见R-L模型在线路故障阻抗保护中具有一定的实用性，该算法简单，便于操作，适用于一般对保护要求不高的线路。

[1]索南加乐,齐军,陈福锋,等.基于R-L模型参数辨识的输电线路准确故障测距算法[J].中国电机工程学报，2004，24(12)：119-125.

[2]韩奕.微网及含分布式发电的配电网保护算法研究[D].中国电力科学研究院,2011.

[3]陈明，张涛.基于R-L模型算法的距离保护研究与PSCAD仿真[J].电力学报，2010,25(2)：167-170.

[4]周耀辉,王芸波,朱维新,等.IIR数字滤波器设计[J].电力自动化设备,2010,30(9)：129-131.

Simulation Analysis of Transmission Line Resistance Protection Based on R-L Model

ZENG Yan，ZHANG Yan-hua，HUANG Jing，ZHENG Yu

(China Three Gorges University，Yichang 443002，China)

The resistance protection of the transmission lines is of great significance to the safe and stable operation of the power system,this paper adopts the R-L model as the equivalent of transmission lines.The total time of the R-L algorithm is relatively short since the aperiodic component can not be filtered,and it can′t be affected by changes in frequency,so it is widely used in line distance protection.This paper built a typical transmission model in Simulink,and realize the online calculation of short circuit resistance value in the MATLAB by using differential equations,which verify the effectiveness of the R-L model algorithm.

R-L model;distance protection;differential equations;short circuit resistance

1004-289X(2016)01-0041-04

TM72

B

2015-04-27

曾燕(1988-)，女，硕士研究生，研究方向：继电保护。