基于粒子群优化算法的永磁同步电机参数辨识

丁金多

(东北电力大学，吉林　吉林　132012)



基于粒子群优化算法的永磁同步电机参数辨识

丁金多

(东北电力大学，吉林吉林132012)

提出了一种对永磁同步电机的直轴电感、交轴电感和定子电阻进行辨识的粒子群优化(PSO)算法。该算法具有快速、稳定的收敛性,不需要电压源逆变器和闭环控制策略，容易实现。通过PSO算法的实验结果，证明了PSO算法的有效性。

参数辨识；粒子群优化(PSO)；永磁同步电机(PMSM)

1　引言

永磁同步电机具有结构简单、体积小、效率高、功率密度高、响应速度快和安全性高等诸多优点，因此通常将永磁同步电机应用于矢量控制中。这些控制需要精确的电机参数,如定子电阻、电感,转子永磁体磁链等。然而，由于制造商通常只提供少数电机的参数，主要是因为参数随着温度和磁饱和程度的变化而变化。因此，辨识永磁同步电机的参数变得十分必要。参数的辨识可以分为在线辨识和离线辨识。在线辨识技术常用于自适应系统的控制和预测。目前已经用于在线参数辨识的方法有，扩展卡尔曼滤波(EKF)[1-2]，模型参考自适应[3]和递归最小二乘法(RLS)[4]；离线辨识技术是一种更适合密集计算的方法，可分为实验性的，如电流衰减测试法(CDT)[5]，注入不同交流波形法[6]，停顿频率响应(SSFR)测试法[7]等。计算性的有，如进化算法，粒子群算法(PSO)[8]，神经网络法(NN)[9]等。

由于在线辨识通常应用于电机运行时，所以只可以辨识少数的参数，而且准确的在线辨识需要电压源逆变器、快速的数字化平台和矢量控制策略，从而增加了辨识的成本和实施的复杂性。为此，本文提出了一种离线辨识法，即运用粒子群优化算法对永磁同步电机进行参数辨识。所提出的PSO算法的主要优点是它的快速收敛性，良好的辨识精度，且易于数字实现。同时辨识过程既不需要电压源逆变器，也不需要矢量控制策略。

2　永磁体磁链和定子电组的实验测定

2.1数学模型

永磁同步电机dq轴坐标电压方程和磁链方程：

(1)

ψq=Lq(iq)iq

(2)

(3)

ψd=Ld(id)idψf

(4)

其中，vd和vq为d、q轴的电压分量，ψd,ψq为定子磁链d轴分量；q轴分量，ωr为转子旋转角速度，Ld(id)和Lq(iq)为d、q坐标系下的自感系数，该参数分别为id和iq的函数；Rs为定子电阻；ψf为永磁发电机转子磁链。电磁转矩Te为；

(5)

其中p为永磁发电机极对数。B为为粘滞摩擦系数。ω为机械角速度，TL为负载转矩，J为转动惯量。

2.2永磁同步电机磁链的测定

永磁同步电机的转子磁场是由永磁体产生的，磁链ψf在测试过程中不需要加入负载就可以直接测量，其测量原理为：

因电机的电角速度ωe为：

ωe=2πpn/60

(6)

其中：p为电机的极对数，n为电机转速。

电机的电压：

U=ψf×ωe

(7)

通过上述分析可以得到ψf的表达式：

ψf=U/ωe

(8)

2.3定子电阻Rs的测定

电机的相电阻采用直流伏安法进行测量，其测试的原理如图1所示。

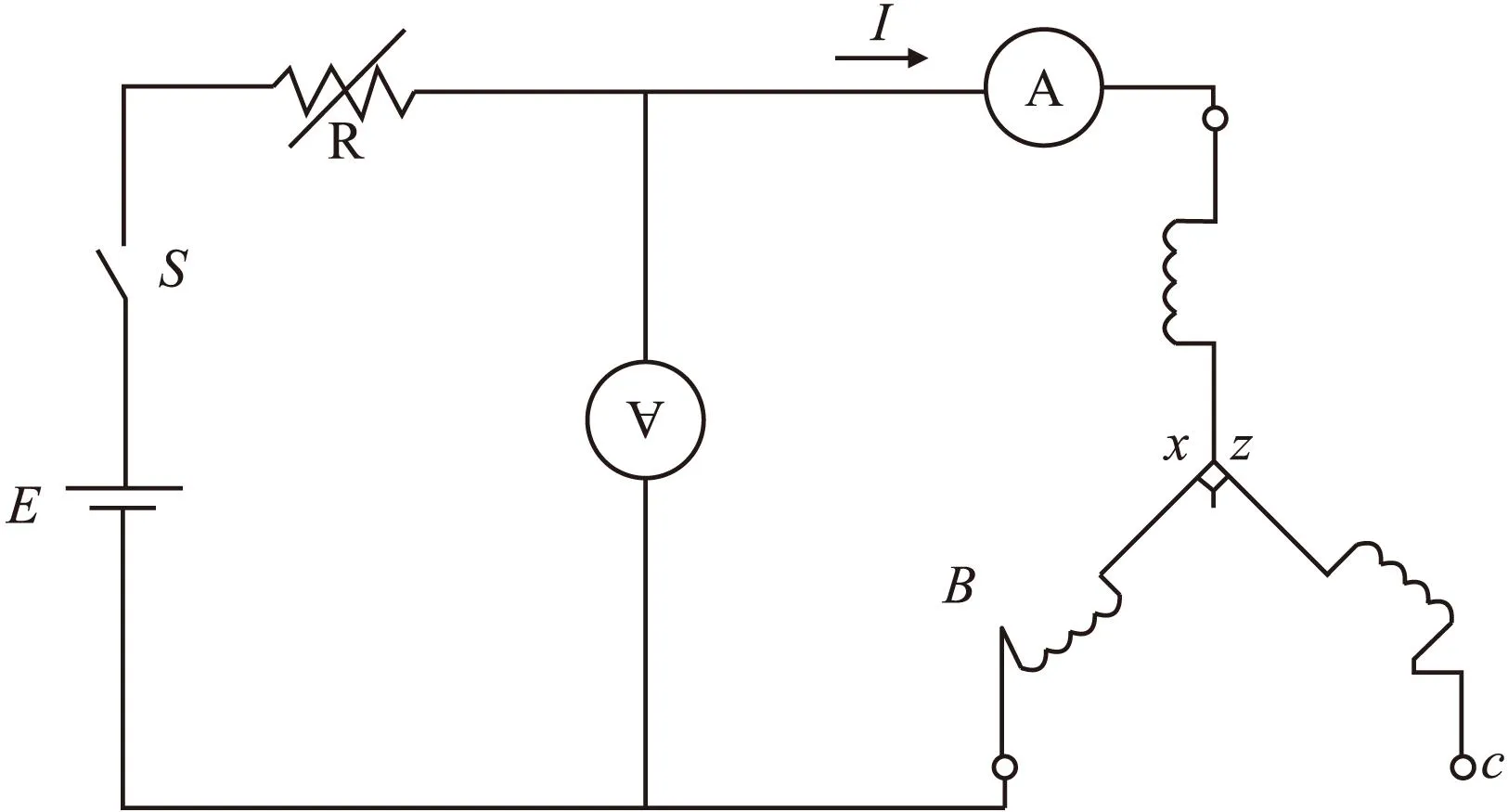
图1　采用直流伏安法测量相电阻原理图

连接电路如图所示:

R1=RA+RB

(9)

R2=RC+RB

(10)

R3=RA+RC

(11)

一般电机三相的相电阻RA=RB=RC，因此采用直流伏安法测得的电机定子的电阻值为：

(12)

3　PSO算法对定子电阻和定子电感的辨识

3.1粒子群优化算法

粒子群算法由Eberhart 和Kennedy提出的通过模拟鸟群觅食过程中的迁徙和群居行为而提出的一种群体智能的全局随机搜索方法。通过个体间的协作与竞争，实现复杂空间最优解的搜索。每一个粒子随机分布在搜索空间中，并且会记忆在空间中找到的最优算法的位置。根据最优算法的位置，调节所有粒子的位置和速度。每个粒子由位置矢量和速度矢量组成，在k时刻分别给定；

(13)

(14)

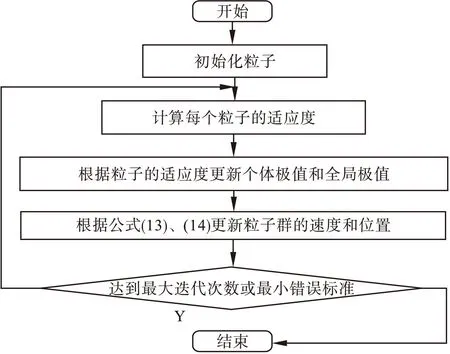
图2　PSO算法流程图

3.2交流法的测试原理

定子电感Ld(id)和Lq(iq)是id和iq的函数，因此，电感通过对不同的电流进行估算获得。如图3所示，当转子d与轴轴线一致时，式(1)可以简化为：

(15)

将式(15)离散化，得到k时刻的定子电流id为：

(16)

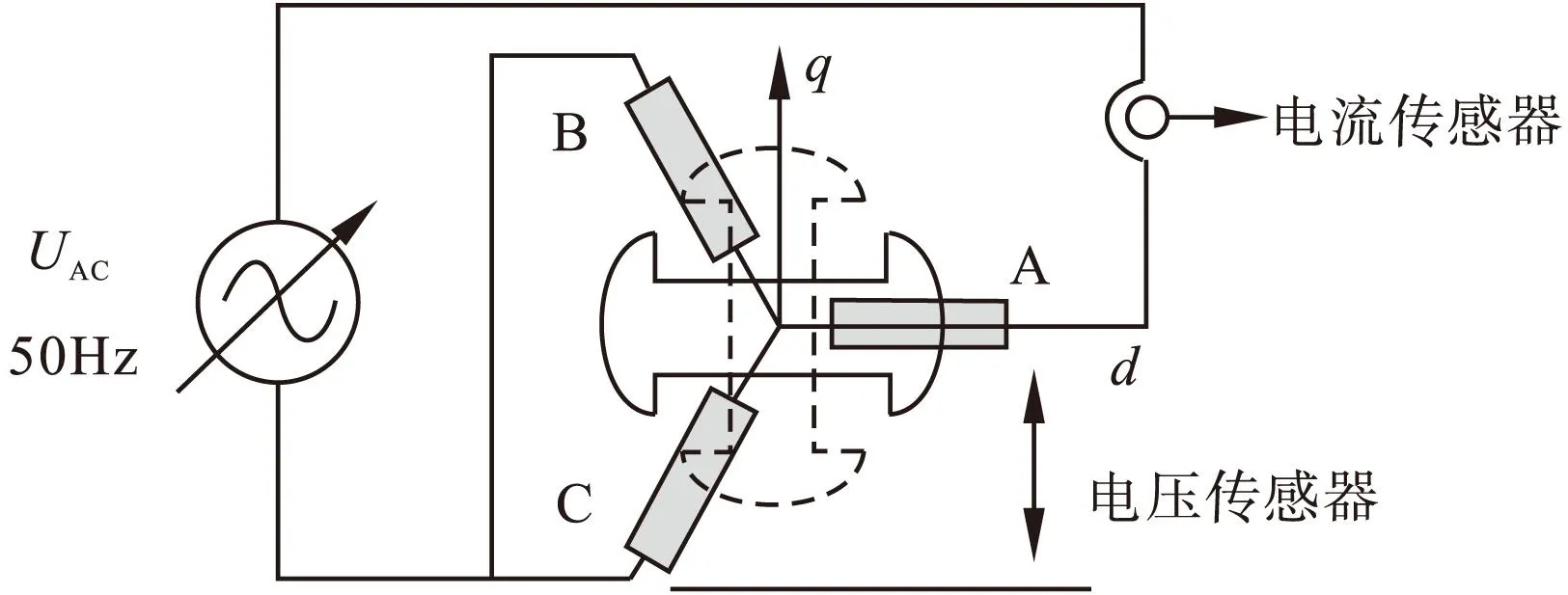
图3　PSO算法辨识电感Ld,Lq的原理图

3.3目标函数

参数辨识可以作为系统响应于一个已知输入来获得模型未知参数的优化问题。为了获得更好的准确性,在输入的激励信号与实际的激励信号一致时，确认模型响应与系统响应相似。基本思想是基于一个被最小化且定义系统响应与模型响应相似的价值函数，来比较系统响应与参数化模型响应。为了实现PSO算法对参数的辨识，当定子电流和定子电压已知时，提出了一个优化函数，可以成：

id(k)=Δt[χ1ud(k-1)-χ2id(k-1)]+id(k-1)

(17)

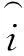
(18)

n表示样本数，电感Ld(id)和电流Rs的值通过探索解空间以及接近PMSM动态特性来进行迭代调整。利用相同的方法对电感Lq(iq)进行辨识。

3.4粒子群优化算法的收敛性

粒子群优化算法的随机性导致系统很难收敛到全局或局部最小值。然而，PSO算法的收敛性取决于惯性系数及加速度的选择，由此可以得出该算法的收敛性。为了证明收敛性，由于在粒子群中的不同尺寸粒子之间没有相互作用，因此可以简化分析单个粒子，假设其余部分的粒子是静止的。利用这种方法，通过非齐次递推关系可以得到:

ai(k+1)=(1+ω-φ1+φ2)ai(k)-ωai(k-1)+φ1api+φ2ag

(19)

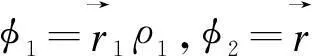
ai(k)=k1+k2αk+k3βkω

(20)

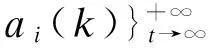
(21)

其中t=ρ2/ρ1+ρ2,因此t∈[0,1]。等式(21)显示,粒子收敛于个体最优与全局最优的某个线性组合点，它表明了粒子将搜索位于它的个体最优与全局最优之间的具有更好解的区域。进一步的分析可得到，当ρ1,ρ2,ω满足关系时，能够得到粒子收敛轨迹。

(22)

4　PSO算法辨识的仿真结果

采用PSO算法辨识定子电感，在短时间内，将电机的定子绕组按(图3)与电源连接，测量电机的电流和电压。对于PSO算法必要的参数有：群体规模，最大遗传代数，加速度和惯性系数。

图4显示了采用PSO算法对电流进行优化，在迭代过程中，电流最优曲线根据电流测量曲线进行调整。图4(a)表示在第一次迭代时的电流曲线；图4(b)和4(c)表示在第10次和35次迭代时的电流曲线。观察最优电流与测量电流是否匹配。当第35次迭代时，测量电流和最优电流之间的误差足够小时，则可以确定电机的参数。

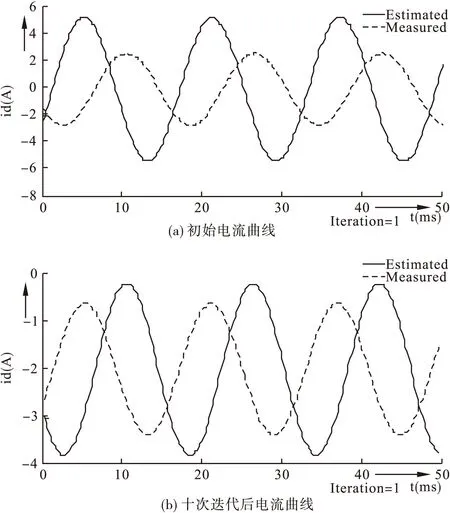
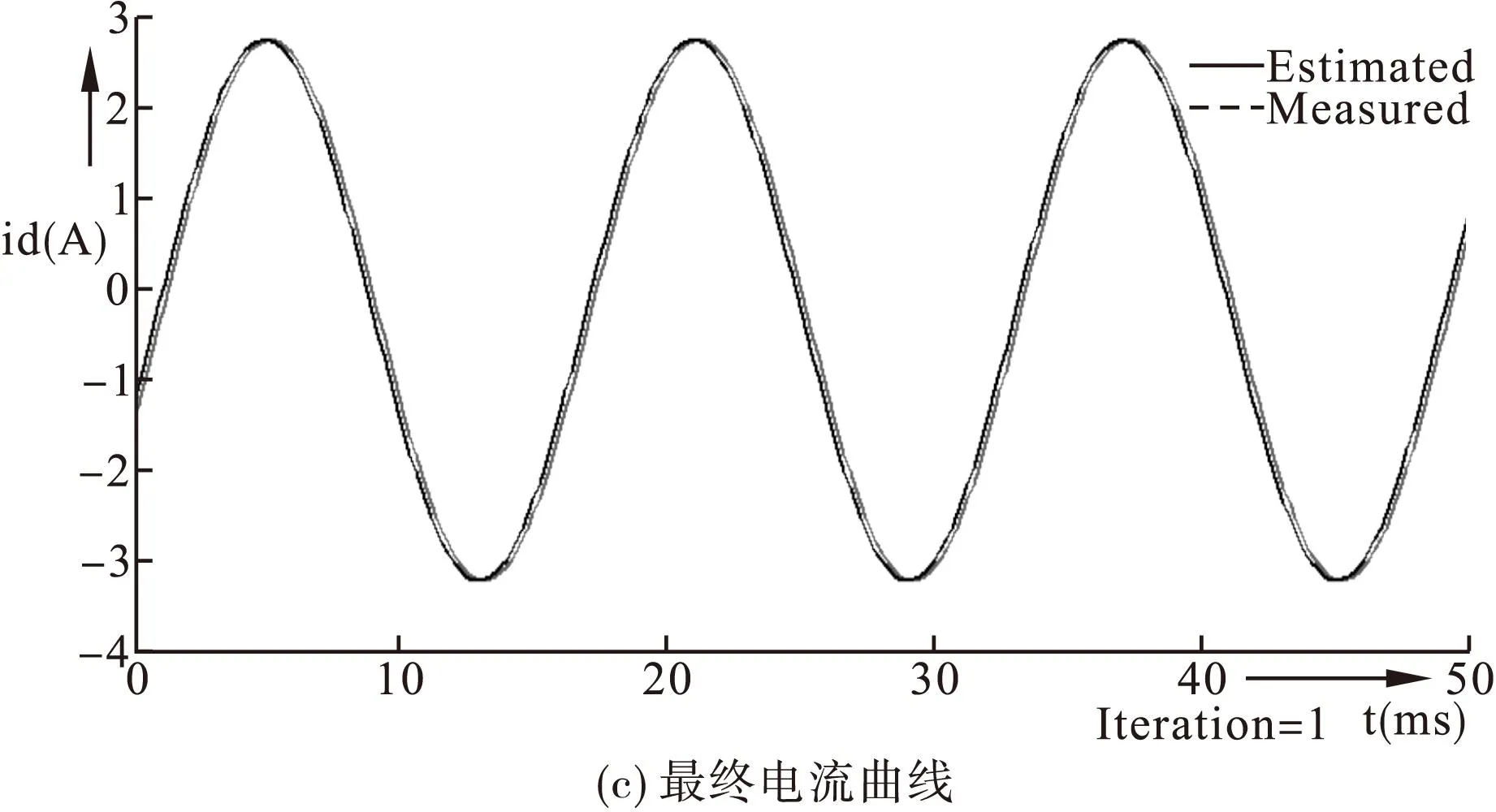
图4　利用PSO算法对电流曲线进行优化

图5显示了所获得的粒子轨迹的收敛性与所选择的惯性系数和加速度值之间的关系。由图5可见，振荡的振幅随着时间变化而衰减。这表示粒子半径的搜索模式变为空间搜索；最初的粒子探索范围较大，但当粒子探索的邻域接近全局最小值时，振幅迅速下降。图6显示利用PSO算法对电感进行辨识。由于测试的电机是面贴式永磁同步电机，所以最终交直轴电感的值接近。图7显示对定子电阻的辨识。与电感调节相似，电阻在35次迭代后保持稳定。

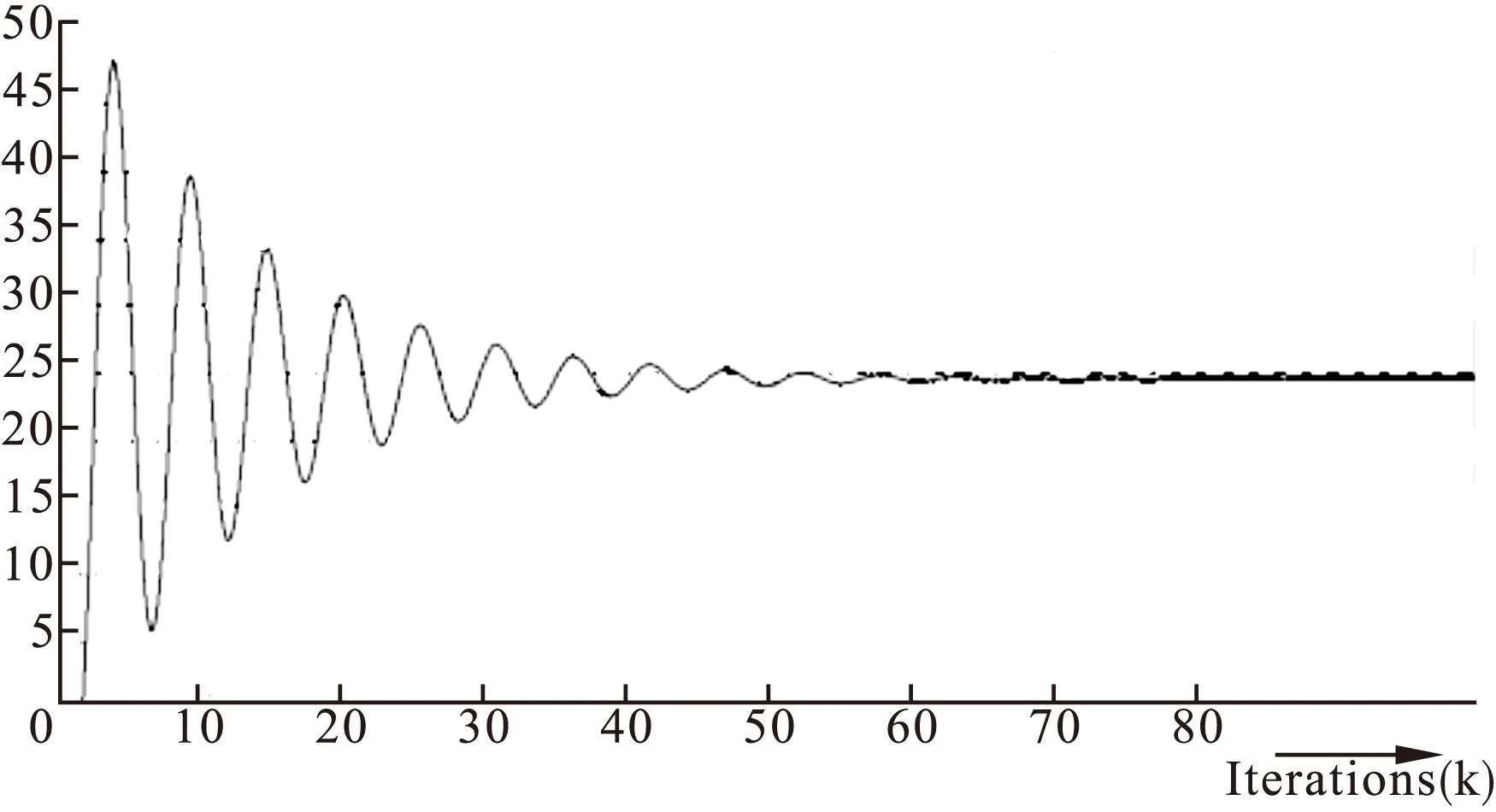
图5　粒子轨迹的收敛性

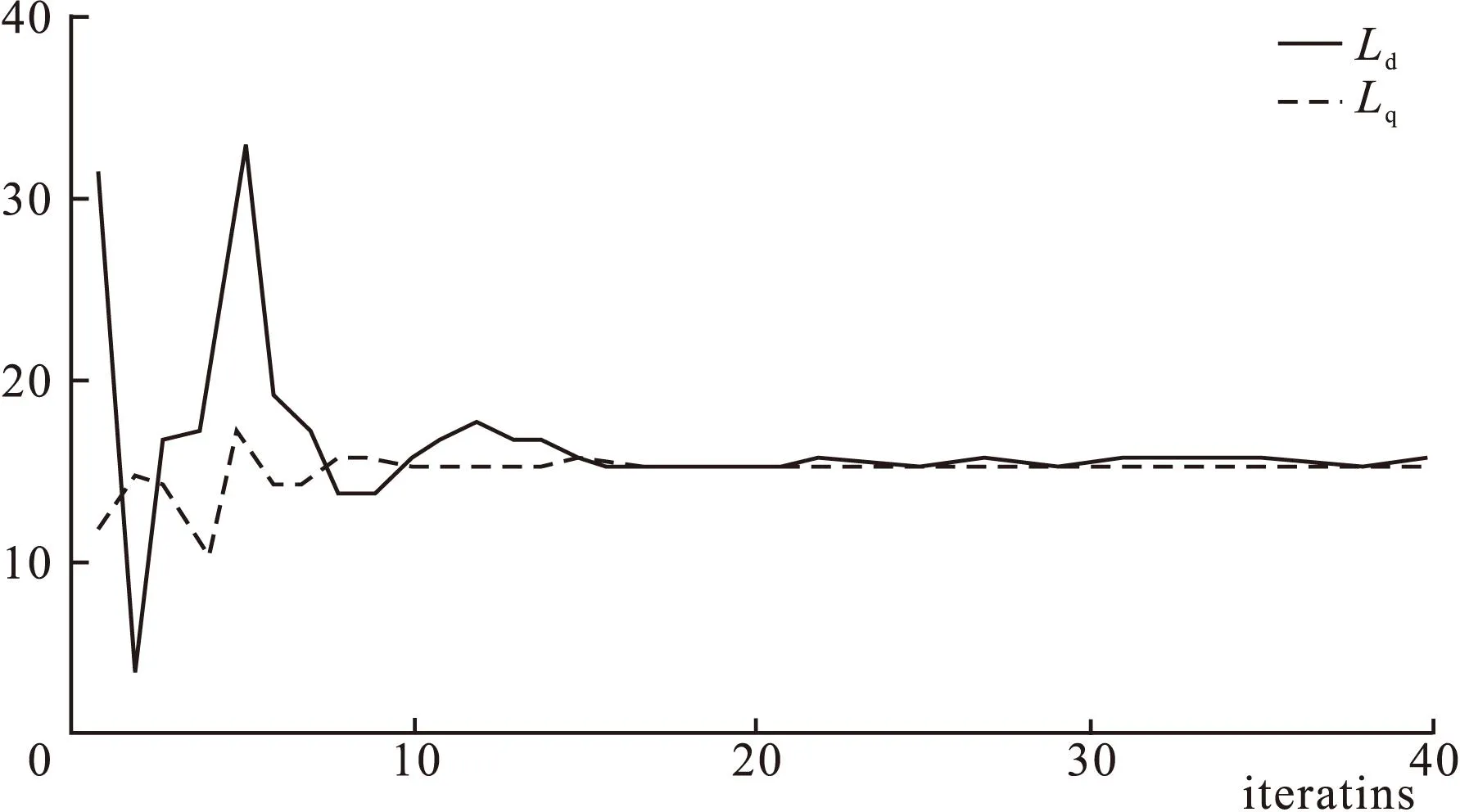
图6　PSO算法对Ld,Lq参数的辨识结果

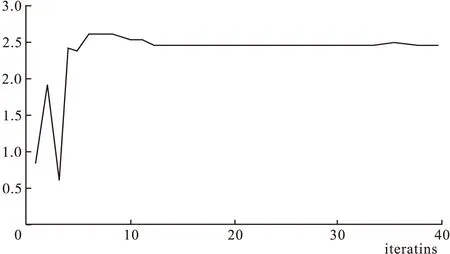
图7　PSO算法对Rs辨识结果

Lq(mH)Lds2(Ld)Lq(mH)Lqs2(Lq)28.59040.003184426.18920.002485626.26750.002748025.66030.002859925.81950.002652325.99630.002087025.31020.002335424.77970.002279128.87990.002035924.69010.0025065

5　结论

本文中，运用PSO算法对永磁同步电机交直轴电感进行辨识，并且通过仿真进行了验证。PSO算法可以对定子电阻，交直轴电感进行同步辨识。对该算法的收敛性、不确定性及鲁棒性进行了验证。同时证明了PSO算法辨识的有效性。

[1]王松,刘明光,石双双,等.基于卡尔曼滤波和神经网络的 PMSM 参数辨识[J].北京交通大学学报,2010,34(2):124-127.

[2]王磊，李宏，武明珠，等.基于扩展卡尔曼滤波的永磁同步电机参数辨识[J].微特电机，2012，40(7):60-67.

[3]邵友，陈国定.永磁同步电机的变结构MRAS 转速辨识[J].2012,45(10):53-55.

[4]张洪东，李宏，郑勇.基于递推最小二乘法的永磁同步电动机参数辨识[J]，微特电机，2011(11)：14,16.

[5]向纯靖，李长兵.基于最小二乘法的永磁同步电机参数辨识[J]，微特电机，2012，40(2)：30-34.

[6]L.Shen,J.Wu,S.Yang,and X.Huang,“Fast flux linkage measurement for switched reluctance motors excluding rotor clamping devices and position sensors,”IEEE Trans.Instrum.Meas,2013,62(1):185-191.

[7]M.Cisneros-Gonzalez,C.Hernandez,R.Morales-Caporal,E.Bonilla-Huerta,and M.A.Arjona,“Parameter estimation of a synchronous-generator two-axis model based on the standstill chirp test,”IEEE Trans.Energy Convers,2013,28(1):44-51.

[8]Z-H.Liu,J.Zhang,S-W.Zhou,et al.“Coevolutionary particle swarm optimization using AIS and its application in multiparameter estimation of PMSM,”IEEE Trans.Cybern,2013,43(6):1921-1935.

[9]L.Kan,Z.Qiao,C.Jintao,et al.“Online multiprameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking,”IEEE Trans.Ind.Electron,2011,58(5):1776-1788.

Parameter Identification of PMSM Based on a PSO Algorithm

DING Jin-duo

(Northeast Power University，Jilin 132012,China)

This paper introduces a particle swarm optimization(PSO)algorithm for the identification of the direct(d)and quadrature(q)stator inductances and the stator resistance of permanent-magnet synchronous machines.The developed PSO algorithm has the advantages of fast and stable convergence characteristics,and it is relatively easy to implement;moreover,neither voltage source inverters nor closed-loop control strategies are needed.In this paper,the experimental results obtained by PSO demonstrate the effectiveness of the presented method.

parameter identification；particle swarm optimization(PSO)；permanent magnet synchronous machine(PMSM)

1004-289X(2016)01-0034-05

TM341

B

2015-06-10

丁金多(1989-)，男，东北电力大学硕士研究生，研究方向：永磁同步电机参数辨识。