物流服务提供商关系协调的博弈分析
■ 程 静 副教授(西安外事学院商学院 西安 710077)
物流服务提供商关系协调的博弈分析
■ 程静副教授(西安外事学院商学院西安710077)
内容摘要:本文应用博弈分析理论对物流服务商之间的合作进行研究,分成合作配送和不合作配送两种情况进行讨论。研究发现,合作配送可以增加物流服务商的利润。文章采用纳什讨价还价模型得到最优转移价格,实现物流服务商之间利润协调,并进行数值模拟对研究结果进行验证。
关键词:博弈纳什讨价还价模型物流服务提供商协调
目前,国内快递行业处于低价无序竞争状态,服务商依赖低价来确保竞争优势。为了维持低价,很多物流服务提供商之间开始形成合作联盟。因此,从理论角度对物流服务提供商的配送战略包括服务价格、配送范围、合作配送进行相关研究是非常有必要的。
模型构建
(一)模型描述
假设用两个同心圆来描述整个需求区域,两家物流服务提供商A和B的配送中心位于同心圆的圆心。另外,将整个地区看作圆心,而其他地区看作是圆圈,配送中心到内圆边界,也就是内圆的半径为1,而外圆的半径为d,正如顺丰速运的价格策略,在这两个区域的服务价格是一样的。消费者均匀地分布在两个圆的边界上,其中内圈的消费者数量为N1,外圈的消费者数量为N2。但是,消费者对不同的配送速度具有不同的偏好。根据有关消费者偏好的设定,假设消费者关于配送速度的偏好为θ,并且服从0到1的均匀分布。该偏好值越大,消费者越倾向于选择水平高的服务。每一个消费者在选择这两个物流服务提供商的服务时,可以得到的效用分别为UA和UB,消费者会选择能够带来较高效用的物流服务。根据效用模型,发现需求竞争的结果与配送速度有关,据此分成新提供较快配送速度与较慢配送速度两种情况来讨论。
(二)模型假设
本文在进行博弈分析时,做出如下假设:假设物流服务企业参与合作配送的只有快递企业A和快递企业B,企业的博弈策略只有合作和不合作;整个需求地区分为n个小区域,这些区域是相互独立的,有无数个需求点,为了简便计算,选取每个区域的一个核心点来代替整个区域来进行成本核算;本文只考虑物流服务提供商的配送成本,而忽略了折旧、库存成本、管理成本、财务成本、其他工人的工资;每一个包裹的重量、形状和费用是一样的;每一个物流服务提供商拥有足够的能力来满足配送需求;合作配送不考虑配送时间。物流企业之间的博弈策略组合见表1。
(三)模型符号
为了更好的阐述博弈关系,本文中所用到的主要参数及符号如下:pi消费者向物流服务提供商i支付的配送费用;vi物流服务提供商的配送速度;qij需求区域j对物流服务提供商i的需求量,j=1,…,n;Qj需求区域j的总需求,j=1,…,n;Cij物流服务提供商i在需求区域j的单位配送成本,j=1,…,n;qj物流服务提供商1在需求区域j帮助物流服务提供商2配送的业务量;ct单位转运包裹的转运费用;∏n非合作情况下两个物流服务提供商的总利润;∏0合作情况下两个物流服务提供商的总利润;p向合作伙伴支付的单位包裹的转运价格。
(四)模型博弈效应分析
1.不合作配送。首先分析在业务获取阶段,两个物流服务提供商之间的竞争关系。网络零售商向消费者出售同一种产品,由于网络销售的本质是零售商与消费者空间上的分离,因此,零售商需要依赖物流服务提供商提供配送服务来完成整个交易,而消费者在得到产品之前需要等待一定的时间。两个物流服务提供商提供配送速度,并且对每一次配送服务收取费用,以此来获取相应的竞争优势。此时,假设物流服务提供商A的配货速度较快,配送费用较高,物流服务提供商B的配送速度较慢,配送费用较低,即vA-vB>0,pA>pB。物流服务提供商的利润函数如下:

物流服务提供商A需求区域j需求为:

物流服务提供商B需求区域j的需求为:

联立(1)、(2)、(3),物流服务提供商A利润函数为:

物流服务提供商B的利润函数为:

求解公式(4)和公式(5)的一阶偏导数和二阶偏导数,得到物流服务提供商A的价格反应函数:

物流服务提供商B的最优的价格反应函数:

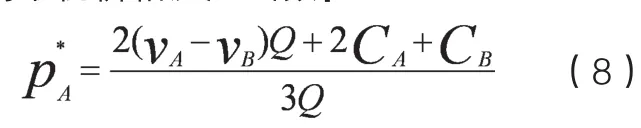
物流服务提供商B的最优价格反应函数:

由上述的最优价格以及相应的需求量,两个物流服务提供商在不合作的情况下,所能获得的总利润可以表示为:

2.合作配送。合作博弈指物流服务提供商进行合作,将二者构成的物流服务供应链看做一个集成的系统,也就是联合决定物流服务配送价格和配送数量使得系统利润最大化。在以上博弈模型基础上,为促成博弈双方进一步合作,实行区域集中控制。在提升物流服务提供商整体绩效的同时,也使他们各自利益增加,运用收益共享契约进行协调,从整体利益最大化角度确定配送距离和范围。一个物流服务提供商可以利用该契约引导另一个服务提供商进行配送阶段的合作,以此来获得更高的利润。如果两者合作,那么两者的总利润是最大的,也就是说该契约能够达到协调的目的。供应链各个成员企业都以供应链整体的利益最大为目标,整个供应链就像一家企业,从而消除了供应链内部之间的交易成本。以最大化总系统利润为目标选择最优合作分配策略。决策变量为市场需求和市场价格。
设定物流服务的单位配送成本:

公式(11)中,αi和β的取值范围为0-1,在相同配送距离的前提下,较快的配送速度会带来较高的配送成本。因此,根据vA>vB,可以设定αA>αB,物流服务提供商相互合作配送。假设服务提供商A帮助提供商B在需求区域j配送qj个包裹,整合的物流服务提供商需要决定qj来获得最大利润:

合作配送会带来一定的转运成本Ct。设定:采用基于单位货物转移价格的转移支付机制来达到协调。单位货物转移价格为P,转移价格通过纳什讨价还价策略决定,两个物流服务提供商的议价能力分别为λA、λB,取值范围在0-1之间(包含0和1),
则物流服务提供商B需要向物流服务提供商A支付的费用为:

利润增加值的函数为:

对于两个物流服务提供商而言,利润值为:

(五)数值仿真
为了验证所提出的模型的正确性,对服务商上述协调共享情况进行数值仿真,赋值情况为:市场的基础需求量j为100.0,物流企业A配送成本cA为2.0,物流企业B配送成本cB为3.0,单位包裹中转费用ct为1.5。
以0.01为步长变动,设定a=0.41,b=0.59;a=0.43,b=0.57;a=0.45,b=0.55;a=0.47,b=0.53;a=0.49,b=0.51;a=0.51,b=0.49;a=0.53,b=0.47;a=0.55,b=0.45,求得a、b取不同值下各个决策量及最优利润,并使用Matlab作出函数图,结果如图1和图2所示。
图1和图2反映了讨价还价能力对物流服务企业各自利润函数的影响。从中可以看出,在不合作配送条件下,物流服务提供商A与B的利润并未随讨价还价系数的提升而发生变化,而是处于基本平稳不变的趋势。但是在合作配送条件下,物流服务提供商A与B的利润则随着讨价还价系数的提高而表现出不断上升趋势,并在达到一定系数后上升趋势趋于平缓。这说明加强物流服务商之间的合作可以有效提升物流服务商双方的利润,合作配送是将来物流业发展的一个重要方向。

图1 讨价还价系数对物流服务提供商A利润的影响

图2 讨价还价系数对物流服务提供商B利润的影响

表1 不同物流服务企业之间的博弈组合策略
物流服务商关系协调策略
第一,转变目标模式。目前,我国物流金融业务模式依旧停留在传统模式上,物流金融风险较大,应将物流服务与金融服务相结合进行业务模式创新,研究金融业与物流业的协同发展,使物流行业降低成本,提高效益,扩展物流企业的业务范围,推动行业转型升级,提升其在市场中的竞争地位。
第二,强化物流运行模式,充分体现物流的本质。“整合资源、优化流程”,这是物流永恒的主题。只有在整合资源基础上优化流程,才能够提高效率,才能够达到降低成本的目标。这是物流领域在应用互联网时所必须要强化的。
第三,提升物流组织模式。互联网对于物流发展最大的推动力之一就是加快物流组织模式尽快向供应链转型升级。就是要企业和企业之间,或者一个产业链平台上,基于“互联网+”进行资源整合和优化,建立供应链成员企业间统一的战略目标和企业文化,增强自身竞争力,建立可信任形象。“互联网+”物流服务供应链以能力合作为核心实现了供应链成员之间的利润合理分配,提高了整个物流服务供应链运营绩效。
第四,创新物流发展模式。新时期的物流行业竞争必然离不开大数据,在大数据下实现多方物流服务提供商的合作共赢。因此,未来物流服务商之间应在数据分享及信息共享的基础上大力支持合作伙伴的发展,创新物流发展模式,在成员企业间建立多种沟通渠道,为物流服务商之间的合作配送创作良好的外部条件。
参考文献:
1.范如国.博弈论[M].武汉大学出版社,2011
2.陆春华.基于多周期合作的物流服务供应链质量协调分析[J].商业经济研究,2016(1)
3.张文洲.促销视角下在线零售商和物流提供商的供应链协调研究[J].商业经济研究,2015(9)
中图分类号:◆F252.3
文献标识码:A

