组块3×2交叉验证的F1度量的方差分析*

杨　柳，王　钰1.山西财经大学 应用数学学院，太原 030006.山西大学 软件学院，太原 030006

组块3×2交叉验证的F1度量的方差分析*

杨柳1+，王钰2
1.山西财经大学 应用数学学院，太原 030006
2.山西大学 软件学院，太原 030006

YANG Liu,WANG Yu.Analysis of variance of F1 measure based on blocked 3×2 cross validation.Journal of Frontiers of Computer Science and Technology,2016,10(8)：1176-1183.

摘要：在统计机器学习的研究中，研究者常常通过定量实验来对照基于交叉验证的分类算法的F1度量，为了得到统计可信的结论，估计它的不确定性是非常重要的。特别地，组块3×2交叉验证方法被大量理论和实验验证了它的性能优于诸如标准K折交叉验证的其他常用交叉验证方法。为此，理论上研究了基于组块3×2交叉验证的F1度量的方差。方差的结构表明它由块方差、块内协方差和块间协方差三部分组成，从而说明了广泛使用的样本方差估计可能严重地低估或高估真实的方差。通过条形图方法在模拟和真实数据上进行实验，验证了上述理论结果，实验结果表明块内、块间协方差和块方差是同阶的，块内和块间相关性是不可忽略的。

关键词：F1度量；交叉验证；方差；分类算法；模拟实验

1　引言

在诸如自然语言处理的统计机器学习应用中，F1度量是分类算法性能度量的最常用指标之一。在一篇典型的统计学习文章中，新提出的算法相对于以前已经存在的算法F1值上有些许的提高，就被作者声称他们的方法优于其他方法，但这些许的提高极有可能是由随机误差导致的。因此，为了得到统计可信的结论，需要借助于统计显著性检验（置信区间）来判定它显著与否。为了减小随机性的影响，基于各种交叉验证的统计检验方法被提出，其中最广泛使用的基于标准K折交叉验证和RLT交叉验证的t检验方法已经在许多文献中被研究[1-5]。文献[6]指出传统的标准K折交叉验证由于训练集中训练样本重叠，常常导致其方差被低估，进而影响检验性能，为此，他们提出了基于2折交叉验证5次重复的5×2交叉验证t检验方法。在此基础上，文献[7-8]提出了用于两个分类算法性能对照的更稳健的联合5×2交叉验证F检验和t检验。然而，无论是5×2交叉验证F检验还是t检验，都是直接基于2折交叉验证的5次独立重复实验进行的，但实际上无论怎样划分数据，得到的训练集之间都包含有相同的样本，即它们之间实际上是不独立的。这样，5×2交叉验证中的独立性假定将导致5×2交叉验证F检验和t检验中的样本方差（严重）低估它们的真实方差，从而导致得到的检验是激进的（liberal），即此检验由于过于自信可能容易导致错误的结论。特别地，文献[9]指出5×2交叉验证F检验和t检验由于其5次重复的训练和测试样本重叠个数不同而无法进行方差的理论分析，从而导致方差估计，以及进一步的假设检验比较困难，为此他们提出了具有相同重叠样本个数的组块3×2交叉验证的组块3×2交叉验证t检验。

然而，上述用于算法性能对照的统计检验方法都是基于损失函数的，本文考虑把组块3×2交叉验证应用于F1度量。因为在自然语言处理中，真实的语料库往往比较小，并且为了减小随机误差，基于交叉验证的方法常常被用于F1度量的推断。又文献[9-11]理论和实验验证了组块3×2交叉验证方法优于K折交叉验证和5×2交叉验证，为此考虑把组块3×2交叉验证方法应用于F1度量。为了得到可信的统计显著性检验或置信区间，必须对它的方差进行分析。这样，本文研究了基于组块3×2交叉验证的F1度量的方差。方差的结构表明，广泛使用的样本方差估计可能严重地低估或高估真实的方差，并通过模拟实验进行了验证。

2　性能的度量

在统计学习的研究中，有多个度量分类算法性能的指标，包括泛化误差、错误率、精确率、准确率（precision）、召回率（recall）、F得分、ROC（receiver operating characteristics）曲线，AUC（area under the ROC curve）等[1,12-14]。本文关注于基于准确率和召回率调和平均的F1值度量，它是F得分的一种特殊情形。

2.1标准的F1度量

不失一般性，本文仅考虑简单的两类分类问题，每个系统都包含两个类别标签，用于标示样本的正例和负例。分类算法依据给定的输入给出一个预测，通过对照预测和系统的真实类别标签，可以给出如下的一个2×2混淆矩阵。

表1中，TP（true positives）表示真实正例样本被正确分类为正例样本的数目；TN（true negatives）表示真实负例样本被正确分类为负例样本的数目；FP （false positives）表示真实负例样本被错误分类为正例样本的数目；FN（false negatives）表示真实正例样本被错误分类为负例样本的数目。基于得到的TP、TN、FP和FN，可以计算准确率p和召回率r：

为了综合评价准确率和召回率，文献中提出了如下的F1度量，它定义为准确率和召回率的调和平均：

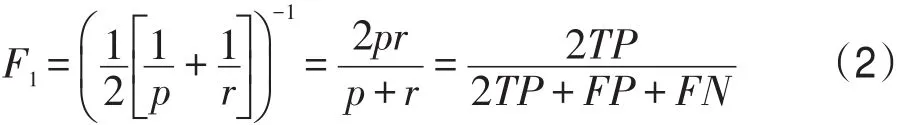
Table 1　Confusion matrix表1混淆矩阵

2.2基于组块3×2交叉验证的F1度量

为了检验算法之间性能差异的显著性，文献[6-8]提出了一个基于损失函数的随机5×2交叉验证方法，并通过模拟实验验证了它的性能优于常用的10折交叉验证方法。

具体地，数据集D={z1,z2,…,zn},zi=(xi,yi)∈Z是从分布P中独立抽样得到的，xi是输入向量，yi是输出变量。首先，数据集D被分成容量（大致）相等的不相交的两部分，重复这样的划分5次，得到的训练和测试集分别被记为,i=1,2,…,5,k=1,2。这样，基于随机5×2交叉验证的F1度量可以写为：

k,i=1,2,…,5, k=1,2,是互为训练和测试集的，因此,i=1,2,…,5。然而，文献[9]指出随机5×2交叉验证的方差的精确理论表达式不能得到，从而导致其方差估计，以及进一步的假设检验比较困难。并且他们指出任意两个2折交叉验证之间的协方差和训练集之间的重叠样本个数有关，在n/4时达到最小，见图1。

Fig.1　Covariance curve as the change of the number of overlapped sample图1　随着重叠样本个数变化的协方差曲线

接着，他们提出了具有相同重叠样本个数（均为n/4）的泛化误差的组块3×2交叉验证估计，本文把它应用于F1度量。这样，基于组块3×2交叉验证的F1度量被定义为3组2折交叉验证的F1得分的平均：

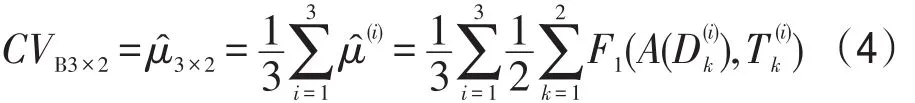
3　组块3×2交叉验证的F1度量的方差结构

鉴于组块3×2交叉验证是3组2折交叉验证的平均结果，那么由方差和的方差公式知，组块3×2交叉验证的方差具有如下形式：

引理1[3,9]基于组块3×2交叉验证的F1度量的协方差矩阵具有如下简单形式：

引理2[2,9]令U1,U2,…,UK为均值E(Uk)=β，方差Var(Uk)=Δ，协方差Cov(Uk,Uk′)=γ,k≠k′,k,k′=1,2,…, K的随机变量，π=γ/Δ为Uk和Uk′的相关系数，分别为样本均值和样本方差，那么

（2）如果对所有的K上述协方差结构都成立，即γ和Δ不依赖于K，则γ≠0；

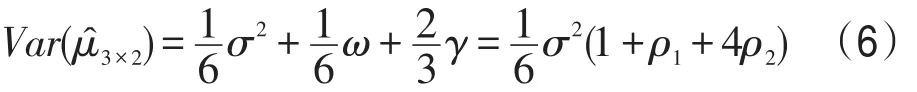
i≠i′,k=k′或者k≠k′,i,i′=1,2,3,k,k′=1,2。

证明 由引理1和引理2知：

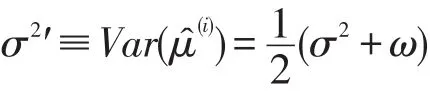
对任意i≠i′，有：

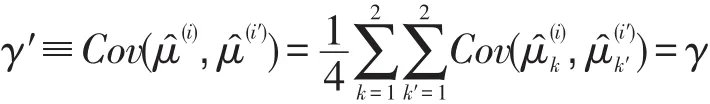
因此，基于引理2：

4　模拟实验

实验1模拟数据的两类分类实验。

考虑两类分类问题：X=(X1,X2,…,Xp)为p维输入向量（特征向量），Y={0,1}表示二元响应变量，实验目的为通过这p个特征变量来构造分类器对类别0和1进行分类。特别地，假定两类取值的概率相同，即P(Y=1)=P(Y=0)=1/2，在响应变量Y条件下特征变量X服从正态分布，即X|Y=0～N(0,I30),X|Y=1～N (1,2I30),N(Normal)表示正态分布，I30表示30×30的单位矩阵。分别用如下4个分类器进行分类，考察在样本量分别为n=40,80,160,200,400,800,1 200, 1 600,2 000时组块3×2交叉验证的F1度量的方差以及它的三部分分量的变化。

（1）分类树（classification trees，CT）分类器：把输入（特征）空间划分为一系列的区域，形成一个树状结构，在每个区域拟合一个简单模型，然后基于某个准则（如误分类误差）进行分类。

（2）最近邻（nearest neighbour，NN）分类器：寻找训练集在输入空间中最邻近待考查样本的K个样本点，通过这K个点的投票实现分类。

（3）朴素贝叶斯（naïve Bayes，NB）分类器：假定特征空间中各特征之间是独立的，由各特征的类条件边缘密度的乘积近似各类条件密度，然后使用贝叶斯定理进行分类。

（4）支持向量机（suport vector machine，SVM）分类器：通过基展开（核函数）对原始特征进行变换来扩大特征空间，然后在扩大的特征空间上构造最优分类超平面实现分类。

由图2～图5可以看到，组内协方差ω有相对较小的影响，但组间协方差γ对方差的贡献是和σ2同阶的，甚至更大。实际上，随着样本容量的变化，σ2对总方差的解释仅占到30%～40%。这个实验也验证了在F1度量上有与损失函数度量相同的结论：当考虑组块3×2交叉验证的F1度量的方差时，组间的相关性不能被忽略。为了进一步验证这个结论，给出了在真实letter数据集上多个分类器和多个样本量下组内和组间相关性ρ1和ρ2的变化。

实验2真实letter数据集上的分类实验。

letter数据集包含20 000个样本，16个特征变量，响应变量Y是26个罗马字母，实验的目的就是通过这16个特征变量来对26个罗马字母进行分类[15]。为了简化这个分类问题，类似于文献[2]，把它转化为一个二类分类问题：A～M为一类，N～Z为另一类。与模拟数据类似，在样本量 n=40,80,160,200,400, 800,1 200,1 600,2 000时，采用分类树（CT）、最近邻（NN）、朴素贝叶斯（NB）、支持向量机（SVM）分类器进行ρ1和ρ2真值的模拟。

Fig.2　Bar chart with different sample sizes for CT classifier图2　CT分类器各样本量下的条形图

Fig.3　Bar chart with different sample sizes for NN classifier图3　NN分类器各样本量下的条形图

Fig.4　Bar chart with different sample sizes for NB classifier图4　NB分类器各样本量下的条形图

Fig.5　Bar chart with different sample sizes for SVM classifier图5SVM分类器各样本量下的条形图

由表2和表3可以看到，对所有的分类器，随着样本量的增加，组内相关性ρ1逐渐减小，组间相关性ρ2趋于某一个稳定值，这和文献[9]基于损失函数得出的结论是一致的。例如，在分类树分类器下，随着样本量增加到2 000，ρ1已经趋于一个接近于0的值0.007。在除了SVM的其他3个分类器下，ρ2都稳定在一个小于0.4的范围内，对于SVM分类器，在样本量为800和1 600时，ρ2超过了0.4但也小于0.5。这些都进一步说明了在考虑组块3×2交叉验证的方差时，ρ1和 ρ2不能被忽略，尤其是组间的相关性。特别注意的是，在NB分类器下产生了负的组内相关性，像引理2指出的那样，它可能是因为协方差和K的选取有关导致的，但在此没办法进行进一步的分析，因为这里的K是固定的，等于3。其中λ1=1-

Table 2　True values ofρ1andρ2with CT and NN classifiers表2　CT和NN分类器下ρ1和ρ2的真值

文献中，常常通过样本方差来进行方差的估计。但是，在此如果使用假定组内和组间相关性全为0时的样本方差

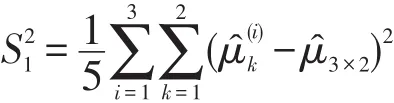
和文献[6-8]中假定组间相关性为0时的样本方差来估计Var(μ̂3×2)的话，将导致比较大的偏差。

Table 3　True values ofρ1andρ2with NB and SVM classifiers表3　NB和SVM分类器下ρ1和ρ2的真值

由表4和表5可以看到，在所有样本量和分类器下，λ1都是λ2的1.5倍到3倍。这表明样本方差估计有较大的偏差，但它是方差的一个保守估计。相对于λ1，λ3虽然有和λ2一样较小的偏差，但在一些情形下，将导致的激进估计，从而导致获得错误的结论。但无论是样本方差估计还是作为的估计，都有比较大的偏差，因此为了进行下一步的统计推断需要构造更合适的方差估计。

5　结束语

本文分析了基于组块3×2交叉验证的F1度量的方差，结果表明它可以简化随机3×2交叉验证的方差为一个只包含三项协方差的组合形式。模拟实验验证了这个简化的方差形式不能被进一步地简化，即组内和组间协方差和方差是同阶的，它们不能被忽略。

Table 4　Values ofλ1,λ2andλ3with CT and NN classifiers表4　CT和NN分类器下λ1、λ2和λ3的值

Table 5　Values ofλ1,λ2andλ3with NB and SVM classifiers表5　NB和SVM分类器下λ1、λ2和λ3的值

接下来，将研究组块3×2交叉验证的F1度量的方差估计问题，以及进一步的假设检验和区间估计问题。

References:

[1]Hastie T,Tibshrani R,Friedman J.The elements of statistical learning:data mining,inference,and prediction[M]. Berlin:Springer,2001.

[2]Nadeau C,Bengio Y.Inference for the generalization error[J]. Machine Learning,2003,52(3):239-281.

[3]Bengio Y,Grandvalet Y.No unbiased estimator of variance of K-fold cross validation[J].Journal of Machine Learning Research,2004,5:1089-1105.

[4]Grandvalet Y,Bengio Y.Hypothesis testing for cross validation,Tech Rep 1285[R].Montreal,Canada:University of Montreal,2006.

[5]Markatou M,Tian H,Biswas S,et al.Analysis of variance of cross-validation estimators of the generalization error[J]. Journal of Machine Learning Research,2005,6(7):1127-1168.

[6]Diettetich T.Approximate statistical tests for comparing supervised classification learning algorithms[J].Neural Computation,1998,10(7):1895-1924.

[7]Alpaydin E.Combined 5×2 cv F test for comparing supervised classification learning algorithms[J].Neural Computation,1999,11(8):1885-1892.

[8]Yildiz O.Omnivariate rule induction using a novel pairwise statistical test[J].IEEE Transactions on Knowledge and Data Engineering,2013,25(9):2105-2118.

[9]Wang Yu,Wang Ruibo,Jia Huichen,et al.Blocked 3×2 cross-validated t-test for comparing supervised classification learning algorithms[J].Neural Computation,2014,26 (1):208-235.

[10]Wang Yu,Li Jihong,Li Yanfang.Measure for data partitioning in m×2 cross-validation[J].Pattern Recognition Letters, 2015,65(11):211-217.

[11]Wang Yu,Li Jihong,Li Yanfang,et al.Confidence interval for F1 measure of algorithm performance based on blocked3×2 cross-validation[J].IEEE Transactions on Knowledge and Data Engineering,2015,27(3):651-659.

[12]Fawcett T.An introduction to ROC analysis[J].Pattern Recognition Letters,2006,27(8):861-874.

[13]Lobo J,Jimenez V,Real R.AUC:a misleading measure of the performance of predictive distribution models[J].Global Ecology and Biogeography,2008,17(2):145-151.

[14]Goutte C,Gaussier E.A probabilistic interpretation of precision,recall and F-score,with implication for evaluation[C]// LNCS 3408:Proceedings of the 27th European Conference on IR Research,Santiago de Compostela,Spain,Mar 21-23,2005.Berlin,Heidelberg:Springer,2005:345-359.

[15]Frey P W,Slate D J.Letter recognition using holland-style adaptive classifiers[J].Machine Learning,1991,6(2):161-182.

YANG Liu was born in 1979.She received the M.S.degree in mathematical statistics from Shanxi University in 2006.Now she is a lecturer at Shanxi University of Finance&Economics.Her research interests include statistical machine learning,probability and statistics,etc.

杨柳（1979—），女，山西临汾人，2006年于山西大学概率论与数理统计专业获得硕士学位，现为山西财经大学应用数学学院讲师，主要研究领域为统计机器学习，概率统计等。在国内外多种学术期刊上发表论文10多篇。

WANG Yu was born in 1981.He received the M.S.degree in mathematical statistics from Shanxi University in 2006.Now he is a lecturer at Shanxi University.His research interests include statistical machine learning and data mining,etc.

王钰（1981—），男，山西阳泉人，2006年于山西大学概率论与数理统计专业获得硕士学位，现为山西大学软件学院讲师，主要研究领域为统计机器学习，数据挖掘等。在国内外多种学术期刊上发表论文20多篇，现主持国家自然科学基金项目一项，参与国家和省级基金项目多项。

*The National Natural Science Foundation of China under Grant Nos.61503228,71503151(国家自然科学基金). Received 2016-03,Accepted 2016-06.

CNKI网络优先出版:2016-06-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160608.0931.002.html

文献标志码：A

中图分类号：TP181

doi:10.3778/j.issn.1673-9418.1603082

Analysis of Variance of F1 Measure Based on Blocked 3×2 Cross Validationƽ

YANG Liu1+,WANG Yu2
1.School ofApplied Mathematics,Shanxi University of Finance&Economics,Taiyuan 030006,China
2.School of Software,Shanxi University,Taiyuan 030006,China
+Corresponding author:E-mail:yang_liu@sxu.edu.cn

Abstract:In the research on statistical machine learning,researchers often perform quantitative experiments to compare F1 measure of classification algorithms based on cross validation.In order to obtain statistically convincing conclusion,it is very important to estimate the uncertainty of F1 measure.In particular,the blocked 3×2 cross validation is demonstrated that its performance is superior to other cross validation methods such as the standard K-fold cross validation by theory and experiments.Thus,this paper studies theoretically the variance of F1 measure based on blocked 3×2 cross validation.The structure of variance shows that it is composed of three parts:block variance,within-block covariance and between-blocks covariance,which also implies that the commonly used sample variance may grossly underestimate or overestimate the real variance.The above theoretical results are validated by the experiments in simulated and real data sets through bar chart method.The experimental results show that the within-block covariance and between-blocks covariance are of same order as the block variance.The within-block and between-blocks correlations can not be neglected.

Key words:F1 measure;cross validation;variance;classification algorithm;simulated experiment