结合各向异性中值扩散的PET图像重建算法*

何　骞，黄立宏1.湖南城市学院 信息科学与工程学院，湖南 益阳 41300.湖南大学 数学与计量经济学院，长沙 41008

结合各向异性中值扩散的PET图像重建算法*

何骞1,2+，黄立宏2
1.湖南城市学院 信息科学与工程学院，湖南 益阳 413002
2.湖南大学 数学与计量经济学院，长沙 410082

HE Qian,HUANG Lihong.PET image reconstruction algorithm combined with anisotropic median-diffusion. Journal of Frontiers of Computer Science and Technology,2016,10(8)：1166-1175.

摘要：为了有效提高正电子发射断层成像图像的质量，通过把各向异性中值扩散滤波器融合到中值根先验算法中，提出了一种新的基于Bayesian理论的图像重建算法。新算法的每次迭代过程都可以分为两步：首先用各向异性中值扩散滤波器抑制重建图像中的噪声；然后用中值根先验算法重建图像。仿真实验结果表明，在正电子发射断层成像中，新算法不仅能有效地抑制噪声，还能精确地保护图像的边缘。此外，与其他类似算法相比，新算法吸收了各向异性中值扩散滤波器的优点，在迭代过程中对梯度阈值和扩散次数不敏感，易于实现，实用性强。

关键词：正电子发射断层成像（PET）；各向异性中值扩散；中值根先验；图像重建；抑制噪声

1　引言

正电子发射断层成像（positron emission tomography，PET）是核医学领域比较先进的临床检查影像技术，是目前唯一可在活体上显示生物分子代谢、受体及神经介质活动的新型影像技术，现已广泛地应用于多种疾病的诊断以及新药物的开发等领域。但是由于放射性药物的低剂量和欠采样等原因，采集到的投影数据经常会被噪声严重污染，即使最好的图像重建算法也不能抑制重建图像中的所有噪声，并且精确地保护图像的边缘等有用信息，因此寻找一种能够有效提高重建图像质量的算法是十分必要的。

在经典的PET图像重建算法中，最大似然-期望最大（maximum-likelihood expectation-maximization，MLEM）算法[1]是一种广泛使用的算法，它的工作原理很简单，就是寻找一个图像使得测量数据最有可能发生。和著名的滤波反投影（filtered back-projection，FBP）算法相比，MLEM算法由于考虑了测量数据的统计特性，其重建图像的质量明显优于FBP算法。但是MLEM算法是一个“病态算法”（不适定算法），因为它的解有可能不存在、不唯一或者不稳定[2]。现在，解决这个问题的有效方法一般是通过加入一个正则化项，把不适定的问题转化为适定的问题，从而达到提高重建图像质量的目的。这种方法被称为Bayesian算法[3]。Bayesian算法由于具有良好的降噪能力以及解唯一等优点，近年来得到了广泛的关注[3-8]。其中，最具代表性的算法是由Green提出的迟一步（one-steplate，OSL）算法[3]，此算法的关键是寻找一个合适的能量函数，它直接决定了算法性能的好坏。不幸的是，能量函数的选择十分困难。在文献[4]中，Alenius等人用一个中值滤波器来近似代替OSL算法中的能量函数，提出了著名的中值根先验（median root prior，MRP）算法，此算法虽在一定程度上提高了图像的质量，但是它没有与之相对应的目标函数，只是通过一种经验的方式推导出来，因此不是一种真正意义上的Bayesian算法。2003年，Hsiao等人在MRP算法的基础上，通过引入一个辅助向量，提出了中值先验（median prior,MP）算法[5]，它是一种真正意义上的Bayesian算法。

近年来，为了进一步提高重建图像的质量，基于偏微分方程的图像重建算法成为新的研究热点[9-15]。2007年，颜建华和于军把各向异性扩散（anisotropic diffusion，AD）滤波器引入到MP算法中，提出了偏微分方程-中值（partial differential equation median，PDE-median）算法[10]。后来，桂志国等人对PDEmedian算法做了进一步的改进，如用非局部模糊各向异性扩散滤波器代替PDEmedian算法中的AD滤波器等[9]。这些算法都在一定程度上提高了重建图像的质量，但是由于滤波器的缺陷，这些算法对梯度阈值和扩散次数都十分敏感，实际运用中很难实现。

为了解决以上算法中参数设置困难的问题，本文把各向异性中值扩散滤波器（anisotropic mediandiffusion，AMD）[16]和MRP算法结合起来，提出了一种新的基于Bayesian的PET图像重建算法，称为各向异性中值扩散-中值根先验算法（anisotropic mediandiffusion median root prior，AMDMRP）。新算法能在有效抑制重建图像中噪声的同时精确地保护图像的边缘，并且对梯度阈值和扩散次数不敏感，易于实现，实用性较强。

2　算法基础

2.1中值根先验算法

1996年，Alenius等人根据PET图像的特点，提出了著名的MRP算法。此算法用一个中值滤波器来近似代替OSL算法中能量函数的导数，是OSL算法的一个应用推广。MRP算法可用以下公式来表示[4]：

其中，f(∙)表示重建图像；i表示像素编号；k表示迭代次数；表示重建图像中，编号为i的像素的邻域内的中值（邻域的大小一般是一个3×3的矩形空间）；β是Bayesian参数，主要用来设置先验信息的权重。

MRP算法的每次迭代过程都需要计算MLEM和Bayesian两个系数，MLEM系数主要负责重建图像，而Bayesian系数主要负责抑制重建图像中的噪声，并且保护图像的边缘等细小结构[4]。如果重建图像中含有噪声（局部不单调），则的值不相等，那么Bayesian系数的值就不等于0，于是Bayesian系数就能抑制重建图像的噪声。相反，如果重建图像中不含噪声（局部光滑），那么由于的值相等，Bayesian系数的值等于0，从而MRP算法就退化为MLEM算法。MRP算法虽然能在较好地抑制噪声的同时保护重建图像的边缘，但是随着迭代过程的进行，重建图像中容易产生伪影（“分块”现象），这些伪影将严重影响临床诊断的结果。此外，由于MRP算法没有与之相对应的目标函数，只是通过一种经验的方式推导出来，因而它不是一种真正意义上的Bayesian算法。为了解决这个问题，2003年，Hsiao等人在MRP算法的基础上，通过引入一个辅助向量，提出了一种新的Bayesian算法——中值先验算法（MP）[5]。在PET图像重建的过程中，MRP算法的每个像素值接近于它的局部中值，而MP算法的每个像素值接近于它的局部中值的中值，因此这两种算法的重建效果十分相似[5]。

2.2各向异性中值扩散滤波器

AD滤波器（又称为P-M模型）是一种非线性、自适应的滤波器，目前已经广泛地使用于医学图像重建等领域，它的基本方程是[17]：

其中，t是一个时间参数；f(x,y,0)表示原始的发射图像；div是散度算子；∇f(∙)是梯度算子；g(∙)是扩散系数函数。Perona和Malik提出了以下两个经典的扩散系数函数：

其中，k表示梯度阈值，用来判断此区域是否是一个局部边缘。

AD滤波器的基本思想就是根据图像内容的不同而采取不同的平滑方式，即平滑强度（抑制噪声的能力）在边缘区域减弱，而在非边缘区域增强，从而达到抑制噪声并且保护图像边缘的目的。因此，P-M模型中梯度阈值的选择很重要，它直接决定了AD滤波器性能的好坏。但是在一个被噪声严重污染的PET图像中，选取一个合适的梯度阈值是十分困难的。为了有效地解决这个问题，Ling和Bovid提出了各向异性中值扩散滤波器[16]。AMD模型把中值滤波器引入到P-M模型中，每次滤噪的过程都分为两步：首先通过式（2）滤除图像中具有小梯度值的噪声；然后再用一个中值滤波器滤除图像中具有大梯度值的噪声。它的扩散系数函数是：

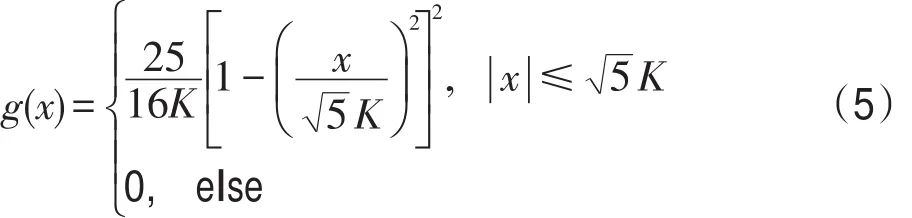
此外，AMD模型中扩散过程只是滤除具有小梯度值的噪声，而对那些具有大梯度值的噪声，是通过中值滤波器来抑制的，因此AMD滤波器对梯度阈值和扩散次数不敏感。当扩散次数不是很小，且梯度阈值不比梯度的标准偏差大很多时，滤噪效果都很接近[16]。

3　基于AMD模型的Bayesian图像重建算法

2007年，颜建华和于军提出的PDEmedian算法在一定程度上提高了重建图像的质量，是一种真正意义上的Bayesian图像重建算法。在介绍新算法之前，首先简单地介绍一下PDEmedian算法的框架。PDEmedian算法是通过最小化以下两个能量函数得到的[10]：

其中，Ψ(∙)是一个非负非减函数；l(f)是对数似然函数；ΦP(f;m)是先验函数。由于邻域内绝对值势函数的最优化解等于邻域经过中值滤波的结果，为了和MRP算法相关联，ΦP(f;m)函数定义如下：

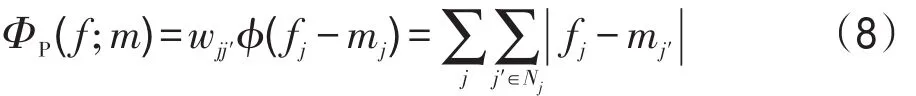
其中，Nj表示像素 j的邻域。当 j′∈Nj时，wjj′=1，否则，wjj′=0。

接下来，简单分析PDEmedian算法的收敛性。Hsiao等人[5]证明了，如果势函数ϕ是凸的，则先验函数ΦP(f;m)也是凸的。在式（8）中，ϕ是绝对值势函数，它是凸的，并且由于l(f)也是凸的，能量函数E2必是一个凸函数。因此，E1和E2的联合估计必定是收敛的，所求的解必定是一个全局最小解。

PDEmedian算法中梯度阈值K和扩散次数l很重要，它们共同决定了算法性能的好坏。如果K和l的值太小，则不能有效地滤除重建图像中的噪声，扩散过程效果不明显。相反，如果K和l的值太大，则会使得重建图像的边缘模糊，从而丢失大量重要的信息。但是在一个低信噪比的PET图像中，噪声产生的梯度可能超过边缘产生的梯度，此时要选择一组合适的参数是十分困难的。因此，对PDEmedian算法还需要做进一步的研究。

本文在PDEmedian算法的基础上，通过把AMD模型融合到MRP算法中（由于MP算法与MRP算法的重建结果十分相似，为了实验的方便，跟PDEMedian算法一样，用MRP算法近似代替MP算法），提出了一种新的Bayesian图像重建算法——AMDMRP算法。新算法的每次迭代更新过程都可以分为两步：首先运用AMD模型抑制重建图像中具有小梯度值的噪声；然后用MRP算法重建图像，并且进一步抑制具有大梯度值的噪声。具体迭代公式如下：

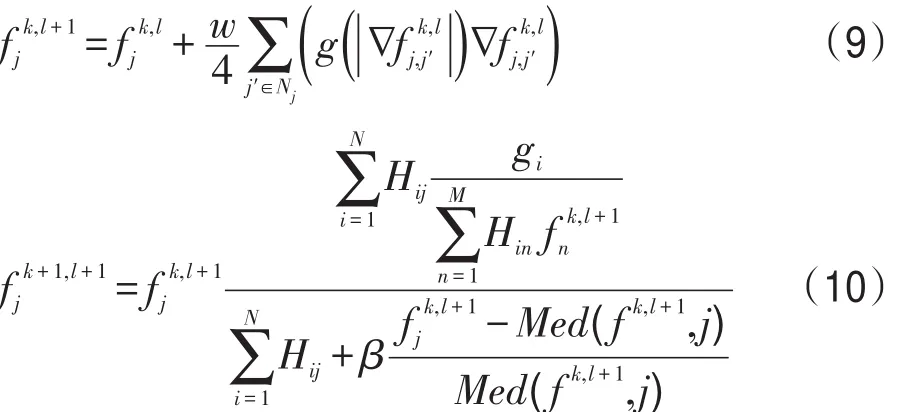
其中，k表示迭代次数；j表示像素编号；f表示重建图像；Hij是系数矩阵，表示像素 j发出的光子，被第i对探测器对捕获的概率；gi表示第i对探测器对捕获的光子总数；w是用来表示扩散率的一个常量；∇fj,j′=fj′-fj；Nj表示 j号像素的邻域；Med(∙)和β的定义如前所述；扩散系数函数g(∙)的定义如式（5）所示。

考虑到AMD模型对扩散次数不敏感，为了简化AMDMRP算法的参数设置，规定扩散次数和迭代次数相等，都等于k，那么AMDMRP算法的迭代公式可简单地表示为：

AMDMRP算法的具体运行步骤如下：

步骤1通过扩散过程（式（11））抑制噪声。

步骤2通过MRP算法重建图像（式（12））。

步骤3判断是否满足迭代终止条件，如果满足，则转步骤4，否则，转步骤1。

步骤4结束。

在AMDMRP算法的每次迭代过程中，扩散过程（式（11））用来滤除具有小梯度值的噪声，而具有大梯度值的噪声却被接下来MRP算法（式（12））中的中值滤波器滤除，但是对那些同样具有大梯度值的边缘来说，MRP算法却不会影响它们。因此，在AMDMRP算法中，AMD滤波器和MRP算法能够相互协同合作，在滤除重建图像中噪声的同时精确地保护图像的边缘。

4　仿真实验结果及分析

为了验证AMDMRP算法在PET中的有效性，对AMDMRP算法和PDEmedian、MRP以及MLEM算法进行比较。在模拟仿真实验中，首先采用的测试图像是由计算机产生的，大小为128×128像素的Shepp-Logan头部模型，图像中每个像素点的灰度取值范围都在0～255之间，如图1所示。假设投影参数的大小为128×128，即有128个投影方向（均匀分布在0～π之间），并且每个投影方向上有128对探测器。利用公式g=Hf产生无噪声的观测数据，用该投影数据作为泊松变量的均值生成实际带噪声的投影数据。在仿真实验中，采集到的光子总量约为6×105对。

Fig.1　Shepp-Logan phantom图1　Shepp-Logan模型

为了公平，在仿真实验中所有算法的迭代次数都设定为50次，Bayesian参数β在AMDMRP、PDE-median和MRP算法中都设置为0.3（这3种算法对β都不敏感）。在PDEmedian算法中，根据经验（能取得较好的重建结果）把梯度阈值K和扩散次数l都设定为40。在AMDMRP算法中，通过参考图像的梯度直方图，把梯度阈值K设定为10（AMDMRP算法对梯度阈值不敏感，见图7）。

4种算法对头部模型的重建图像如图2所示，图3是图2的局部扩大图像。由这些图可以看出，MLEM算法的重建效果最差，它的重建图像中含有大量的噪声；PDEmedian算法的重建效果虽然优于MRP和MLEM算法，但是重建图像中边缘比较模糊，丢失了大量的细节信息。相比之下，AMDMRP算法不仅有效地抑制了重建图像中的噪声，还良好地保护了重建图像的边缘，取得了较好的视觉效果。

Fig.2　Shepp-Logan phantoms reconstructedby 4 different algorithms图2　4种算法对Shepp-Logan模型的重建图像

Fig.3　Zoomed images of Fig.2图3　图2的局部扩大图像

为了从客观上评价AMDMRP算法的有效性，使用了NRMSE和SNR两个定量评价指标：

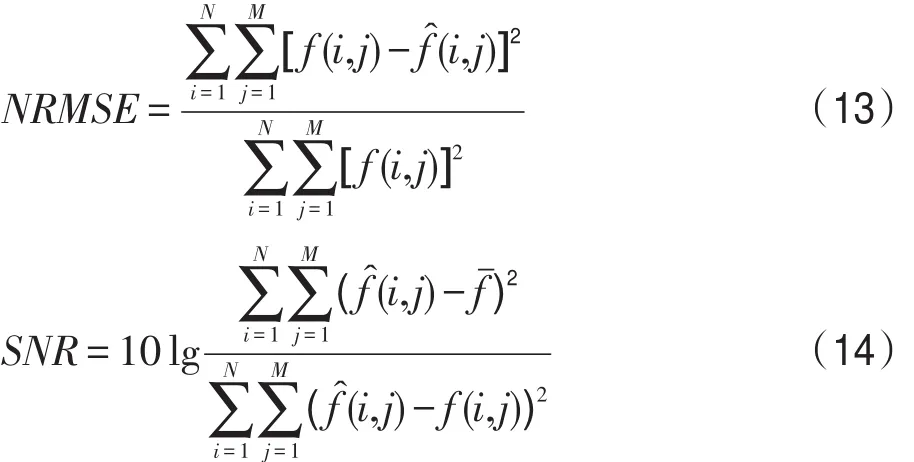
图4是4种算法重建图像的NRMSE值随迭代次数变化的曲线图。由图4可知，新算法的NRMSE值是最小的，说明它的重建图像与原始图像最接近，重建效果最好。类似的结论也可以通过分析图5的SNR变化曲线图得到。

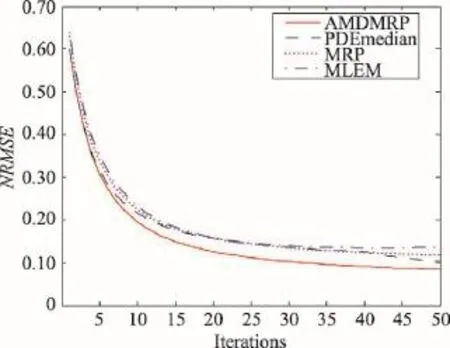
Fig.4　Plots of NRMSE along with iterations for Shepp-Logan phantoms reconstructed by 4 algorithms图4　4种算法对Shepp-Logan模型重建图像的NRMSE值随迭代次数变化的曲线图

接下来，通过与PDEMedian算法的比较来说明AMDMRP算法的稳定性（对梯度阈值和扩散次数不敏感）。在以下实验中，规定Bayesian参数的值β= 0.3。图6是PDEmedian算法在不同的梯度阈值K和扩散次数l下对头部模型的重建图像，其中迭代次数k=50。由图6可知，PDEmedian算法对梯度阈值和扩散次数十分敏感，它们共同决定了算法重建效果的好坏。当K和l的值都比较小时，算法不能有效地抑制重建图像中的噪声，如图6（a）所示；相反，当K 和l的值都比较大时，虽然能够抑制重建图像中的噪声，但是会使得图像的边缘模糊，从而丢失大量的细节信息，如图6（c）和（d）所示。因此，在PDEmedian算法中选择一组合适的参数，使得重建算法既能有效滤噪，又能良好地保护图像的边缘是十分困难的。只有通过多次反复的实验，才能选取一组合适的参数。在本实验中，图6（b）取得了相对较好的重建效果。图6中4个图的NRMSE和SNR值如表1所示。图7是AMDMRP算法在不同的梯度阈值K和扩散次数k下对头部模型的重建图像。由图可知，AMDMRP算法对梯度阈值不敏感（只要K值不比梯度的标准偏差大很多）。图7中4个图像都很接近，都取得了较好的重建效果。它们的NRMSE和SNR值如表2所示。

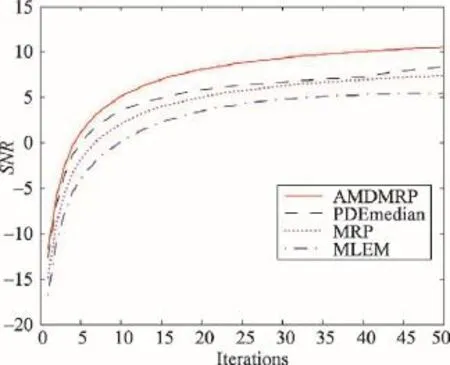
Fig.5　Plots of SNR along with iterations for Shepp-Logan phantoms reconstructed by 4 algorithms图5　4种算法对Shepp-Logan模型重建图像的SNR值随迭代次数变化的曲线图

为了进一步说明算法的有效性，采用胸腔模型为测试模型。胸腔模型的大小为128×128像素，如图8所示。投影数据的获取方式和前面的方法类似，采集到的光子总数约为5.4×105对。

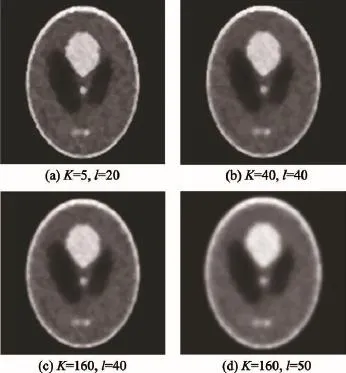
Fig.6　Shepp-Logan phantoms reconstructed by PDEmedian algorithm with different gradient thresholdsKand diffusion numbersl图6　PDEmedian算法在不同的梯度阈值K和扩散次数l下对Shepp-Logan模型的重建图像

Table 1　NRMSE and SNR values for 4 reconstructed images in Fig.6表1图6中4个重建图像的NRMSE和SNR值

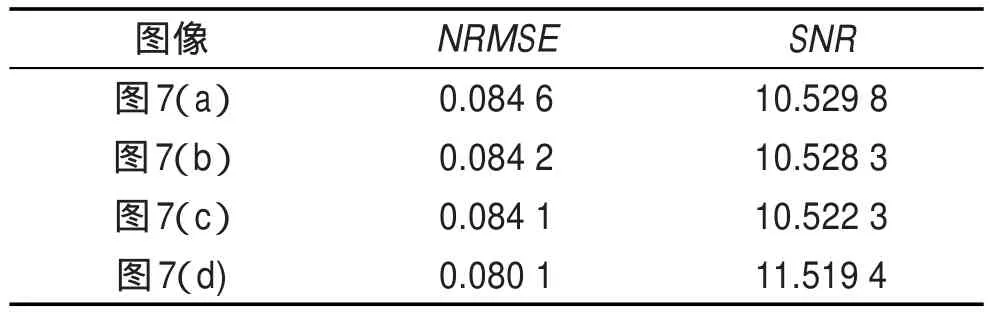
Table 2　NRMSE and SNR values for 4 reconstructed images in Fig.7表2图7中4个重建图像的NRMSE和SNR值

Fig.7　Shepp-Logan phantoms reconstructedAMDMRP algorithm with different gradient thresholds Kand diffusion numbersk图7AMDMRP算法在不同的梯度阈值K和扩散次数k下对Shepp-Logan模型的重建图像

同样，对AMDMRP算法和PDEmedian、MRP和 MLEM算法进行比较。规定所有算法的迭代次数都是50，Bayesian参数β在AMDMRP、PDEmedian和MRP算法中都设置为0.3。在PDEmedian算法中，根据经验把梯度阈值K和扩散次数l分别设定为20和40。在AMDMRP算法中，通过参考图像的梯度直方图，把梯度阈值K设定为20。

Fig.8　Thorax phantom图8胸腔模型

图9是以上4种算法对胸腔模型的重建图像，它们的局部扩大图像如图10所示。由这些图可以看出，AMDMRP算法的重建图像效果最好，它在滤噪和边缘保护两方面取得了较好的折中。图11和图12分别是以上4种算法的NRMSE和SNR值随迭代次数变化的曲线图，它们也客观地说明了AMDMRP算法的有效性。

Fig.9　Thorax phantoms reconstructed by 4 different algorithms图9　4种算法对胸腔模型的重建图像

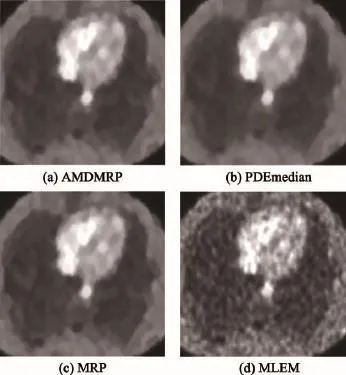
Fig.10　Zoomed images of Fig.9图10　图9的局部扩大图像

图13是AMDMRP算法在不同梯度阈值和扩散次数下对胸腔模型的重建图像。其中，Bayesian参数的值都是β=0.3。图中4个重建图像十分相似，说明了AMDMRP算法对梯度阈值和扩散次数不敏感。图13中4个重建图像的NRMSE和SNR值如表3所示。

Fig.11　Plots of NRMSE along with iterations for thorax phantoms reconstructed by 4 algorithms图114种算法对胸腔模型重建图像的NRMSE值随迭代次数变化的曲线图

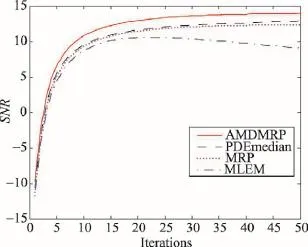
Fig.12　Plots of SNR along with iterations for thorax phantoms reconstructed by 4 algorithms图12　4种算法对胸腔模型重建图像的SNR值随迭代次数变化的曲线图

5　结束语

为了有效提高PET重建图像的质量，本文通过把各向异性中值扩散滤波器和MRP算法结合起来，提出了一种新的Bayesian图像重建算法——AMDMRP算法。模拟仿真实验结果表明，无论是从主观的视觉效果还是客观的质量评价参数来看，新算法的性能都要好于PDEmedian、MRP和MLEM算法。新算法在抑制噪声和保护边缘两方面取得了良好的折中，较大程度地提高了重建图像的质量。此外，和PDEmedian算法相比，新算法吸收了各向异性中值扩散滤波器的优点，在迭代过程中对梯度阈值和扩散次数不敏感，易于实现，实用性较强。但是还存在一些问题，需要予以关注，主要总结如下：

Fig.13　Thorax phantoms reconstructed byAMDMRP algorithm with different gradient thresholds Kand diffusion numbersk图13AMDMRP算法在不同的梯度阈值K和扩散次数k下对胸腔模型的重建图像

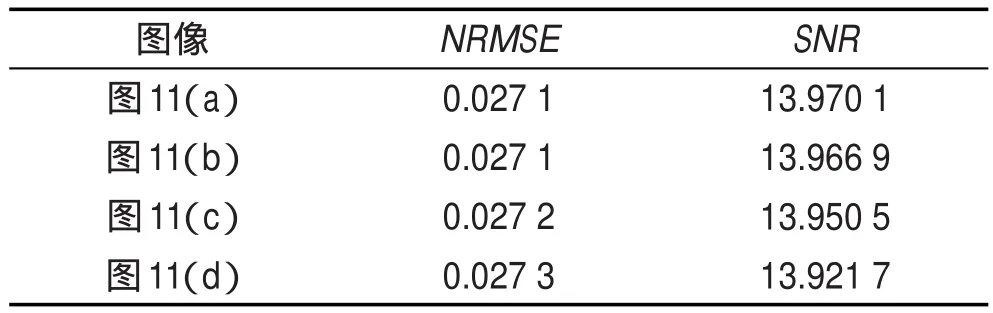
Table 3　NRMSE and SNR values for 4 reconstructed images in Fig.13表3图13中4个重建图像的NRMSE和SNR值

（1）算法的收敛速度是判断一个算法性能好坏的重要指标。本文算法没有考虑收敛速度的问题，下一步可以考虑在收敛速度方面对它做进一步的优化，如可以考虑把有序子集的概念用于此算法等。

（2）统计迭代算法中迭代终止条件的设置是一个至今尚未解决的难题，本文是通过设置固定迭代次数来实现终止迭代的。下一步思考如何寻找一个更合适的迭代终止条件来避免“过分迭代”的问题。

（3）本文算法主要用于二维图像重建，下一步将考虑三维图像重建的问题。所谓三维图像重建是指利用二维投影恢复物体三维信息（形状等）的数学过程和计算机技术，包括数据获取、预处理、特征分析和立体匹配等步骤。其中立体匹配是三维图像重建的核心，它要根据所提取的特征来建立图像对之间的一种对应关系，也就是将同一物理空间点在两幅不同图像中的成像点一一对应起来。在进行匹配时要注意场景中一些因素的干扰，比如光照条件、噪声干扰、物体几何形状畸变、表面物理特性以及摄像机机特性等诸多变化因素。此外，三维图像重建的计算量比二维图像重建大很多，因此如何提高重建算法的运算速度也是三维图像重建中一个重要的研究课题。

References:

[1]Shepp LA,Vardl Y.Maximum likelihood reconstruction for emission tomography[J].IEEE Transactions on Medical Imaging,1982,1(2):113-122.

[2]Gaitanis A,Kontaxakis G,Spyrou G,et al.PET image reconstruction:a stopping rule for the MLEM algorithm based on properties of the updating coefficients[J].Computerized Medical Imaging and Graphics,2010,34(2):131-141.

[3]Green P J.Bayesian reconstructions from emission tomography data using a modified EM algorithm[J].IEEE Transactions on Medical Imaging,1990,9(1):84-93.

[4]Alenius S,Ruotsalainen U.Bayesian image reconstruction for emission tomography based on median root prior[J]. European Journal of Nuclear Medicine,1997,24(3):258-265.

[5]Hsiao I T,Rangarajan A,Gindi G.A new convex edgepreserving median prior with applications to tomography[J]. IEEE Transactions on Medical Imaging,2003,22(5):580-585.

[6]Guo Yu,Feng Yuanming,Sun Jian,et al.Automatic lung tumor segmentation on PET/CT images using fuzzy Markov random field model[J].Computational&Mathematical Methods in Medicine,2014(1):171-188.

[7]Norberg J,Roininen L,Vierinen J,et al.Ionospheric tomography in Bayesian framework with Gaussian Markov random field priors[J].Radio Science,2015,50(2):138-152.

[8]Jia Kun,Liang Shunlin,Wei Xiangqin,et al.Automatic land-cover update approach integrating iterative training sample selection and a Markov random field model[J].Remote Sensing Letters,2014,5(2):148-156.

[9]Gui Zhiguo,Liu Yi,He Jiawei.PML algorithm for positron emission tomography combined with nonlocal fuzzy anisotropic diffusion filtering[J].IEEE Transactions on Nuclear Science,2012,59(5):1984-1989.

[10]Yan Jianhua,Yu Jun.Median-prior tomography reconstruction combined with nonlinear anisotropic diffusion filtering[J]. Journal of the Optical Society of America A,2007,24(4): 1026-1033.

[11]He Qian,Huang Lihong.Penalized maximum likelihood algorithm for positron emission tomography by using anisotropic median-diffusion[J].Mathematical Problems in Engineering,2014(1):1-7.

[12]Meng Xianyong,Che Lei,Liu Zhihui,et al.Towards a partial differential equation remote sensing image method based on adaptive degradation diffusion parameter[J].Multimedia Tools&Applications,2015:1-17.doi:10.1007/ s11042-015-2881-1.

[13]Wang Liping,Zhou Shangbo,KarimA.Super-resolution image reconstruction method using homotopy regularization[J]. Multimedia Tools&Applications,2015:1-24.doi:10.1007/ s11042-015-2910-0.

[14]Wang L,Sixou B,Peyrin F.Binary tomography reconstructions with stochastic level-set methods[J].IEEE Signal Processing Letters,2015,22(7):920-924.

[15]Fathi A,Kallivokas L F,Poursartip B.Full-waveform inversion in three-dimensional PML-truncated elastic media[J]. Computer Methods in Applied Mechanics&Engineering, 2015,296:39-72.

[16]Ling J,Bovik A C.Smoothing low-SNR molecular images via anisotropic median-diffusion[J].IEEE Transactions on Medical Imaging,2002,21(4):377-384.

[17]Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

HE Qian was born in 1983.He received the M.S.degree from College of Information Engineering,Xiangtan University in 2009.Now he is a Ph.D.candidate at Hunan University,and lecturer at Hunan City University.His research interests include image processing and medical image reconstruction,etc.

何骞（1983—），男，湖南益阳人，2009年于湘潭大学信息工程学院获得硕士学位，现为湖南大学数学与计量经济学院博士研究生，湖南城市学院讲师，主要研究领域为图像处理，医学图像重建等。

HUANG Lihong was born in 1963.He received the Ph.D.degree from Department of Applied Mathematics,Hunan University in 1996.Now he is a professor and Ph.D.supervisor at Hunan University.His research interests include neural network,differential equation and dynamical system,etc.

黄立宏（1963—），男，湖南湘阴人，1996年于湖南大学应用数学系获得博士学位，现为长沙理工大学党委委员、副校长，湖南大学教授、博士生导师，湖南省数学学会副理事长，主要研究领域为神经网络，微分方程，动力系统等。发表学术论文200余篇，主持承担973前期研究专项课题1项，国家自然科学基金项目6项，其他国家与省部级科研和教研项目30余项。

*The National Natural Science Foundation of China under Grant No.11371127(国家自然科学基金);the Scientific Research Foundation of Hunan Provincial Education Department under Grant No.15C0253(湖南省教育厅科研项目).

Received 2016-02,Accepted 2016-05.

CNKI网络优先出版:2016-05-13,http://www.cnki.net/kcms/detail/11.5602.TP.20160513.1434.002.html

文献标志码：A

中图分类号：TP391

doi:10.3778/j.issn.1673-9418.1602044

PET Image ReconstructionAlgorithm Combined withAnisotropic Median-Diffusionƽ

HE Qian1,2+,HUANG Lihong2
1.College of Information Science and Engineering,Hunan City University,Yiyang,Hunan 413002,China
2.College of Mathematics and Econometrics,Hunan University,Changsha 410082,China
+Corresponding author:E-mail:heqian0808@163.com

Abstract:For improving the quality of positron emission tomography(PET)images,this paper proposes a new Bayesian image reconstruction algorithm by combining anisotropic median-diffusion filter with median root prior algorithm.Iterations of the proposed method can be divided into two steps:firstly,suppressing noise with the anisotropic median-diffusion filter;secondly,reconstructing image with median root prior algorithm.Simulation experiment results present that the proposed algorithm can effectively suppress noise and accurately preserve edges information in PET image reconstruction.Furthermore,in comparison to other similar reconstruction algorithms,the proposed method absorbs the advantages of the anisotropic median-diffusion filter and is less sensitive to the selection of the image gradient threshold and diffusion number,thus making the application of PET image reconstruction feasible.

Key words:positron emission tomography(PET);anisotropic median-diffusion;median root prior;image reconstruction;suppressing noise