基于EEMD和ARIMA模型的汽轮机故障趋势预测
剡昌锋,易 程,吴黎晓,韦尧兵
(兰州理工大学 机电工程学院,甘肃 兰州 730050)
基于EEMD和ARIMA模型的汽轮机故障趋势预测
剡昌锋,易程,吴黎晓,韦尧兵
(兰州理工大学 机电工程学院,甘肃 兰州 730050)
由于汽轮发电机转子振动状态监测数据具有非线性和非平稳性,采用普通时间序列预测模型时预测的精度较低。研究通过分析振动信号的频率成分,融合EEMD分解平稳化处理和ARIMA预测模型的思想,建立一种混合预测模型。结果表明:该方法能够适应振动状态监测数据特征,反映了振动状态的主要变化趋势,具有较高的预测精度以及更大的应用范围,其预测趋势对进一步进行振动状态分析具有一定的参考价值。
EEMD;ARIMA;趋势预测;频率成分
汽轮发电机组是电力生产的重要设备,通过状态监测实现实时故障诊断和设备预知性维修具有重要的实用价值[1,2]。转子振动状态监测数据反映了机械系统的主要变化规律,蕴含着丰富的故障征兆信息,对其实时监测有助于进行故障趋势预测[3]。同时,由于机械系统结构的复杂性和运行环境的特殊性,导致了状态监测数据具有海量性、高维性、动态性和复杂性等特点,采用单一的状态趋势预测方法很难满足在不同条件下取得较理想的预测效果。常用状态趋势预测方法有基于统计学的传统方法、人工智能方法、传统方法与人工智能结合的混合预测方法,其中时间序列自回归滑动平均(ARMA,auto-regressive and moving average)模型因其简单直观、运算方便且执行快速而被普遍使用。Box等[4]针对非平稳随机时间序列运用累计差分的方法提出了差分自回归滑动平均(ARIMA,auto-regressive integrated moving average)时间序列预测模型。Babu等[5]将线性预测模型和非线性预测模型相结合建立了ARIMA-ANN模型,同时运用移动平均滤波器处理数据,进行单步或多步预测时都具有较高的预测精度,但是该方法需要大量数据来进行模型参数的估计。
除了直接对状态监测数据进行预测外,通过进行数据预处理对预测效果也能起到很好的改善作用[6],例如基于经验模态分解的时间序列预测方法[7]、基于离散小波分解的时间序列预测方法[8]等。这些方法试图通过预处理过程,将状态监测数据进行降噪以及平稳化处理,然后利用平稳时间序列模型对其加以预测,可以有效提高状态趋势预测的可靠性。
研究提出了一种基于集合经验模分解(EEMD,ensemble empirical mode decomposition)和ARIMA模型的振动状态趋势预测方法,通过对状态监测数据运用形态滤波器进行降噪预处理,从分析振动信号频率成分的角度出发,利用EEMD并计算互相关系数筛选出相关分量,对各分量建立ARIMA模型形成混合预测框架,预测非平稳时间序列的趋势变化。该方法能够适应状态监测的数据特征,提高了状态趋势预测质量,同时具有较强的应用价值。
1 混合趋势预测模型
旋转机械在运行过程中,系统参数的观测值之间具有显著的关联性,这种关联性是机械系统内部动力学行为的外在表现,也是状态趋势预测的基础。但是,这种关联性会随着状态参数频率的增大而使不同时刻的数据相关性减小,如果直接对快速变化参数进行趋势预测也就意义不大,则需要转换预测指标来进行有效地趋势预测。通过对连续缓变的状态监测数据建立时间序列模型可以揭示数据之间的这种显著关联性,依据时间序列模型对有限的历史数据进行延拓,从而实现对状态趋势的预测来获知复杂机械系统的运行状况。从试验现场采集到的振动信号包含多种形式的随机噪声,减弱了这种关联性,数据的预处理可以降低随机噪声而提高数据的可靠性和精确度。频率成分反映了振动信号的内在结构本质,运用自适应信号分解的方法并依据互相关系数筛选出最相关的分量和趋势分量,因为它们是影响振动状态趋势变化的决定性因素。研究提出基于EEMD和ARIMA模型相结合的混合趋势预测方法,对转子振动状态监测数据进行预测。通过编程实现的流程如图1所示。

图1 混合趋势预测框架Fig.1 Prediction frame of the mixed trend
具体步骤如下:(1)载入状态监测数据,对数据的噪声进行评价,采用组合形态滤波器滤除脉冲随机噪声,提高信噪比;(2)运用EEMD方法将时间趋势序列自适应分解成为一系列不同尺度的本征模态函数(IMF,intrinsic mode function)分量和残余分量,进行平稳化处理;(3)分别计算各分量的互相关系数筛选出有效IMF分量和趋势分量;(4)对筛选出的每个IMF分量和趋势分量进行ARIMA建模预测;(5)最后将预测结果相叠加,即可得到非平稳振动状态趋势序列的预测值。
2 混合预测方法的建立
2.1形态滤波器
数学形态学是1964年由法国Matheron G和Serra J在积分几何研究成果的基础上创立的,通过一定形态的结构元素定量地描述图像结构特征来识别和分析图像[9]。基于数学形态学理论的形态滤波器是通过一个结构元素对图像进行卷积运算,结构元素大小和形状的确定以及操作的选择决定输出的结果,作为一种重要的工具广泛应用于噪声抑制、图像分割等[10]。
为了避免由于开、闭运算时对数值的扩大或缩小,采用广义开-闭和闭-开运算的线性组合的形态滤波器进行降噪处理,无需考虑信号的频谱特征,算法简单且执行高效,能消除标准形态算子产生的偏差的同时较好地保持了数据的几何结构特征,有效滤除脉冲随机噪声,即可提高信噪比[11]。同时,结构元素在形态滤波器中的作用类似于一般信号处理时的滑动窗,其形状和大小对腐蚀、膨胀运算产生很大的影响。待处理数据的形状决定了结构元素的形状设计,其结构要尽可能接近待分析的图形特点。我们选择圆形结构元素,其宽度主要由状态监测数据主要波形的周期和采样频率决定。
2.2EEMD分解
为了分析信号的频率成分,Huang等[12]提出了一种将非线性、非平稳的时间序列分解为一系列不同尺度的IMF之和的自适应信号分解的方法,即经验模式分解方法EMD。如果时间序列数据中包含高频间歇振荡成分,EMD分解得到的IMF分量往往会存在模态混叠效应,从而影响了该方法自适应分解信号的性能。针对EMD存在的不足,Wu等[13]提出将噪声作为辅助信号处理的方法来解决模态混叠效应,即集合经验模式分解方法EEMD。EEMD的具体计算过程如下:
(1)参数设置:依据时间序列的标准偏差设置集成次数NE以及添加的白噪声的幅值a,集成次数从1开始。集成次数NE、白噪声的幅值a和标准差σ之间的关系可表示为[14]

(1)
通过大量模拟和试验后,提出了一个用来确定EEMD算法中参数的自适应准则[14]:白噪声幅值常取为标准差的0.1~0.4倍之间,当高频成分占主导地位时,添加白噪声的幅值应适当减小;当低频成分占主导地位时,添加白噪声的幅值应适当增大;一般集成次数设置为100。
(3)循环重复步骤(2),直到预先设定的集成的次数NE。
(4)计算分解得到的IMF分量的均值,并将其作为EEMD分解的最终结果。
但是,由于插值误差、边界效应等原因,EEMD在分解过程中会产生一些伪分量(即与原始信号无关的分量),这些伪分量没有任何物理含义并容易对信号频率成分分析造成干扰。通过计算各IMF分量与原始信号互相关系数的大小来判定IMF的真伪,计算公式为

(2)
其中:Rx,cj(τ)为各IMF分量与原始信号的互相关系数;Rx(τ)为自相关系数。
虽然EEMD分解后残余分量的互相关系数较小,但体现了状态趋势变化的长期走向,将其作为趋势项进行建模预测。这样对复杂非线性、非平稳信号通过EEMD分解成若干个简单有效的非线性、非平稳信号,使趋势序列数据进行平稳化处理,可以扩大时间序列模型的应用范围,更加有利于应用时间序列模型进行状态趋势预测。
2.3ARIMA模型的建立
(1)模型描述ARMA模型是以时间序列的自相关分析为基础,用数学模型来近似描述这个随机时间序列,通过系统辨识确定模型参数,然后根据时间序列的历史值和现在值来预测时间序列的未来值。ARMA模型可近似表示为
yt=φ1yt-1+φ2yt-2+…+φpyt-p+at-θ1at-1-θ2at-2-…-θqat-q,
(3)
其中:p为自回归阶数;φ1,φ2,…,φp为自回归系数;q为滑动平均阶数;θ1,θ2,…,θq为滑动平均系数;at是白噪声序列服从正态分布,即at~N(0,σ2),则称时间序列{yt}服从(p,q)阶自回归滑动平均模型,简记为ARMA(p,q)。
若{yt}为非平稳时间序列,可以经过d次差分后成为平稳时间序列,即
φ(B)dyt=θ(B)at,
(4)
则称式(4)为(p,d,q)阶的差分自回归滑动平均模型,记ARIMA(p,d,q),其中d为差分次数。
(2)平稳化处理与模型识别对时间序列历史趋势数据首先运用时间序列平稳性检验函数进行平稳性检验,如果数据为非平稳时间序列且存在一定的上升或下降趋势,则需要进行差分平稳化处理。
通过计算平稳化后的时间序列的自相关函数和偏自相关函数来进行模型识别,揭示所研究的时间序列的特性来建立一个合适的模型[15]。具体计算公式有:
自协方差为
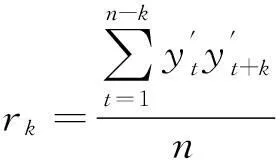
(5)
自相关函数为
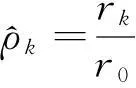
(6)
偏相关函数为
(7)

表1 ARMA(p,q)模型识别原则
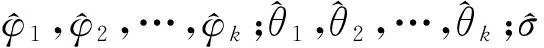
模型参数的最小二乘估计为
AIC=(n-d)logσ2+(p+q+1)logn,
(8)
其中:n为样本数;σ2为拟合残差平方和;d、p、q为模型参数。
(4)模型的检验与预测对所建立的模型要检验其是否能够满足平稳性和可逆性,即要求
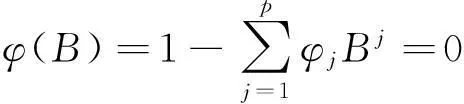
(9)
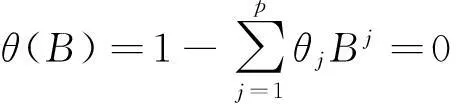
(10)
的根在单位圆外[15]。
进一步检验模型的残差序列是否为白噪声,如果不是,则需要重新建立模型;如果是,则通过检验,得出时间序列趋势预测模型。根据所建预测模型的外推预测性能进行预测,并考虑前面经过了d次差分运算,还原为原始趋势序列数据yt的预测结果,并计算预测结果与原始趋势序列的平均绝对误差及均方差来进行多角度的评价以及预测分析。
3 实验结果分析
为了验证基于EEMD和ARIMA混合预测模型的状态趋势预测效果,在汽轮发电机转子故障模拟试验台上进行振动状态监测的数据采集。选取转子出现故障时的状态监测数据来建立时间序列模型进行预测,以1~3 996共3 996个点作为历史状态样本数据,3 997~4 096共100个点作为预测对比数据来检验模型。采用平均绝对误差及均方差作为衡量模型预测精度的重要指标,计算公式有:
平均绝对误差为
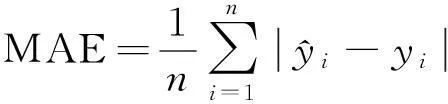
(11)
均方差为
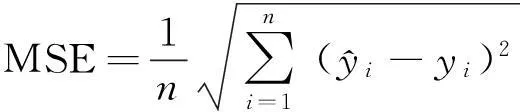
(12)
3.1状态监测数据预处理
载入状态监测数据后,运用组合形态滤波器滤除脉冲随机噪声进行数据的预处理,时间序列趋势如图2所示。
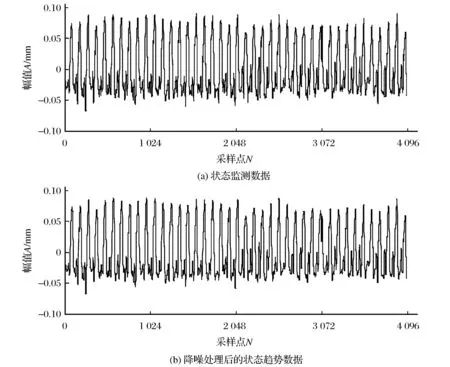
图2 时间序列趋势Fig.2 Chart of time series trend
3.2EEMD分解
对降噪后的趋势序列运用EEMD进行分解,共产生7个IMF分量和1个残余分量,EEMD分解结果如图3所示。各IMF分量与原始信号的互相关系数见表2。由表2可以看出,IMF4、IMF5和 IMF6这3个IMF分量的互相关系数较大,与原始信号呈显著的相关性,IMF8为趋势分量。筛选的这些相关分量反映了振动状态趋势变化的幅值和频率,相对于原始趋势序列变化较为平稳,更加有利于建立准确的时间序列模型,从而可以提高趋势变化的预测精度,也扩大了时间序列预测模型的应用范围。
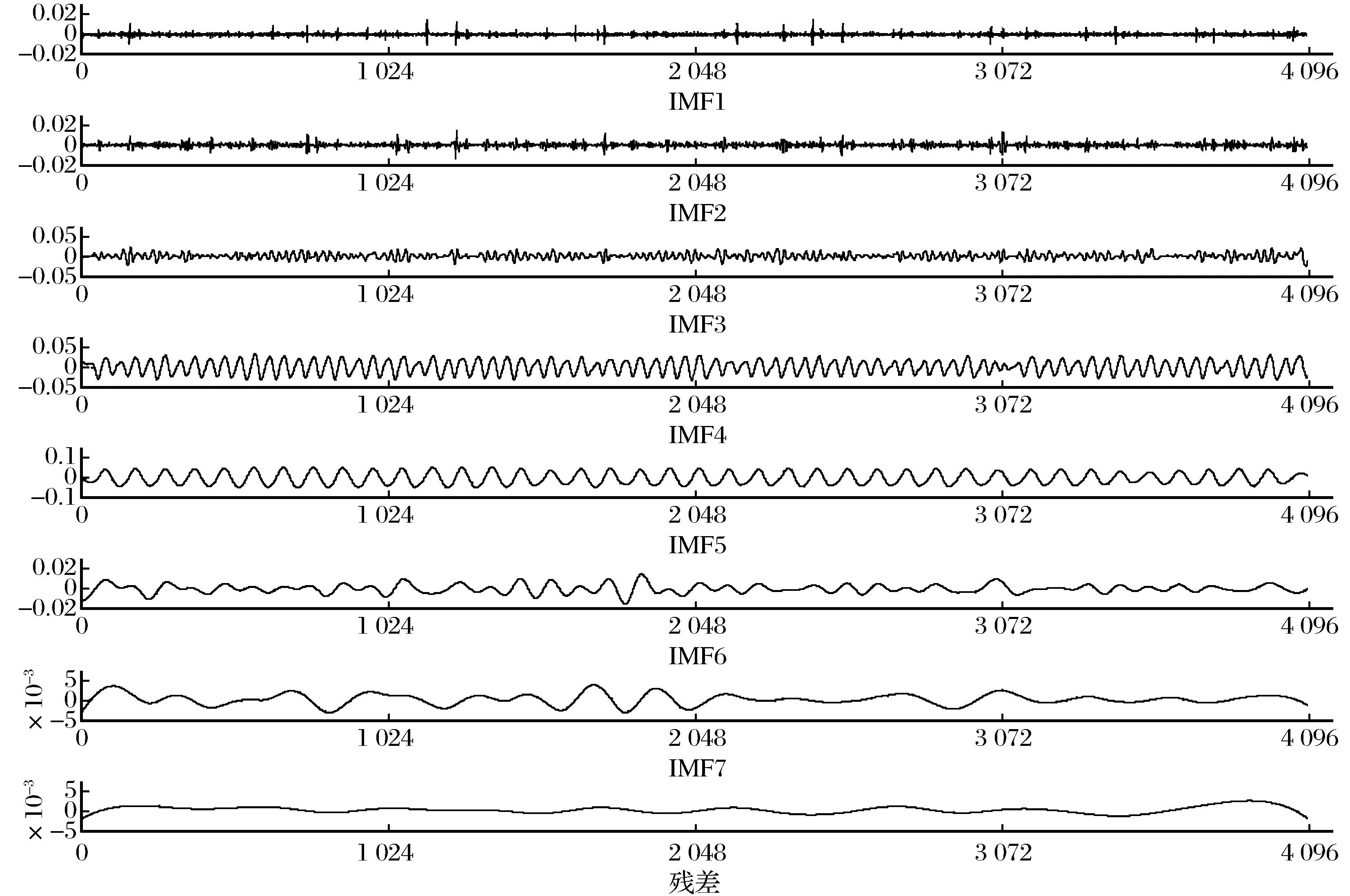
图3 EEMD分解结果Fig.3 EEMD decomposition results

IMFs12345678ρx,cj0.04440.11430.30900.59800.86130.53700.06380.0254
3.3建立ARIMA模型预测
对于筛选出来的各IMF分量和残余分量分别建立ARIMA模型进行状态趋势预测,确定出合适的模型参数,将所有分量的预测值叠加得到最终的状态趋势预测结果,如图4所示。为了进一步验证所提算法的可行性与有效性,采用 ARIMA 模型直接对该趋势序列进行了预测,模型预测与实际值的对比如图5所示。通过对比两种算法的预测结果的误差分析来评价预测模型的可靠性和算法性能,如表3所列。
由图5可以看出所建模型能够描述不对中故障状态的趋势变化规律且跟踪速度较好,能够快速响应状态监测数据的急剧变化,使得预测趋势曲线较好的反映了实测趋势变化。表3的误差分析指标对比结果也表现了混合ARIMA模型有着较小的平均绝对误差和均方差,趋势预测效果优于ARIMA模型。根据上述预测结果综合对比分析可以得出,通过对非平稳状态监测数据进行降噪预处理,运用EEMD依据信号内在频率结构特征将其分解为一系列平稳且具有一定规律的单一分量并通过互相关系数筛选出有效分量和趋势分量,建立混合预测模型,这样建立的趋势预测方法比直接应用时间序列预测模型降低了预测误差,更准确地反映出振动状态趋势变化,提高了状态趋势预测的准确性。但是EEMD分解得到的分量比较多,同时需要确定的参数相对较多,复杂度有一定程度的提升,这样就会在一定程度上影响混合预测模型的预测速度。

图4 混合ARIMA模型预测结果与实际趋势序列对比Fig.4 Comparison of mixed ARIMA model prediction results and actual tendency sequence
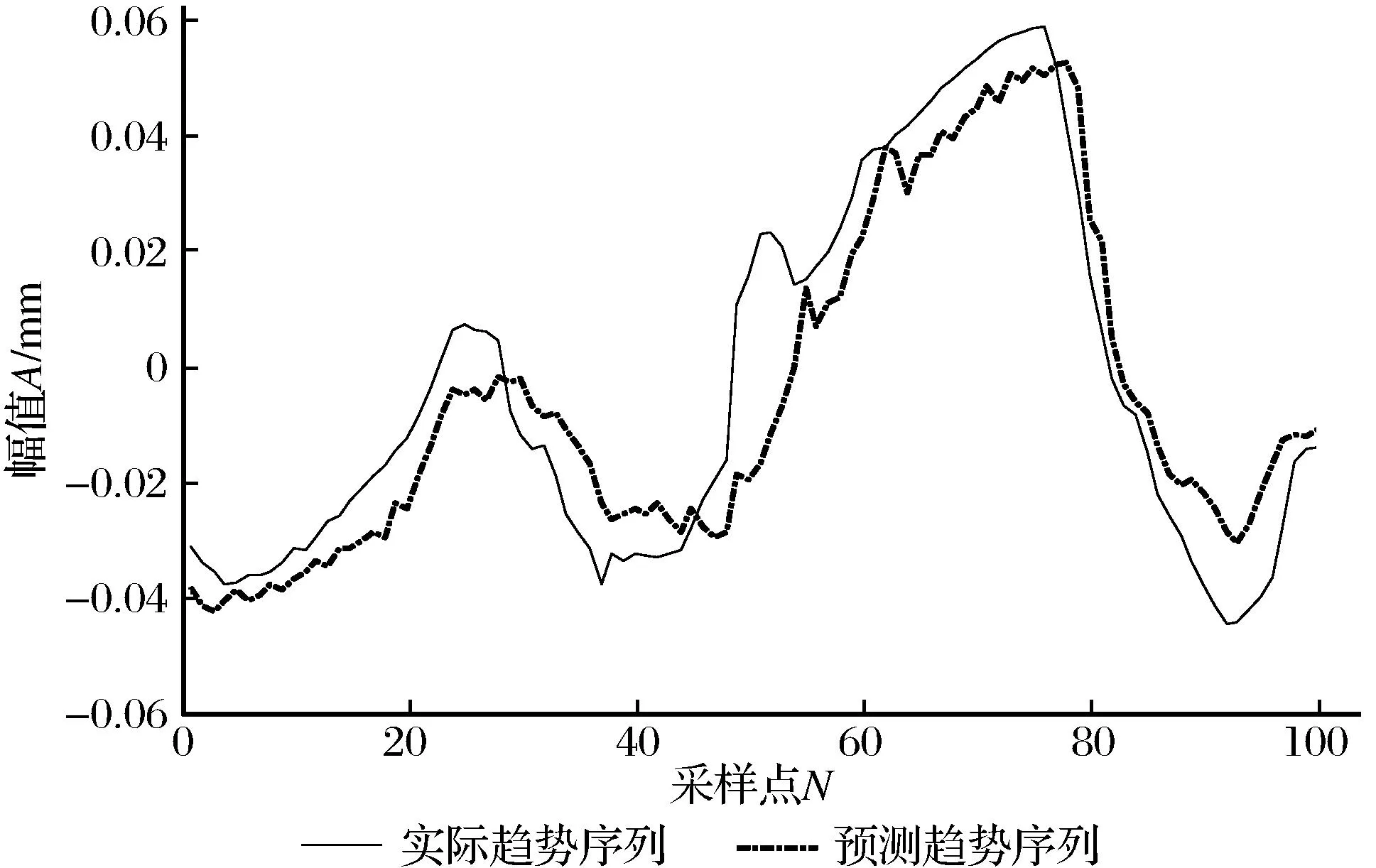
图5 ARIMA模型预测结果与实际值对比Fig.5 Comparison of ARIMA model prediction results and actual values

误差分析指标MAEMSE混合ARIMA模型0.00430.00049ARIMA模型0.01000.00120
4 结论
由于旋转机械振动状态监测数据具有海量性、非线性和非平稳性,直接建立时间序列预测模型会影响其预测精度。研究通过运用形态滤波器进行降噪预处理减小随机脉冲因素的干扰,运用EEMD分解并计算互相关系数筛选出有效分量和趋势分量,进行平稳化处理后建立ARIMA模型。试验结果表明该混合预测方法的有效性和适应性,能够预测出振动状态主要变化趋势且具有较高的预测精度以及更大的应用范围,其预测趋势对振动状态分析具有一定的参考价值。同时,由于状态监测数据变化的快慢程度以及模型参数适宜度的影响使少部分点的预测偏差较大,这就需要根据振动状态数据自身特点以及影响振动状态变化的物理因素,可以修正相关参数或者选择其他连续缓变的状态趋势预测指标以进一步提高故障趋势预测的准确性和可靠性。
[1]Laws W C,Muszynska A.Periodic and Continuous Vibration Monitoring for Predictive Maintenance of Rotating Machinery[J].Journal of Engineering for Gas Turbines and Power,1987,109(2):159-167.
[2]王红军,徐小力.支持向量机理论在设备状态趋势预测上的应用研究[J].兰州理工大学学报,2005,31(6):36-39.
[3]钟掘,陈安华.机械系统状态监测与故障诊断的重要课题[J].世界科技研究与发展,1996,18(6):15-19.
[4]Box G E P,Jenkins G M.Time Series Analysis:Forecasting and Control,Revised[M].San Francisco:Holden-Day,1976.
[5]Babu C N,Reddy B E.A Moving-average Filter Based Hybrid ARIMA-ANN Model for Forecasting Time Series Data[J].Applied Soft Computing,2014,23:27-38.
[6]刘莉,徐玉生,马志新.数据挖掘中数据预处理技术综述[J].甘肃科学学报,2003,15(1):117-119.
[7]祝志慧,孙云莲,季宇.基于 EMD 和 SVM 的短期负荷预测[J].高电压技术,2007,33(5):118-122.
[8]Huajun W,Lei S,Hongying L.Adjustments Based on Wavelet Transform ARIMA Model for Network Traffic Prediction[C]//Computer Engineering and Technology,2010 2nd International Conference on.IEEE,2010.
[9]Maragos P,Schafer R W.Morphological Filters--Part I:Their Set-theoretic Analysis and Relations to Linear Shift-invariant Filters[J].Acoustics,Speech and Signal Processing,IEEE Transactions on,1987,35(8):1 153-1 169.
[10]Serra J,Vincent L.An Overview of Morphological Filtering[J].Circuits,Systems and Signal Processing,1992,11(1):47-108.[11]张文斌,周晓军,林勇.广义形态滤波器在振动信号处理中的应用研究[J].农业工程学报,2008,24(6):203-205.
[12]Huang N E,Shen Z,Long S R,etal.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].Proceedings:Mathematical,Physical and Engineering Sciences,1998:903-995.
[13]Wu Z,Huang N E.Ensemble Empirical Mode Decomposition:A Noise-assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1):1-4.
[14]Guo W,Peter W T,Djordjevich A.Faulty Bearing Signal Recovery from Large Noise Using a Hybrid Method Based on Spectral Kurtosis and Ensemble Empirical Mode Decomposition[J].Measurement,2012,45(5):1 308-1 322.
[15]Shumway R H,Stoffer D S.Time Series Analysis and Its Applications:With R Examples[M].New York:Springer Science & Business Media,2010.
[16]Akaike H.Information Theory and an Extension of the Maximum Likelihood Principle[M].New York:Springer,1998.
Turbine Fault Trend Prediction that Based on EEMD and ARIMA Models
Yan Changfeng,Yi Cheng,Wu Lixiao,Wei Yaobing
(College of Mechno-Electronic Engineering,Lanzhou University of Technology,Lanzhou 730050,China)
Because of the nonlinearity and non-stationarity of the vibration condition monitoring data of the steam-turbine generator rotor,it has the low accuracy if it takes ordinary time series prediction model to make prediction.This papers analyzes the frequency components of the vibration signal,and integrate the thought of EEMD decomposition stationary processing and ARIMA prediction model to establish a mixed prediction model.Experimental results show that this method can adapt to the data characteristics of vibration condition monitoring,which has reflected the main trends of vibration state.It has higher accuracy and greater range of applications,and its forecast trends has a certain reference value for further analysis of the vibration state.
EEMD;ARIMA;Trend prediction;Frequency components
10.16468/j.cnki.issn1004-0366.2016.04.020.
2015-05-08;
2015-05-28.
国家自然科学基金项目(51165018).
剡昌锋(1974-),男,甘肃平凉人,研究员,博士研究生导师,研究方向为旋转机械状态监测及故障诊断.E-mail:changf_yan@163.com.
TH133
A
1004-0366(2016)04-0100-07
引用格式:Yan Changfeng,Yi Cheng,Wu Lixiao,etal.Turbine Fault Trend Prediction that Based on EEMD and ARIMA Models[J].Journal of Gansu Sciences,2016,28(4):100-106.[剡昌锋,易程,吴黎晓,等.基于EEMD和ARIMA模型的汽轮机故障趋势预测[J].甘肃科学学报,2016,28(4):100-106.]

