应用正交分析法分析岩石电性影响因素敏感性

董怀民，孙建孟，闫伟超，崔利凯



应用正交分析法分析岩石电性影响因素敏感性

董怀民，孙建孟，闫伟超，崔利凯

（中国石油大学地球科学与技术学院，山东青岛266580）

在分析岩石电性影响因素的基础上，提出了将正交分析法用于判别岩石电性影响因素的敏感性，以正交矩阵设计来分析岩石电性影响因素的水平组合，用方差分析法和趋势分析法对岩石电性影响因素的敏感性进行量化评价，从而区分影响岩石电性的主要因素和次要因素。对选取的岩心样品进行岩石电性数值模拟，结果表明，岩石电性对不同影响因素的敏感性不同，敏感性分析结果符合岩石电性数值模拟结果。

岩石电性；敏感性分析；正交分析法；方差分析法；趋势分析法；影响因素

岩石电性资料在测井解释、储集层评价以及储量计算中具有重要作用。影响岩石导电特性的因素众多，如岩石粒径、孔隙直径、微孔隙含量、水膜厚度、润湿性、泥质含量、导电矿物含量和地层水矿化度等，岩石电阻率实验难以定量测试和表征上述因素，而基于数字岩心的岩石物理数值模拟是一种行之有效的方法［1］。为此，选取了东海盆地西湖凹陷中北部NB-X气田花港组储集层典型泥质砂岩岩心，构建了三维数字岩心，采用有限元方法计算数字岩心电阻率［2］，探究影响岩石电性的各个因素的敏感性。

1　正交分析法概述

岩石电性影响因素敏感性分析，就是定量分析影响岩石电性的各因素与岩石电阻率之间的相关性，即分析各个影响因素的变化对岩石电性的影响程度［3］。目前，广泛采用的单因素分析法存在着明显的局限性，只能大体算出各个影响因素对考察指标的影响大小，计算量大，数据准备工作十分复杂。正交分析法可弥补单因素分析法的不足，本文采用正交分析法研究岩石电性对各个影响因素的敏感性，进而区分影响岩石电性的主要因素和次要因素。

正交分析法实际上是一种统计方法，利用已有的正交表来安排多因素实验，再对实验结果进行统计分析的科学方法［4］。利用正交分析法可以判断各个影响因素对所考察指标影响的大小顺序以及各个影响因素与考察指标的相互关系。

正交分析法的操作步骤可概括为：①根据筛选的影响因素和相应的水平数量选择合适的正交表Ln（rm），在各个影响因素水平给定条件下，通过正交表可确定实验方案［5］；②根据确定的实验方案进行实验，得到实验结果；③采用方差分析法分析实验结果，用各个影响因素的变差平方和与误差平方和相比，作方差齐性检验，从而判断实验结果对各影响因素的敏感性。

用正交表设计实验方案，每个影响因素同水平实验次数为t，则有n=rt，实验结果R1，R2，…，Rn，彼此相互独立，且服从方差σ2的正态分布，即Ri～N（ui，σ）（i=1，2，…，n），对Ri进行方差分析，可归结为对假设H0:u1=u2=…=un作敏感性检验，假设H0是方差齐性检验的固定假设，在这里可视为岩石电性对各个影响因素的敏感性相同。

实验结果的总偏差平方和QT和影响因素j的偏差平方和Qj分别为

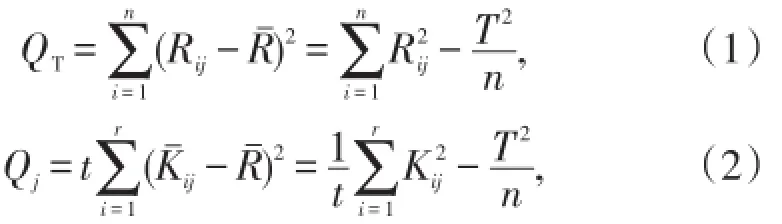
在正交分析中，有

总偏差平方和QT、单个影响因素j的偏差平方和Qj、误差平方和Qe的自由度分别为

构造的方差齐性检验统计量Fj为

对于给定的水平α，若Fj≥F1-α（fj，fe），则认为实验结果对影响因素j敏感；反之，则不敏感。若Fj≥F0.99（fj，fe），表明实验结果对影响因素j高度敏感；若F0.95（fj，fe）≤Fj＜F0.99（fj，fe），表明实验结果对影响因素j很敏感；若F0.90（fj，fe）≤Fj＜F0.95（fj，fe），表明实验结果对影响因素j较敏感；若Fj＜F0.90（fj，fe），表明实验结果对影响因素j不敏感。

2　岩石电性敏感性分析

选取了东海盆地西湖凹陷中北部NB-X气田花港组储集层典型渗透性泥质砂岩岩心，岩心样品实测孔隙度8.620%，泥质含量11.236%，导电矿物含量5.523%.对岩心样品进行X射线CT扫描［6］，扫描分辨率为1.331 μm，得到岩心样品的二维切片（图1a），采用滤波反投影技术处理，并将二维切片叠加，可构建出岩心样品的三维数字图像（图1b）［7-8］，数字岩心样品尺寸为400 pixel×400 pixel×400 pixel.经测算，构建的数字岩心样品孔隙度8.430%，泥质含量11.826%，导电矿物含量5.341%，与实测数值十分接近，可视为真实岩心。

图1　岩心样品数字图像

在选取岩石电性敏感性正交分析影响因素时，充分考虑到具体的可操作性和正交分析法的一般原理，参考前人对这一问题的研究成果［9-13］。经过筛选，选取了地层水矿化度、泥质含量、导电矿物含量、水膜厚度、岩石粒径和孔隙直径6个影响因素，进行岩石电性影响因素敏感性分析（表1）。

表1　不同影响因素水平下岩石电性影响因素敏感性分析

影响因素水平3是实测构建的数字岩心样品参数值，即地层水矿化度1 872.000 mg/L，泥质含量11.826%，导电矿物含量5.341%.影响因素水平2和水平1的参数值以影响因素实验方案3为基础，分别增加10%和20%，影响因素水平4和水平5分别减少10%和20%.

根据正交分析法的设计原则，选取的正交表为L25（56），为全面分析岩石电性对各个影响因素的敏感程度，设计了25个实验方案（表2）。根据设计的实验方案，即将表1中不同影响因素水平对应的参数值代入到表2中，采用有限元方法计算岩心样品在含水饱和度分别为41.10%和92.40%时的电阻率。

根据岩心样品在不同含水饱和度下电阻率，可计算不同含水饱和度下岩石电阻率影响因素的统计变量Kij，K¯ij及偏差平方和Qj.含水饱和度为41.10%和92.40%时岩石电阻率影响因素的统计变量Kij，K¯ij及偏差平方和Qj计算结果见表3和表4.

表2　正交分析法实验方案与结果

表3　岩心样品含水饱和度为41.10%时不同影响因素下统计变量计算结果

表4　岩心样品含水饱和度为92.40%时不同影响因素下统计变量计算结果

根据含水饱和度为41.10%和92.40%时岩石电阻率各统计变量计算结果，进行方差齐性检验，实验设计方案中影响因素j在所有水平下的偏差平方和Qj、平均偏差平方和、自由度fj和方差齐性检验统计量Fj可分别用（2）式、（4）式、（6）式和（8）式计算。选取水平α为0.01，0.05，0.10查方差齐性检验分布表可得：F0.99（4，4）=16.00，F0.95（4，4）=6.39，F0.90（4，4）=4.11.若Fj≥16.00，表示岩石电性对影响因素j高度敏感；若6.39≤Fj＜16.00，表示岩石电性对影响因素j很敏感；若4.11≤Fj＜6.39，表示岩石电性对影响因素j较敏感；若Fj＜4.11，表示岩石电性对影响因素j不敏感。

岩石电阻率各统计变量方差分析给出了影响岩石电性因素敏感性程度的定量分析结果，由表5方差分析结果可知：①在含水饱和度为41.10%时，岩石电性对地层水矿化度和导电矿物含量高度敏感，对泥质含量和孔隙直径很敏感，对水膜厚度和岩石粒径较敏感；②在含水饱和度为92.40%时，岩石电性对地层水矿化度、导电矿物含量和水膜厚度高度敏感，对泥质含量、岩石粒径和孔隙直径较敏感。

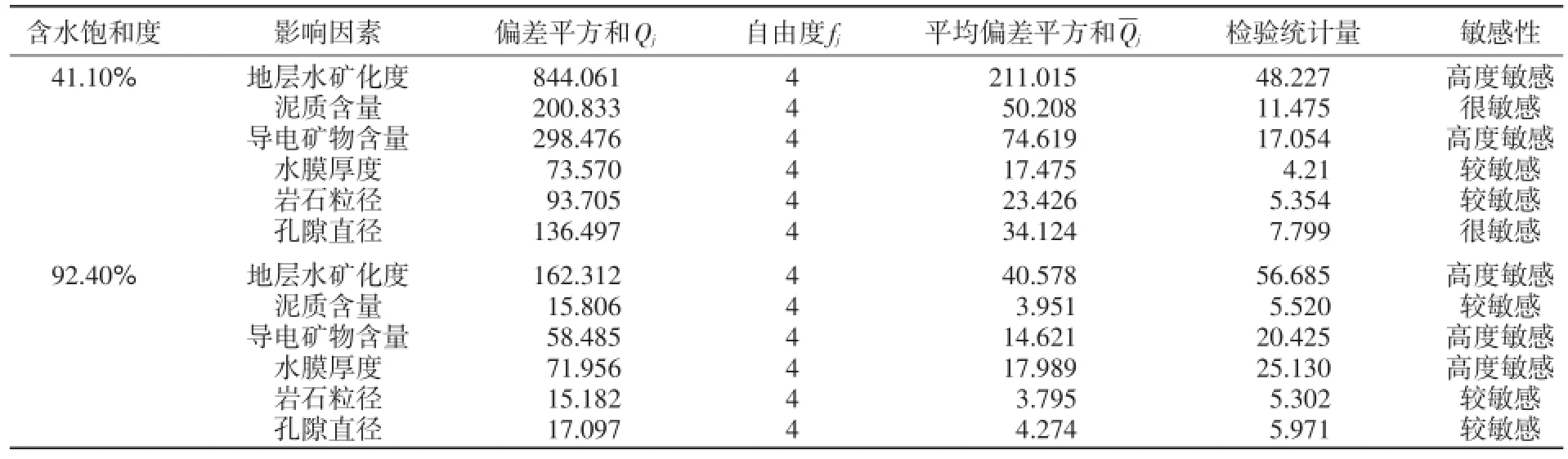
表5　不同含水饱和度时岩心样品方差分析结果

在含水饱和度分别为14.17%，26.20%，41.10%，60.70%，79.80%和92.40%时，岩石电性影响因素水平与在此水平下岩石电阻率统计变量平均值的变化趋势如下（图2）。①在含水饱和度不同，各影响因素以相同的水平差值增加时，电阻率统计变量平均值增幅各不相同。电阻率统计变量平均值增幅越大，表明岩石电性对此影响因素的敏感性越强；反之，则对此影响因素的敏感性越弱。②在低含水饱和度（Sw＜40%）时，泥质含量的电阻率统计变量平均值增幅最大，岩石粒径增幅最小，各影响因素电阻率统计变量平均值增幅由大到小依次为：泥质含量、地层水矿化度、导电矿物含量、水膜厚度、孔隙直径和岩石粒径。③在中等含水饱和度（40%≤Sw≤65%）时，地层水矿化度电阻率统计变量平均值增幅最大，孔隙直径增幅最小，各影响因素电阻率统计变量平均值增幅由大到小依次为：地层水矿化度、导电矿物含量、泥质含量、水膜厚度、岩石粒径和孔隙直径。④在高含水饱和度（Sw＞65%）时，地层水矿化度电阻率统计变量平均值增幅最大，水膜厚度增幅最小，各影响因素电阻率统计变量平均值增幅由大到小依次为：地层水矿化度、导电矿物含量、泥质含量、孔隙直径、岩石粒径和水膜厚度。

综上所述，岩石电性对6个影响因素的敏感性由强到弱依次为：地层水矿化度、导电矿物含量、泥质含量、孔隙直径、水膜厚度和岩石粒径。查阅相关文献［14-16］、实际模拟以及系统分析可知，对于不同的储集层、不同类别的岩石，各个影响因素的敏感性程度均不相同，并非一成不变。

图2　不同含水饱和度下影响因素水平与岩石电阻率统计变量平均值趋势示意

3　结论

影响岩石电性的因素有很多，并且各个影响因素对岩石电性的影响并非单纯的代数叠加之和，其相互作用十分复杂。对于不同的储集层、不同类别的岩石，各影响因素的敏感性程度均不相同，采用单因素分析法研究岩石电性影响因素的敏感性，工作量大、复杂，困难多、不易完成。

本文将正交分析法应用于影响岩石电性的各个影响因素的敏感性分析，不需要大量的岩石电性模拟样品，在一定程度上，极大地减少了电性模拟岩心样品数量，能有效地区分影响岩石电性的主要因素和次要因素。对于选取的储集层岩石样品而言，选择的6个影响岩石电性因素的敏感性排序由强到弱依次为：地层水矿化度、导电矿物含量、泥质含量、孔隙直径、水膜厚度和岩石粒径。

符号注释

fe——误差自由度，无量纲；

fj——影响因素j的自由度，无量纲；

fT——所有影响因素的自由度之和，无量纲；

Fj——构造的方差齐性检验统计量，无量纲；

Kij——影响因素j在i水平下的岩石电阻率统计变量，Ω·m；

L——正交表符号；

m——正交表列数，最多可设计的影响因素个数，个；

n——正交表行数，即设计的计算次数，次；

Qe——误差平方和，（Ω·m）2；

Qj——影响因素j的偏差平方和，（Ω·m）2；

Q¯j——影响因素j的平均偏差平方和，（Ω·m）2；

QT——所有影响因素的偏差平方和，（Ω·m）2；

r——水平个数，即设计的影响因素的状态个数，个；

Rij——影响因素j在i水平下所有实验结果之和，Ω·m；

Rij，k——影响因素j在i水平下第k个实验结果，Ω·m；

t——每个影响因素同水平的实验次数，次；

α——方差齐性检验中的参数，常数，无量纲。

［1］ARNS C H，BAUGET F，GHOUS A，et al.Digital core laboratory：petrophysical analysis from 3D images of reservoir core fragments［J］.Petrophysics，2005，46（4）：260-277.

［2］孔强夫，周灿灿，张艳，等.基于数字岩心岩石电性数值模拟方法综述［J］.地球物理学进展，2015，30（2）：718-724. KONG Qiangfu，ZHOU Cancan，ZHANG Yan，et al.Numerical simulation methods of rock electrical properties based on digital cores：a review［J］.Progress in Geophysics，2015，30（2）：718-724.

［3］蔡毅，邢岩，胡丹.敏感性分析综述［J］.北京师范大学学报（自然科学版），2008，44（1）：9-16. CAI Yi，XING Yan，HU Dan.On sensitivity analysis［J］.Journal of Beijing Normal University（Natural Science），2008，44（1）：9-16.

［4］梁飞豹，吕书龙，薛美玉，等.应用统计方法［M］.北京：北京大学出版社，2010. LIANG Feibao，LV Shulong，XUE Meiyu，et al.Methods of applied statistics［M］.Beijing：Peking University Press，2010.

［5］张艳红，杜修力.结构可靠度对系统参数敏感性分析的简便算法［J］.同济大学学报（自然科学版），1996，24（4）：475-480. ZHANG Yanhong，DU Xiuli.Simple sensitivity measures of reliability to system parameters［J］.Journal of Tongji University（Natural Science），1996，24（4）：475-480.

［6］ARNS C H.A comparison of pore size distributions derived by NMR and X-ray-CT techniques［J］.Physica A：Statistical Mechanics and its Applications，2004，339（1-2）：159-165.

［7］刘学锋.基于数字岩心的岩石声电特性微观数值模拟研究［D］.山东青岛：中国石油大学，2010. LIU Xuefeng.Numerical simulation of elastic and electrical properties of rock based on digital cores［D］.Qingdao，Shandong：China University of Petroleum，2010.

［8］姜黎明.基于数字岩心的天然气储层岩石声电特性数值模拟研究［D］.山东青岛：中国石油大学，2012. JIANG Liming.Numerical simulation of acoustic and electrical properties of natural gas reservoir rocks based on digital cores［D］.Qingdao，Shandong：China University of Petroleum，2012.

［9］吕洪志，李兴丽，顾保祥.渤海新近系低电阻率油层成因及测井响应特征［J］.中国海上油气，2006，18（2）：97-102. LÜ Hongzhi，LI Xingli，GU Baoxiang.Origins and log responses of neogene of low-resistivity oil pays in Bohai sea［J］.China Offshore Oil and Gas，2006，18（2）：97-102.

［10］冯进.基于数字岩石物理实验的岩石电性影响因素分析——以珠江口盆地（东部地区）中浅层砂岩储层为例［J］.中国海上油气，2012，24（6）：12-16. FENG Jin.An analysis of the factors to influence electrical properties of rocks baesd on a digital petrophysical experiment：a case of the middle-shallow sandstone reservoirs in Pearl river mouth basin（the eastern area）［J］.China Offshore Oil and Gas，2012，24（6）：12-16.

［11］邓杰，王震亮，高潮，等.定边张韩地区长2低渗储层敏感性分析［J］.西北大学学报（自然科学版），2011，41（2）：285-290. DENG Jie，WANG Zhenliang，GAO Chao，et al.Estimation of sensitivity of Chang 2 reservoir in Zhanghan area［J］.Journal of Northwest University（Natural Science Edition），2011，41（2）：285-290.

［12］邓杰，李彦婧，梁立平，等.鄂尔多斯盆地定边张韩地区长2储层敏感性特征［J］.石油地质与工程，2011，25（2）：64-66. DENG jie，LI Yanjing，LIANG Liping，et al.Chang 2 reservoir sensitive characteristics in Ordos basin Dingbian Zhanghan area［J］. Petroleum Geology and Engineering，2011，25（2）：64-66.

［13］孟召平，张纪星，刘贺，等.考虑应力敏感性的煤层气井产能模型及应用分析［J］.煤炭学报，2014，39（4）：593-599. MENG Zhaoping，ZHANG Jixing，LIU He，et al.Productivity model of CBM wells considering the stress sensitivity and its application analysis［J］.Journal of China Coal Society，2014，39（4）：593-599.

［14］郑菲，施小清，吴吉春，等.深部咸水层CO2地质封存数值模拟参数的全局敏感性分析——以苏北盆地盐城组为例［J］.吉林大学学报（地球科学版），2014，44（1）：310-318. ZHENG Fei，SHI Xiaoqing，WU Jichun，et al.Global parametric sensitivity analysis of numerical simulation for CO2geological sequestration in saline aquifers：a case study of Yancheng formation in Subei basin［J］.Journal of Jilin University（Earth Science Edition），2014，44（1）：310-318.

［15］聂昕.页岩气储层岩石数字岩心建模及导电性数值模拟研究［D］.北京：中国地质大学，2014. NIE Xin.Digital core modeling and numerical study of electrical conductivity of shale gas reservoir rock［D］.Beijing：China University of Geosciences，2014.

［16］杨浩，郑秀华，李江，等.巴麦区块泥盆系超低渗储层敏感性试验研究［J］.石油天然气学报，2011，33（9）：116-118. YANG Hao，ZHENG Xiuhua，LI Jiang，et al.Experimental study of sensitivity of ultralow permeability reservoir for devonian system of Bachu-Maigaiti block［J］.Journal of Oil and Gas Technology，2011，33（9）：116-118.

（编辑潘晓慧杨新玲）

Analysis on Sensitivity of Influencing Factors of Rock Electrical Properties Based on the Orthogonal Analysis

DONG Huaimin，SUN Jianmeng，YAN Weichao，CUI Likai
（School of Geosciences，China University of Petroleum，Qingdao，Shandong 266580，China）

Based on the analysis of influencing factors of rock electrical properties，this paper proposes using orthogonal analysis to identify sensitivities of the influencing factors，using orthogonal matrix design to analyze horizontal associations of the influencing factors，and using variance component and trend analysis approaches to quantitatively evaluate the sensitivities by which dominant and secondary factors can be distinguished.Case study from selected core samples shows that rock electrical properties exhibit different sensitivities to different influencing factors，and the sensitivity analysis result is in accordance with that of the numerical simulation of rock electrical properties.

rock electrical property；sensitivity analysis；orthogonal analysis；variance component analysis；trend analysis approach；influ encing factor

TE112.23

A

1001-3873（2016）04-0484-05

10.7657/XJPG20160419

2016-01-07

2016-05-16

国家自然科学基金（41574122；41374124）

董怀民（1993-），男，辽宁建昌人，硕士研究生，地质资源与地质工程，（Tel）18354201362（E-mail）sdsddhm@126.com