基于数字岩心的砂粒对储集层渗透特性影响

薛健康，王玉斗，王殿生，周　伟，王雪英



基于数字岩心的砂粒对储集层渗透特性影响

薛健康，王玉斗，王殿生，周伟，王雪英

（中国石油大学理学院，山东青岛266580）

正确认识砂粒对储集层渗透特性影响，对砂砾岩油藏的合理开采具有重要的意义。基于岩心CT扫描图像，通过砂粒嵌入法构建砂砾岩数字岩心，运用最大球法提取相应的孔隙网络模型，利用逾渗理论研究砂粒对砂砾岩渗透率和残余油饱和度的影响。结果表明，砂粒的存在会降低岩心渗透率，增大残余油饱和度；随着砂粒位置向岩心出口端移动，岩心渗透率逐渐降低，残余油饱和度逐渐减小；砂粒的增大会阻断较多孔隙的连通性，使岩心渗透率降低，残余油饱和度升高；在此基础上建立了岩心渗透率、残余油饱和度与微观孔隙结构参数关系模型，模型预测结果与逾渗模拟结果一致性较好，岩心渗透率相对误差小于7.6%，残余油饱和度相对误差小于2.8%.

砂粒；砂砾岩油藏；数字岩心；逾渗理论；渗透率；残余油饱和度

碎屑岩储集层中砂粒的大小、形状、排列方式极大地影响着储集层的渗透特性，特别是砂砾岩储集层。正确认识砂粒大小、分布对油水渗流的影响，对碎屑岩油田的合理开发有着十分重要的意义［1-3］。目前，受技术手段的限制，大多数的研究都是从宏观角度对砂岩粒度分布特征及其对油水渗流的影响进行分析，从微观角度针对砂粒位置、大小对孔隙结构、渗流特征的研究较少。随着数字岩心技术的不断发展，从微观角度出发，研究砂粒对油水在砂岩中的渗透特性的影响成为可能。本文在岩心CT扫描的基础上，通过砂粒嵌入法建立砂岩数字岩心，利用孔隙网络模型统计砂粒对岩心孔隙结构的影响，并利用逾渗理论从微观角度分析砂粒存在对储集层渗透率和残余油饱和度的影响［4-7］。

1　数字岩心的构建

选用克拉玛依油田八区T88724井下侏罗统八道湾组的砂岩岩心进行研究，取心深度1 600 m，岩心中砂粒相对均匀，岩心孔隙度为25.2%，渗透率为4 630 mD.采用Xradia XRM－500型扫描仪对岩心进行切片CT扫描，扫描分辨率为5 μm，直接获得岩心的二维灰度图像，共扫描500张切片。将CT扫描得到的二维灰度图像经过滤波处理去除图像中的系统噪声，然后选择合适的阈值对孔隙度进行约束，由灰度图像得到相应的二值化图像，利用二维切片的二值化图像重建得到三维数字岩心。在此基础上利用代表体积元法（REV），选取合适尺寸的数字岩心，使其物理性质既不受岩石尺寸的影响又提高了运算效率。本文构建的数字岩心像素数300 pixel×300 pixel×300 pixel，物理尺寸为1.5 mm×1.5 mm×1.5 mm（图1）。为定量研究砂粒对储集层孔隙结构及渗透特性的影响，在此数字岩心上手动嵌入形状规则（长方体）的砂粒（图1），研究砂粒位置、大小等因素对岩心渗透特性的影响［8-9］。

图1　基于T88724井砂岩数字岩心（单位，mm）

2　孔隙网络模型的建立

由于数字岩心无法直接对孔隙结构进行定量描述，而且在数字岩心基础上进行渗流模拟的计算量非常大，因此，采用文献［10］提出的最大球算法，提取拓扑结构和几何特征，利用与数字岩心相同的孔隙网络模型，进行实验模拟。

对于孔隙空间的每一个孔隙体素，采用扩张算法，以每一个孔隙体素为球心向四周延伸，直至找出距孔隙体素最近的骨架体素为止。采用收缩算法，确定孔隙体素对应的内切球，计算内切球的半径上限和下限。孔隙体素对应的内切球集合为

由此得到的内切球集合中，根据内切球的半径上限和下限对其进行删除，得到最大球集合，将孔隙空间的体素表示转换为最大球集合表示。最大球集合没有冗余信息，可以表示整个数字岩心的孔隙空间。在最大球集合中，根据半径以及相邻最大球的重叠部分，进行孔隙喉道划分，这样便形成一个最大球多簇。多簇中半径最大的球体定义为根节点，表示孔隙。假设在一个最大球多簇中存在1个具有2个根节点的球体，那么定义此公共最大球为顶节点，表示喉道，文献［11］将喉道长度定义为总喉道长度与相邻两孔隙长度之差。由于岩心模型中孔喉截面的形状规则，而网络模型为了简化，引入形状因子G.

根据形状因子G（0～0.080）将孔喉截面形状分为3种［12］，即三角形（0～0.048）、正方形（0.048～0.071）和圆形（0.071～0.080）。在数字岩心的基础上，提取了相应的孔隙网络模型（图2）。由孔隙网络模型得到岩心孔隙度为24.6%，渗透率为4 500 mD，与实际岩心测试数据较为吻合，孔隙结构参数如表1所示。

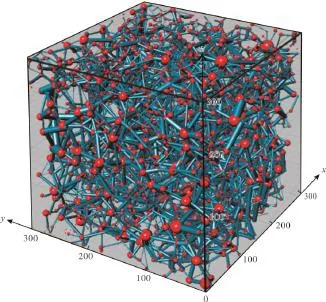
图2　基于T88724井砂岩孔隙网络模型（单位，pixel）

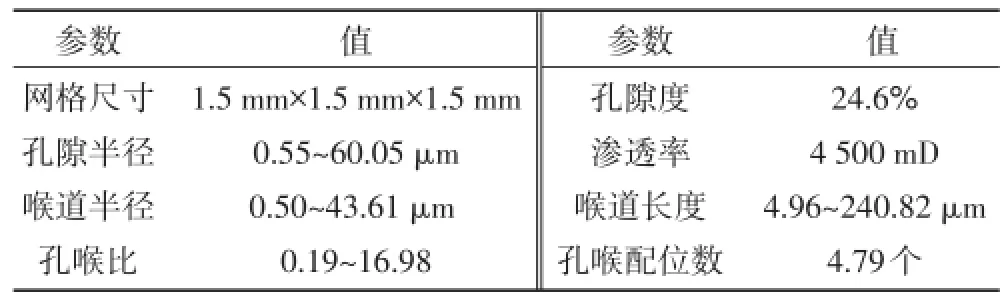
表1　基于T88724井砂岩孔隙网络模型孔隙结构参数

3　油水两相渗流微观模拟

运用逾渗理论模拟孔隙网络模型中的油水两相渗流。假设流体不可压缩、互不相溶，流动过程主要受毛细管压力控制［13］。为消除末端效应，网络中间部分为模拟微观渗流过程以及求解宏观参数的测试区。开始时，岩心孔隙与喉道中充满水，且具有强亲水性，模拟油藏最初的沉积环境，采用Morrow的润湿滞后模型描述岩石润湿性。然后，进行油驱水过程模拟成藏的过程，从一端注入油，逐步增大油相的注入压力，油相进入岩心，水相被驱替，直至模型中的含水饱和度降到设定值15%时，结束油驱水过程［14-16］。在整个油驱水过程中，原油是以活塞式驱替向前推进，由于岩石是水湿的，油相占据喉道单元的中央部分。油驱水过程中，部分孔隙的润湿性发生改变，采用Kovscek的孔隙尺度润湿性转变理论模型。最后，进行水驱油，模拟实际油田开发中注水开采过程。由于油驱水过程结束后，部分孔隙表面的润湿性发生了改变，在部分角隅中残留有水，因此水驱的动力学机制较为复杂。运用活塞式排驱、孔隙体填充以及俘获驱替方式［17-18］，模拟孔隙网络中水驱油过程。

（1）饱和度的计算方法在孔隙网络模型中，组成单元为规则的几何柱体，便于计算出每一个孔喉单元中的含水量和孔隙体积，岩心含水饱和度［4］为

同理，可计算含油饱和度及残余油饱和度。

（2）渗透率的计算方法渗透率可以通过达西定律求解。首先将孔隙网络模型饱和单相流体，然后在孔隙网络模型的两端施加压差（pin-pout），统计出口端的流量，然后代入达西公式，即可计算渗透率，计算公式［4］为

4　模拟计算与结果分析

4.1砂粒位置对岩心渗透特性的影响

为了研究砂粒位置对岩心渗透特性的影响，将像素数为60 pixel×60 pixel×300 pixel的大砂粒嵌入上述数字岩心流动方向的中心线上，通过改变砂粒的位置，讨论砂粒对岩心渗透率和驱油效果的影响。图3显示砂粒中心位置对岩心渗透率影响（图中位置为0对应的数据表示未加入砂粒时的岩心渗透率，即原始岩心渗透率）。可以看出，砂粒的存在对岩心的渗透特性影响较大，渗透率从原来的4 500 mD降低为3 500～4 000 mD.正是由于砂粒的存在阻断了部分孔隙的连通，降低了岩心的孔喉配位数与平均孔喉半径（表2），增大了流体的渗流阻力，渗透率降低。随着砂粒位置向出口端移动，岩心渗透率略有下降，但整体变化幅度不大。说明砂粒的存在降低了岩心渗透率，但砂粒位置对岩心渗透特性影响较小。

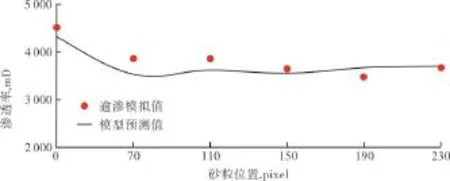
图3　砂粒位置对渗透率的影响

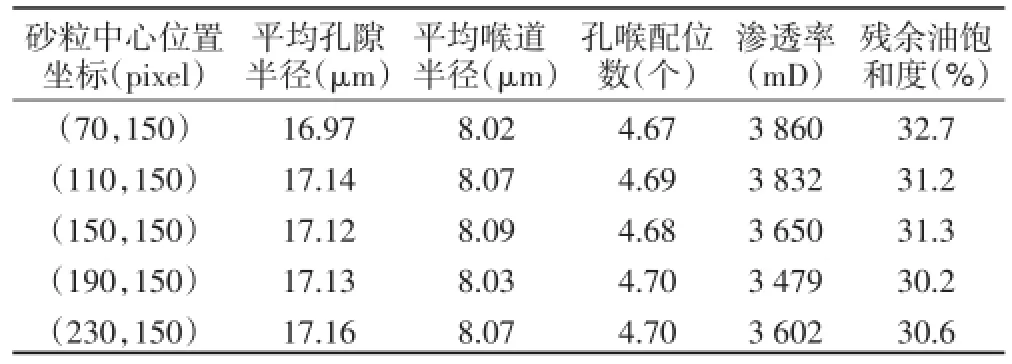
表2　砂粒位置不同时岩心孔隙微观统计参数

从砂粒的位置对残余油饱和度的影响可以看出（图4），砂粒的存在使得岩心残余油饱和度增加，岩心残余油饱和度从不含大砂粒的28.7%升高到32.7%.砂粒的存在，阻断了孔隙间的连通性，改变了孔隙间的流场分布，使得砂粒周围孔隙的原油难以被驱替，残余油增多。随着砂粒位置逐渐靠近出口端，残余油饱和度有逐渐减小的趋势。

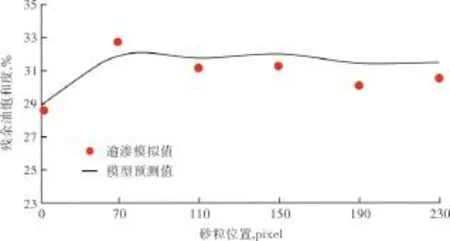
图4　砂粒位置对残余油饱和度的影响

4.2砂粒截面大小对岩心渗透特性的影响

在上述数字岩心的中心位置嵌入像素数分别为60pixel×60pixel×300pixel，80pixel×80pixel×300pixel，100 pixel×100 pixel×300 pixel，120 pixel×120 pixel× 300 pixel的砂粒，研究砂粒水平截面大小对岩心渗透特性的影响（图5）。随着砂粒截面的不断增大，岩心渗透率明显减小，说明砂粒的截面越大，岩心渗流通道被阻断的越多，渗透率越低。

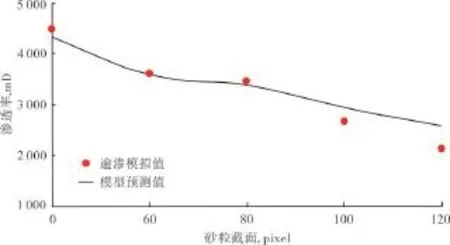
图5　砂粒截面对渗透率的影响

从图6可看出，随着砂粒截面的不断增大，岩心的残余油饱和度呈线性增加。砂粒截面的不断增大阻碍了流体的渗流通道，使得孔隙中越来越多的油无法被驱替出来。

图6　砂粒截面对残余油的影响

4.3砂粒的长度对岩心渗透特性的影响

在上述岩心中心位置处嵌入像素数分别为80 pixel×80 pixel×100 pixel，80 pixel×80 pixel×150 pixel，80 pixel×80 pixel×200 pixel，80 pixel×80 pixel×250 pixel，80 pixel×80 pixel×300 pixel的砂粒，研究砂粒长度对岩心渗透特性的影响（图7），随着砂粒在纵向的长度增加，渗透率降低，说明砂粒在纵向上越长，越多孔隙的连通性被阻断，岩心的渗透特性变差。图8为砂粒长度对残余油饱和度的影响。随着砂粒长度的增加，残余油饱和度有小幅度提高，说明随着越来越多的孔隙连通性变差，其中的原油不容易被驱替，残余油饱和度提高。

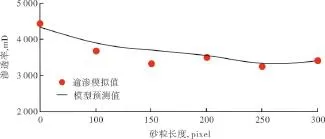
图7　砂粒长度对渗透率的影响

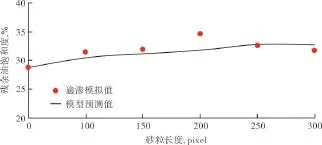
图8　砂粒长度对残余油饱和度的影响

4.4砂粒对岩石渗透特性影响的微观分析及模型建立

砂粒的存在改变了岩心渗透率和残余油饱和度，其根本原因是砂粒的存在改变了岩心微观孔隙结构。表2、表3、表4分别统计出了砂粒位置、截面大小及长度不同时，岩心的平均孔隙半径、平均喉道半径和孔喉配位数等微观孔隙参数，及对应的岩心渗透率和残余油饱和度（原始岩心平均孔隙半径为17.22 μm、平均喉道半径8.11 μm、孔喉配位数4.79个、绝对渗透率4 500 mD、残余油饱和度28.7%）。从微观孔隙结构来看，数字岩心的孔隙结构具有非均匀分布特征，所以无论砂粒位置、大小的变化都会引起孔隙微观参数的变化。数据表明，砂粒的存在降低了平均孔隙半径、平均喉道半径及孔喉配位数。因为砂粒体积在整个数字岩心中所占比例偏小，所以随着砂粒位置、大小的变化，孔隙微观参数有小幅改变。

（1）岩心渗透率与微观孔隙结构参数关系模型

砂粒的存在改变了岩心微观孔隙参数，从而导致渗透率、残余油饱和度随之发生变化。通过分析岩心渗透率与微观孔隙参数之间的关系，建立数字岩心渗透率与微观孔隙结构参数关系模型

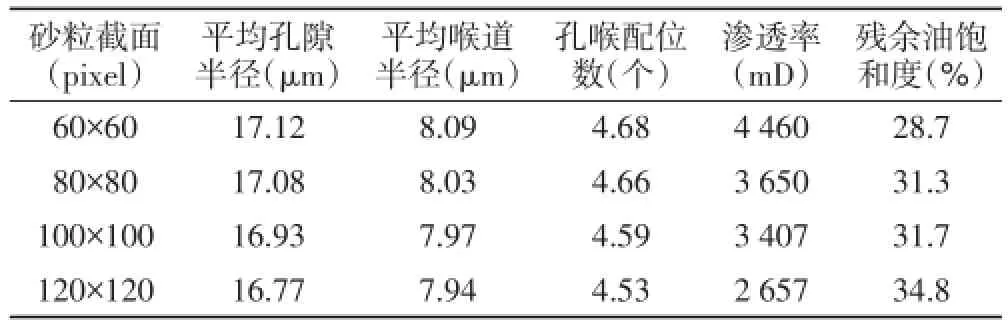
表3　砂粒截面不同时岩心孔隙微观统计参数

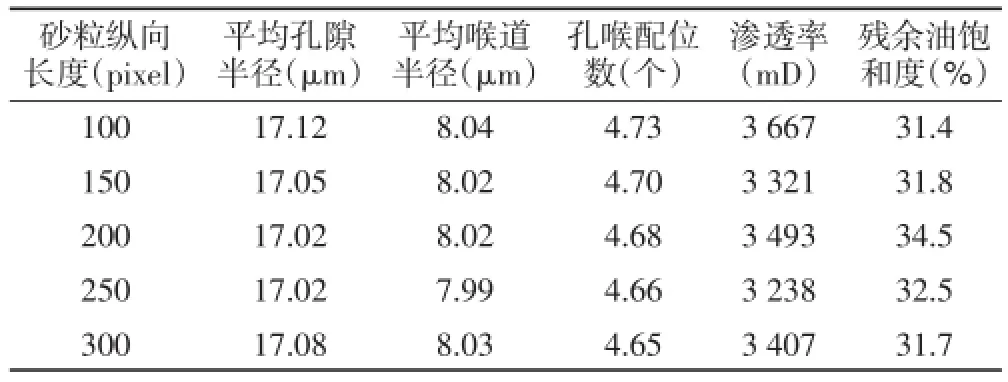
表4　砂粒长度不同时岩心孔隙微观统计参数

利用（5）式对表2、表3、表4中的数据进行拟合，得到渗透率模型参数a=37.25，b=9.01，c=-100，l=e=j= 2.砂粒位置、截面大小、长度作用下渗透率的预测曲线分别见图3、图5和图7.其相对误差为

据（6）式，当砂粒位置、截面以及长度变化时，渗透率的逾渗模拟值与模型预测值之间的相对误差分别为σP（position）=4.8%，σP（size）=7.6%，σP（length）=4.1%.由于模型是基于孔喉配位数、平均孔隙半径、平均喉道半径构建的，而没有考虑其他微观参数（如孔喉比、孔喉体积等）对渗透率的影响，因此模型预测值与逾渗模拟值之间存在一定误差。通过计算可看出，其相对误差值较小，表明此模型较好地反映了当砂粒位置、截面、长度变化时，岩心渗透率的模型预测曲线与逾渗模拟结果拟合很好。

（2）岩心残余油饱和度与微观孔隙结构参数关系模型与渗透率模型类似，建立数字岩心残余油饱和度与微观孔隙结构参数关系模型

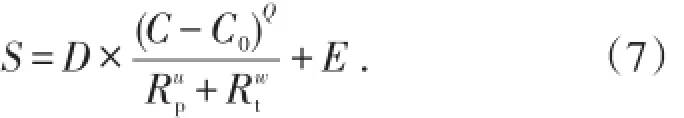
利用（7）式对表2、表3、表4数据进行拟合，残余油饱和度参数D=0.582，Q=4，E=0.36，u=w=2，得到不同砂粒位置、截面、长度下残余油饱和度的预测曲线（图4、图6和图8）。与（6）式类似，当砂粒位置、截面大小以及长度变化时，残余油饱和度的逾渗模拟值与模型预测值之间的相对误差分别为σS（position）=2.5%，σS（size）=2.7%，σS（length）=2.8%.可以看出，模型预测曲线与逾渗理论的模拟结果拟合很好，说明此模型很好地反映了微观孔隙参数对残余油饱和度的影响。

5　结论

（1）砂粒的存在使得岩心渗透率从4 500 mD降低到3 500～4 000 mD，随着砂粒位置向岩心出口端移动，岩心渗透率逐渐降低；大砂粒的存在使残余油饱和度从原始的28.7%升高到32.7%，随砂粒位置向岩心出口端移动，砂粒对残余油饱和度的影响减弱。

（2）砂粒的增大会阻断较多的孔隙连通性，砂粒截面积或砂粒长度的增大都会使岩心渗透率降低，残余油饱和度升高。

（3）本文建立的渗透率、残余油饱和度与微观孔隙结构参数关系模型。反映了砂粒存在时，岩心渗透率和残余油饱和度与平均孔隙半径、平均孔喉半径和孔喉配位数有关。

符号注释

a，b，c，l，e，j——渗透率模型参数，无量纲；

A——模型的横截面积，cm2；

AS——孔隙部分的表面积，μm2；

B——内切球集合；

C——岩心孔喉配位数，个；

C0——临界孔喉配位数，一般情况下等于1；

Ci，Rui，Rdi——分别为第i个内切球的球心、半径上限和半径下限，μm；

D，Q，E，u，w——残余油饱和度模型参数，无量纲；

Esi——第i个岩心逾渗模拟值，mD；

Epi——第i个岩心模型预测值，mD；

K——渗透率，mD；

L——模型的长度，cm；

LS——孔隙长度，μm；

V——所有孔隙体素的集合；

VS——孔隙体积，μm3；

Viw，Vi——分别为第i个孔喉单元中水相体积和孔喉单元体积，μm3；

m——孔隙体素的总数；

n——孔喉单元总数；

q——在压差（pin-pout）驱动下的总流量，cm3/s；

Rp，Rt——分别表示平均孔隙半径和平均喉道半径，μm；

μ——流体黏度，mPa·s.

［1］姚军，王晨晨，杨永飞，等.一种砂砾岩介质岩心表征的新方法［J］.岩土力学，2012，33（增刊2）：205-208. YAO Jun，WANG Chenchen，YANG Yongfei，et al.A new method for rock core characterization in sandy conglomerate media［J］. Rock and Soil Mechanics，2012，33（Supp.2）：205-208.

［2］李庆昌，吴虻，赵立春，等.砾岩油田开发［M］.北京：石油工业出版社，1997：77-82. LI Qingchang，WU Meng，ZHAO Lichun，et al.Development of conglomerate oil field［M］.Beijing：Petroleum Industry Press，1997：77-82.

［3］张丽艳.砂砾岩储层孔隙度和渗透率预测方法［J］.测井技术，2005，29（3）：212-215. ZHANG Liyan.Porosity and permeability predictions in sand-conglomerate reservoir from conventional well logs［J］.Well Logging Technology，2005，29（3）：212-215.

［4］VALVATNE P H.Predictive pore-scale modelling of multiphase flow［D］.London：Imperial College，2004.

［5］高慧梅，姜汉桥，陈民锋.储层孔隙结构对油水两相相对渗透率影响微观模拟研究［J］.西安石油大学学报（自然科学版），2007，22（2）：56-59. GAO Huimei，JIANG Hanqiao，CHEN Minfeng.Simulation study on the effect of the microscopic parameters of reservoir pore structure on oil-water relative permeability［J］.Journal of Xi'an Shiyou University（Natural Science Edition），2007，22（2）：56-59.

［6］李振泉，侯健，曹绪龙，等.储层微观参数对剩余油分布影响的微观模拟研究［J］.石油学报，2005，26（6）：69-73. LI Zhenquan，HOU Jian，CAO Xulong，et al.Microscopic simulation for influence of microscopic reservoir parameters on remaining oil distribution［J］.Acta Petrolei Sinica，2005，26（6）：69-73.

［7］张顺康.水驱后剩余油分布微观实验与模拟［D］.山东东营:中国石油大学，2007. ZHANG Shunkang.The Microscopic experiments and modeling for residual oil distribution after water flooding［D］.Dongying，Shandong：China University of Petroleum，2007.

［8］赵秀才.数字岩心及孔隙网络模型重构方法研究［D］.山东东营:中国石油大学，2009. ZHAO Xiucai.Numerical rock construction and pore network extraction［D］.Dongying，Shandong：China University of Petroleum，2009.

［9］闫国亮，孙建孟，刘学锋，等.储层岩石微观孔隙结构特征及其对渗透率影响［J］.测井技术，2014，38（1）：28-32. YAN Guoliang，SUN Jianmeng，LIU Xuefeng，et al.Characterization of microscopic pore structure of reservoir rock and its effect on permeability［J］.Well Logging Technology，2014，38（1）：28-32.

［10］ØREN P E，BAKKE S.Reconstruction of Berea sandstone and pore -scale modelling of wettability effects［J］.Journal of Petroleum Science and Engineering，2003，39（3）：177-199.

［11］HU Dong.Micro-CT imaging and pore network extraction［D］.London：Imperial College，2007.

［12］MASON G，MORROW N R.Capillary behavior of a perfectly wetting liquid in irregular triangular tubes［J］.Journal of Colloid and Interface Science，1991，141（1）：262-274.

［13］刘生丽，冯辉霞，张建强，等.逾渗理论的研究及应用进展［J］.应用化工，2010，39（7）：1 074-1 078. LIU Shengli，FENG Huixia，ZHANG Jianqiang，et al.The research of percolation theory and application［J］.Applied Chemical Industry，2010，39（7）：1 074-1 078.

［14］陶军，姚军，李爱芬，等.利用孔隙级网络模型研究油水两相流［J］.油气地质与采收率，2007，14（2）：74-77. TAO Jun，YAO Jun，LI Aifen，et al.Research on oil and water flow using pore-scale network model［J］.Petroleum Geology and Recovery Efficiency，2007，14（2）：74-77.

［15］侯健，李振泉，张顺康，等.岩石三维网络模型构建的实验和模拟研究［J］.中国科学G辑：物理学力学天文学，2008，38（11）：1 563-1 575. HOU Jian，LI Zhenquan，ZHANG Shunkang，et al.Rock 3-D network model building of experiment and simulation study［J］.Science in China Series G：Physics，Mechanics&Astronomy，2008，38（11）：1 563-1 575.

［16］VALVATNE P H，BLUNT M J.Predictive pore-scale modeling of two-phase flow in mixed wet media［J］.Water Resources Research，2004，40（7）：1-21.

［17］LENORMAND R，TOUBOUL E，ZARCONE C.Numerical models and experiments on immiscible displacements in porous media［J］. Journal of Fluid Mechanics，1988，189：165-187.

［18］LENORMAND R，ZARCONE C，SARR A.Mechanisms of the displacement of one fluid by another in a network of capillary ducts［J］.Journal of Fluid Mechanics，1983，135：337-353.

（编辑曹元婷）

Impact of Sand Grains on Reservoir Permeability Based on Digital Cores

XUE Jiankang，WANG Yudou，WANG Diansheng，ZHOU Wei，WANG Xueying
（School of Science，China University of Petroleum，Qingdao，Shandong 266580，China）

Accurate understanding of the effect of sand grains on reservoir permeability is significant for reasonable development of sandy conglomerate reservoirs.On the basis of CT scanning images of cores，digital cores of sandy conglomerate are constructed with sand-grain imbedding method，the corresponding pore network model is extracted with the maximum ball method and the impact of sand grains to permeability and residual oil saturation of sandy conglomerate is studied using percolation theory.The result shows that the existence of sand grains will decrease core permeability and increase residual oil saturation；with sand grains moving towards core outlet end，core permeability and residual oil saturation will gradually decrease；the increase of sand grain size will block flow paths among pores，which will result in the decline of core permeability and increase of residual oil saturation.Then a relation model between core permeability and micro-pore structural parameters has been established and the prediction result obtained from the model shows good consistency with the percolation modelling result，the relative errors of core permeability and residual oil saturation are less than 7.6%and 2.8%，respectively.

sand grain；sandy conglomerate reservoir；digital core；percolation theory；permeability；residual oil saturation

TE112.23

A

1001-3873（2016）04-0464-05

10.7657/XJPG20160415

2016-01-05

2016-04-18

国家自然科学基金（51574268）；山东省自然科学基金（ZR2014EEM050）

薛健康（1991-），男，山东青岛人，硕士研究生，油气藏工程，（Tel）13864886298（E-mail）jiankang200823@163.com