基于有限元的三维随机形貌结合面接触分析*

刘海涛　杜虎兵　王建华

(西安工业大学机电工程学院，陕西 西安 710021)



基于有限元的三维随机形貌结合面接触分析*

国家自然基金面上项目(51475351)；陕西省自然基金面上项目(2015JM5190)

刘海涛杜虎兵王建华

(西安工业大学机电工程学院，陕西 西安 710021)

机加工结合面表面形貌是三维的、随机的，传统的基于微凸体的接触模型由于进行了大量假设，其结论只能在较为苛刻的条件下成立。据结合面三维形貌测量得到的数据，重构出不同材料、加工方式的表面，采用有限元法建立了随机表面的接触模型，通过接触分析来获得了下结合面法向变形量随外载荷的变化规律，并推导出单位面积上结合面法向刚度系数的表达式。结果表明，结合面法向变形量与法向载荷基本符合幂指数函数关系；表面加工方式的不同对于结合面接触性能的影响较大，磨削表面的法向变形量明显小于铣削表面；除铸铁铣削表面外，其他结合面的法向刚度系数趋于稳定，彼此之间相差不大。

结合面；随机形貌；接触分析；有限元法

机床结合面一般是通过铣削、磨削等机械加工方法得到，其显著的特点就是机加工表面形貌是三维的、随机的、符合统计学规律的[1]，且有的表面具有明显的纹理，比如刨削、铣削，在沿着加工方向和垂直于加工方向的凸峰形貌可能会有明显的差别，有的则会形成类似“孤岛”的微凸峰，如研磨。

传统的基于微凸体的接触模型，如Hertz模型[2]、GW模型[3]等，采用经典的接触理论分析两粗糙表面的接触时，进行了大量的假设，如将随机的、复杂粗糙表面简化为两单一的微凸体的接触，以及对于材料弹塑性本构的简化处理等[4-6]，造成其结论只能在较为苛刻的条件下成立，通用性较差。因此，要想使结合面的刚度、阻尼等数据具有较强的普适性，就必须基于结合面具有三维随机形貌这一特性建立模型，在此基础上进行分析。

有限元的方法是解决粗糙表面接触问题的一个有效的手段，其鲁棒性以及强大的自适应能力能够解决复杂的、解析方法难以解决的问题[7]，其建模方法不受表面复杂形貌的约束，且在材料本构的处理上也具有很大的优势。因此，本文根据结合面三维形貌测量的数据重构出不同材料、加工方式的表面，建立基于随机表面的接触模型，通过有限元接触分析来获得粗糙度尺度下结合面法向变形量随外载荷的变化规律，并推导出单位面积上结合面法向刚度系数的表达式。

1　具有随机形貌的结合面表面重构

结合面的形貌虽然是随机的、杂乱无章的，但仍然是符合统计规律的，因而，其接触特性理论上也应该是稳定的、具有统计学意义的。本文采用白光干涉仪对结合面进行测试，利用获得的点云数据，重构出结合面的三维模型。先从外部数据中读入数据点作为节点的z坐标，并按照采样间隔x和y坐标，然后根据坐标(x,y,z)在空间建立节点，将节点连成面就可重构出测量的取样表面，如图1所示。

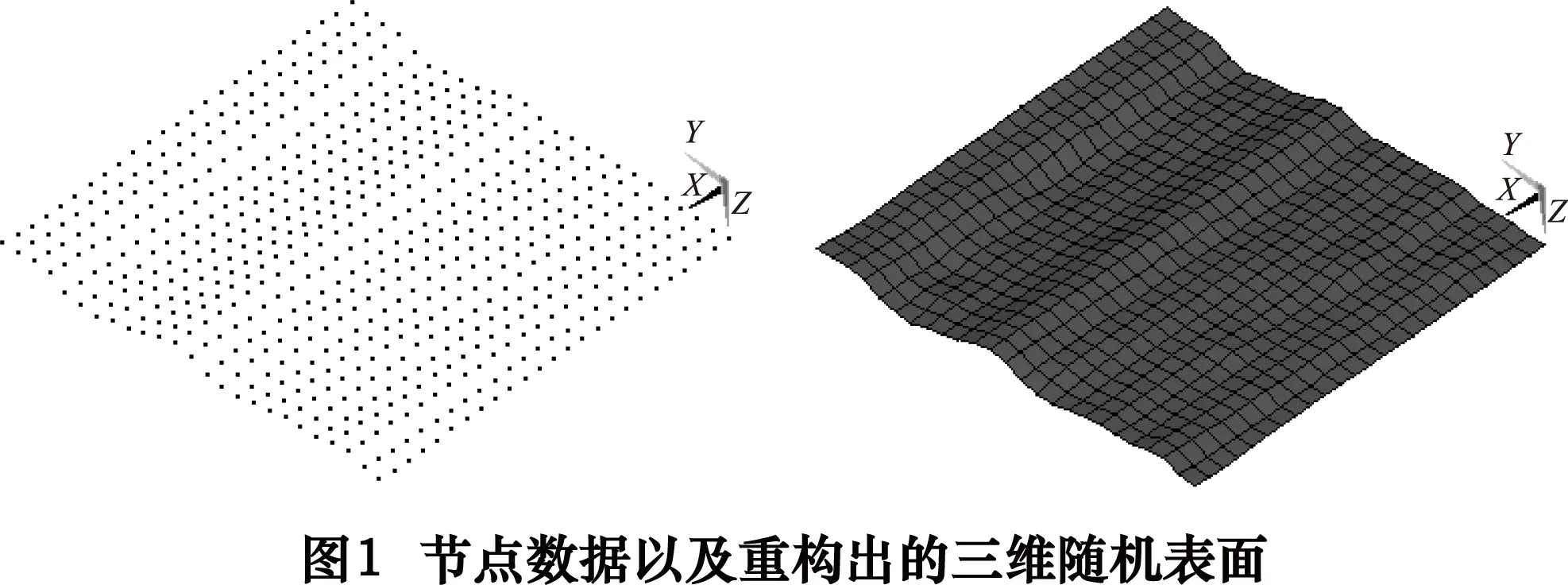
在此基础上建立两层单元，第一层为表面层，此层单元的高度应与取样间隔相近，如果取的过大将造成单元过长，影响计算精度；第二层为基体，基体的高度20 μm。图2～3为在ANSYS[8-11]中重构出的40Cr磨削表面(Ra=1.6 μm)、40Cr铣削表面(Ra=3.2 μm)采用的单元为Solid185八节点单元。取样面积为160 μm×160 μm，取样间隔为6.4 μm，即每隔6.4 μm取1个数据点，因此每个取样表面共包含25×25=625个数据点。45#钢磨削表面(Ra=1.6 μm)和45#钢铣削表面(Ra=3.2 μm)与40Cr磨削表面和40Cr铣削表面相同，这里不再赘述。

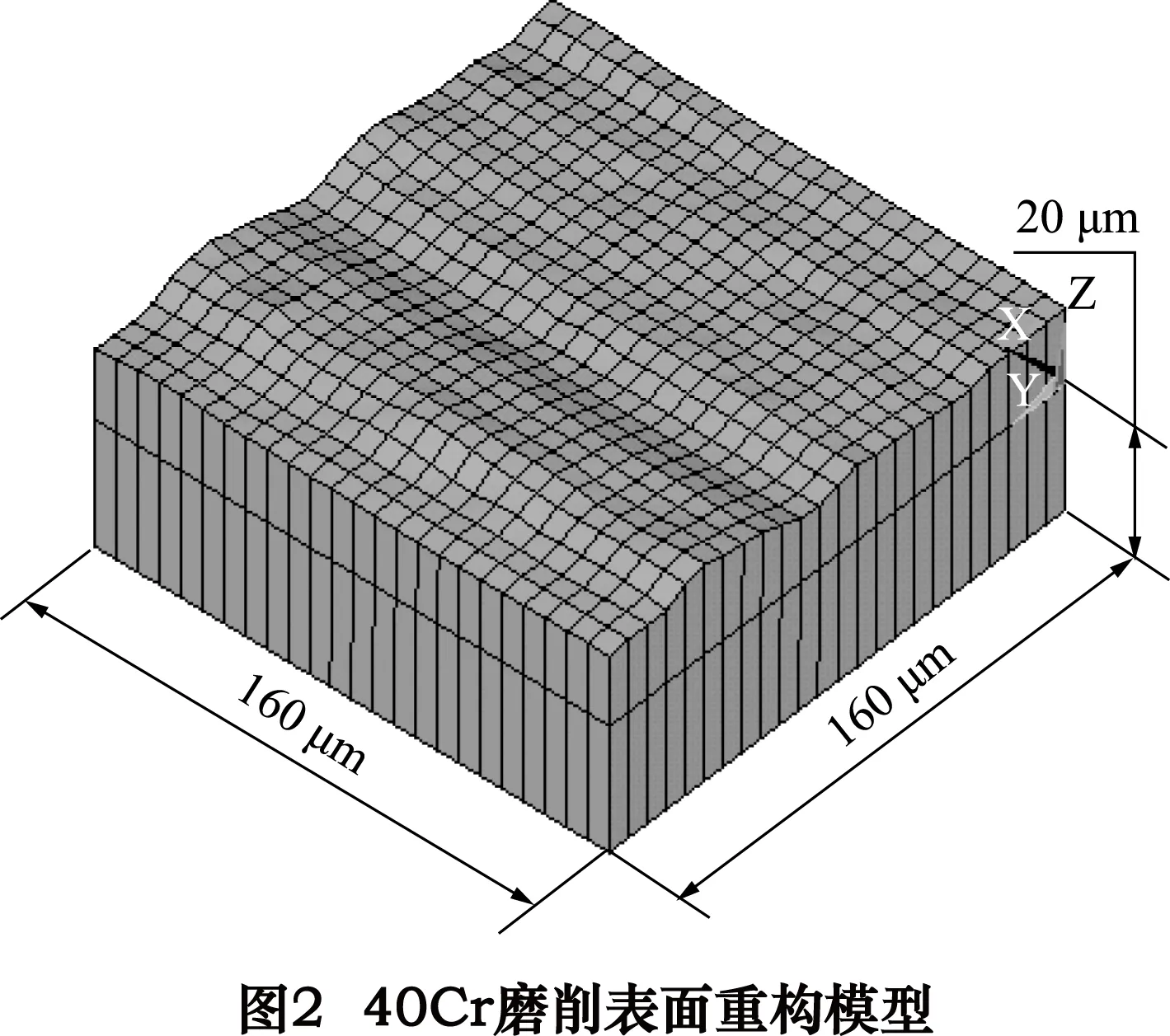
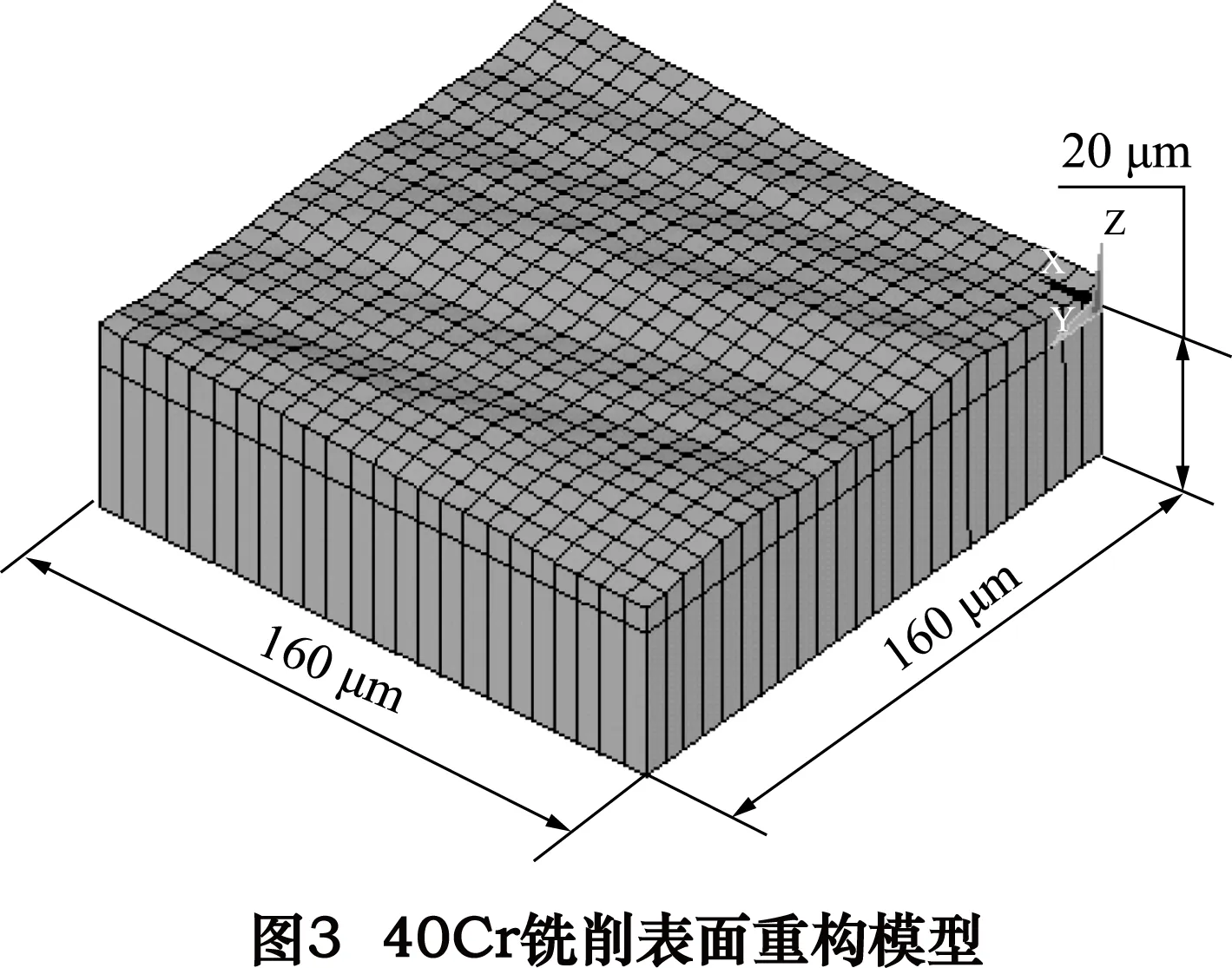
图4为铸铁磨削重构表面(Ra=1.6 μm)，图5为铸铁铣削重构表面(Ra=3.2 μm)，与40Cr和45#钢不同的是其取样间隔为5.12 μm，基体的高度为10 μm，每个取样表面仍然包含625个数据点，则取样面积为128 μm×128 μm。

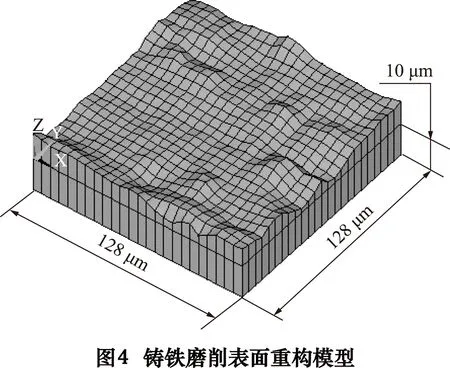
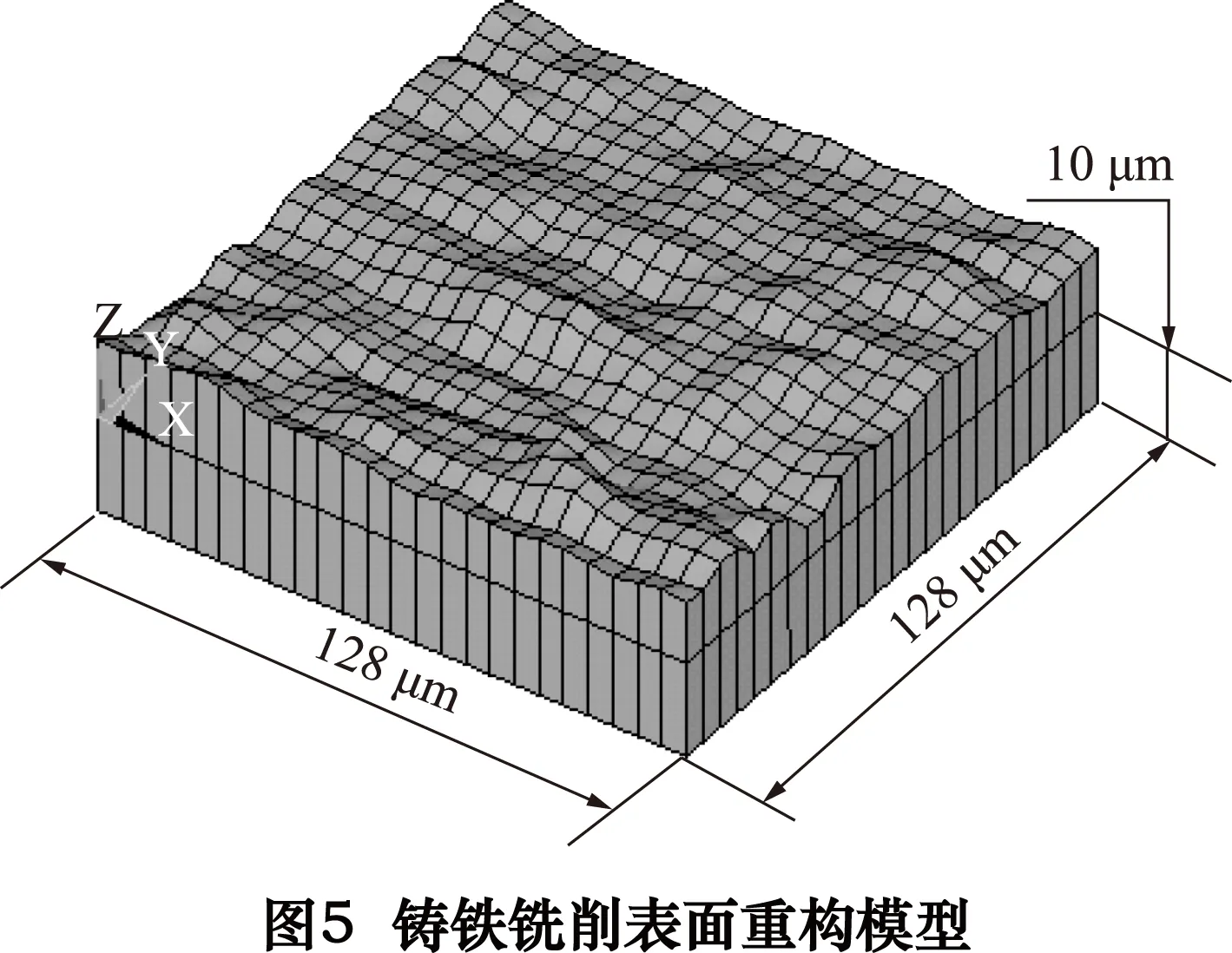
2　基于有限元的三维随机表面接触分析

2.1材料的弹塑性本构

由于结合面接触微凸体在外载荷的压力下不但会发生弹性变形，而且在大载荷下会发生塑性变形，因此如何表征材料的弹塑性属性就显得十分关键。本文采用多线性等向强化模型处理材料的弹塑性问题。多线性随动强化模型使用多线性来表示应力应变曲线，从而模拟随动强化效应。多线性等向强化模型使用多线性来表示使用Von Mises屈服准则的，适用于比例加载的情况及大应变分析，可以涵盖绝大部分的材料本构。

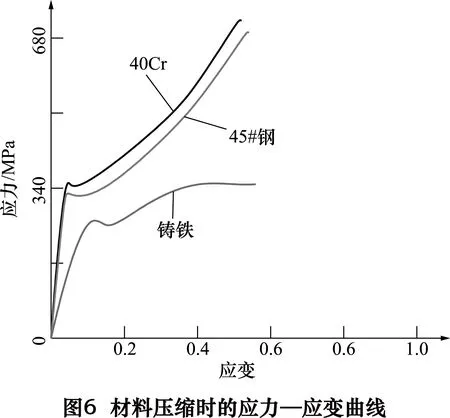
图6为45#钢、40Cr以及铸铁压缩时的应力—应变曲线，可以看出，3种材料应力—应变曲线的拐点不止1个，这是一般的材料本构模型都无法完整地表达的，图7为对应的3种材料多线性等向强化模型。

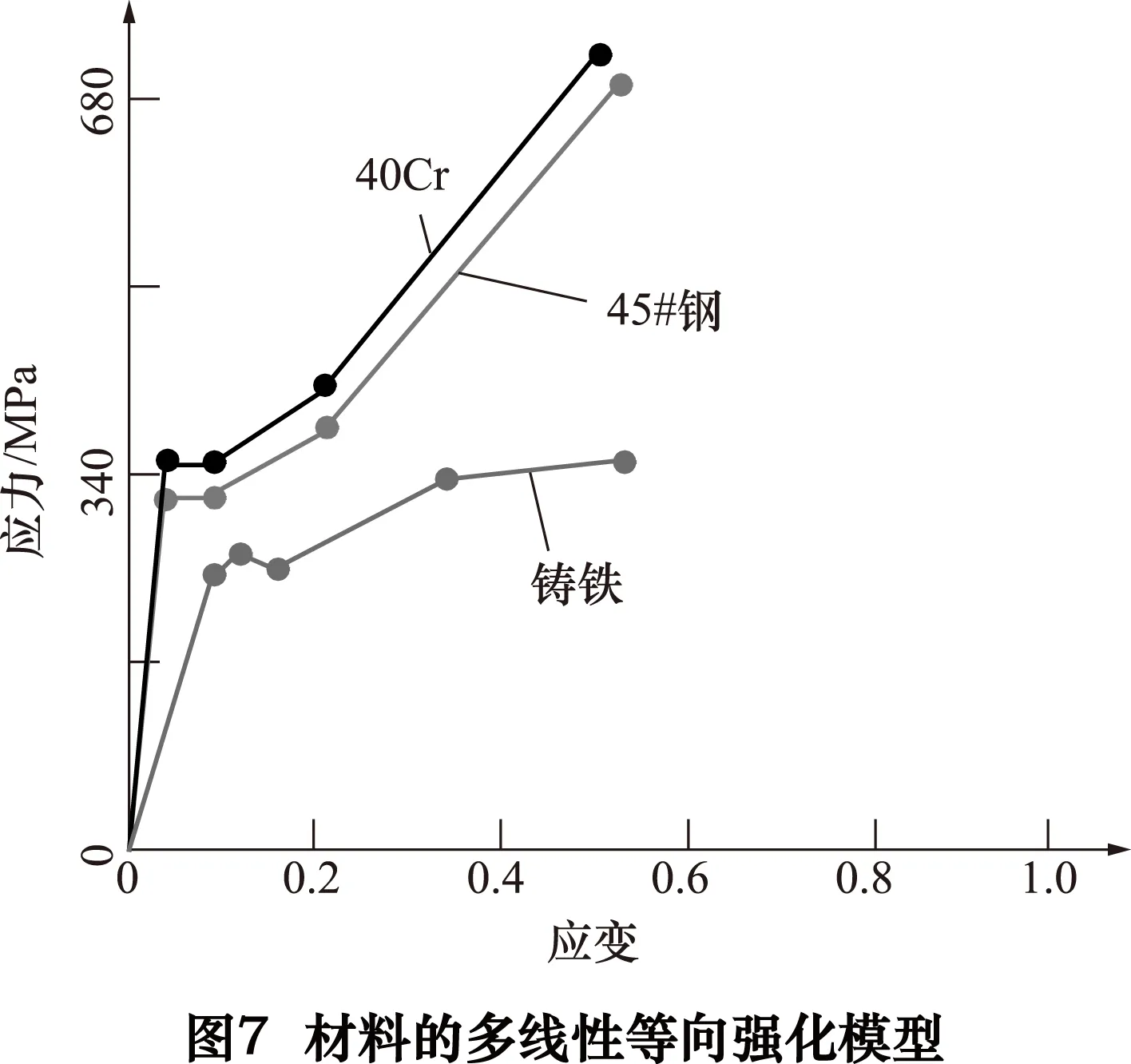
2.2三维随机表面的有限元接触模型的建立

叮铃铃，思雨被一阵电话铃声吵醒。那些美女和她们栗红色的秀发都不见了。电话铃声还在纠缠着响。思雨爬起来，接电话。电话里传来一个娇滴滴的声音：“先生，您好！我叫佳佳，今年20岁，身高1.68，体重48公斤。我特别美的是我有一头栗红色的长发。先生，您需要我的服务吗？”思雨的酒醒了一半，他对着话筒急急地说：“你说什么？你有一头栗红色长发？”话筒里传来了女声说：“是的，先生，我有一头栗红色的美丽的长发，我的长发迷倒了很多靓仔耶！”思雨已到了急不可耐的程度，他不假思索地喊：“好，快，你来我看看。”

本文只讨论两个相同表面之间的接触问题，即结合面材料相同，加工方式相同的情况，材料为上述提到的40Cr、45#钢和铸铁，加工方式为铣削和磨削，因此共有6种不同的表面。

为了使结果具备通用性，每种表面加工3个试件，编号为#1、#2、#3，对其表面进行三维形貌数据的采集，分别对#1和#2、#1和#3以及#2和#3数据点重构出的模型进行接触分析，即每种表面进行3组接触分析。使用Solid185单元定义实体，使用TARGE170单元将上表面设为目标面，使用CONTA174单元将下表面设为接触面。经反复试验，设置FKN=2.5时结果趋于稳定。在上表面基体上施加面载荷，其接触模型及边界条件如图8所示。

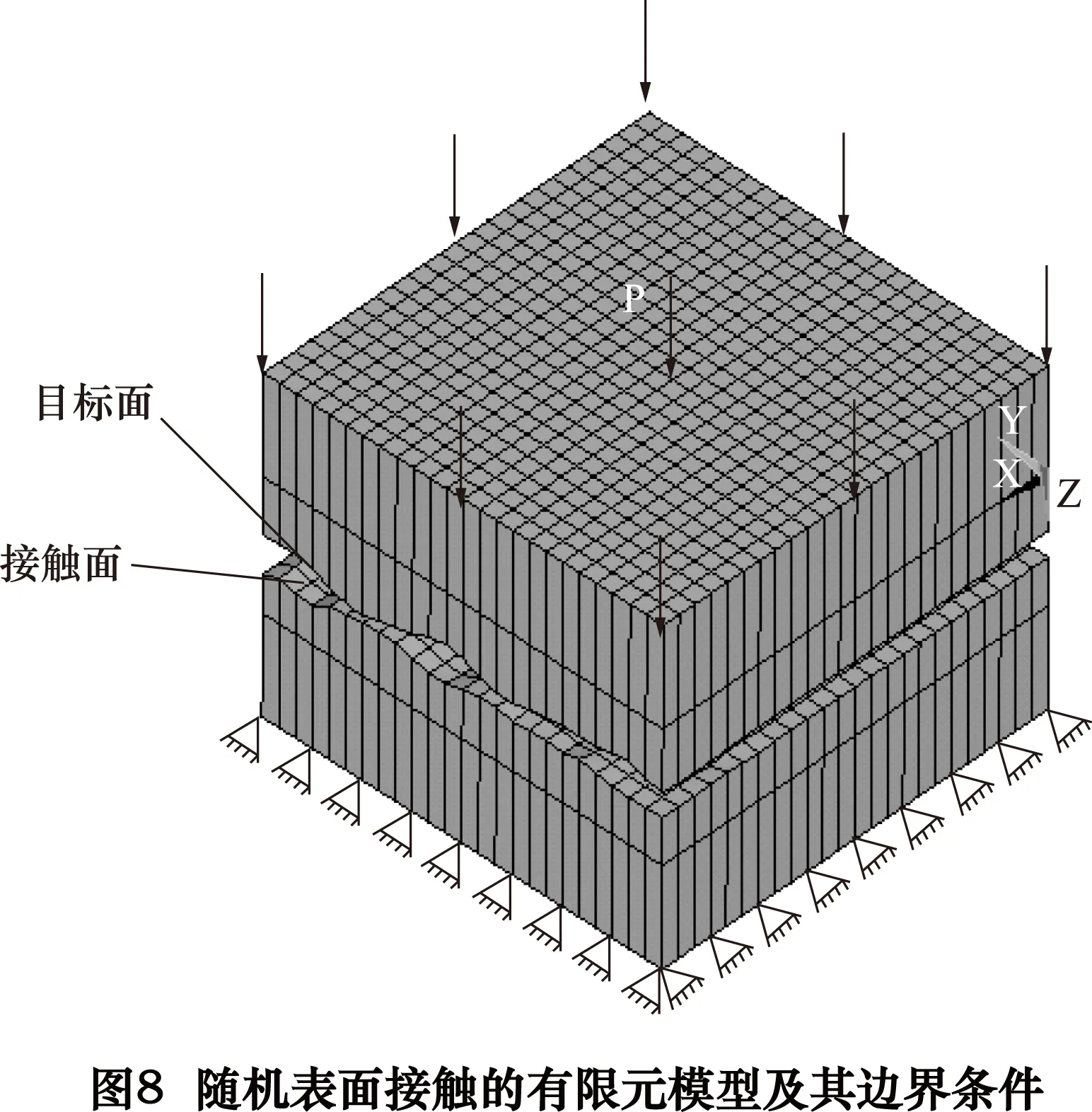
3　结合面接触分析及法向接触刚度的推导

3.1结合面法向变形与法向载荷的关系分析

图9为40Cr磨削和铣削表面结合面法向载荷随法向变形的变化规律。从中可以看出，随着结合面法向变形量的增大，法向载荷也随之增大，变化规律基本符合幂指数函数关系。表面加工方式的不同对于结合面接触性能的影响较大，在施加同等法向外载荷的情况下，磨削表面的法向变形量明显小于铣削表面。例如，在500 MPa的法向载荷下，磨削表面的法向变形为1.5 μm左右，而铣削表面的法向变形则接近2.0 μm。

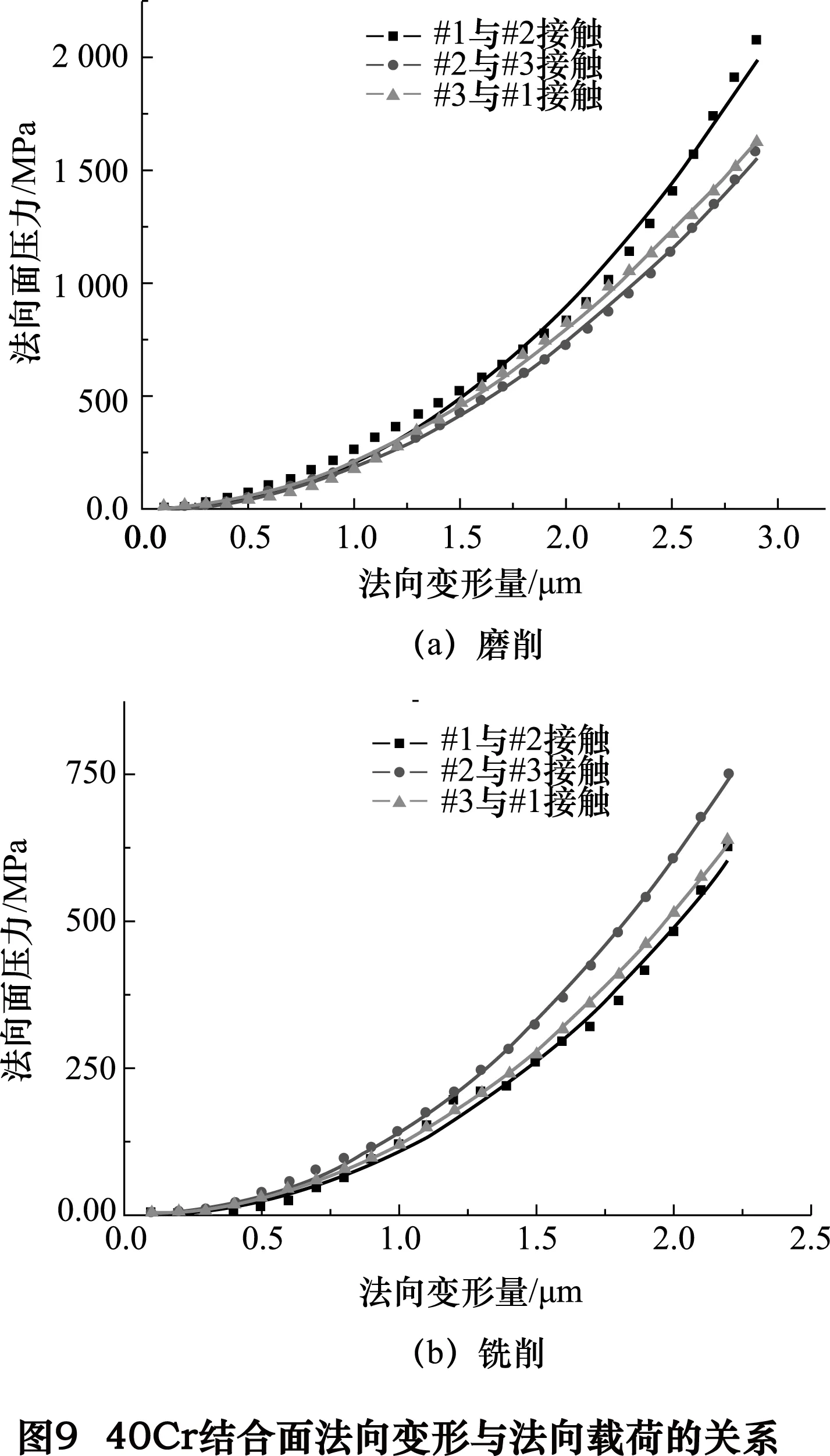
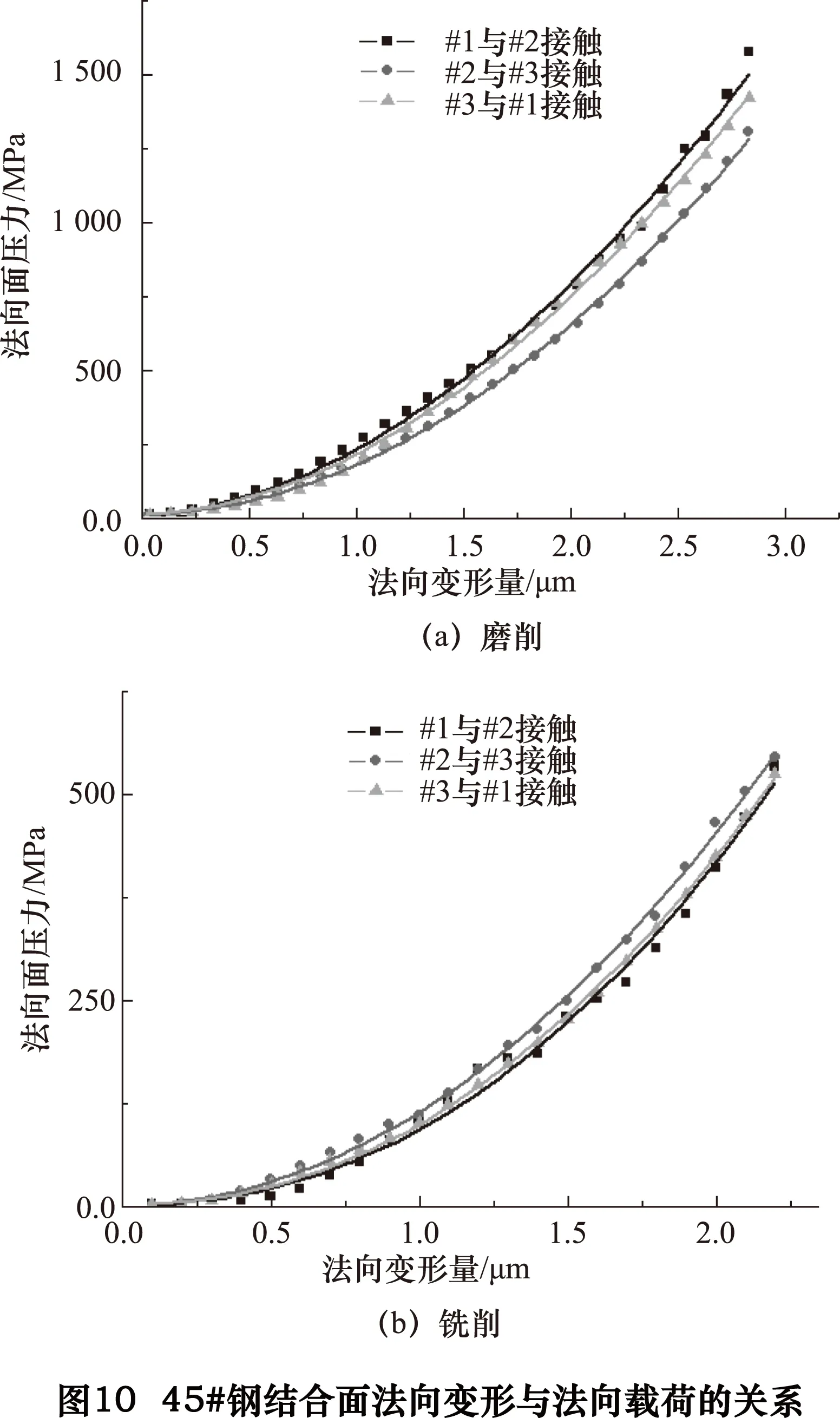
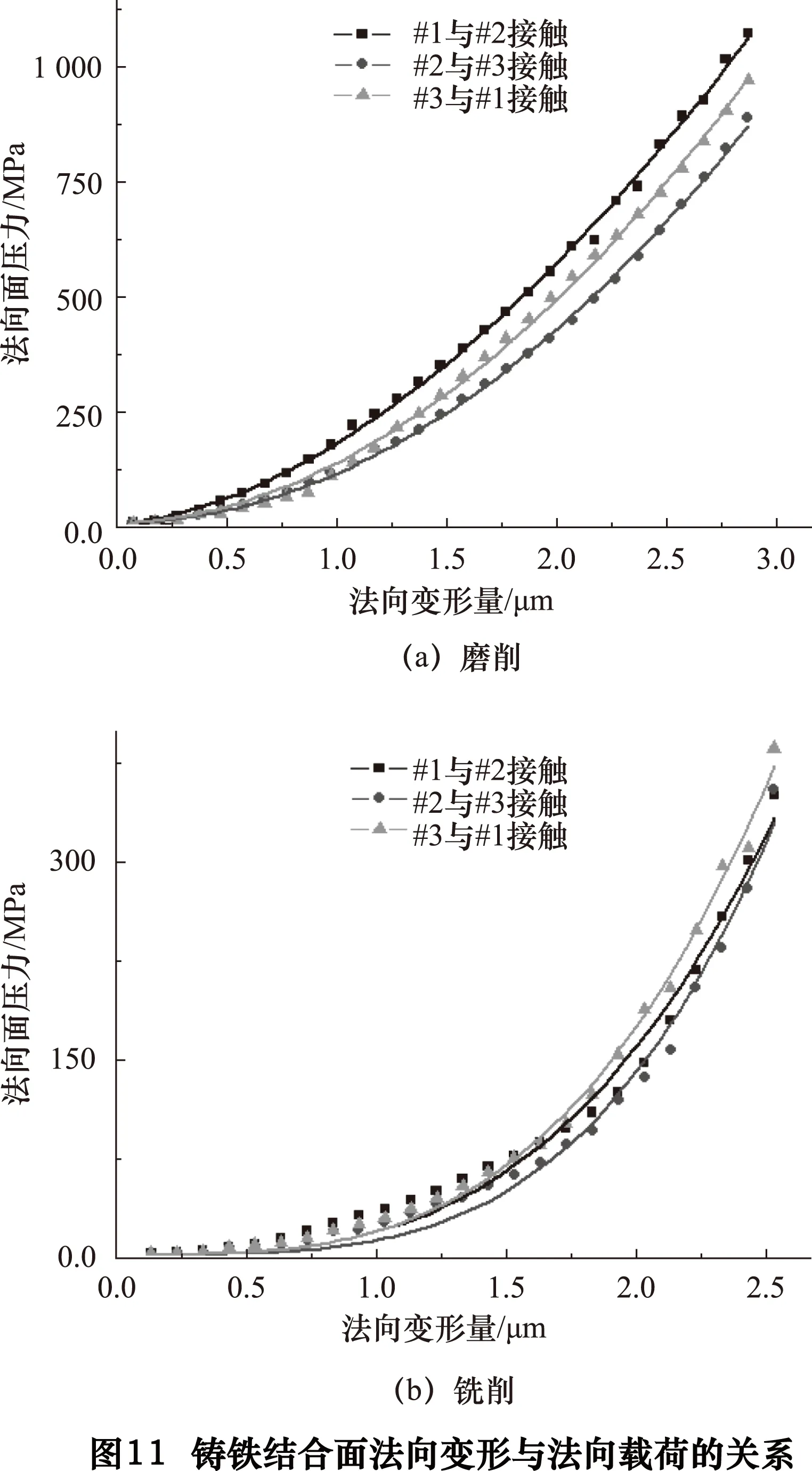
图10为45#钢磨削和45#钢铣削表面结合面法向载荷随法向变形的变化规律。与图9中显示的规律一致，结合面法向变形量与法向载荷基本符合幂指数函数关系。对比图9和图10可知，同一种加工方法下，40Cr在接触性能上要略优于45#钢。铸铁磨削和铣削表面结合面法向载荷随法向变形的变化基本规律与45#钢和40Cr基本相同，如图11所示。

3.2单位面积上结合面法向接触刚度的推导

由经验知识可知，结合面法向变形量与法向载荷存在指数函数关系。即：

Pn=aλb

(1)

图9～11的数据点是按照式(1)的形式进行曲线拟合，得到的常数a和b如表1所示。表中每种表面计算了3组数据，如#1#2代表#1面与#2面接触分析、数据拟合获得的常数，并求取其平均值。

表16种典型机床结合面常数a和b

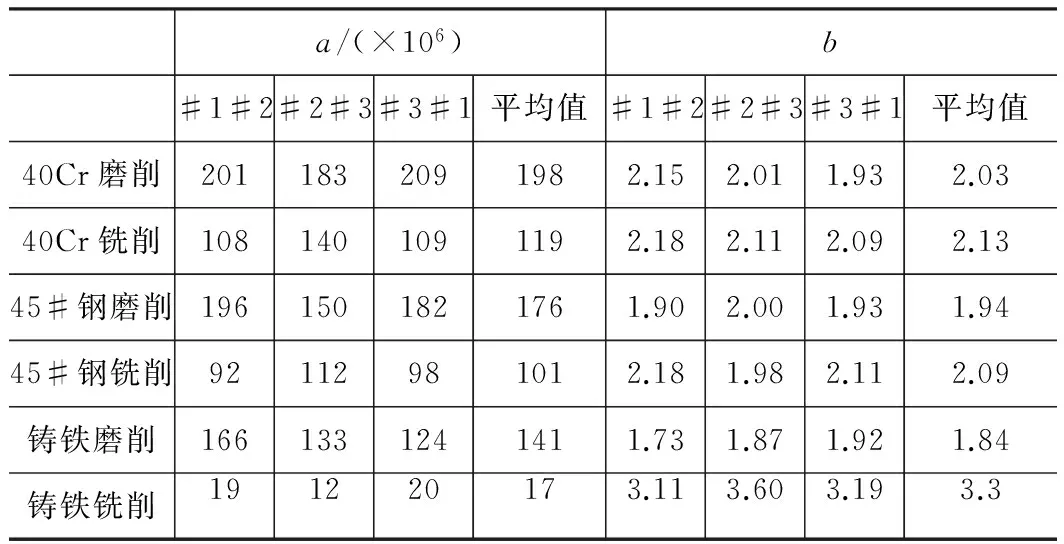
a/(×106)b#1#2#2#3#3#1平均值#1#2#2#3#3#1平均值40Cr磨削2011832091982.152.011.932.0340Cr铣削1081401091192.182.112.092.1345#钢磨削1961501821761.902.001.931.9445#钢铣削92112981012.181.982.112.09铸铁磨削1661331241411.731.871.921.84铸铁铣削191220173.113.603.193.3

式(1)可以变换为如下形式：

(2)

将式(2)对Pn求导可得：

(3)

式(3)的倒数即为结合面法向刚度kn的表达式为

(4)

依据式(4)以及表1中a、b的平均值计算出来的6种机床结合面的法向刚度表达式为：

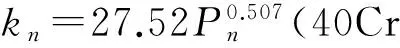
(5)

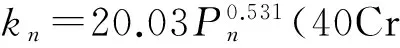
(6)

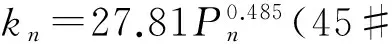
(7)

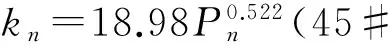
(8)

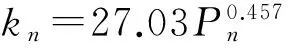
(9)

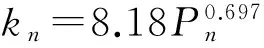
(10)

从式(5)～(10)可以看出，除铸铁铣削表面外，其他结合面的法向刚度系数趋于稳定，彼此之间相差不大，尤其是常数b，稳定在2.0左右。

5　结语

本文采用有限元法对三维随机形貌的结合面进行接触分析，获得了结合面法向变形量随外载荷的变化规律，并推导出单位面积上结合面法向刚度系数的表达式，主要结论如下：

(1)结合面法向变形量与法向载荷基本符合幂指数函数关系。

(2)表面加工方式的不同对于结合面接触性能的影响较大，磨削表面的法向变形量明显小于铣削表面。

(3)除铸铁铣削表面外，其他结合面的法向刚度系数趋于稳定，彼此之间相差不大。

[1]费斌，王海容，蒋庄德．机械加工表面分形特性的研究[J]，西安交通大学学报，1998(5)：83-86．

[2]Hertz H. Uber die Beruhrungfester elastischer Korper (On the contact of elastic solids)[J]. Reine and Angew. Math., 1882, 92: 156-171.

[3]Greenwood J A, Williamson JP. Contact of nominally flat surfaces[J]. Proc. Roy. Soc. (London) A, 1966, 295: 300-319.

[4]Onion RA, Archard JF. The contact of surfaces having a random structure[J]. Phys.D: Appl.Phys, 1973(6): 289-304.

[5]Bush AW, Gibson RD, Thomas TR. The elastic contact of a rough surface[J], Wear, 1975,35: 87-111.

[6]Majumdar A.,Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. J. Tribol(ASME),1991,113:1-11.

[7]陈国荣．有限单元法原理及应用[M]．北京：科学出版社，2009．

[8]张应迁，张洪才．ANSYS有限元分析从入门到精通[M]．北京：人民邮电出版社，2010．

[9]周宁．ANSYS APDL高级工程应用实例分析与二次开发[M]．北京：水利水电出版社，2008．

[10]龚曙光，云清．有限元分析与ANSYS APDL编程及高级应用[M]．北京：机械工业出版社，2009．

[11]龚曙光，谢桂兰．ANSYS操作命令与参数化编程[M]．北京：机械工业出版社，2004．

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Contact analysis of three-dimensional random morphology joint interface based on finite element method

LIU Haitao, DU Hubing, WANG Jianhua

(School of Mechatronic Engineering, Xi'an Technological University, Xi'an 710021, CHN)

The morphology of joint interface obtained by machining process is three-dimensional and random, so that the conclusions which are derived from traditional contact models based on micro-asperity, can only hold true under harshly conditions because of the using of many assumptions. In this paper a contact model of random surfaces based on finite element method is set up and the rules of normal deformation with respect to external load are obtained by contact analysis. The expressions of normal stiffness per unit area of joint interfaces are derived. The results show that an exponential relationship between normal deformation and normal applied load exists; the contact properties of the joint interfaces are significantly influenced by the machining method of the surfaces, and the normal deformation of the surface machined by grinding is obviously less than the surface machined by milling; the normal stiffness coefficients of joint interfaces have no significant difference except the milled cast surface.

joint interface; random morphology; contact analysis; finite element method

TH11

A

10.19287/j.cnki.1005-2402.2016.07.018

刘海涛，男，1981年生，博士，讲师，主要从事机床性能仿真、精密测量、产品流程自动化等方面研究，已发表论文10余篇。

(编辑李静)(2015-12-15)

160727