一种基于双目立体视觉的测量方法*

于　振　刘书桂

(精密测试技术及仪器国家重点实验室(天津大学)，天津 300072)



一种基于双目立体视觉的测量方法*

于振刘书桂

(精密测试技术及仪器国家重点实验室(天津大学)，天津 300072)

以双目立体视觉理论为基础，提出了一种基于射线交汇法的双目模型。标定好双目系统后，使用Harris算法提取图像中的特征点，经过立体匹配，求出特征点在相机坐标系下的三维坐标，从而计算出任意点间的距离，并通过理论推导证明其比另一种双目模型计算出的结果更精确。实验表明该方法能够较精确的对物体实现三维测量。

射线交汇法；双目模型；三维测量

双目立体视觉由于结构灵活、安装方便、成本低而被广泛采用。其作为计算机视觉的一个分支，是利用2台摄像机同时对物体拍照，根据景物点在左右摄像机图像上的位置关系计算出景物点的三维坐标，从而可以实现三维测量和恢复。由于结构简单、数据采集方便迅速、属于非接触式测量,可以应用于各种复杂恶劣的环境中。双目视觉被广泛应用于三维检测、机器人导航、医学成像等领域[1]，物体三维测量一直是人们研究的热点。目前大多数研究集中在摄像机标定[2-3]特征匹配[4-5]及精度分析[6]等方面。为了获得较高的三维测量精度，很多专家学者更是将研究重点放在了特征匹配部分，提出了如快速双边滤波算法[7]、 基于自适应权重的三边滤波算法[8]、迭代优化的自适应权重算法[9]以及二进制立体匹配算法BSM[10]等方法。本文立足于双目测量理论的基础——双目模型，提出了一种基于射线交汇法的简单双目模型，并与另一种基于三角法的双目模型[11]进行了比对。通过误差分析，在理论上证明了基于射线交汇法的双目模型比基于三角法的双目模型有更高的精度，并通过实验以及实验后的结果分析，验证了这一观点。

1　实验装置

1.1摄像机及试验台架

如图1所示，系统采用两台型号参数一致的高分辨率低畸变CCD摄像机,安装在与各摄像机相配的摄像机三脚架上，通过调节摄像机三脚架使两台摄像机之间的间距、夹角及高度可以任意调节，以满足不同的工作距离及有效视场范围的要求。测量误差与两镜头光轴夹角及基线距离间存在复杂的函数关系，在满足工作距离及有效视场的前提下，系统误差随基线距增大而减小，且当基线与光轴的夹角在40°～60°之间取值时，平均综合测量误差达到最小值[12]。

1.2照明光源

如图2所示，系统采用DLP投影仪作为光源。通过设计程序和分屏控制，让投影仪分别投影出不同的图案以方便测量。当对摄像机进行标定时，通过向棋盘格投影白光，从而使各像机像平面上的棋盘格成像更加清晰。当进行测量实验时，可以通过投影不同的图案以方便提取所测物体上的特征点并进行特征匹配，从而对物体三维形貌进行密集测量。

实验采用两台型号参数一致的高分辨率低畸变CCD摄像机进行，为了提高结果的可靠性分别按照图3、图4的方法进行了3组独立重复实验，每次实验中分别使用左、右摄像机各拍摄一幅图像，再转换标定板的摆放方式，继续在左右拍摄点拍摄得到左右图像，依此类推。

2　两种双目模型测量效果比对

2.1基于三角法的双目模型[11]

如图3所示，设左摄像机坐标系与世界坐标系重合，记为OXYZ，左摄像机图像坐标系为OlXlYl，有效焦距为fl；右摄像机坐标系为OrXrYrZr，其图像坐标系为OrXrYr，有效焦距为fr，P点为公共视野内的待测点。

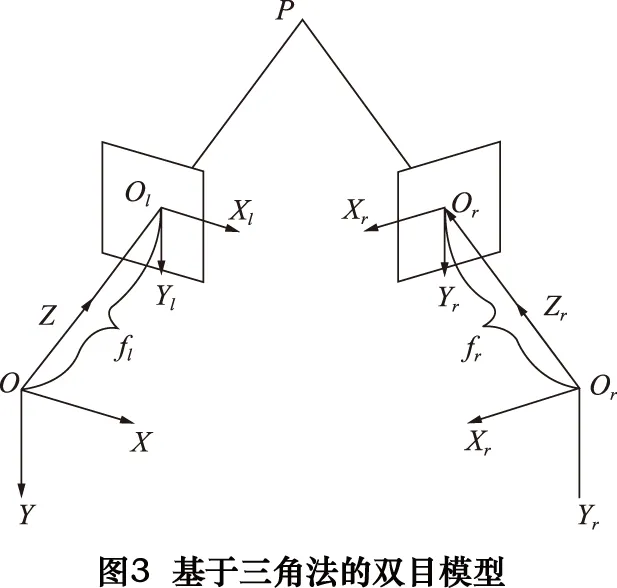
根据摄像机透视变换模型可知，在传感器坐标系下被测点与各摄像机像面点之间的对应变换关系分别为：

(1)

(2)

当左摄像机与世界坐标系重合时，设左摄像机有效焦距fl，右摄像机有效焦距fr，两摄像机之间的位置关系为：

(3)

其中M=[RT],

R和T分别为左摄像机坐标系(世界坐标系)与右摄像机坐标系之间的旋转矩阵和原点之间的平移向量。此时，在传感器坐标系下表示的空间被测点与两摄像机像面点之间的对应变换关系分别为：

(4)

(5)

由此，空间点三维坐标可以表示为：

(6)

(7)

(8)

(9)

(10)

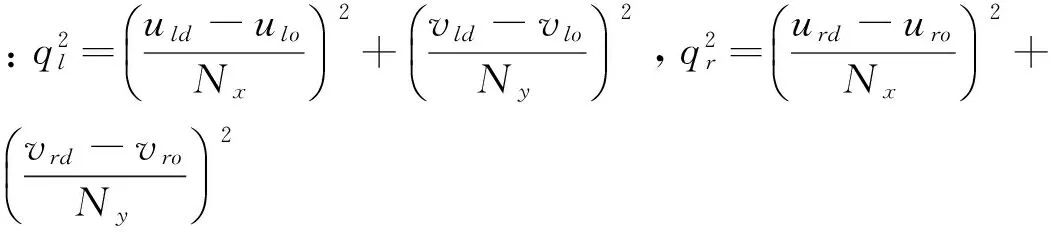
式(6)～(10)便是基于三角法的双目立体视觉模型的数学描述。如果旋转矩阵R和平移矩阵T已知，通过两摄像机像面点像素坐标(uldl,vld)和(urd,vrd)即可求解空间点的三维坐标(x,y,z)。

2.2基于射线交汇法的双目模型

图4所示为基于射线交汇法的简单双目模型，设世界坐标系为OXYZ，左摄像机图像坐标系为OlUlVl，右摄像机图像坐标系为OrUrVr，假定空间任意点P的世界坐标为(Xw,Yw,Zw)，点P在两台摄像机的成像平面上的像点分别为P1与P2，P1和P2的像素坐标分别为：(U1,V1)和(U2,V2)，两摄像机的投影矩阵分别为：

(11)

(12)

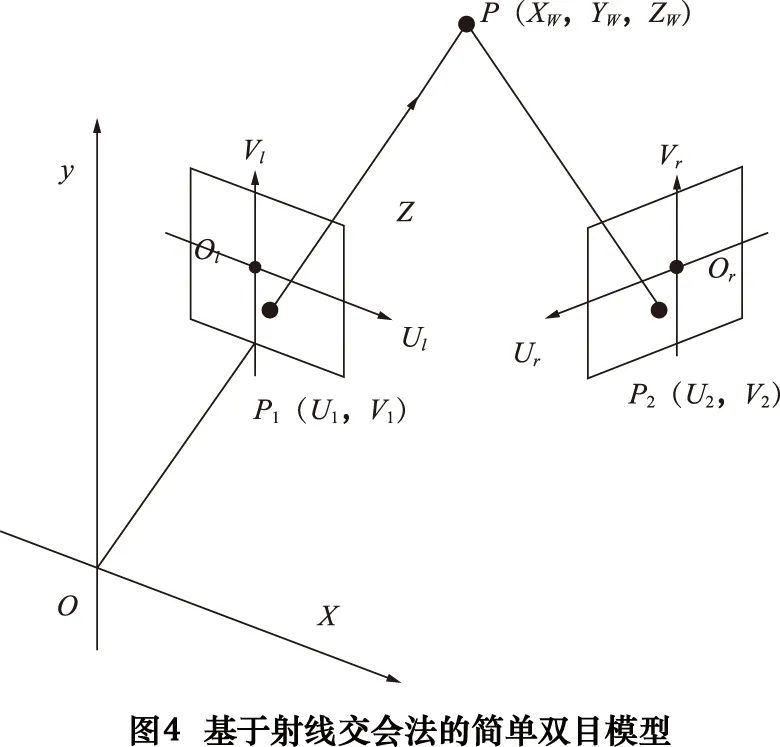
根据摄像机的成像模型有摄像机坐标系与世界坐标系之间的转换关系可表示为：

(13)

(14)

其中：zf1和zf2分别为空间点P在两台相机的光心坐标系中沿光轴方向的坐标值，M1=A1R1T1,M2=A2R2T2；A1、A2分别为左右摄像机的内参矩阵，R1、T1分别为左摄像机坐标系相对于世界坐标系的旋转矩阵和相对于原点之间的平移向量,R2、T2分别为右摄像机坐标系相对于世界坐标系的旋转矩阵和相对于原点之间的平移向量。

设左摄像机坐标系与世界坐标系重合，则此时：

(15)

M2=

(16)

由此得：

(17)

(18)

展开整理得到：

-flxx+(u1-uol)z=0

(19)

-flyy+(v1-vol)z=0

(20)

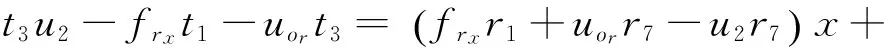
(21)

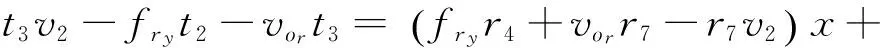
(22)

对于等式(19)-(22)，为方便计算用矩阵形式表示如下：

Kq=l

(23)

K=

(24)

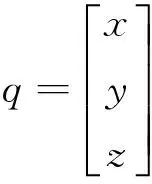
(25)

(26)

由于K不是方阵，为方便计算先求KTK,进而求得：

q=(KTK)-1KTl

(27)

(28)

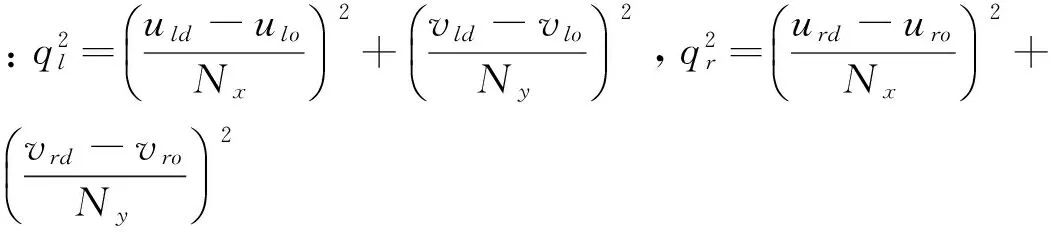
上述讨论表明：只要知道两台摄像机的内参矩阵和两台摄像机间的旋转、平移矩阵，便可由空间一点分别在两台像机像平面上的坐标求出空间点的三维坐标。

2.3特征点提取和匹配

为了精确提取空间中点在两像机像平面的坐标对，首先使用Harris算法提取图像中的点作为特征点。其原理如下：

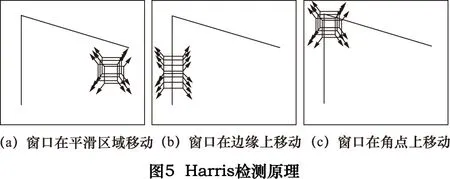
设定一个特定大小的窗口，让此窗口在图像上移动，以便图像灰度变化进行检测。图5a为窗口在平滑区域移动时的情况，可见窗口周边各方向的灰度没有变化。图5b为窗口在边缘上移动时的情况，可见窗周边各方向的灰度也没有变化。图5c为窗口在角点处移动的情况，可见窗口周边各个方向的灰度有明显变化。Harris算法正是利用了这个直观的物理现象，通过窗口周边各个方向上的灰度变化程度，来检测角点。

特征点提取完成之后，需要对两幅图像上提取到的特征点进行匹配。匹配时需要先进行粗匹配，利用特征点附近的特征信息，参考图像和待匹配图像有相似尺度和灰度信息，以参考图像作为模板在待匹配的图像上遍历，计算每个位置参考图像和待匹配图像对应位置的互相关度，建立一个局部匹配的准则，将Harris算法检测结果(两个特征点集合)，划分为多个一对一匹配对。

粗匹配之后，需要根据Ran sac算法[1]对粗匹配中的错误匹配点对进行剔除。Ran sac算法根据一组包含异常数据的样本数据集，计算出数据的数学模型参数得到有效样本数据。其基本假设是样本中包含正确数据(Inliers，可以被模型描述的数据)，也包含异常数据(Outliers，偏离正常范围很远、无法适应数学模型的数据)。异常数据可能是由于错误的测量、错误的假设、错误的计算等产生。同时Ran sac算法也假设，给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法。精匹配中使用的Ran sac算法基本思想描述如下：

(1)考虑一个最小抽样集的势为n的模型(n为初始化模型参数所需的最小样本数)和一个样本集P，集合P的样本数>n，从P中随机抽取包含n个样本的P的子集S初始化模型M。

(2)Sc=P/S中与模型M的误差小于某一设定阈值t的样本集以及S构成S*。认为S*是内点(Inliers)集，它们构成S的一致集(Consensus set)。

(3)若S*≥N，认为得到正确的模型参数，并利用集S*采用最小二乘法等方法重新计算新的模型M*；重新随机抽取新的S，重复以上过程。

(4)在完成一定的抽样次数后，若找到的抽样结果为一致集，则算法失败，否则选取抽样后得到的最大一致集判断内外点，算法结束。

2.4模型误差比对

通过将两种模型进行对比可发现，基于三角法的测量模型没有考虑到镜头畸变的问题，而基于射线交汇法的测量模型由于是从最原始的像机模型出发，考虑到了像平面中心的变化，通过将提取到的左右像机像平面坐标与标定出的左右像平面中心进行做差运算，之后再代入像机模型，从而消除了镜头畸变的影响。因此，基于射线交汇法的测量模型比基于三角法的测量模型有更好的精度。两者之间的误差计算方法如下：

文献[11]中将畸变分为x方向上畸变和y方向上畸变，两种畸变都分别由径向畸变、偏心畸变和薄棱镜畸变3种畸变组成。在正常情况下，径向畸变已经足以描述模型中的畸变，因此只考虑径向畸变即可。对于径向畸变描述如下：

(29)

(30)

(31)

由此得系统误差为：

(32)

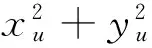
(33)

2.5实验与效果比对

实验中采用两台型号参数一致的高分辨率低畸变CCD摄像机进行实验，分别按照图3、图4的方法进行了实验，每次实验中分别使用左、右摄像机各拍摄一幅图像，再变换标定板的摆放方式，继续在左右拍摄点拍摄以得到左右图像，依此类推。实验采用左、右各12幅图像来标定，图像大小为1280×1024，标定重投影误差为0.6像素。双目系统标定所得内外参如下：

左右像机内参为：

左右像机畸变系数为：

两像机间的外参为：

对左右摄像机分别进行单目标定，在得到像机内参之后，再进行立体标定从而得到两像机间的旋转平移矩阵，然后进行立体匹配以获取某些对应的匹配点。如图6所示，分别将得到的高精度标定板上的多组匹配点对代入前文介绍的两种模型，从而测量这些点对间的距离。特征点提取和匹配效果如图7所示，得到的实验数据如表1所示。

3　结语

(1)在标定精度、提取精度、匹配精度、测量距离、像机主轴与Z轴夹角、基线长度、外界光线影响等影响因素都相同的情况下，基于射线交汇法的双目模型比基于三角法的双目模型有更高的测量精度。

(2)由实验数据可知，在摄像机标定和立体匹配后，根据提出的简单的双目模型算法，对高精度标定板上两点间的距离进行测量，测量误差都是小于1.5%，可见该算法还是能达到一定的精度。

表1各模型代入相同标定参数后对同一标准件测量结果比较

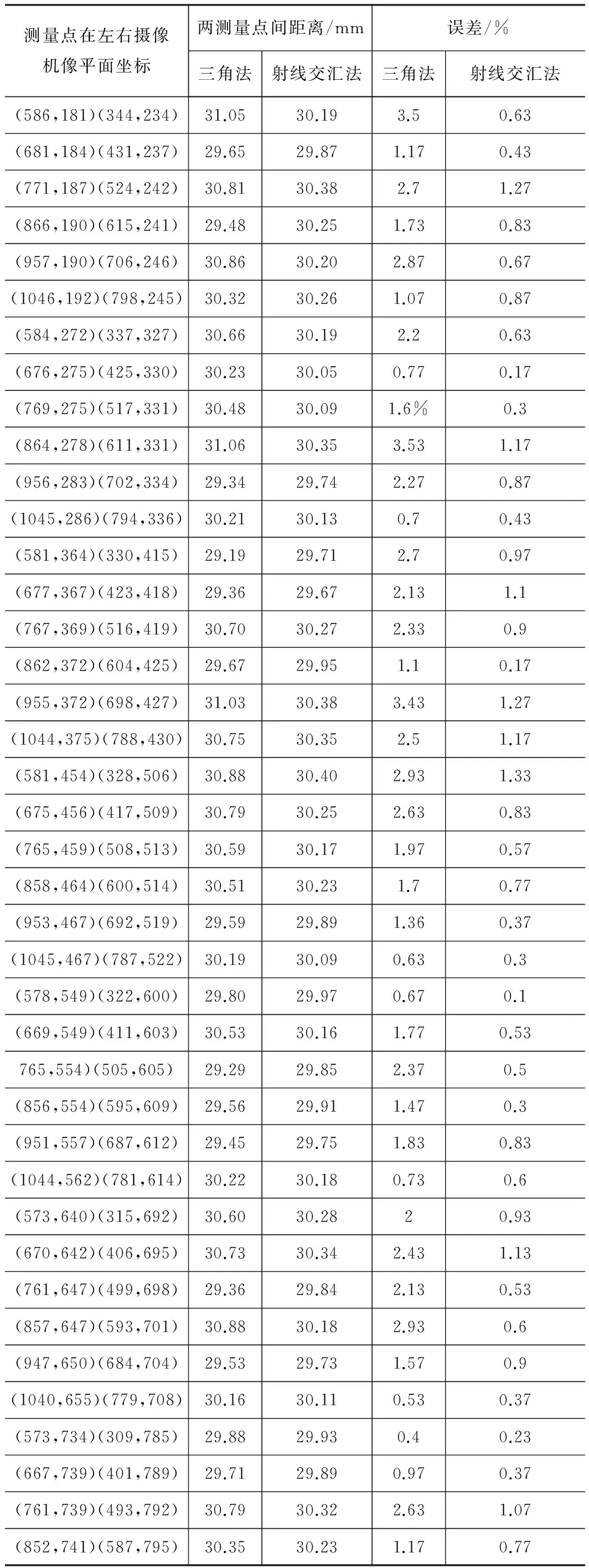
测量点在左右摄像机像平面坐标两测量点间距离/mm误差/%三角法射线交汇法三角法射线交汇法(586,181)(344,234)31.0530.193.50.63(681,184)(431,237)29.6529.871.170.43(771,187)(524,242)30.8130.382.71.27(866,190)(615,241)29.4830.251.730.83(957,190)(706,246)30.8630.202.870.67(1046,192)(798,245)30.3230.261.070.87(584,272)(337,327)30.6630.192.20.63(676,275)(425,330)30.2330.050.770.17(769,275)(517,331)30.4830.091.6%0.3(864,278)(611,331)31.0630.353.531.17(956,283)(702,334)29.3429.742.270.87(1045,286)(794,336)30.2130.130.70.43(581,364)(330,415)29.1929.712.70.97(677,367)(423,418)29.3629.672.131.1(767,369)(516,419)30.7030.272.330.9(862,372)(604,425)29.6729.951.10.17(955,372)(698,427)31.0330.383.431.27(1044,375)(788,430)30.7530.352.51.17(581,454)(328,506)30.8830.402.931.33(675,456)(417,509)30.7930.252.630.83(765,459)(508,513)30.5930.171.970.57(858,464)(600,514)30.5130.231.70.77(953,467)(692,519)29.5929.891.360.37(1045,467)(787,522)30.1930.090.630.3(578,549)(322,600)29.8029.970.670.1(669,549)(411,603)30.5330.161.770.53765,554)(505,605)29.2929.852.370.5(856,554)(595,609)29.5629.911.470.3(951,557)(687,612)29.4529.751.830.83(1044,562)(781,614)30.2230.180.730.6(573,640)(315,692)30.6030.2820.93(670,642)(406,695)30.7330.342.431.13(761,647)(499,698)29.3629.842.130.53(857,647)(593,701)30.8830.182.930.6(947,650)(684,704)29.5329.731.570.9(1040,655)(779,708)30.1630.110.530.37(573,734)(309,785)29.8829.930.40.23(667,739)(401,789)29.7129.890.970.37(761,739)(493,792)30.7930.322.631.07(852,741)(587,795)30.3530.231.170.77

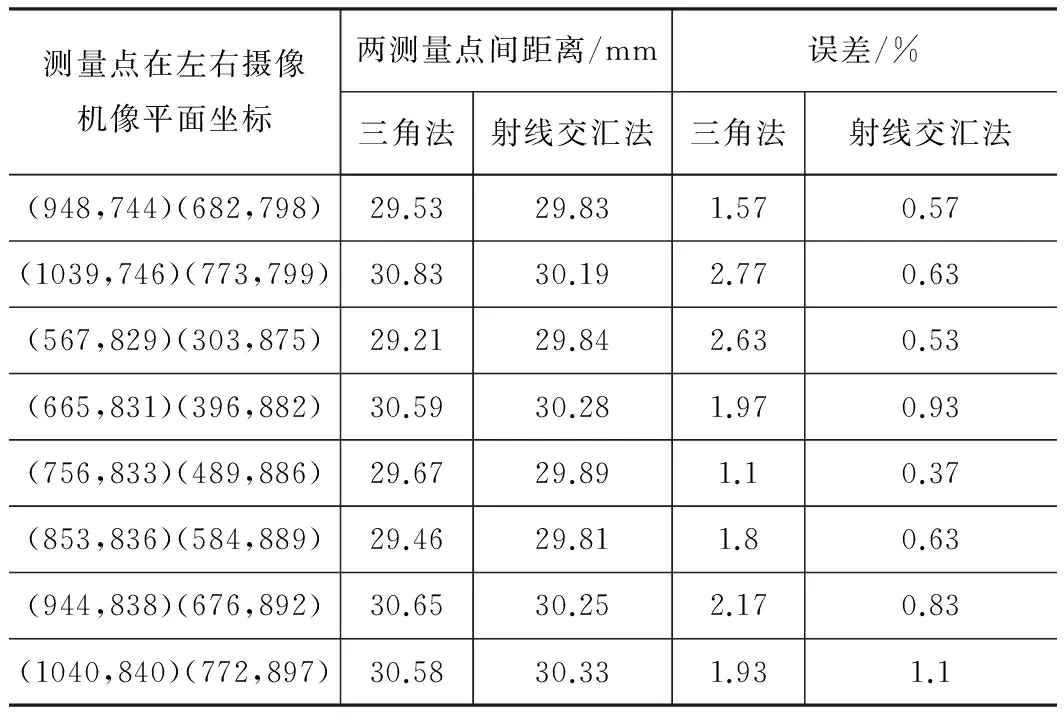
测量点在左右摄像机像平面坐标两测量点间距离/mm误差/%三角法射线交汇法三角法射线交汇法(948,744)(682,798)29.5329.831.570.57(1039,746)(773,799)30.8330.192.770.63(567,829)(303,875)29.2129.842.630.53(665,831)(396,882)30.5930.281.970.93(756,833)(489,886)29.6729.891.10.37(853,836)(584,889)29.4629.811.80.63(944,838)(676,892)30.6530.252.170.83(1040,840)(772,897)30.5830.331.931.1

(3)由于标定误差、人为误差、特征点提取误差及其他因素的影响，如立体匹配时互相关匹配只查找两幅图像之间的强匹配点(即强纹理)，Ran sac算法也只是剔除错误的匹配点，并没有检测到漏匹配点对等，这些因素都导致了两点间距离的测量精度有一定的波动。

(4)基于射线交汇法的双目模型相比于基于三角法的双目模型考虑到了左、右像机像平面中心的变化带来的影响，通过将提取到的左右像机像平面坐标与标定出的左右像平面中心进行做差运算，消除了镜头畸变的影响。因此，基于射线交汇法的测量模型比基于三角法的测量模型有更好的精度。

[1]章毓晋.图像理解与计算机视觉[M].北京：清华大学出版社，2011.

[2]Bouguet J Y. Camera calibration toolbox for matlab[DB/OL].http://www.vision.caltech.edu/bouguetj/calib_doc/index.html.2013.

[3]Song X, Yang L，Liu Z. An improved two view convergent-style-based disparity estimation algorithm [C]. International Conference on Audio, Language and Image Processing, 2012:698-704.

[4]单洁，唐篧，姜晖.双目立体相机中实时匹配算法的FPGA实现[J].激光与红外, 2013, 43(12):1406-1410.

[5]NingKelin, Zhang Xiaoying, Ming Yue. Stereo matching algorithms with different cost aggregation[J].Proceedings of International Conference on Computer Science and Information Technology,2014(1):647-653

[6]Lorenzo Solrgi. Two-view geometry estimation using the Rodrigues rotation formula[C]. 18th IEEE International Conference on Image Processing (ICIP),2011:1009 - 1012.

[7]Rhemann C, Hosni A, Bleyer M, et al.Fast cost-volume filtering for visual correspondence and beyond [C].In Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on IEEE，2011：3017-3024.

[8]Chen D, Ardabilian M, Chen L.A novel trilateral filter based adaptive support weight method for stereo matching[J].BMVC，2013:318.

[9]Psota E T, Kowalczuk J, Carlson J, et al. A local iterative refinement method for adaptive support-weight stereo matching [C].International Conference on Image Processing, Computer Vision, and Pattern Recognition,2011:271-277.

[10]Zhang K, Li J, Li Y, et al.Binary stereo matching[C].In Pattern Recognition (ICPR), 2012 21st International Conference on IEEE,2012:356-359.

[11]邾继贵.视觉测量原理与方法[M].北京：机械工业出版社,2012.

[12]刘瑜.刘缠牢.苏海.一种基于结构光双目视觉的特征匹配算法研究[J].光学仪器,2014,36(2):161-166.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

A measurement methodbased on the binocular stereo vision theory

YU Zhen, LIU Shugui

(State Key Laboratory of Precision Measuring Technology&Instrument, Tianjin University, Tianjin 300072, CHN)

A binocular method on account of ray intersection models is proposed based on the binocular stereo vision theory. After the binocular system is calibrated, using the Harris algorithm to extract the feature points of the images. Then the three-dimensional coordinates of the feature points in the camera coordinate system is obtained after stereo matching in order to calculate the distances between any points. And it is provided to be more accurate than another results which are calculated by the other binocular model. Experimental results show that this method can achieve more accurate three-dimensional measurement of objects.

ray intersection method; binocular model;three-dimensional measurement

TP391.41

B

10.19287/j.cnki.1005-2402.2016.08.028

(编辑李静)(2016-06-21)

160839

* 天津自然科学基金重点项目(13JCZDJC34500)