高精度球体加工机床加压系统的研究*

余龙芬　袁巨龙　周芬芬　赵　萍　张传通

(浙江工业大学机械工程学院，浙江 杭州 310014)



高精度球体加工机床加压系统的研究*

余龙芬袁巨龙周芬芬赵萍张传通

(浙江工业大学机械工程学院，浙江 杭州 310014)

为解决传统高精度球体加工机床无法实现加工载荷精确控制的问题，提出了一种新型机械加压系统，并通过优化结构设计，确定合理的参数，使加压系统从原有的加压精度12%F·S提升到0.67%F·S，满足系统所需的加压精度2.6%F·S。

加工载荷；加压系统；加压精度

高精度球体是高精度轴承的关键零件之一，广泛应用于精密机床设备和检测设备中[1-2]。高精度球体加工机床用于球体精研、超精研以及抛光等工序；机床精度对最终成球质量有着至关重要的作用[3]。洛阳轴承研究所的郭静芬[4]结合大量的生产实验，总结了加工过程中加工机床各参数对最终成球质量的影响，具体因素的影响程度如表1所示。

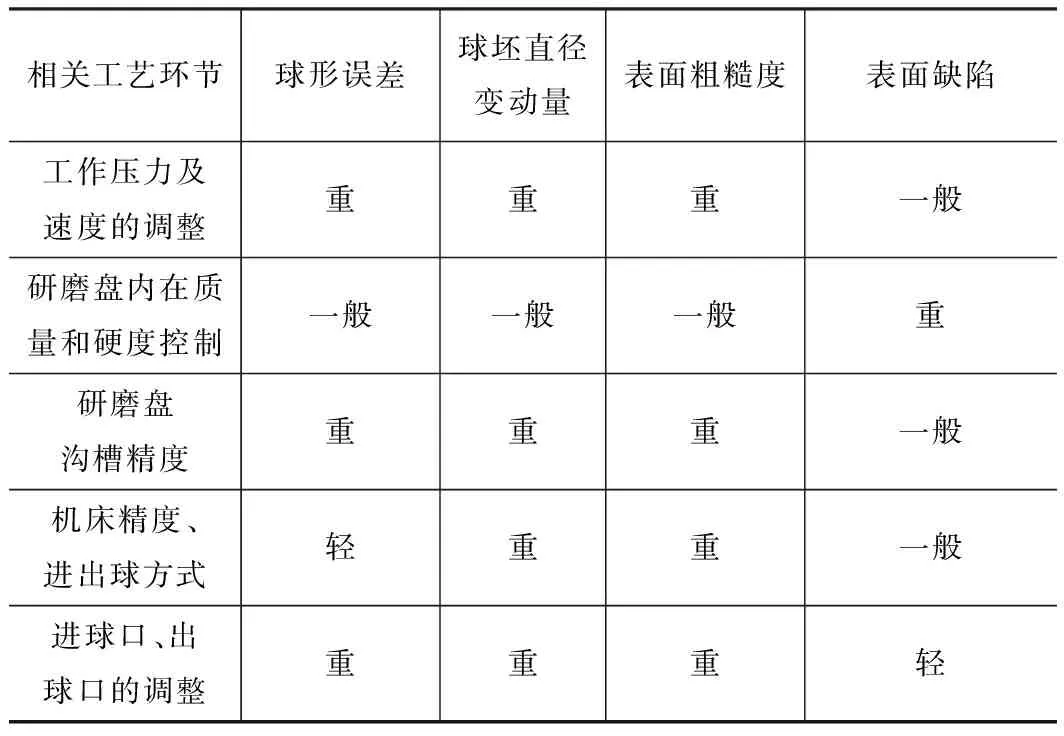
表1　加工机床对成球质量的影响程度

从表1中可以看出，球体加工的最终质量受到众多工艺参数的影响，其中加工载荷(工作压力)是最主要的工艺参数之一，因此做到加工过程中加工载荷的精确可控，对生产高精度球体有着重大意义[5-7]。所以本文针对传统V型槽机床的加压系统进行分析研究。

1　传统V型槽式机床加压系统所需加压精度

所谓加压系统所需的加压精度，即球体加工机床的最小压力分辨率与加压系统加压范围之比，其单位为%F·S, 即满量程百分比。球体加工机床所需的最小压力分辨率即为单球最小压力与球体总数之积。单球的最小压力可以等效为球体加工过程中能够确保球体做无打滑研磨运动的最小压力[8]。

对于磨盘直径为800mm的传统V型槽式加工机床，加工对象为直径10mm氮化硅陶瓷球，经过实验测量计算，单球的最小压力0.13N。根据机床所需最小压力分辨率定义，计算得机床所需的加压精度为2.6%F·S(加压系统加压范围为0～15kN)。

2　新型加压系统

2.1加压系统组成

所提出的新型机械加压系统的主要结构如图1所示：

2.2加压系统加压性能测试

测量磨盘直径为800mm的传统V型槽式加工机床所需的加压精度，以上磨盘自重4 000N为分界点，两边各取8～10个点(加压系统加压范围为0～15kN)，计算所取加压点的实际加压误差，实际测量结果如图2示。从图2可以看出：在量程范围内，其最大加压误差为1 800N，加压精度为12%F·S，无法满足加压精度2.6%F·S的要求。

3　加压系统的改进

3.1机床上磨盘重心计算及调平

V型槽式球体加工机床，其上磨盘(图3所示)具有一个入料口，使上磨盘重心位置偏离其几何中心，而设计方案中丝杆装配位置并未精确测定偏心位置，影响了加压精度。因此需要计算V型槽式机床上磨盘的重心位置。

计算得上磨盘的重心坐标为(0，33.39)，即其重心位置为y轴方向上偏离其几何中心33.39mm，与上磨盘丝杆装配位置的偏心量62.5mm相差较大。

原有的加压系统,弹簧组的调平作用已经无法修正偏移量所带来的误差，因此需要在适当位置上增加配重块以保持上磨盘的重力平衡来进行调平。配重块装配位置距离其原上磨盘丝杆装配位置300mm，根据重力矩平衡的原理，可以列出方程：

P配重(300+62.5-33.39)=P上磨盘(62.5-33.39)

(1)

其中P上磨盘为上磨盘的重量，为4 108N，根据公式(1)可得P配重=363.43N， 其质量为m配重=37.1kg。安装配重块后的上磨盘如图4所示。

3.2加压系统弹簧组计算优化及有限元分析

3.2.1弹簧组计算

对于V型槽式加工机床，考虑上磨盘自重，要求其上弹簧组最大工作载荷12kN，工作行程25mm，下弹簧组最大工作载荷6kN，工作行程15mm。要求所有弹簧组变载荷循环次数达到10 000次，并且考虑到弹簧组的弹簧数量影响着加压系统的加压均匀性，弹簧组弹簧参数如表2所示。

3.2.2结构静力学分析

针对所设计的3组加压弹簧，设置5个对比实验组，对加压系统在弹簧组最大工作载荷下的加压均匀性进行了有限元分析，实验条件列于表3。

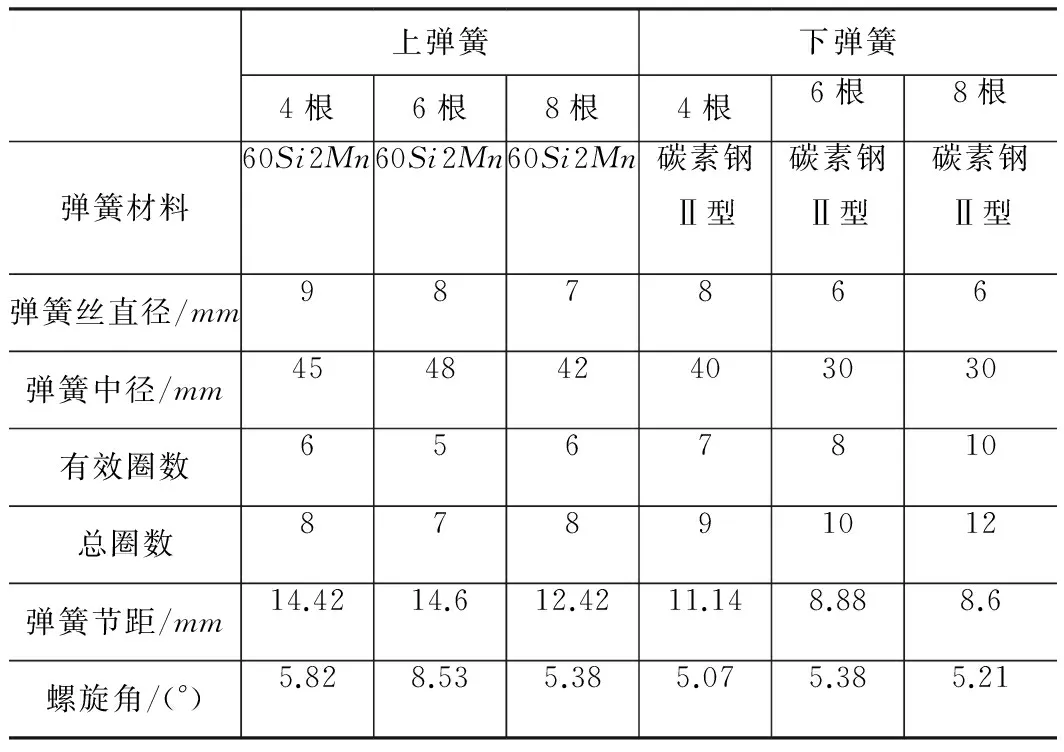
表2　传统V型槽式球体加工机床上、下弹簧组单根弹簧参数

表3　仿真对比组实验条件

基于有限元分析软件ANSYS，对弹簧组建立模型，加工球坯作为加压系统的最终受力物体，起到支撑作用，将球坯简化为一块内径450mm，外径770mm，高10mm的圆环体，加压系统采用的材料特性如表4所示。

表4　实体单元材料特性

网格划分后的模型如图5所示，施加载荷以及约束后的模型如图6所示。

加压系统的总体变形图如图7所示，工件表面所受的应力如图8所示。

根据仿真所得的工件受力云图，可以得到以下结论：

(1)对比图8中的a、b、c，在相同的安装直径条件下，工件的表面应力分布情况较为相近，只是所受应力的极值有所差异。在4根弹簧情况下应力最大，6根弹簧情况下应力最小，两者相差不超过3.6%，几乎可以忽略。这是由于弹簧在圆周均匀分布，在相同压力条件下，向工件施加的压力也近似相等。

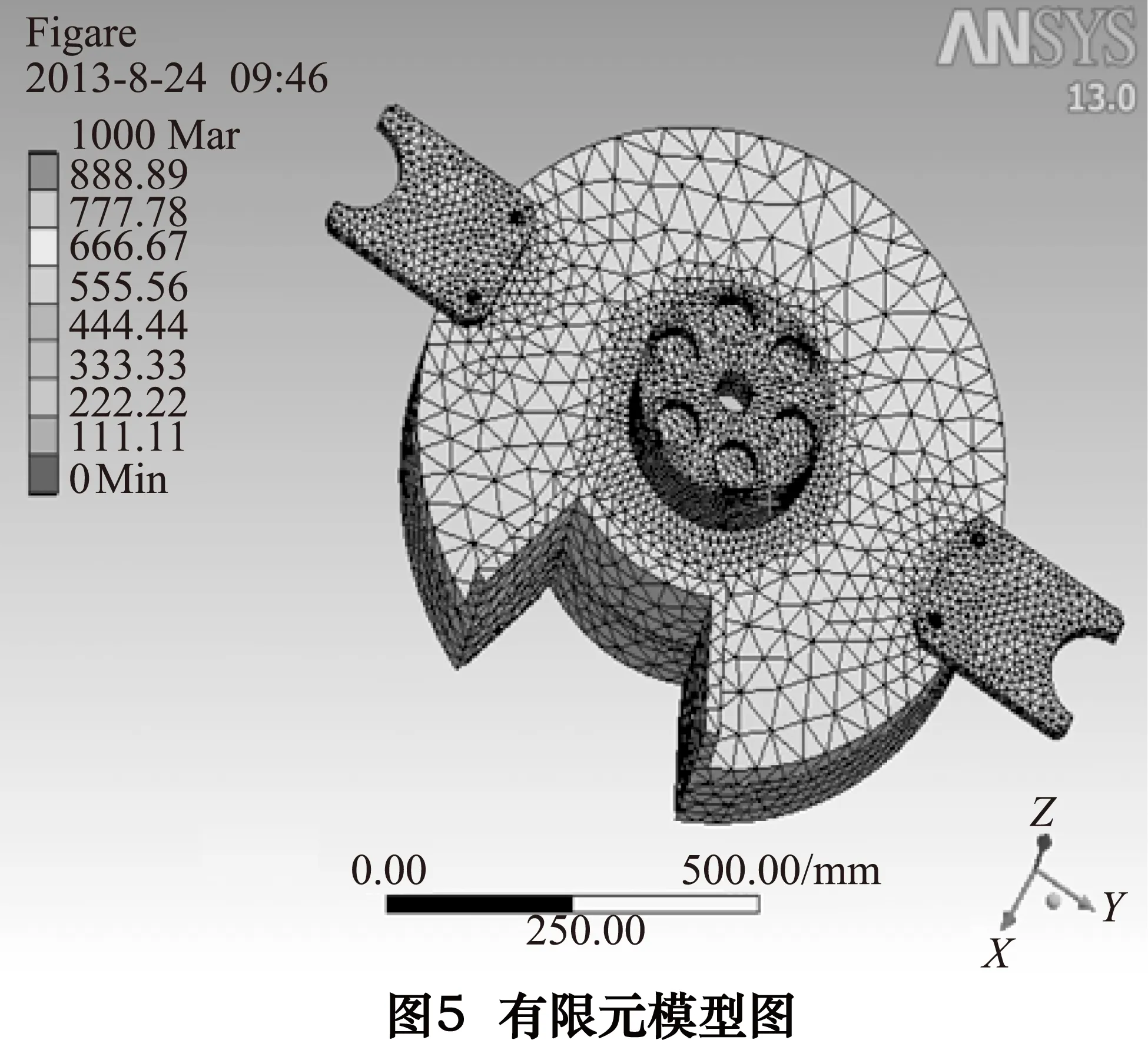
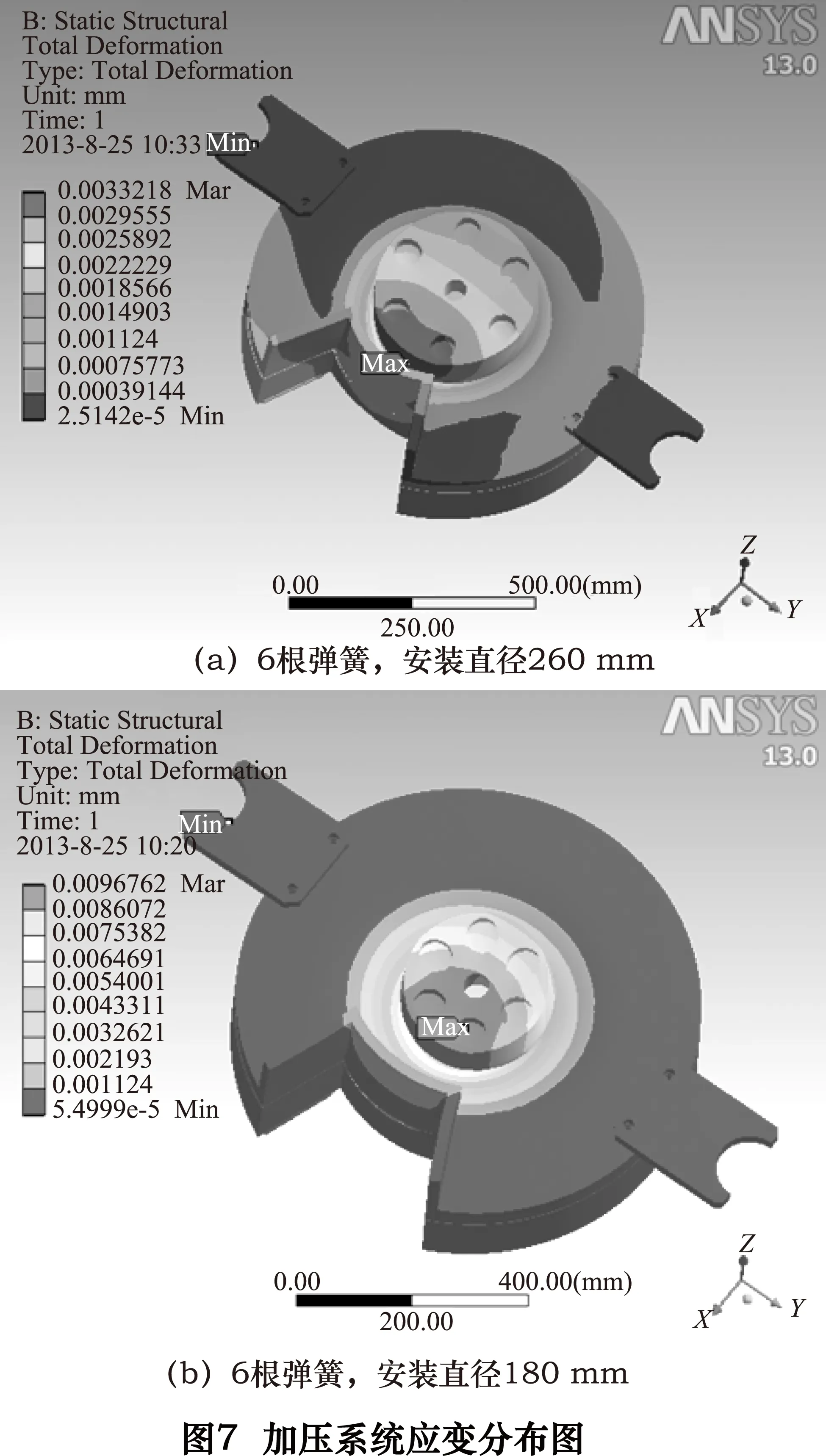
(2)对比图8中c、d、e，可以看到在相同的弹簧个数的条件下，工件表面应力分布的均匀性受弹簧组安装直径的影响较大。随着弹簧组安装直径减小，工件表面的应力分布越均匀。在所受应力极值上来看，弹簧组安装直径越小，其所受的应力极值越大，但其应力极值相差不超过3.5%，亦可忽略不计。从加压系统的总体变形图(图7所示)可以看到，弹簧组安装直径越大，加压系统整体的变形也越大。这是由于上磨盘入料口处去除了大量材料，使系统加压时，加压点离加料口越近，造成的变形越大，从而引起了工件更大的应力变化。

3.2.3弹簧组动力学分析

采用机械动力学分析软件ADAMS，为减少仿真的计算量，对加压系统模型进行简化：

(1)将工件简化为均布于圆周上的，共8颗直径为10mm的球坯。

(2)将球体的振动信号的幅值转化为球体圆度误差引起的振动，即球坯为椭球，长轴比短轴长0.043mm；在研磨盘转速为15r/min的条件下，球坯自转角速度根据ADAMS单位制转化为外沟道角速度2 340°/s，内沟道角速度1 470°/s。

加压系统的材料特性如表4所示，加载完的模型如图9所示。根据加压系统动力学分析模型，将接触力结果分为两组讨论：①相同弹簧个数下球坯接触力的变化比较，结果如图10所示；②相同安装直径下接触力的变化比较，结果如图11所示。图中，0.5s之前波形的波动是球从启动到达到标定速度对上磨盘的冲击造成的，因此主要对0.5s以后的波动图像进行对比。

根据图10与图11，可以得出以下结论：

(1)在具有相同弹簧个数的情况下，根据图10可以看出，不同的安装直径对球体接触力的波动影响不大。这是由于不同安装直径对加压系统的主要影响表现为对上磨盘变形的影响，而根据静力学仿真的结果(如图7所示)，其变形量的极大值也小于0.01mm，这些变形量对于弹簧组而言产生的变形力较小，因此在具有相同弹簧刚度以及弹簧阻尼系数的条件下，安装直径对于球坯表面的接触力影响也并不明显。

(2)在弹簧组具有相同安装直径的条件下，由图11可以看出，在4根弹簧的条件下，出现了几个接触力的剧烈波动；对比6根弹簧与8根弹簧的接触力，发现两者的接触力波动差别并不明显。因此对于加压系统而言，考虑加工成本的情况下，6根弹簧为最优弹簧个数。

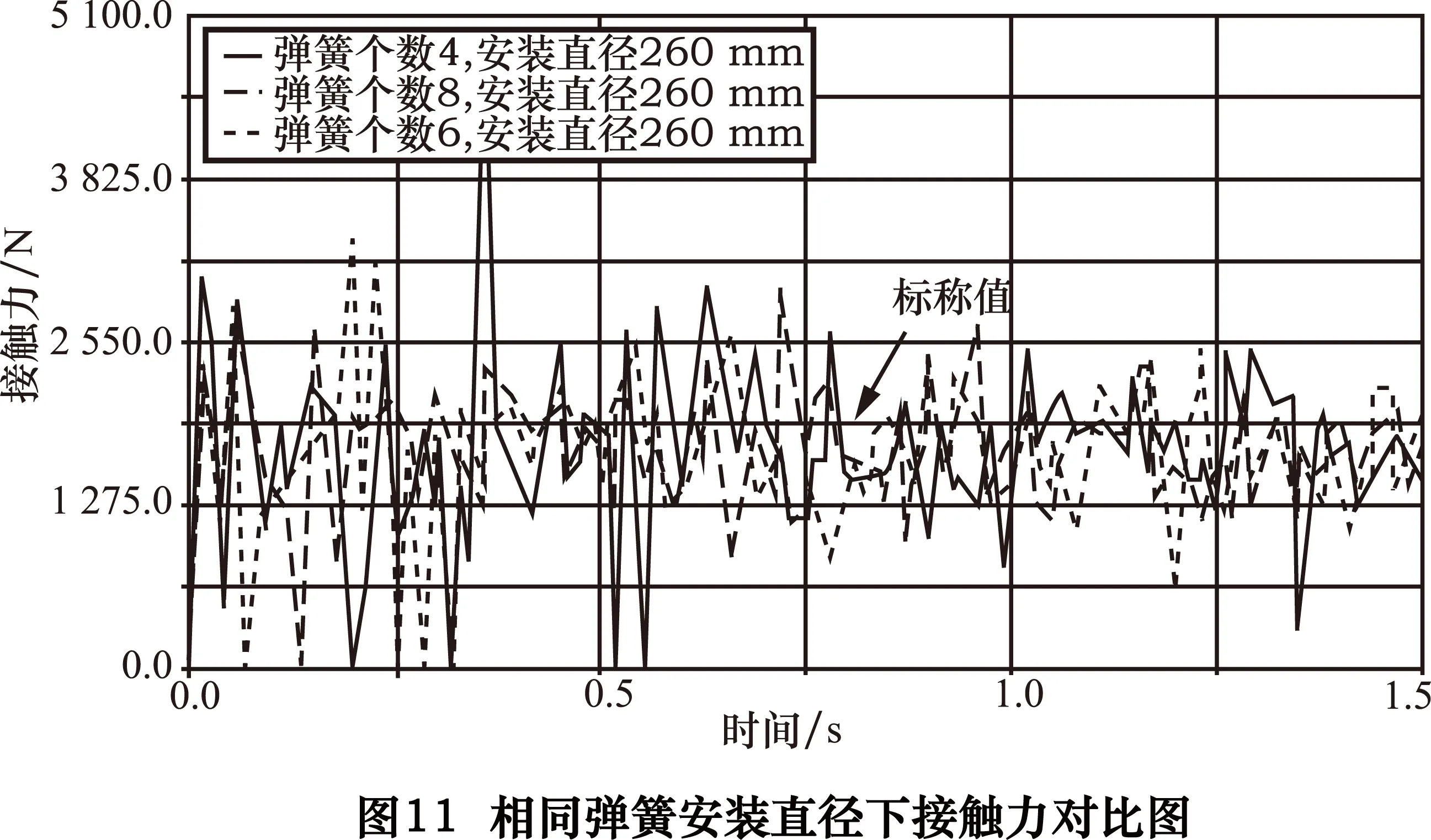
综上所述，弹簧安装直径越小，所加工的工件受力越均匀；而弹簧组的弹簧个数是影响球体振动下球体与上研磨盘之间接触力的主要因素，6根弹簧属于最优解。在综合考虑静力学与动力学分析的情况下，安装直径180mm，弹簧个数6为最优的设计组。

4　改进后加压系统精度测量

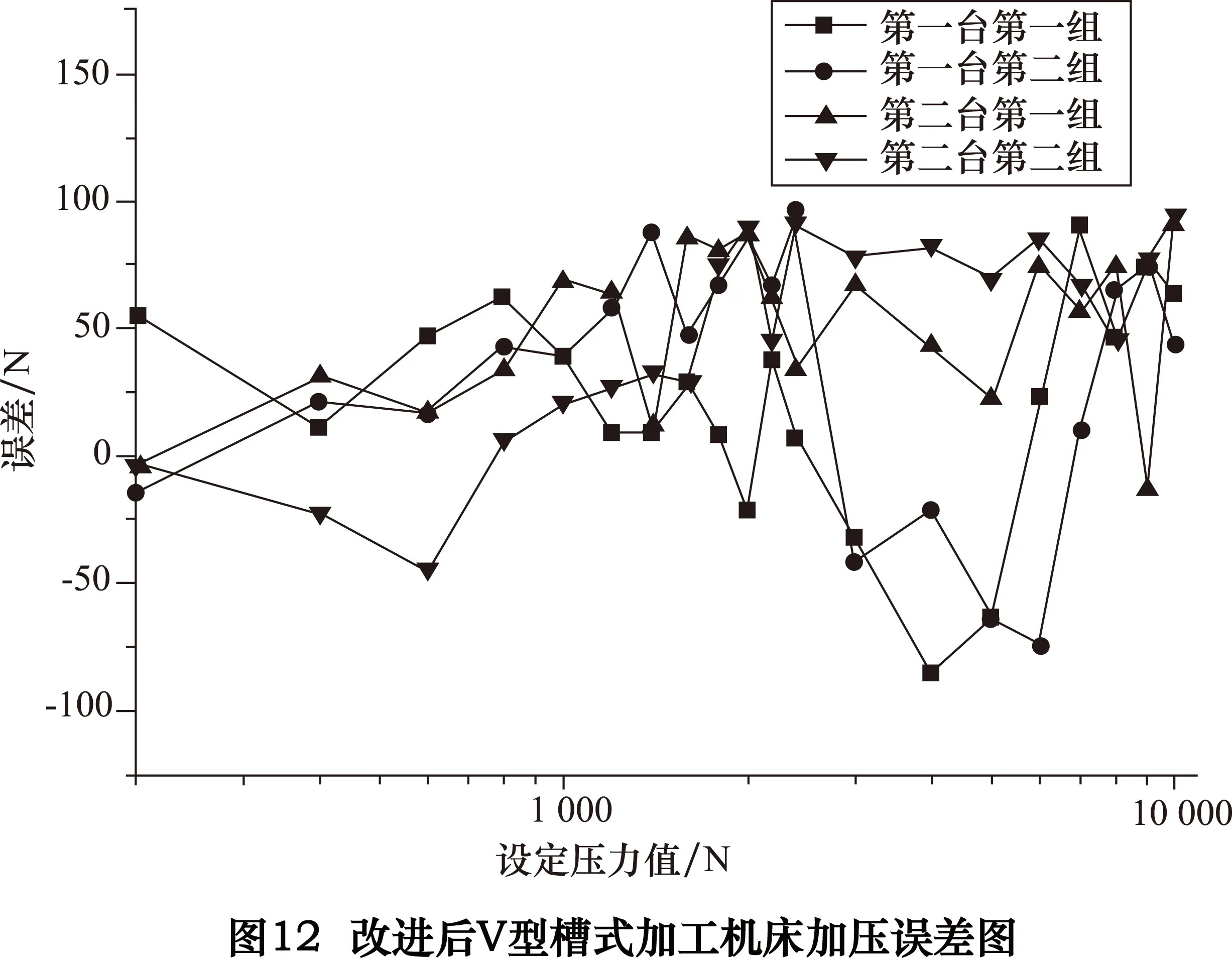
改进后的加压误差结果如图12所示。

从图中可以看到加工机床的加压误差在±100N内，重复误差小于100N，并且其加压误差呈现随机分布，加压稳定性良好。就加压误差的精度而言，已经达到了0.67%F·S，满足了2.6%F·S的精度要求。

5　结语

本文主要对加压系统进行了两个方面的改进：

(1)针对现有的传统V型槽式机床加压系统上磨盘未调平的问题，对加压系统的上磨盘重心位置进行了精确计算，并根据计算结果，对现有的上磨盘采用配重块的形式进行调平处理。

(2)对加压系统的弹簧组进行优化设计，并对设计结果进行静力学和动力学仿真分析，根据分析结果，在6根弹簧，安装直径180mm的情况下加压系统的加压均匀性最好。在对加压系统进行相应改进后，加压系统的加压误差精度达到了0.67%F·S，能够满足系统所需的2.6%F·S的精度要求。

[1]陈力, 冯坚. 氮化硅陶瓷材料的研究现状及其应用[J]. 硬质合金, 2002, 19(4): 226-229.

[2]WangLQ,SnidleRW,GuL.Rollingcontactsiliconnitridebearingtechnology:areviewofrecentresearch[J].Wear, 2000,246(1): 159-173.

[3]张永乾, 吴朝阳. 我国钢球加工工艺设备的现状及发展趋势[J]. 轴承, 2011(4): 59-62.

[4]郭静芬.G3钢球批量制造工艺实施要点分析[J]. 轴承, 2003(3): 20-23.

[5]KangJ,HadfieldM,TobeS.ResidualstressfieldofHIPedsiliconnitriderollingelements[J].CeramicsInternational, 2002, 28: 645-650.

[6]RenCZ,WangTY,JinXM,etal.Experimentalresearchontheresidualstressinthesurfaceofsiliconnitrideceramicballs[J].JournalofMaterialsProcessTechnology,2002(129): 446-450.

[7]StolarskiTA,TobeS.Theeffectofacceleratedmaterialremovalonroundnessandresidualstressesinceramicballs[J].Wear, 1997, 205(S1-2): 206-213.

[8]吕冰海. 陶瓷球双转盘研磨方式及成球机理的研究[D]. 哈尔滨：哈尔滨工业大学, 2007: 18-23.

(编辑孙德茂)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Studyontheloadingsystemofprecisionballprocessingmachinetool

YULongfen,YUANJulong,ZHOUFenfen,ZHAOPing,ZHANGChuantong

(SchoolofMechanicalEngineering,ZhejiangUniversityofTechnology,Hangzhou310014，CHN)

Toovercomelimitationsthatintraditionalprecisionballprocessingmachinetool’sloadingsystem,processingloadcannotbeaccuratelycontrolled,soanewmechanicalloadingsystemisdevelopedinthispaper.Andoptimizingthestructureoftheloadingsystemtomakeitsoriginalloadingprecision12%F·Sincreaseto0.67%F·S,meetingtherequiredloadingprecision2.6%F·S.

processingload;loadingsystem;loadingprecision

2015-08-05)

160208

*国家自然科学基金(51375455)