一种基础模糊理论的自适应数据平滑方法

胡昌林，王　蕾

(1. 南京电子技术研究所,　南京 210039；　2. 南京工程学院 自动化学院，　南京 211167)



·数据处理·

一种基础模糊理论的自适应数据平滑方法

胡昌林1，王蕾2

(1. 南京电子技术研究所,南京 210039；2. 南京工程学院 自动化学院，南京 211167)

针对情报雷达组网数据融合系统中目标融合航迹质量的优化方法进行研究，从人在融合系统中的作用出发，通过数据挖掘，寻找融合航迹质量优化途径，提出了基于模糊理论的自适应平滑方法，对移动平均法进行改进，得到二次平滑方法，并将模糊推理融入到其参数自适应调节。试验证明：该方法可很好地提高系统的融合航迹质量，为用户提供了高质量、高可靠性的融合态势数据。

数据融合；自适应平滑；模糊推理；自适应调节；移动平均；数据挖掘

0　引　言

情报雷达组网系统将区域内不同功能、不同体制、不同频段的多部雷达进行综合集成，实现区域内情报数据分级处理、逐层融合、综合分析，形成统一的战场态势，并进行辅助态势分析，评估威胁。在情报雷达组网系统中，通过对多传感器信息融合，获取融合信息，可以极大地提高战场侦察的作战效能。

多传感器信息融合系统作为情报组网系统的重要组成部分，受到用户的高度重视和广泛应用。其主要任务之一是将多个传感器提供的观测数据传送至数据融合处理中心，经情报综合或数据融合建立起高质量的、清晰的目标综合航迹报告。在该系统中，由于大量的探测信息被利用，大大提高了系统的可靠性。同时，由于不同传感器具有不同的探测性能，如：不同的传感器测量随机误差、测量系统误差等都不尽相同，由此导致融合航迹平滑度差。该问题可以通过两种途径解决：第一，对融合前的信息进行质量评估，评估结果用于指导信息融合策略，从而得到高质量的融合航迹；第二，采用反馈机制，对融合后的航迹进行自适应优化处理。本文采用第二种途径，将模糊理论用于优化参数的自适应调整，对融合后的航迹进行自适应优化处理，可提高融合信息的质量。

本文的内容安排如下：首先，对模糊理论和航迹平滑方法进行概述；其次，对基于模糊理论的自适应平滑方法进行设计；然后，采用仿真实验对该方法进行验证；最后，对该自适应方法进行小结。

1　理论基础

模糊理论[1]是基于“专家知识”，采用语言规则表示的一种人工智能策略，它有一套完整的基础理论与设计、综合方法。模糊语言、模糊逻辑系统、模糊推理是模糊理论的重要组成部分。模糊推理的基本思想，就是要用模糊集方法来模拟人的思维和推理过程。它属于一类不确定性推理技术，其基础是Zadeh[2]最早于1965年提出的模糊集合论。

信息融合是综合利用多个来源的信息，从中提取质量高于任何单一信息的综合信息的过程[3]。目前该领域已经产生了一些以不确定性理论为基础的技术，它们的代表是贝叶斯推理、证据推理和模糊推理[4]。这些技术各有特点，其中，模糊推理可以在概念的内涵和外延的边界不清或概念之间的关系残破的情况下进行逻辑推理，它有着简单有效的突出特点。因此，模糊推理已经在相当多的领域中得到了成功应用，如：人工智能、模糊控制、信息融合、军事决策[5-7]。

航迹平滑[8]可以最直接地提高信息融合的质量，引起了多方用户的重视。常用的平滑方法包括：因果分析法、简易平均法、移动平均法、趋势外推法等。这些平滑方法，从事物的原因和结果两个角度进行分析和综合，找到平滑的策略或方法。因果分析法和趋势外推法是基于对事物原因的分析进行平滑的方法；简易平均法和移动平均法是从事物发展的结果进行分析，找到提高平滑度的方法。

2　基于模糊理论的自适应平滑方法

在信息融合系统中，由于影响融合航迹质量的因素错综复杂，影响因素包括不同传感器的性能指标、多传感器之间的协同性能指标以及环境的因素等。因此，我们选择从结果出发对融合航迹进行平滑处理。对移动平均法进行改进，得到二次平滑方法，并将人工智能(模糊推理)融入到其参数调整中，来提高融合航迹的质量。

2.1二次平滑方法

简单移动平均平滑方法的各元素的权重都相等，其计算公式如下

(1)

式中:Sk-1为t时刻的平滑值；N为移动平均的采样周期个数；Zk-1是前一时刻的测量值；Zk-2、Zk-3、Zk-N分别为k-2、k-3直至k-N时刻的测量值。

则k时刻的平滑值为

(2)

由式(1)和式(2)可以得到递推形式的移动平均平滑公式

(3)

采用式(3)的递推形式，进行两次移动平均，并求加权平均，即可得到二次平滑方法。该方法的公式简单，也容易实现。它既保留了移动平均法的优点，又可减少数据的存贮量；同时，由于它能把各历史数据点充分修匀，能较为准确地反映数据点的变化趋势，因而得到较好的平滑效果。但是该方法在使用过程中存在一个明显不足，即平滑参数的选择无确定的方法，实际工作者只能凭借个人工作经验来选择。且平滑参数一旦确定，就不能依据时间序列的阶段性特点而变化。这样的平滑模型并不能较真实地、动态地反映时间序列。针对上述不足，本文设计了一种模糊自适应平滑模型。该模型实现了对时间序列数据的自适应动态平滑，具有工程实用性。

2.2基于模糊理论的自适应平滑方法

模糊自适应平滑系统的基本框图，如图1所示。对平滑误差均值和方差进行实时评估，根据评估结果，采用模糊推理方法，对平滑参数进行实时调整，达到减小平滑误差均值和方差的目的，从而提高融合信息的综合质量。

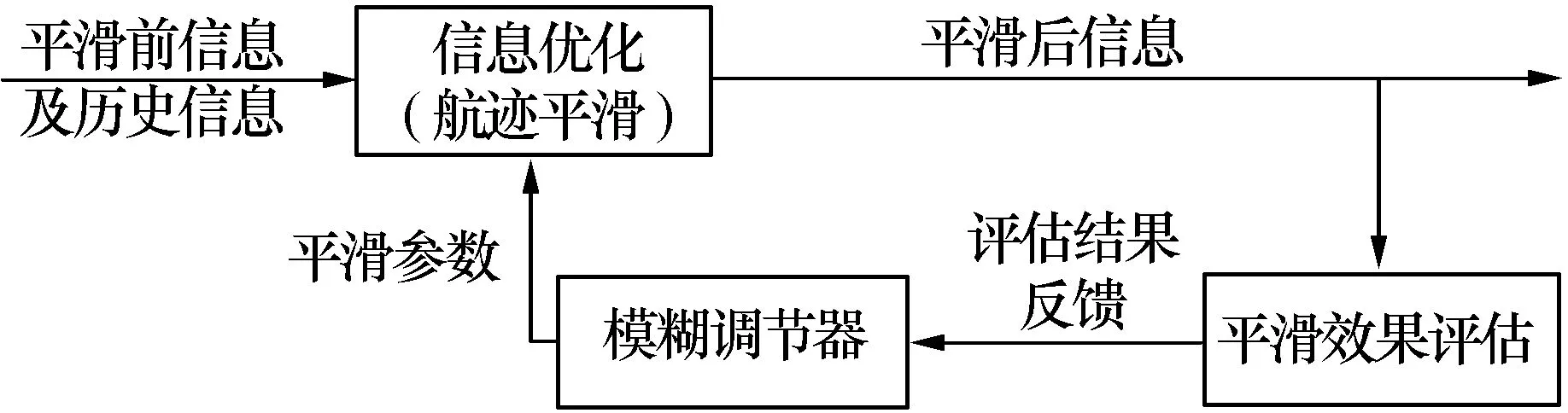
图1　模糊自适应平滑系统的基本框图

2.2.1选择模糊变量

分析多传感器信息融合系统时，对融合航迹的质量要求为：首先，使融合航迹尽量接近目标真实航迹，即要求融合航迹具有较高的精度；其次，使融合航迹尽量平滑，即要求融合航迹的抖动性较小，平滑性较高。因此，将融合航迹的误差均值Mx和误差方差Vx作为模糊规则的前项，而平滑参数的变化系数Cx作为模糊规则的后项。

常规模糊调节器[9]如图2所示。首先，将输入量转化为模糊量供模糊逻辑决策用；然后，模糊决策器根据控制规则决定的模糊关系R，应用模糊逻辑推理算法得出模糊输出；最后，经清晰化计算得到的调节值去调节被调参数。

图2　常规模糊化调节器

2.2.2模糊化

根据融合航迹Mx、Vx的均值和方差对其进行模糊化。将变量Mx、Vx向其方差的某一方向扩展可以得到该变量的一个论域，在这个论域上，按照与变量均值的距离建立模糊语言描述集合，采用三角形的隶属函数基本关系，如图3所示。

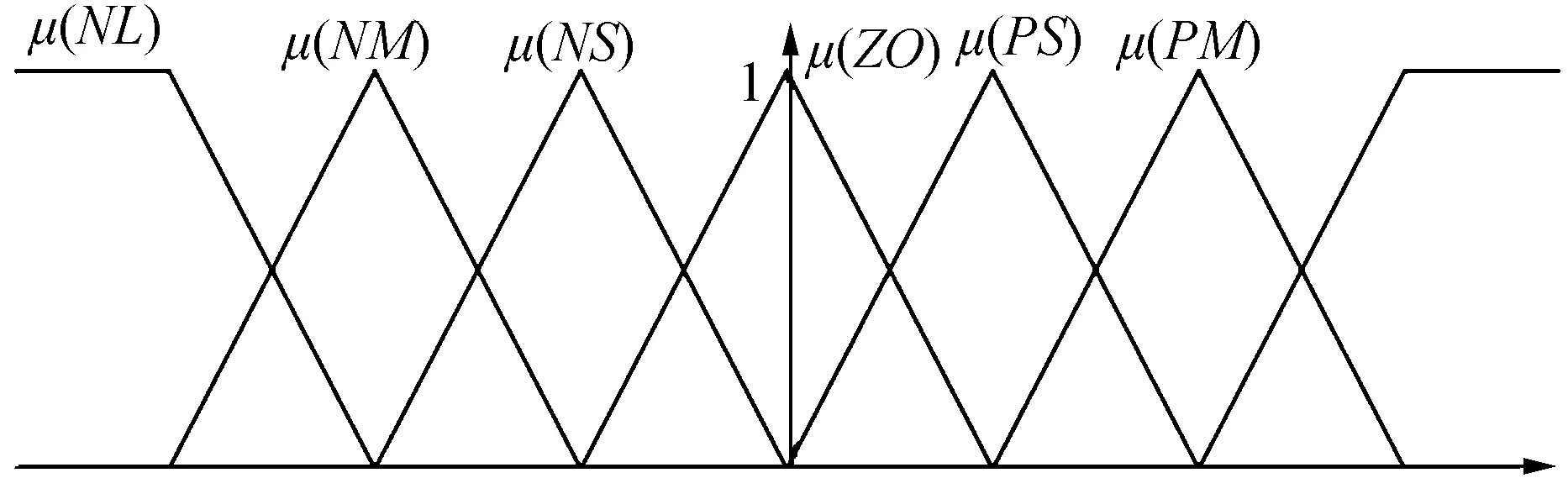
图3　模糊语言描述图

图3中，模糊语言分别定义为：NL(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PL(正大)。它们分别代表论域的某一范围，各个小论域的中心值描述该语言的概率为1，描述其他语言的概率为0，其他对应点的概率描述采用三角形隶属函数MF。

2.2.3模糊规则

根据数学原理和工程经验得到下面的基本规则：

(1)若误差均值Mx很大，则增大平滑参数；

(2)若误差均值Mx很小，则减小平滑参数；

(3)若误差方差Vx很大，则减小平滑参数；

(4)若误差方差Vx很小，则增大平滑参数。

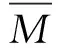
根据基本规则，设计平滑参数的模糊调整规则，描述如下：

如果Mx是Ai，且Vx是Bi，则Cx是Ci。其中，Ai为Mx论域上的模糊值，Bi为Vx论域上的模糊值，Ci为Cx论域上的模糊值。根据模糊化语言集合，其模糊规则如表1所示。

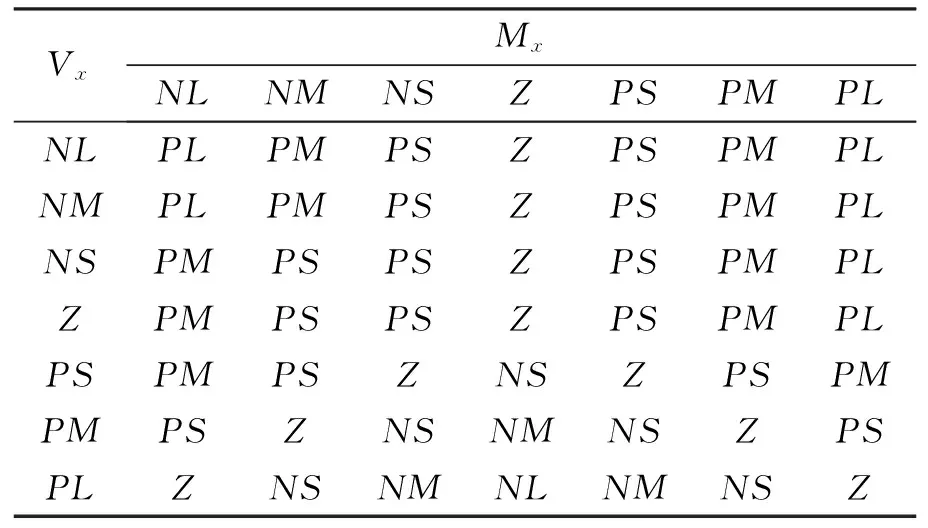
表1　模糊规则表

2.2.4模糊推理

由模糊逻辑推理法[9]可知，对于n条模糊规则可以得到n个输入输出关系矩阵R1，R2，…，Rn，从而由模糊规则的合成算法得到系统总的模糊关系矩阵为

(4)

则对于任意Mx和Vx，其对应的模糊调节器输出Cxij为

Cxij=(Mxi×Vxj)·R

(5)

2.2.5清晰化

对式(5)得到的模糊调节量Cxij再进行精确化计算就可以直接调节被调参数。这里采用加权平均法对模糊输出进行清晰化(即去模糊化)处理，其计算公式为

(6)

3　试　验

将基于模糊理论的平滑方法用于某组网融合系统中，对目标的融合航迹进行实时自适应平滑处理，得到图4和图5中的结果。图4为非机动目标，其中，*为平滑前的融合航迹，o为平滑后的融合航迹。图5为拐弯目标，其中，*为平滑前的融合航迹，o为平滑后的融合航迹。表2、表3对平滑前后航迹误差均值与方差进行比较，其中，误差均值代表航迹的精度，误差方差代表航迹的平滑度。

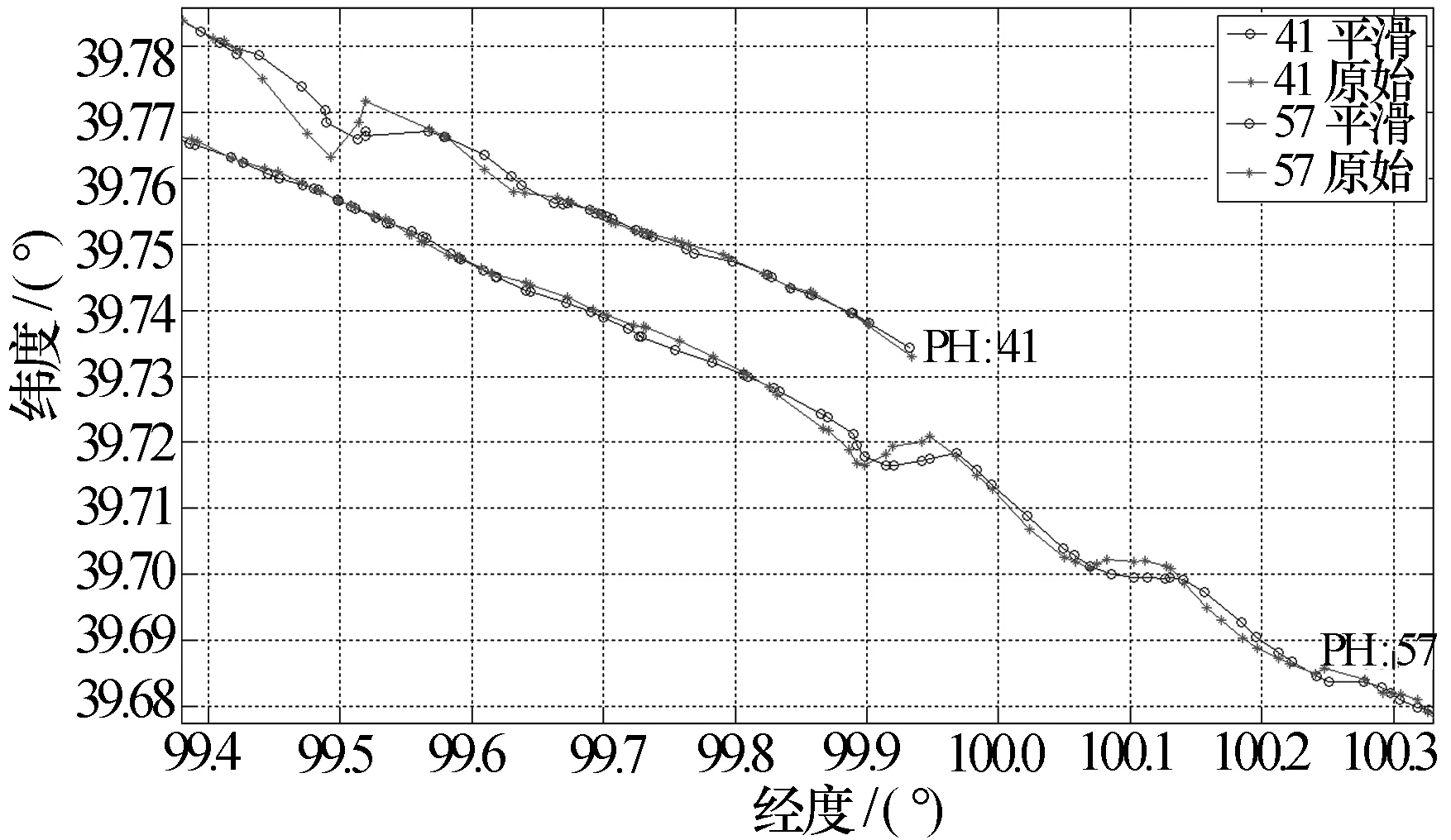
图4　融合航迹平滑前后的轨迹(非机动目标)

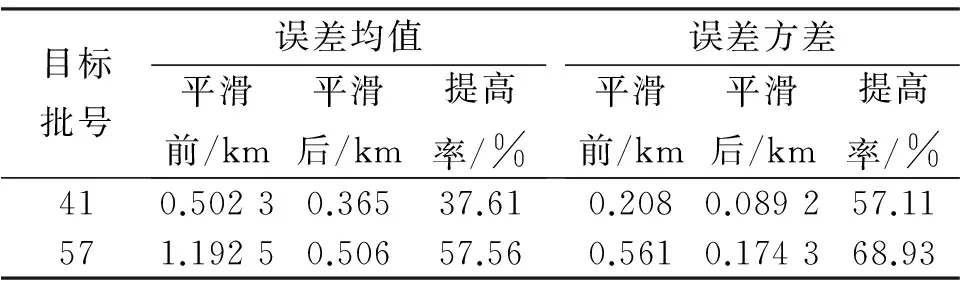
目标批号误差均值平滑前/km平滑后/km提高率/%误差方差平滑前/km平滑后/km提高率/%410.50230.36537.610.2080.089257.11571.19250.50657.560.5610.174368.93

图5　融合航迹平滑前后的轨迹(拐弯目标)

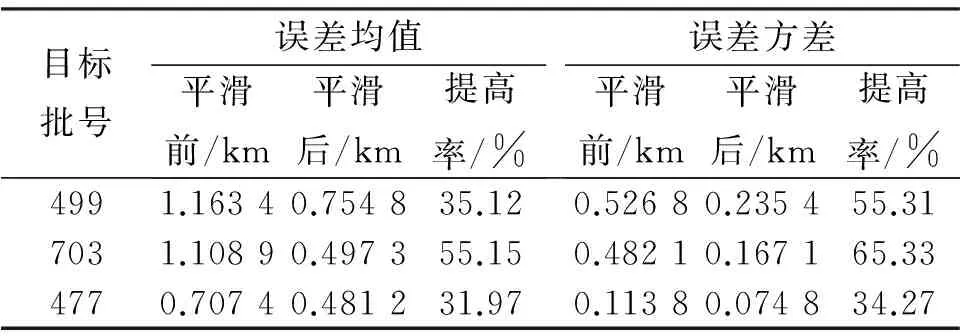
目标批号误差均值平滑前/km平滑后/km提高率/%误差方差平滑前/km平滑后/km提高率/%4991.16340.754835.120.52680.235455.317031.10890.497355.150.48210.167165.334770.70740.481231.970.11380.074834.27

从图4～图5以及表2～表3可以看出：无论对非机动目标还是拐弯目标，文中提出的平滑方法都提高了航迹精度和平滑度，在很大程度上提高了融合航迹质量，为战场侦察提供了高质量、高可靠性的战场态势。

4　结束语

该平滑方法克服了航迹滤波对采样时间的高敏感性，突破了对目标建模思想，从根本上克服了实际环境与数据模型失配引起的滤波发散现象。与其他的平滑方法(如：直线拟合、移动平均、加权平均等)相比，该方法充分利用了目标航迹的历史信息和目标位置的变化趋势，消除了算法对时间的敏感性，大大减少了存储量(与直线拟合、移动平均相比)，提高了计算速度。同时模糊理论的引入，实现了平滑参数的在线智能调整，能较好地提高平滑精度。

[1]诸静. 模糊控制原理与应用[M]. 北京: 机械工业出版社, 1995.

ZHU Jing. Fuzzy control theory and applications[M]. Beijing: China Machine Press, 1995.

[2]ZADEH L A. Fuzzy sets[J]. Information Control, 1965(8): 338-353.

[3]WALTZ E, LLINAS J. Multisensor data fusion[M]. Norwood, MA: Artech House, 1990.

[4]BU Kman S S. Multiple-target tracking with radar applications[M]. Norwood, MA: Artech House, 1986.

[5]张文修, 梁怡. 不确定性推理原理[M]. 西安: 西安交通大学出版社, 1998.

ZHANG Wenxiu, LIANG Yi. Principle of uncertainty reasoning[M]. Xi′an: Xi′an Jiaotong University Press, 1998.

[6]KLEIN L A．Sensor and data fusion concepts and applications[M]. [S.l.]: SPIE Optical Engineering Press, 1999.

[7]章新华. 基于模糊推理规则的舰艇规避策略[J]. 火力与指挥控制, 1995, 20(2): 73-76.

ZHANG Xinhua. Ship-based fuzzy inference rules avoidance strategy[J]. Fire Control and Command Control, 1995, 20(2): 73-76.

[8]BAKI B, KING M L, SNYDER R D, et al. Exponential smoothing model selection for fore-casting[J]. International Journal of Forecasting, 2006, 22(2): 239-247.

[9]韦巍. 智能控制基础[M]. 北京: 清华大学出版社, 2000.

WEI Wei. Intelligent control basis[M]. Beijing: Tsinghua University Press, 2000.

胡昌林男，1977年生，高级工程师。研究方向为多传感器数据融合。

王蕾女，1977年生，副教授。研究方向为自动化控制。

A Method of Adaptive Data Smoothing Based on Fuzzy Theory

HU Changlin1，WANG Lei2

(1. Nanjing Reserach Institute of Electronics Technology,Nanjing 210039, China) (2. School of Automation, Nanjing Institute of Technology,Nanjing 211167, China)

Integration track quality optimization methods in data fusion system of the intelligence radar network is studied. By considering the role of people in the fusion system, by data mining, we start to find ways to optimize the quality of the fused track, and then data adaptive smoothing method based on fuzzy theory proposed. With this method, moving average method is improved and second smoothing method is gotten, also fuzzy theory is used for data adaptive smoothing. The experiments show that this method can greatly improve the quality of the data fusion track quality, providing high-quality, high reliability fusion data for users.

data fusion; adaptive data smoothing; fuzzy reasoning; adaptive adjustment; moving average; data mining

胡昌林Email：56108000@qq.com

2016-03-21

2016-05-23

TN911

A

1004-7859(2016)07-0049-03

DOI：10.16592/ j.cnki.1004-7859.2016.07.012