Matlab在周期信号分解及频谱中的应用

闫红梅, 吴冬梅, 吴延海

(西安科技大学 通信与信息工程学院, 陕西 西安　710054)



Matlab在周期信号分解及频谱中的应用

闫红梅, 吴冬梅, 吴延海

(西安科技大学 通信与信息工程学院, 陕西 西安710054)

利用Matlab对方波、锯齿波、三角波等周期信号进行傅里叶级数分解和合成,直观演示了谐波合成过程和吉布斯现象,并且画出方波分解的三维图形,通过调整视角观察信号时域波形与频域频谱的关系。实践表明,将Matlab引入教学可以帮助学生把握重点、理解难点,激发了学生学习兴趣,起到了很好的教学辅助作用,有效地改善了教学效果。

信号与系统;Matlab; 傅里叶级数; 周期信号分解

信号与系统课程是高等学校电子信息类专业一门重要的专业基础课,在教学计划中起着承前启后的作用,也是相关专业研究生入学考试的必考科目。该课程理论性强,内容抽象,所涉及到的数学知识面广,传统的教学方式仅凭教师讲述和板书推导很难将抽象的概念讲述清楚。美国麻省理工学院公布的教学改革计划(于2011年实施)已经将Matlab引入信号与系统课程辅助教学[1],这一做法也得到国内众多高校教师和学者的共识[2-6]。周期信号的傅里叶级数分解和合成是信号与系统课程的重点和难点之一,通过该内容的学习可使学生建立起信号频谱的概念,同时为进一步学习傅里叶变换和线性时不变系统的频域分析等内容打下基础。很多高校教师将实际案例分析[7-8]和Matlab仿真[9-10]引入课堂教学,对激发学生学习兴趣、提高教学质量都取得了一定的效果。

本文利用Matlab仿真实现了方波、锯齿波和三角波这些具有代表性的周期信号的傅里叶级数分解和合成过程,动态地演示了谐波合成过程和吉布斯现象，画出了方波分解的三维图形,通过改变视角直观地观察时域合成效果和周期信号频谱的特点,使学生对频谱的物理意义有了深入的理解。

1　周期信号的傅里叶级数

1.1傅里叶级数的定义

18世纪法国著名的数学家、物理学家傅里叶(H·Fourier,1768-1830)最初提出傅里叶级数的基本理论[10]。一个满足狄里赫利条件的周期信号f(t),其周期为T,角频率Ω=2π/T,该信号的傅里叶级数展开式为[11]

(1)

其中,傅里叶系数：

(2)

(3)

将式(1)中同频率项合并,可写为

(4)

式中：

(5)

1.2方波信号的傅里叶级数

方波信号是一种基本的周期信号,在理论分析中具有重要的代表性作用。将图1所示的方波信号f(t)展开为傅里叶级数。由式(2)和式(3)可得f(t)的傅里叶系数：

(6)

(7)

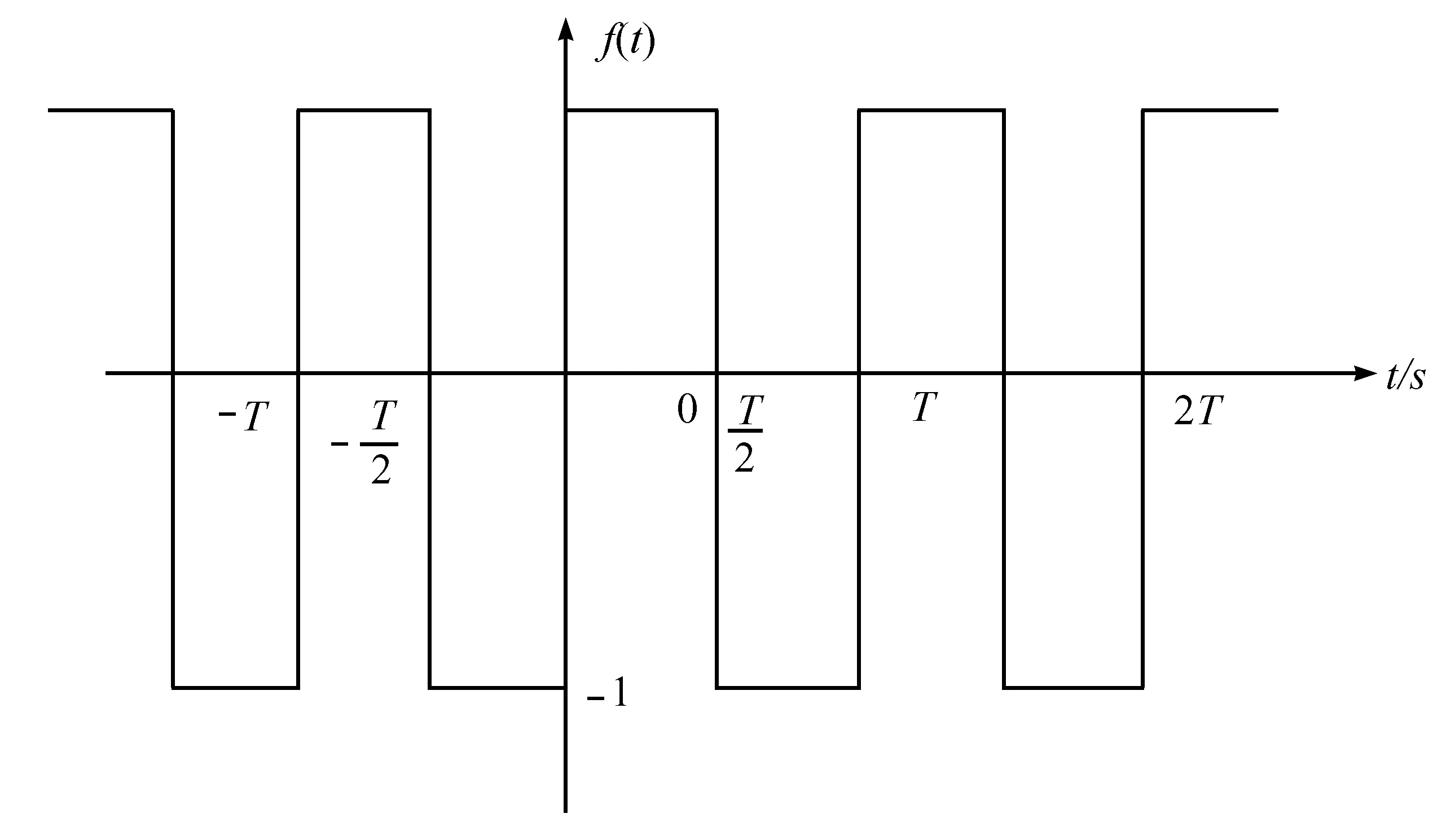
图1　方波信号

将an和bn代入式(1),可得图1所示方波信号的傅里叶级数展开式为

(8)

可见,该方波信号只含1、3、5等奇次谐波分量。

2　利用Matlab分析周期信号的分解与合成

利用Matlab中的guide命令[12]设计出周期信号的分解与合成GUI演示界面。通过下拉框可以选择周期信号的类型为方波、锯齿波或三角波。在文本框中输入谐波次数可以观察不同谐波次数下周期信号分解、合成过程。方波信号的前3次、7次、21次谐波分解及合成图分别如图2中的(a)、(b)、(c)所示,锯齿波和三角波的前21次谐波分解及合成图分别如图2(d)和(e)所示。

由图2中(a)、(b)、(c)可见：(1)低频分量幅度较大、变化较慢,构成信号的主体,高频分量幅度较小、变化较快,影响波形的细节。这一基本理论也可用于图像压缩,在保证一定图像质量的前提下,丢弃掉图像的部分高频分量,保留低频分量,可以减小图像大小,节省存储空间和传输带宽；(2)所含高次谐波分量越多,合成波形越逼近方波信号。但随着谐波次数的增加,在间断点处存在的过冲幅度并未明显减小。可以证明,即使合成波形所含谐波次数n→,在间断点处的幅度仍有约9%的偏差,这种现象称为吉布斯(Gibbs)现象。在n取很大时,间断点尖峰下的面积很小以致于趋于零,因而在均方意义上,合成波形与原方波的真值之间没有区别。

由图2(d)、(e)可以看出,锯齿波的合成波形存在吉布斯现象,而三角波的合成波形不存在吉布斯现象,说明吉布斯现象是由间断点引起的。

3　利用Matlab分析周期信号的频谱

利用Matlab编写程序,在时间-频率-幅度的三维空间画出图1所示方波信号分解为11次谐波分量的图形,如图3(a)所示。利用Matlab的图形旋转按钮调整视角,旋转为时间-幅度的二维图形,如图3(b)所示,其中红色波形为合成波形,其他为各谐波分量波形,结论与前述相同。再旋转为频率-幅度的二维图形,如图3(c)所示,图中各细线即表示各谐波分量的幅度,此图为方波信号的幅度谱。图3(c)虽然是方波信号的幅度谱,但其具有一般性,代表了一般周期信号频谱的特点：(1)离散性,各谱线是离散的,以基波频率Ω=2π/T为间隔；(2)谐波性,各谱线只出现在各次谐波频率处,即ω=nΩ；(3)收敛性,各次谐波的振幅随着谐波次数的增高而逐渐减小。

图2　周期信号的分解与合成

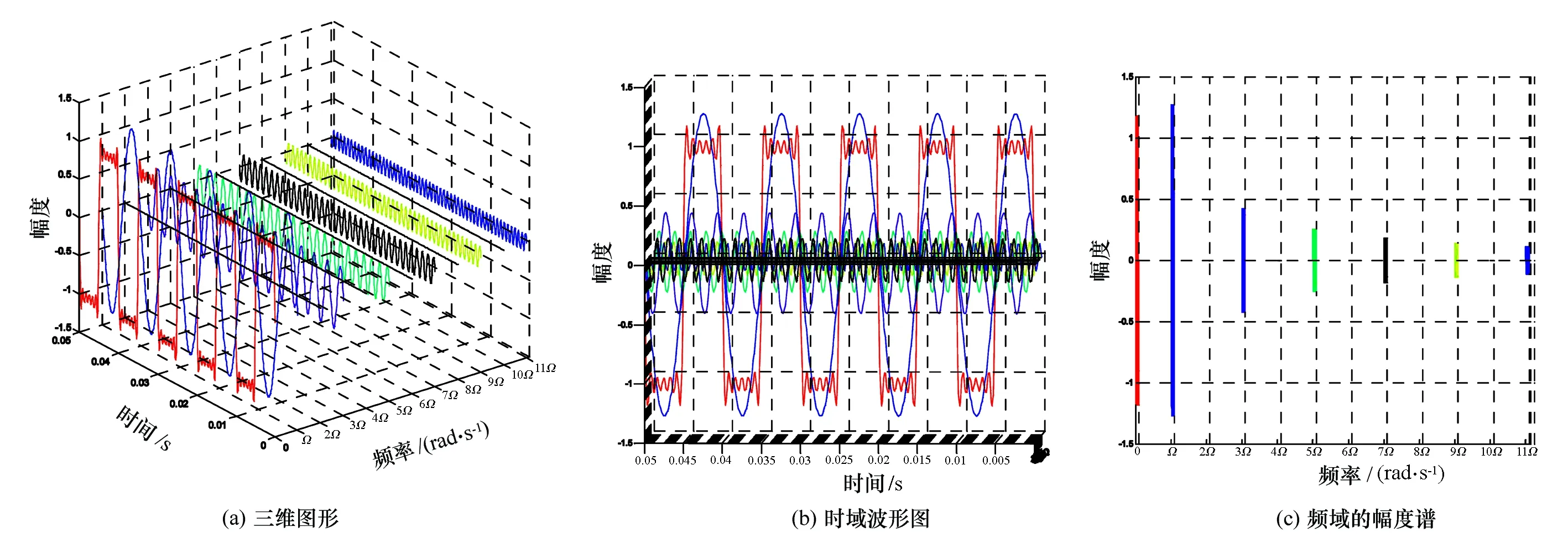
图3　不同角度下的方波分解图

4　结语

Matlab具有强大的计算能力和绘图能力,GUI可视化界面具有良好的交互性和直观性。在教学中利用Matlab进行仿真,直观地演示周期信号分解及合成过程以及信号时域波形与频域频谱的关系,可以帮助学生理解傅里叶级数这一抽象的概念,有助于学生进一步学习傅里叶变换及频域分析方法。将Matlab引入信号与系统课程教学,可以激发学生学习兴趣,提高课堂教学质量,起到了很好的教学辅助作用。

References)

[1] 郑君里,谷源涛.信号与系统课程历史变革与进展[J].电气电子教学学报,2012,34(2):1-6.

[2] 杜世民,杨润萍.基于MatlabGUI的“信号与系统”教学仿真平台开发[J].实验技术与管理,2012,29(3):87-90.

[3] 金波.基于Matlab的“信号与系统”实验演示系统[J].实验技术与管理,2010,27(12):104-107.

[4] 马占敖,李红.“信号与系统”课程中的MATLAB的应用[J].长春理工大学学报,2011,6(5):132-133.

[5] 全星慧,周围,韩建，等.基于Matlab的信号与系统实验平台设计[J].现代电子技术,2014,37(22):88-90.

[6] 李念念,张红梅.基于MATLABGUI的信号与系统分析软件开发[J].工业控制计算机,2011,24 (3):19-21.

[7] 向倩.聆听傅立叶级数：《信号与系统》教学改革漫谈[J].武汉大学学报：理学版,2012,58(增刊2):120-124.

[8] 张锐,袁丽英.信号与系统课程中对周期信号频谱分析的理解[J].高等函授学报：自然科学版,2012,25(2):30-32.

[9] 韩晓霞,高月华,陈雷.连续时间周期信号频域分析的MATLAB实现[J].河北软件职业技术学院学报,2013,15(1):52-54.

[10] 邓新浦,吴京.傅里叶级数的起源、发展与启示[J].电气电子教学学报,2012,34(5):1-4.

[11] 吴大正,杨林耀,张永瑞.信号与线性系统分析[M].4版.北京：高等教育出版社,2005.

[12] 梁虹.信号与系统分析及MATLAB实现[M].北京：电子工业出版社,2002.

ApplicationofMatlabinperiodicsignaldecompositionandspectrum

YanHongmei,WuDongmei,WuYanhai

(SchoolofCommunicationandInformationEngineering,Xi’anUniversityofScienceandTechnology,Xi’an710054,China)

ThispaperusesMatlabtosimulateFourierseriesdecompositionandsynthesisofsquarewave,sawtoothwaveandtrianglewave,andpresentsalivelyanddirectviewofharmonicsynthesisprocessandtheGibbsphenomenon.ItusesMatlabtodrawthesquarewavedecomposition3Dgraphicsandanalysestherelationshipbetweensignalwaveformandspectrumbyadjustangleofview.TheteachingactivityshowsthataddingthevividMatlabsimulationintotheabstracttheoryteachingishelpfultodeepenstudents’understanding,masterthecoursecontents,stimulatetheirlearninginterestandimprovetheteachingeffecteffectively.

signalandsystem；matlab；fourierseries；periodicsignaldecomposition

DOI:10.16791/j.cnki.sjg.2016.05.012

2015- 11- 30修改日期：2015- 12- 29

2015年度陕西本科高校省级教学团队项目——信号处理系列课程教学团队项目(陕教高[2015]13号)；西安科技大学2014年度校级教育教学改革与研究项目“‘信号与系统’课程多维立体教学研究”(JG14106)；2013年度陕西省省级质量工程——基于CDIO的电子信息类专业人才培养模式创新实验区项目(陕教高[2013]28号)

闫红梅(1978—)，女，陕西商洛，硕士，讲师，主要从事信号处理与人工神经网络方面的教学和研究工作.

E-mail：yhm523@163.com

TN911.6;TP391.9

A

1002-4956(2016)5- 0037- 03