小兴安岭阔叶红松林木本植物种-面积关系

王睿智, 国庆喜

东北林业大学, 哈尔滨　150040



小兴安岭阔叶红松林木本植物种-面积关系

王睿智, 国庆喜*

东北林业大学, 哈尔滨150040

种-面积关系研究是了解植物群落结构的重要途径，是群落生态学的基本问题。不同的研究方法对种-面积关系影响很大。利用黑龙江省小兴安岭两个10.4 hm2样地和5个1.0 hm2样地的调查数据，采用移动窗口法确定各样地的最小取样面积，避免了巢式取样法及随机样方法的不足。并采用4种种-面积关系模型进行拟合，评价各关系模型的适合度。在此基础上，基于最小面积进行模拟随机取样，探讨取样大小对物种数估计精度的影响。研究结果表明：由于拟合曲线模型的适用性及曲线外推可靠性问题的存在，采用拟合曲线的方法所估计的最小面积与实际值偏差较大。实际调查得到的各样地最小面积40 m×40 m—45 m×45 m，说明小兴安岭地区阔叶红松林群落所需的最小面积基本一致，但各样地群落结构的差异却在对取样数量的要求上体现出来。其中丰林与大亮子河样地物种数分布相对均匀，所需最小样方数量较少；而方正与胜山样地物种数分布异质性较大，差异的机理还有待于进一步研究。

最小面积； 取样数量； 种-面积关系； 阔叶红松林

种-面积关系描述的是植物群落中物种数随样地面积的增加而变化的规律[1-3]，这甚至已经成为“植物群落生态学中的定律之一”[4]。在不同尺度中，影响生物多样性分布格局的因素不同，因此种-面积关系表现出明显的尺度效应[5]。理论上，生物群落的种-面积关系主要与种-多度分布和物种的空间分布有关[5]。在均质生境中，样方所包含的个体数与取样面积成正比[6]，物种数随取样面积的增加而增加[7]，而取样面积所包含的物种数主要取决于所有个体在不同物种之间的分配，物种在空间分布上聚集程度越高，小面积中可观察的物种会越少，物种数随面积增加的速率会下降[8]。种-面积曲线或种-面积关系是群落调查的重要内容之一[9]。多数研究认为，应当根据种-面积曲线所确定的群落最小面积作为临界取样面积，因为最小面积可以使群落的种类组成和结构得以充分表现[10]，是反映群落种类组成和结构特征的最小地段[11]。它在很大程度上取决于群落类型，并且变化的幅度很大。故确定植物群落的最小面积是研究植物群落，尤其是定量数据获取的首要步骤[12]。而研究一个区域的物种数与区域面积分布关系，对于该地区物种保护及生物多样性的维持都具有极其重要的意义[13]。

目前，对于群落最小面积和临界抽样面积的研究已有很多报道[2,4-5,8,14-25]，但由于调查工作量的限制，只能采用有限的样方面积和数量，并依靠种-面积关系拟合曲线来得到最小面积值。因为植被群落的空间异质性普遍存在，并且由于取样面积的扩大使研究样地包含更多的生境类型并且增加了生境的异质性[5]，这些因素会引起物种数量的变化。因此取样密度不够，会对种-面积关系的研究带来较大干扰。即使是同一植被类型，由于空间样方设置的差异，研究结果也往往截然不同[4]。同样，在得到最小面积数据的基础上，究竟多大的取样数量才能满足群落调查结果的精度要求，有待进一步探讨。

近年来，姜俊等[13]利用大样地的数据优势探讨了吉林蛟河针阔混交林样地植物种-面积关系，徐丽娜等[26]基于小兴安岭凉水阔叶红松林的大型固定监测样地数据构建了种-面积曲线，进而研究了阔叶红松林的物种组成与群落结构，随着这些基于大型样地的调查研究的开展，为研究种-面积关系问题提供了新的途径。本文运用在黑龙江省小兴安岭各地设置的7个1.0—10.4 hm2的阔叶红松林样地调查数据，确定小兴安岭各地红松林群落的最小面积，并通过模拟随机抽样探讨合理的取样数量，以便于揭示各地红松林群落结构的差异，以期为该区域生物多样性的保护及经营管理提供理论依据。

1　研究区概况

本研究区域位于黑龙江省东北部小兴安岭(北纬46°28′—49°21′，东经127°42′—130°14′)，该区域属北温带大陆季风气候区，四季分明，最冷月1月平均气温-20—-25℃，最低温度可达-40℃，最热月7月平均气温19 —21℃左右，最高温度可达31℃，极端最高气温为35℃，全年平均气温-1—1℃；年降水量为500—700 mm；土壤类型为典型暗棕壤，厚度超过50 cm，肥力高。小兴安岭在中国植被区划上属于温带针阔混交林区域内的北部地区，原生地带性植被是红松为主的温带阔叶红松林，木本植物种类多样，乔木树种主要包括红松(Pinuskoraiensis)、紫椴(Tiliaamurensis)、枫桦(Betulacostata)、白桦(Betulaplatyphylla)、臭冷杉(Abiesnephrolepis)、兴安落叶松(Larixgmelinii)、蒙古栎(Quercusmongolica)、裂叶榆(Ulmuslaciniata)、红皮云杉(Piceakoraiensis)、鱼鳞云杉(Piceajezoensis)、水曲柳(Fraxinusmandshurica)、黄菠萝(Phellodendronamurense)、胡桃楸(Juglansmandshurica)、色木槭(Acermono)和大青杨(Populusussuriensis)等，灌木主要包括暴马丁香(Syringareticulata)、毛榛子(Corylusmandshurica)、瘤枝卫矛(Euonymusverrucosus)、和东北鼠李(Rhamnusyoshinoi)等。

2　研究方法

2.1样地设置及调查

在小兴安岭的凉水国家级自然保护区与胜山国家级自然保护区内分别建立一个10.4 hm2(400 m×260 m)的阔叶红松林固定样地，将其划分成260个20 m×20 m的连续样方，在每个20 m×20 m样方中进一步划分出16个5 m×5 m的亚样方。在方正县双子山国家森林公园、汤旺河林业局守虎山林场、汤原县大亮子河国家森林公园、朗乡林业局的东折棱河林场和丰林国家级自然保护区分别设置一个1.0 hm2(100 m×100 m)阔叶红松林样地进行调查，划分标准以凉水和胜山两个样地为参照。调查并记录上述7个样地内所有胸径(DBH)≥1.0 cm的木本植物个体的种类、胸径(DBH)以及坐标等信息。这7个样地位于不同地理位置，分布在小兴安岭各个地区，其海拔、气候条件等自然条件存在差异，同时各样地物种组成也存在不同，7个样地内物种数各不相同，但共有物种只有红松，枫桦，裂叶榆，色木，紫椴，暴马丁香，毛榛子，山梅花这8种。以上这些因素都会造成取样差异，因而收集这7个样地数据来代表小兴安岭地区(表1)。

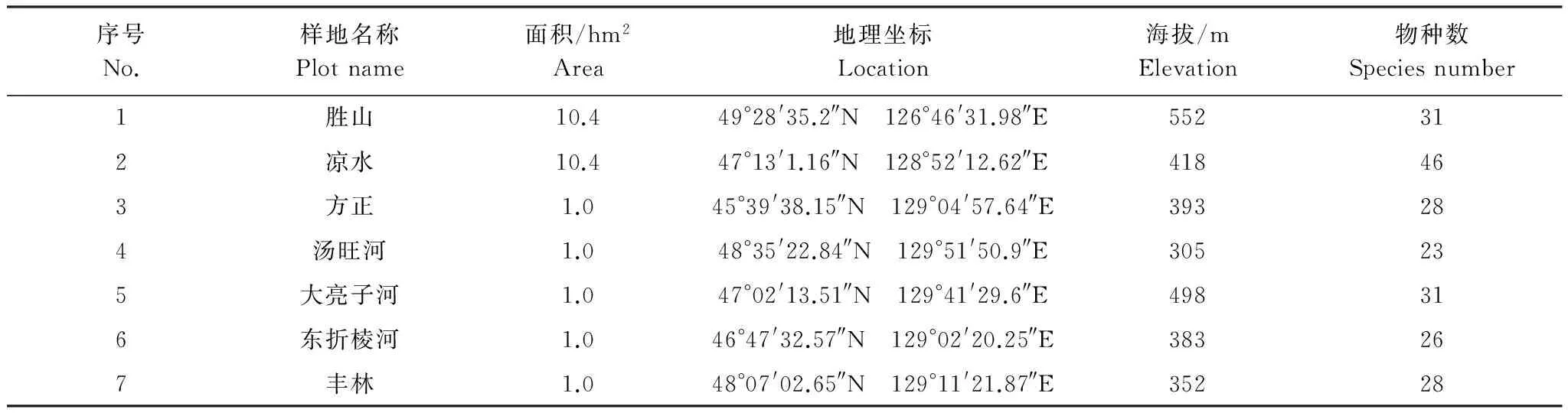
表1　样地概况Table 1　Introduction to the plots

2.2种-面积关系的确定

以5 m×5 m为基本单位设置正方形样方。随样方边长依次增加5 m而扩大样方面积，样方面积依次为5 m×5 m、10 m×10 m、15 m×15 m、…、100 m×100 m。为了统计每种面积样方内的木本植物物种数，采用了移动窗口法，以10 m×10 m样方为例，在样地左下角设置10 m×10 m的搜索窗口，统计窗口内物种数，然后整个窗口依次向右或向上移动5 m，每次移动后再次统计窗口内的物种数，从而遍历整个样地，统计所有这一面积样方所含物种数的平均值。最后将平均值随样方面积增加而变化的关系绘制成种-面积曲线，按照曲线趋于平缓时的样方面积来确定最小面积。

在种-面积关系的研究中，普遍采用饱和种-面积曲线拟合的方法，通过这种方法可以估计出群落的总物种数，这样在计算临界抽样面积时就不需要事先知道群落总物种数[22]，从而减少外业调查的工作量。这里选用常用的4种饱和曲线模型来模拟各样地的种-面积关系[7]：

(1)

(2)

S=c-ae-bA

(3)

(4)

式中，A为样方面积，S为样方中出现的物种数，a、b、c是待定参数。方程的拟合利用SPSS17.0软件来完成。

求解最小面积就是得到群落总物种数一定比例p(0﹤p﹤1)的物种所需要的面积，与4种饱和曲线模型相对应的计算公式分别为：

(5)

(6)

(7)

(8)

3　结果与分析

3.1最小面积的确定

通过实测数据而得到的各样地阔叶红松林木本植物物种数与取样面积的关系见图1。对于种-面积关系的研究来说，物种数随面积扩大而增加，起初增加很快，以后逐渐缓慢[27]。

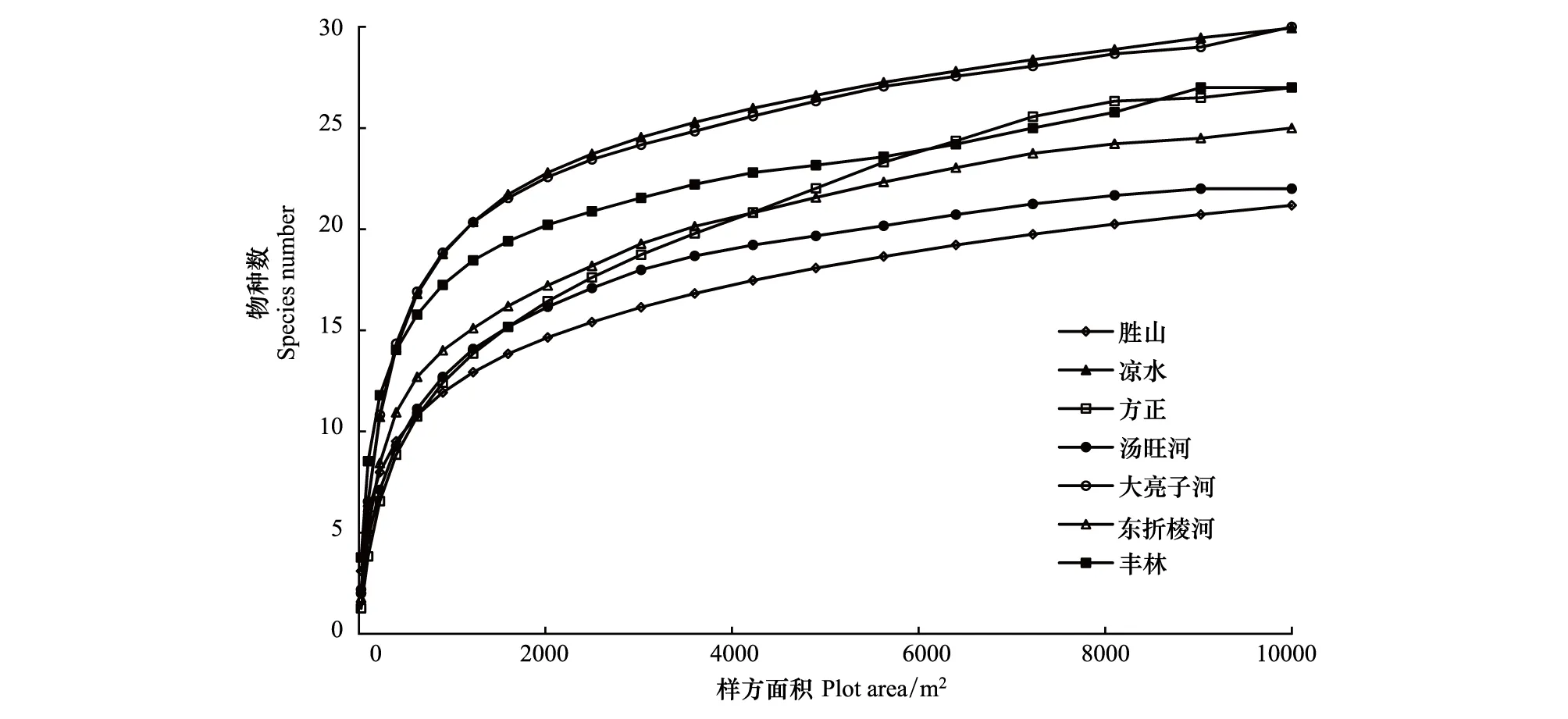
图1　种-面积曲线Fig.1　Species-area curves

从7个样地的种-面积关系曲线来看，基本可以确定在面积达到900—1225 m2时，曲线由陡峭上升逐渐趋于平缓。对于胜山与凉水这两个10.4 hm2的样地，样方面积在2025 m2时，曲线斜率开始相对稳定；而对于其他5个1.0 hm2的样地，样方面积在1600 m2时，曲线斜率开始相对稳定。因此依据实测数据可以初步将胜山与凉水样地最小面积定为2025 m2，对应的样方大小为45 m×45 m；将其他5个样地最小面积定为1600 m2，对应的样方面积为40 m×40 m。最小面积对应的物种数分别为胜山15、凉水23、方正15、汤旺河16、大亮子河22、东折棱河16、丰林19；占样地总物种数的比例分别为胜山48.4%、凉水50%、方正53.6%、汤旺河69.6%、大亮子河70.9%、东折棱河61.5%、丰林67.9%。

在Archibald[28]的研究中发现，在占群落总物种数50%对应的面积上常见种就总是出现，因此将这个面积定义为群落最小面积。按照这个观点，本文中确定的最小面积上的物种数基本占到相应总物种数的50%以上，故小兴安岭阔叶红松林木本植物的最小取样面积为40 m×40 m—45 m×45 m。

利用移动窗口法得到的种-面积关系数据，根据种-面积曲线模型(1)—(4)拟合得到相应的方程见表2。所列方程对种-面积关系拟合的R2值均在0.9以上，综合比较4个饱和曲线模型，模型(1)和(3)对7个样地的种-面积关系拟合效果更好一些。

表2　种-面积曲线拟合结果Table 2　Modeling results of species-area curves

取比例因子p分别为0.6、0.8、0.9，即最小面积分别包含总物种数的60%、80%、90%时所求得的每个饱和曲线模型的最小面积(表3)。由表3可以看出，在7个样地中，以p=0.6拟合确定的最小面积明显小于依据实际数据(移动窗口法)确定的值。只有当比例因子p取0.8—0.9时，所确定的最小面积才与实际调查值接近。而通过实际数据利用移动窗口法确定的最小面积所包含的物种数则分布在48.4%—70.9%之间。通过拟合曲线模型得到的最小面积远小于实际调查结果；即使通过拟合曲线模型所确定的最小面积与实际调查结果相同，但在其确定的最小面积内所包含的物种数比例估计值远大于实际的物种数比例。

表3　种-面积曲线计算的最小面积Table 3　Minimum sampling area calculated by species-area curves

3.2取样数量的确定

虽然确定了各样地的最小面积，但并不意味着仅仅用1个达到最小面积的样方就能得到可靠的物种数估计结果。根据各个样地的实测数据，如果仅采用1个最小面积样方，物种数估计结果与其平均值存在很大偏差，其最大相对误差分别为胜山56%、凉水40%、方正64%、汤旺河30%、大亮子河21%、东折棱河30%、丰林18%。可见必须设置一定数量的样方，才能将误差限制在一定范围内。

为了探讨取样数量对物种数估计精度的影响，针对最小面积样方进行模拟抽样。在样地中随机抽取被确定为最小取样面积的正方形样方，每次随机抽取的样方数量依次设置为1、2、3、…、20。为尽量消除抽样的随机误差，将每种样方数量的取样操作重复3000次，每次重复操作都得到各样方物种数的平均值。统计这3000次重复操作所得到的所有平均值的最大值Nmax与最小值Nmin。计算最大值与最小值同最小面积所含物种数实测值之间的相对误差Emax、Nmin，二者间的最大值为最大相对误差，其公式如下：

(9)

(10)

针对各样地最小面积样方取样数量与最大相对误差之间关系建立曲线图(图2)。虽然各样地最小面积基本一致，但对取样数量要求则差异很大。以最大相对误差20%为例，如果达到这一精度，丰林样地只需1个最小面积样方就能达到，而方正样地则需要至少17个。在理论上取样的样方数愈多愈能真实地反应样地中植物种类的数量，但在实际工作中可以发现，当样方数达到某一值时，最大相对误差曲线下降的幅度开始趋于平缓。因此在保证精度的基础上可以设置一个最小的取样数量以减少工作量。

图2　样方数与最大相对误差关系图Fig.2　Relationship of maximum relative error between sample size

4　结论与讨论

本文运用分布于小兴安岭各地的1.0—10.4 hm2样地数据，探讨了各样地阔叶红松林木本植物种-面积关系。研究表明，在面积达到900—1225 m2时，曲线由陡峭上升逐渐趋于平缓。对于其中5个1.0 hm2的样地，最小面积确定为1600 m2，对应的样方面积为40 m×40 m。对于两个10.4 hm2的样地，最小面积确定为2025 m2，对应的样方面积为45 m×45 m。这与孙中伟[29]对长白山北坡椴树红松林群落研究得到的乔木树种的抽样面积结果(40 m×40 m)和郝占庆[30]对长白山北坡阔叶红松林群落研究得到的最小取样面积(40 m×40 m)基本一致。与以往有关阔叶红松林的研究报道[13,26]不尽相同，因为研究方法、群落具体状况结构等都有区别。尽管小兴安岭各地阔叶红松林群落结构等存在差异，但最小面积却基本一致。

姜俊等[13]利用大样地的数据优势探讨了吉林蛟河针阔混交林样地植物种-面积关系，其研究结果表明不同取样方法对种-面积关系有显著影响，并指出相比巢式取样法，随机取样方法拟合效果更优。本文采用了移动窗口法探讨物种数与样方面积的关系，与以往的巢式样方法和组合样方法相比，移动窗口法不是在同一地段逐渐扩大样方面积，或是将一定数量随机设置的小样方相加，它通过将大样地中不同取样面积的样方无遗漏地进行统计，计算出该面积下的平均物种数，从而避免了由于群落空间异质性带来的取样误差对种-面积关系造成的干扰 。

本文同时利用移动窗口法得到的种-面积关系数据(以保证拟合曲线所用数据不存在取样误差)探讨了4种常用饱和种-面积关系曲线模型对最小面积的确定结果。发现通过模型拟合而确定的最小面积与依靠实际数据确定的结果之间存在差距。依据实际数据确定的最小面积仅包含群落总物种数的60%左右，如果按照包括群落60%物种数的要求，通过种-面积曲线拟合确定的最小面积则明显低于实际的调查结果。只有在按照包括群落80%—90%物种数的要求进行拟合，其结果才与实际值接近，但实际上这个最小面积并没有包含如此高比例的物种数。可见在本文所研究地区采用曲线拟合的途径似乎并不适宜。之所以出现这一现象，可能是受到饱和种-面积曲线模型对所研究群落的适用性，以及种-面积曲线外推的可靠性的影响，饱和种-面积曲线模型不需要确定群落总物种数，只是通过曲线外推来确定最小面积[22]。然而在没有较大把握的情况下，种-面积曲线的外推是需要慎重考虑的。以往对阔叶红松林的研究中，通过种-面积曲线模型确定的最小面积完全取决于比例因子p，要求精度高，p就取得大一些，所需要的最小面积也就大一些，但是却往往高估了最小面积样方内物种数占总物种数的比例，这是在以后的研究中需要注意的。

本文同时对最小面积样方的取样数量进行了探讨。通过计算不同取样数量得到的样方物种平均数对实测值的最大相对误差，建立其与取样数量的关系。尽管各样地最小面积接近一致，但各样地阔叶红松林群落结构的差异却在对取样数量的要求上体现出来。其中丰林与大亮子河样地物种数分布相对均匀，所需最小面积的样方数量较少；而方正与胜山样地物种数分布异质性较大，这是否与样地内作为建群种的红松个体的斑块分布有关系还需要进一步探讨。

[1]Lomolino Mark V. Ecology′s most general, yet protean pattern: The species-area relationship. Journal of Biogeography, 2000, 27(1): 17-26.

[2]Barkman J J. A critical evaluation of minimum area concepts. Vegetatio, 1989, 85(1/2): 89-104.

[3]Bunge J, Fitzpatrick M. Estimating the number of species: A review. Journal of the American Statistical Association, 1993, 88(421): 364-373.

[4]Wade B. Worthen. Community composition and nested-subset analyses: basic descriptors for community ecology. Oikos, 1996, 76(3): 417-426.

[5]唐志尧, 乔秀娟, 方精云. 生物群落的种-面积关系. 生物多样性, 2009, 17(6): 549-559.

[6]He F L, Legendre P. On species-area relations. The American Naturalist, 1996, 148(4): 719-737.

[7]Samuel M Scheiner. Six types of species-area curves. Global Ecology and Biogeography, 2003, 12(6): 441-447.

[8]He F L, Legendre P. Species diversity patterns derived from species-area models. Ecology, 2002, 83(5): 1185-1198.

[9]方精云, 王襄平, 沈泽昊, 唐志尧, 贺金生, 于丹, 江源, 王志恒, 郑成洋, 朱江玲, 郭兆迪. 植物群落清查的主要内容、方法和技术规范. 生物多样性, 2009, 17(6): 533-548.

[10]汤孟平, 周国模, 施拥军, 陈永刚, 吴亚琪, 赵明水. 天目山常绿阔叶林群落最小取样面积与物种多样性. 浙江林学院学报, 2006, 23(4): 357-361.

[11]宋永昌. 植被生态学. 上海: 华东师范大学出版社, 2001.

[12]邓红兵, 吴刚, 郝占庆, 王庆礼, 代力民, 高林, 王建中. 马尾松-栎类天然混交林群落最小面积确定及方法比较. 生态学报, 1999, 19(4): 499-503.

[13]姜俊, 张春雨, 赵秀海. 吉林蛟河42 hm2针阔混交林样地植物种-面积关系. 植物生态学报, 2012, 36(1): 30-38.

[14]陈泓, 黎燕琼, 郑绍伟, 王玲, 何飞, 刘军, 慕长龙. 岷江上游干旱河谷灌丛群落种-面积曲线的拟合及最小面积确定. 生态学报, 2007, 27(5): 1818-1825.

[15]石翠玉, 杜凡, 王娟, 杨宇明. 高黎贡山生物多样性研究——Ⅰ中山湿性常绿阔叶林最小取样面积研究. 西南林学院学报, 2007, 27(1): 11-14, 44-44.

[16]要元媛, 闫明, 毕润成. 山西霍山植物群落种-面积曲线与物种多样性的关系. 生态学杂志, 2013, 32(1): 39-44.

[17]余世孝, 宗国威, 陈兆莹, 臧润国, 杨应承. 随机与系统取样的生态学信息量比较. 植物生态学报, 1998, 22(5): 473-480.

[18]戴小华, 余世孝. 海南霸王岭热带雨林植被取样技术研究. 热带亚热带植物学报, 2004, 12(5): 405-410.

[19]朱华, 王洪, 李保贵, 许再富. 滇南热带雨林物种多样性的取样面积探讨. 生物多样性, 1998, 6(4): 241-247.

[20]代力民, 王青春, 邓红兵, 陈高, 王庆礼. 二道白河河岸带植物群落最小面积与物种丰富度. 应用生态学报, 2002, 13(6): 641-645.

[21]吴晓莆, 朱彪, 赵淑清, 朴世龙, 方精云. 东北地区阔叶红松林的群落结构及其物种多样性比较. 生物多样性, 2004, 12(1): 174-181.

[22]刘灿然, 马克平, 于顺利, 王巍. 北京东灵山地区植物群落多样性研究Ⅶ. 几种类型植物群落临界抽样面积的确定. 生态学报, 1998, 18(1): 15-23.

[23]刘灿然, 马克平, 于顺利, 王巍. 北京东灵山地区植物群落多样性研究Ⅵ. 几种类型植物群落物种数目的估计. 生态学报, 1998, 18(2): 138-150.

[24]张蕊, 陈军强, 侯尧宸, 马丽娜, 丁路明, 龙瑞军, 尚占环. 亚高山草甸植物群落植物物种数与取样面积的关系. 生态学杂志, 2013, 32(9): 2268-2274.

[25]Jay R Malcolm, Liu C R, Ronald P Neilson, Lara Hansen, Lee Hannah. Global warming and extinctions of endemic species from biodiversity hotspots. Conservation Biology, 2006, 20(2): 538-548.

[26]徐丽娜, 金光泽. 小兴安岭凉水典型阔叶红松林动态监测样地: 物种组成与群落结构. 生物多样性, 2012, 20(4): 470-481.

[27]张金屯. 数量生态学(第2版). 北京: 科学出版社, 2011.

[28]Archibald E E A. The specific character of plant communities: II. A quantitative approach. Journal of Ecology, 1949, 37(2): 274-288.

[29]孙中伟, 赵士洞. 长白山北坡椴树阔叶红松林群落特征. 生态学杂志, 1995, 14(5): 26-30.

[30]郝占庆, 赵士洞, 陶大力, 王淼. 长白山北坡椴树红松林高等植物物种多样性. 生态学杂志, 1993, 12(6): 1-5.

Woody plants species-area relationships in a broad-leaved Korean pine forest in the Xiaoxing′an Mountains

WANG Ruizhi, GUO Qingxi*

NortheastForestryUniversity,Harbin150040,China

The species-area relationship is an important approach for understanding the structure of the plant community, which represents a fundamental issue in ecology, and is an important component of community surveys. The minimum sampling area of a community can be determined by a species-area curve. However, different sampling methods have dramatic effects on the species-area relationship. Previous studies have shown that the minimum sampling area can be determined by species-area relationship models (e.g., logarithmic function, power function, and logistic function), which are constructed from nested plots and quadrate combination methods. However, the forms and parameters of the species-area relationship models vary with sampling method, regional location, and spatial scale. The nested plot method may increase the probability of appearance of rare species, resulting in exaggeration of the number of species, while the quadrate combination method may neglect the aggregation distribution. Therefore, further research is needed to develop methods with decreased uncertainty. Here, based on the inventory data from two 10.4 hm2plots (Shengshan and Liangshui) and five 1.0 hm2plots (Fangzheng, Tangwanghe, Daliangzihe, Dongzhelenghe, and Fenglin) in the broad-leaved Korean pine (Pinuskoraiensis) mixed forests in Xiao Xing′an mountains, Heilongjiang Province, the minimum sampling areas were determined by species-area curves with the moving window method. This method overcame the limitations of the nested sampling and quadrate combination methods and prevented the interference of sampling error on the species-area relationship caused by the community spatial heterogeneity. Additionally, the species-area curves of the seven plant communities were fitted with four saturation curve models to simulate the minimum sampling areas, and the suitability of these fits was evaluated. Furthermore, random sampling simulation was carried out with the minimum sampling area to examine the effects of sampling number on the accuracy of the species number estimation. The results showed that the measured minimum sampling areas of the seven forest communities with the moving window method varied from 40 m × 40 m to 45 m × 45 m, demonstrating that the minimum sampling areas of the broad-leaved Korean pine forest communities were similar. The R2values of the four species-area relationship models were all greater than 0.8 for the seven plots, but the minimum sampling areas determined by the models differed greatly from that measured because of the suitability of the models and the reliability of the curve extrapolation. Moreover, the proportions of the species of minimum sampling areas to that of the entire plot were overestimated by the models. By simulating the process of random sampling, we examined the effects of sampling number on the accuracy of species number estimation and found that the differences in community structures could be reflected in the demands of sampling numbers. Plots at Fenglin and Daliangzihe required only a small number of samples, indicating an even spatial distribution of species. However, the plots at Fangzheng and Shengshan required a large number of samples, indicating high spatial heterogeneity in the species distribution. Further studies are required to determine the mechanisms responsible for this difference.

minimum sampling area; sampling size; species-area relationship; broad-leaved Korean pine forest

10.5846/stxb201410282107

国家自然科学基金项目(31210103911)

2014-10-28; 网络出版日期:2015-10-28

Corresponding author.E-mail: gqx@nefu.edu.cn

王睿智, 国庆喜.小兴安岭阔叶红松林木本植物种-面积关系.生态学报,2016,36(13):4091-4098.

Wang R Z, Guo Q X.Woody plants species-area relationships in a broad-leaved Korean pine forest in the Xiaoxing′an Mountains.Acta Ecologica Sinica,2016,36(13):4091-4098.