北京市降雨量与参考作物腾发量多时间尺度的集对分析

张金萍， 林小敏， 徐波

(郑州大学 水利与环境学院，河南 郑州 450001)



北京市降雨量与参考作物腾发量多时间尺度的集对分析

张金萍， 林小敏， 徐波

(郑州大学 水利与环境学院，河南 郑州 450001)

为了揭示北京市降雨量和参考作物腾发量之间的不确定性关系，以期为二者的变化规律分析、预报和预测提供支撑，利用1961—2009年的长时间序列资料，应用小波分析方法对北京市的降雨量和参考作物腾发量的波动周期和局部特征进行分析，应用集对分析方法分析不同时间尺度下的降雨量和参考作物腾发量之间的同一性、差异性和对立性。结果表明，北京市降雨量和参考作物腾发量之间存在不同时间尺度的周期波动，且差异性在短、中、长周期尺度水平上占据主要位置，而在中长周期尺度水平上对立性占据主要位置，这为分析降雨量和参考作物腾发量在多时间尺度上的变化规律和二者在多层次上的关系提供支持。

降雨量；参考作物腾发量；小波分析；集对分析；多时间尺度

1　研究背景与意义

降雨量和参考作物腾发量(ET0)的演变特征与匹配程度直接影响着灌区灌溉规划的制定和农业水资源的供需调配，受气象条件、下垫面等因素的影响，二者自身演变规律及其相关关系存在着较强的随机性和不确定性。降雨量和参考作物腾发量的不确定关系反映了需水和用水的模糊性。因此，基于灌区降雨量和参考作物腾发量之间具有的天然相关性，解析降雨量与参考作物腾发量间的不确定性关系，对于指导灌区农业抗旱、调整并优化灌区农业种植结构、保证粮食生产安全等有重要作用。

目前，在关于降雨量与参考作物腾发量的关系研究中，比较普遍的是阐释降雨量与参考作物腾发量的年际、年内变化以及两者之间的简单相关关系[1-5]。但在分析降雨量与参考作物腾发量的关系时，简单的相关关系无法反映二者之间的真实相关关系以及在不同时间尺度上的联系。近年来，以小波分析为代表的多时间尺度分析方法使得揭示水文变量的不确定性成为可能。如冯平等运用集对分析方法，深入分析了汾河与沁河年径流量变化关系的同、异、反特性[6]；张金萍等以泾河张家山水文站为例，对不同时间尺度下的泾河年径流量与其IMF分量之间的同一性、差异性和对立性进行了分析[7]。但这些研究主要集中于对河川径流的不确定性分析，而针对灌区水资源供需匹配的不确定性研究相对较少。本文以北京市为例，运用小波分析方法对1961—2009年的降雨量和参考作物腾发量进行多时间尺度分解，并采用集对分析方法分析不同时间尺度下的降雨量和参考作物腾发量之间的同一性、差异性和对立性，由此为北京地区灌区的灌溉规划和农业发展规划提供参考。

2　主要研究方法

2.1小波分析法

小波变换是时间(空间)频率的局部化分析，通过伸缩、平移运算对信号(函数)逐步进行多尺度细化[8]。小波分析在时频上能够很好地反映随机序列的波动性，较为常用，且简单实用[8]。基于此，应用小波分析方法研究降雨量和参考作物腾发量在多时间尺度上的随机波动性。其基本原理[9]如下：

小波分析主要讨论平方可积函数f(t)。L2(R)为R上平方可积函数构成的函数空间，即

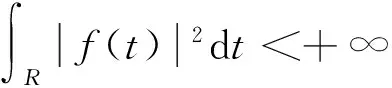
(1)

如果ψ(t)∈L2(R)，且ψ为一个基小波，对基小波进行伸缩和平移变换得到一个小波序列：

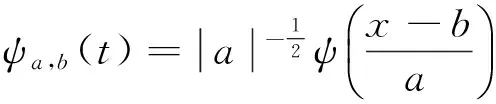
(2)式中:a为伸缩因子;b为平移因子;a，b∈R，且a≠0。

关于基小波ψ的连续小波变换(CWT)为

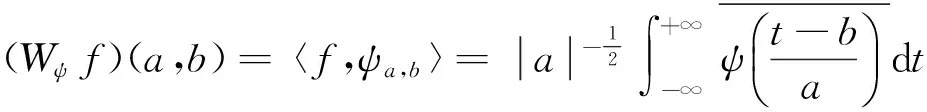
(3)

小波变换将原来的一维信号变换为二维信号，用以分析信号的时频特性。而进行式(4)中关于基小波ψ的小波逆变换，可将二维信号重构回原来的一维信号。

(4)

通过调整伸缩因子a和平移因子b,可得具有不同时频宽度的小波以匹配原始信号的任意位置，用以对信号的时频局部化进行分析。通过离散CWT中的a和b，经离散小波变换(DWT)得离散小波，

(5)

相应的离散的小波变换为:

(6)

对信号进行离散小波变换，信号的基本信息不会丢失。选用具有正交性的小波函数，能够消除小波空间中两点之间因冗余度造成的关联。式(6)的计算误差更小，变换结果的时频函数性质更能反映信号特征。

2.2集对分析法

集对分析的核心思想[10-11]是先将不确定性系统中有关联的两个集合构成集对，再对集对、特定属性做同一性、差异性、对立性分析，然后用联系度描述集对的同、异、反关系，表征不确定性系统中集合A和B多层次上的关系。联系度计算式为：

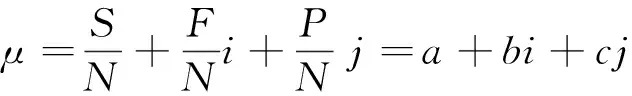
(7)式中：μ为集合A和B的联系度；S为同一性的个数；F为差异性的个数；P为对立性的个数；N为集合特性的总数；S+F+P=N；i为差异不确定系数，取值范围为[-1，1]；j为对立系数，一般情况下取值为-1；a=S/N，为同一度，表示集合A和B就某种属性而言具有相同性质的程度；b=F/N，为差异度，表示集合A和B就某种属性而言具有既不相同又不相反(成为差异性)的程度；c=P/N，为对立度，表示集合A和B就某种属性而言具有相反性质的程度；a、b、c非负且满足归一化条件，即a+b+c=1。

集对分析的一般计算步骤为：依据研究对象的性质，合理构造集合A、B和集对H(A,B)；根据集合A、B的变化特性，制定分类标准，将集合A和B的各个元素进行符号量化处理；将集合A和B的符号量化值两两比较，计算同一性、差异性和对立性的个数；选取合适的i值，计算同一度a、差异度b和对立度c及联系度μ。

3　实际应用

以北京市为例进行说明。所用数据(源自中国科学数据共享网)为北京气象站1961年1月1日—2009年12月31日的逐日气象数据，具体包括降雨量、平均风速、最高气温、最低气温、平均相对湿度、日照时数等，该气象站所处位置为北纬39.8°，海拔高度为31.3 m。其中参考作物腾发量由1998年联合国粮农组织推荐的Penman-Monteith公式计算得到。图1为北京市气象站1961—2009年的降雨量和参考作物腾发量的变化曲线。

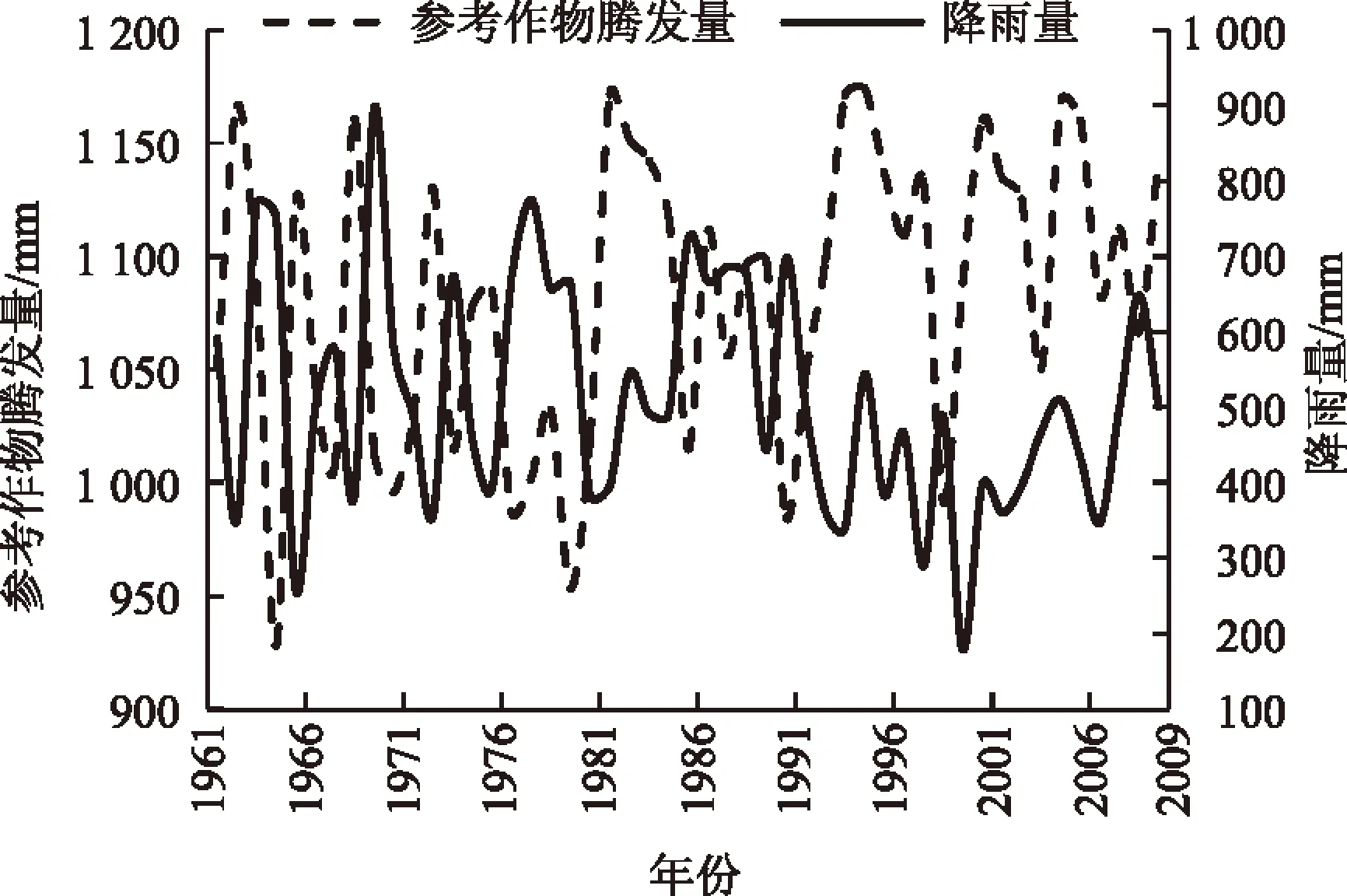
图1　　　　北京市1961—2009年降雨量和参考

3.1北京市降雨量和参考作物腾发量的波动周期分析

运用小波分析方法对年降雨量和参考作物腾发量序列进行多时间尺度分析时，选用紧支集正交小波——Daubechies小波6(简称db6)对数据序列进行一维离散小波分析。通过对年降雨量和参考作物腾发量序列进行多时间尺度小波分解，得到图2和图3所示的逼近成分与细节成分，进而对北京市年降雨量与参考作物腾发量进行多时间尺度下的周期分析。

图2中(a)(b)(c)(d)(e)(f)为进行小波分解得到的信号序列，分别表示北京市年降雨量细节成分序列Pd1、Pd2、Pd3、Pd4、Pd5和逼近成分序列Pa5。

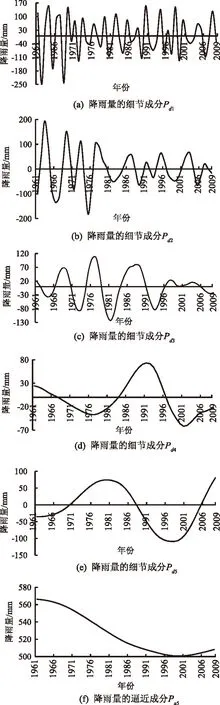
图2　　　　db6小波4尺度分解年降雨量的

图3中(a)(b)(c)(d)(e)为进行小波分解得到的信号序列，分别表示北京市年参考作物腾发量的细节成分序列ET0d1、ET0d2、ET0d3、ET0d4和逼近成分序列ET0a4。图中曲线反映了北京市年降雨量和参考作物腾发量变化的复杂性。

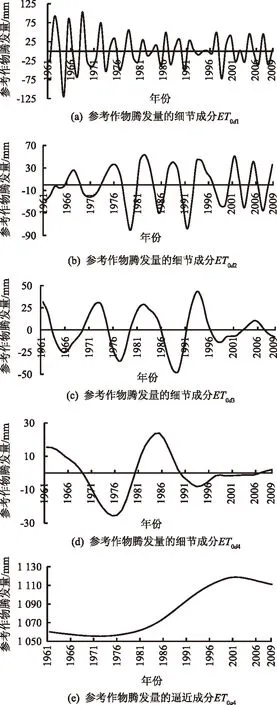
图3　　　　db6小波4尺度分解年参考作物腾发量的

从图2—3中可以看出：

1)北京市降雨量的细节成分序列Pd1具有准2～3 a波动周期，20世纪60年代波动幅度一直较大，70年代至今，波动幅度不大，较为平稳；参考作物腾发量的细节成分序列ET0d1具有准2～4 a波动周期，波动幅度在20世纪60年代中期较大，其余时段波动幅度较为平稳。

2)北京市降雨量的细节成分序列Pd2具有准4～7 a波动周期，20世纪60年代至70年代中期，波动幅度整体较大，但70年代初略有减小，80年代至今波动幅度较为平稳，波动较小；参考作物腾发量的细节成分序列ET0d2具有准6～9 a波动周期，20世纪60年代初至70年代末期，波动幅度逐渐增大，80年代至90年代初期，波动幅度较大，且较为平稳，90年代中期至今，波动幅度有所减小，保持平稳。

3)北京市降雨量的细节成分序列Pd3具有准8～12 a波动周期，波动幅度自20世纪60年代初至70年代末逐渐增大，80年代后，波动幅度逐渐衰减；参考作物腾发量的细节成分序列ET0d3具有准10～12 a波动周期，波动幅度变化缓慢，60年代初至80年代初期呈平稳趋势，80年代中期至90年代中期，波动幅度突然增大，90年代后期至今波动幅度有较大衰减。

4)北京市降雨量的细节成分序列Pd4具有准24 a波动周期；参考作物腾发量的细节成分序列ET0d4具有准18 a波动周期，20世纪60年代初至80年代中期波动幅度较大，80年代末期至今，波动幅度较小，呈现逐渐衰减的趋势。

5)北京市降雨量的细节成分序列Pd5具有准36 a波动周期。

6)北京市年降雨量的逼近成分序列Pa5反映出其在整个时段内呈现逐渐减小的态势；参考作物腾发量的逼近成分序列ET0a4反映出其在整个时段内存在逐渐增加的态势。

通过利用SPSS软件对年降雨量序列进行因子分析，结果表明:Pd1、Pd2、Pd3、Pd4、Pd5、Pa5的方差贡献率分别为22.875%、17.422%、17.022%、16.518%、15.958%、10.206%;Pd1、Pd2、Pd3、Pd4、Pd5、Pa5的累计方差贡献率分别为22.875%、40.297%、57.319%、73.836%、89.794%、100.000%;表明年降雨量的Pd1、Pd2、Pd3、Pd4序列在年降雨量波动过程中占主导位置。

3.2降雨量与参考作物腾发量变化的多时间尺度集对分析

将降雨量的各分量与参考作物腾发量各分量分别进行多时间尺度集对分析。Pd1、Pd2、Pd3、Pd4分别表示北京市降雨量的细节成分序列d1、d2、d3、d4。ET0d1、ET0d2、ET0d3、ET0d4分别表示北京市参考作物腾发量的细节成分序列d1、d2、d3、d4。设定2～4 a为短周期，5～8 a为中周期，9～12 a为中长周期，18～24 a为长周期。将序列Pd1记为集合A1，序列Pd2记为集合A2，序列Pd3记为集合A3，序列Pd4记为集合A4，序列ET0d1记为集合B1，序列ET0d2记为集合B2，序列ET0d3记为集合B3，序列ET0d4记为集合B4，其中样本容量n=49。如此将构成4个集对，即H(A1,B1)、H(A2,B2)、H(A3,B3)、H(A4,B4)。采用均值标准差法将序列Pd1、Pd2、Pd3、Pd4、ET0d1、ET0d2、ET0d3、ET0d4分为枯(Ⅰ)、平(Ⅱ)、丰(Ⅲ)3个等级，对应的区间分别为(-∞，X-0.5δ)、[X-0.5δ，X+0.5δ)、[X+0.5δ，+∞)。X和δ分别为集合的均值和标准差。评价分类计算结果见表1和表2。

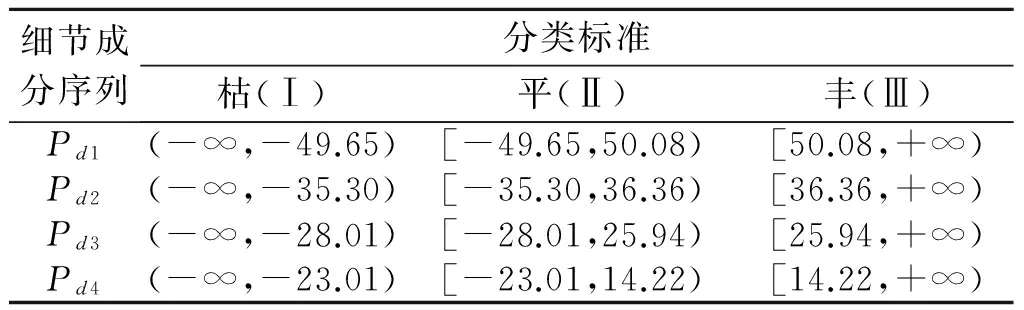
表1　降雨量评价分类标准　mm

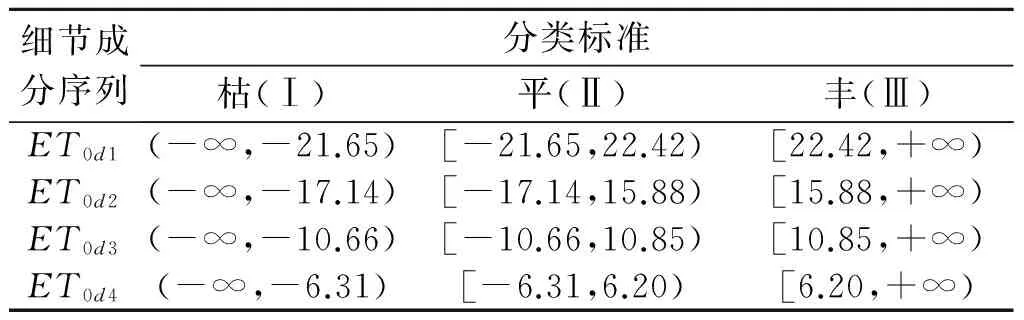
表2　参考作物腾发量评价分类标准　mm

根据表1、表2，可对各集对的元素进行符号量化处理，取i=0.5，j=-1，统计计算其同一度a、差异度b和对立度c以及联系度μ值，结果见表3。

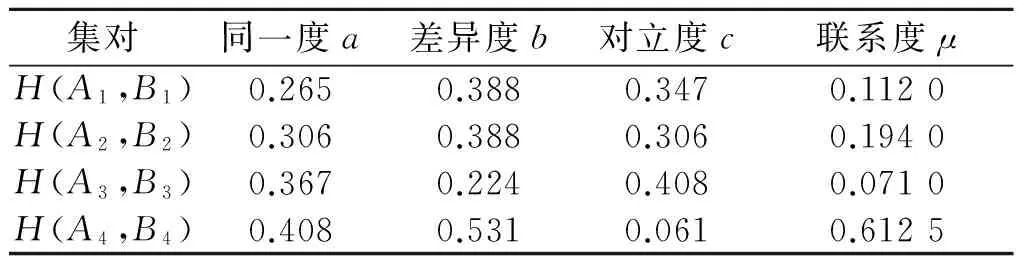
表3　降雨量与参考作物腾发量多时间尺度集对分析

由表3可知：①北京市年降雨量的细节成分序列Pd1与年参考作物腾发量的细节成分序列ET0d1，对应波动短周期，不确定性关系中差异度最大，为0.388。北京市年降雨量的细节成分序列Pd2与年参考作物腾发量的细节成分序列ET0d2，对应波动中周期，不确定性关系中差异度最大，为0.388。北京市年降雨量的细节成分序列Pd3与年参考作物腾发量的细节成分序列ET0d3，对应波动中长周期，不确定性关系中对立度最大，为0.408。北京市年降雨量的细节成分序列Pd4与年参考作物腾发量的细节成分序列ET0d4，对应波动长周期，不确定性关系中差异度最大，为0.531。②同一度随波动周期的变化，与长周期对应的同一度最大，为0.408，说明降雨量和参考作物腾发量的同一度主要表现在长周期尺度水平上。③差异度随波动周期的变化，与长周期对应的差异度最大，为0.531，说明降雨量和参考作物腾发量的差异度主要表现在长周期尺度水平上。④对立度随波动周期的变化，与中长周期对应的对立度最大，为0.408，说明降雨量和参考作物腾发量的对立度主要表现在中长周期尺度水平上。⑤联系度值随波动周期的变化，与中长周期对应的联系度最小，这与在该尺度水平上的对立度最大、差异度最小是一致的；与长周期对应的联系度最大，这与在该尺度水平上的差异度最大、对立度最小是一致的。⑥北京市年降雨量与年参考作物腾发量的变化，在短、中、长周期以差异性为主，在中长周期以对立性为主；在短周期对立度较同一度仍占主要位置，而在长周期同一度较对立度占主要位置。

4　结语

运用多种方法，对北京市降雨量和参考作物腾发量的演变规律以及二者之间的关系进行了分析，得出如下结论：

1)北京市年降雨量具有准2～3、4～7、8～12、24、36 a的波动周期，年参考作物腾发量具有准2～4、6～9、10～12、18 a的波动周期。这反映了北京市年降雨量与参考作物腾发量变化的复杂性，可为进一步分析其在多时间尺度下的变化规律与揭示二者在多层次上的关系提供基础。

2)北京市年降雨量与参考作物腾发量之间具有复杂的不确定性关系，这种不确定性联系在短、中、长周期以差异性为主，在中长周期以对立性为主，表明在短、中长周期二者趋于相反的可能性较大。这反映了在相当长一段时间内北京市年降雨量与参考作物腾发量在不同时间尺度上大致呈相反的变化趋势，可为灌区合理制定灌溉规划、科学调配水资源、有效指导农业抗旱等提供理论支持。

[1]宋振伟,唐衡,孔箐锌，等．京郊平原参考作物腾发量及其与气象因子相关性研究[J]．灌溉排水学报，2009，28(6)：74-77．

[2]田俊武,尚松浩,孙丽艳，等．山西潇河灌区参考作物腾发量和降水的随机特性[J]．农业工程学报，2005，21(10)：26-30．

[3]张山清,普宗朝,宋良娈，等．吐鲁番地区气候变化对参考作物蒸散量的影响[J]．中国农业气象，2009，30(4)：532-537．

[4]刘增进,何军,陈浩荣，等．豫东平原参考作物腾发量时空变化分析及影响研究[J]．中国农村水利水电，2008(9)：65-68．

[5]李宝萍,杜明侠,何军．郑州地区各气象要素与参考作物腾发量的相关性研究[J]．河南农业大学学报，2007，41(4)：391-395．

[6]冯平,韩瑞光,丁志宏．河流之间径流关系不确定性的多时间尺度SPA研究[J]．应用基础与工程科学学报，2009，17(5)：16-25．

[7]张金萍,丁志宏．基于集对分析的泾河河川径流多时间尺度变化研究[J]．干旱区资源与环境，2014，28(5)：176-179．

[8]马建琴,韩曦．甘肃省近48年春旱时空变化趋势分析[J]．华北水利水电学院学报，2013，34(3)：40-43．

[9]张德丰．MATLAB小波分析[M]．北京：机械工业出版社，2009：53-55．

[10]王文圣,李跃清,金菊良，等．水文水资源集对分析[M]．北京：科学出版社，2010：13-16．

[11]杜海艳,黄奕辉．基于集对分析的购房决策模型优化[J]．华北水利水电学院学报，2012，33(2)：148-150．

Set Pair Analysis on Rainfall and Reference Crop Evapotranspiration of Beijing City in Multiple Time-scales

ZHANG Jinping, LIN Xiaomin, XU Bo

(School of Water Conservancy & Environment, Zhengzhou University, Zhengzhou 450001, China)

For revealing the uncertainty between rainfall and reference crop evapotranspiration (ET0) , which can provide support for the analysis on their change laws and forecast, based on the data series of rainfall andET0in Beijing City from 1961 to 2009，the local characteristics and fluctuation periods of rainfall andET0were analyzed with the wavelet analysis method, and the identity, discrepancy and contrary of rainfall andET0under multi-time scales were revealed using the set pair analysis. The results show that there are complex periodic fluctuation with multi-time scales between rainfall andET0, and the discrepancy is reflected in all the periodic scales while the contrary is mainly presented in the middle and long periodic scales. It can provide technological support for the analysis of change laws and relationship between rainfall andET0in multi-time scales.

rainfall; reference crop evapotranspiration; wavelet analysis; set pair analysis; multi-time scales

2016-04-30

国家自然科学基金项目(51309202)；河南省高校科技创新团队支持计划项目(13IRTSHN030)。

张金萍(1979—)，女，河南沁阳人，讲师，博士，主要从事节水与水资源高效利用、广义水资源合理配置与区域水循环等方面的研究。E-mail:jinping2000_zh@163.com。

TV122

A

1002-5634(2016)04-0054-05

(责任编辑：杜明侠)

DOI:10.3969/j.issn.1002-5634.2016.04.009