交通拥堵的平均场延迟反馈控制方法*
郭 言,薛 郁**,施 映,李瑞鑫,何红弟
(1.广西大学物理科学与工程技术学院,广西南宁 530004;2.上海海事大学物流研究中心和上海航运物流信息工程研究中心,上海 200135)
交通拥堵的平均场延迟反馈控制方法*
郭言1,薛郁1**,施映1,李瑞鑫1,何红弟2
(1.广西大学物理科学与工程技术学院,广西南宁530004;2.上海海事大学物流研究中心和上海航运物流信息工程研究中心,上海200135)
【目的】在优化速度模型的基础上,引入平均场延迟反馈控制方法抑制交通的拥堵。【方法】将当前车受到的所有其它车的作用用一个平均场力来代替,将延迟耦合作为延迟反馈控制项,在交通流演化过程中,通过开-关(on-off)加载控制以抑制交通的拥堵;通过线性稳定性分析得出稳定性条件;最后用数值模拟验证控制方法的有效性。【结果】稳定性分析得出交通流在控制作用下趋于稳定,数值模拟分析对比发现拥堵交通流在施加控制后,车间距-速度相图中的交通滞后曲线区域缩小,以此判断交通拥堵得以缓解。【结论】交通流平均场延迟反馈控制方法可以有效地抑制交通拥堵,控制增益越大,交通拥堵缓解程度越好,而且该反馈控制在智能交通(ITS)中易于实现。
优化速度模型平均场理论延迟反馈控制方案稳定性条件数值模拟交通滞后
0 引言
【研究意义】随着社会经济的发展、城市化进程的加快,交通干线不断拓展,汽车数量年年递增,所引发的交通拥堵也日趋严重,而且拥堵时的车辆排放给环境带来严重污染。交通拥堵问题早在1933年就引起有关学者的重视和研究。在交通过程中会出现畅行、时停时走、宽运动堵塞等交通现象,而且这些交通现象显现出分形、长程关联、自相似性等特性。【前人研究进展】为解决交通拥堵问题,近年来人们提出许多交通流模型,例如宏观的流体力学模型,介观的动理学模型以及微观的跟驰模型和元胞自动机模型等[1-3]。经典的交通流跟驰模型有优化速度模型[4]、广义力模型[5]和耦合映像模型[6-8]等等。在这些模型当中,优化速度模型被广泛地应用于交通拥堵,并且能够解释交通流动力学演化过程中交通拥堵的形成;耦合映像模型为优化速度模型的离散形式。1999年Konishi等[6]在耦合映像模型上提出延迟反馈控制方法,在开放边界瓶颈的噪声作用下,交通系统在该控制方法下能够较好地运行;2011年Ge等[9]提出改进的优化速度模型,该模型涉及到当前车辆与前车的车间距离;2013年Zhou等[10]使用耦合映像模型的延迟反馈控制方法研究其对交通系统的控制作用,结果表明该方法对交通过程中出现的聚集堵塞有较好的抑制作用。因此,在优化速度模型或耦合映像模型上采用的控制方法能够有效地抑制交通拥堵[11-12]。在最近几年,反馈控制方法也被广泛应用于交通流宏观模型[13-17]:2015年Ge等[13]在格子流体力学模型中提出反馈控制方法,该方法应用t时刻第j格子和第j+1格子的流量差作为反馈控制信号来控制交通流拥堵;Redhu等[14]应用下游的第j+1格子的t时刻和t-τ时刻的流量差作为控制交通拥堵的延迟反馈控制策略。【本研究切入点】智能交通系统可在整体上掌握道路交通信息,监控整条道路上车辆的相互作用。随着智能交通系统的快速发展,有必要从整体上对交通拥堵进行控制,而在非线性网络系统的控制中,网络中的节点相互作用往往引入平均场耦合理论进行反馈控制。类似地,本研究在交通系统中相互作用的车辆引进平均场耦合理论来研究交通拥堵问题。【拟解决的关键问题】基于平均场理论的思想,利用智能交通系统所提供的整条道路交通信息,如道路中每一车辆的位置、速度和时间等,对整个系统进行有效信息的提取,从而引入平均场延迟反馈控制策略进行交通控制,达到抑制交通拥堵的目的。
1 平均场延迟反馈控制模型
Bando等[18-21]提出优化速度模型:
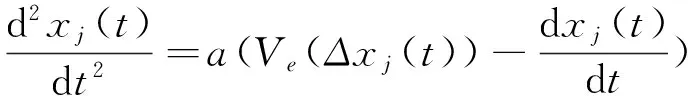
(1)
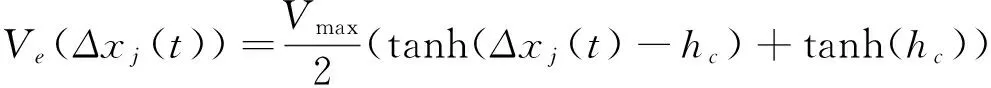
其中Vmax表示最大速度,hc表示车辆之间的安全距离。Bando等[18-21]证明优化速度模型的稳定性条件为

(2)

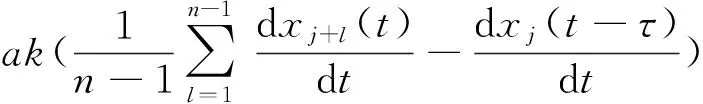
(3)
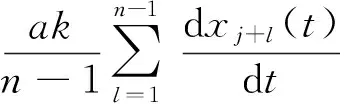
2 稳定性条件的线性分析
为研究交通流中平均场延迟反馈控制的效果,我们对平均场延迟反馈控制方案进行线性稳定性分析。首先,交通系统处于稳定状态,在周期边界条件下,车辆均匀地分布在道路上。因此交通系统中车辆的空间位置、车间距离和行车速度表示如下:
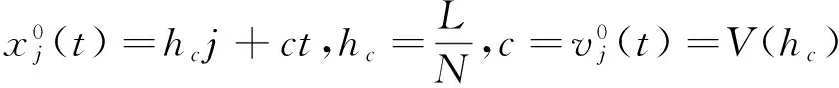
其中c表示稳定态下车辆的速度,hc表示两辆车之间平均距离,L表示道路的长度,N表示道路上的车辆数量。当系统中的车辆处于稳定状态时,车辆匀速行驶,但是车辆常常受到驾驶员、环境等不确定因素的作用。在t时刻处于稳态的第 j辆车空间位置受到一个微扰动yj(yj≪1)作用(该微扰将沿车流传播),则第 j辆车在该微扰作用下的位置为

(4)
将方程(4)代入到方程(3),得到化简的微扰方程为

(5)
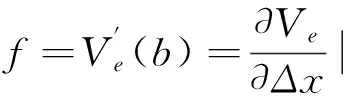
y(j,t)=exp(iαkj+zt)。
(6)
将方程(6)代入到方程(5)得

(7)
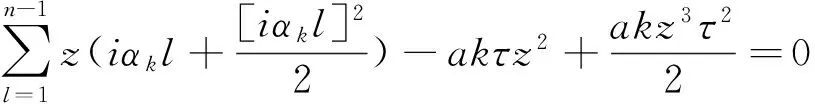
(8)
方程(8)中含有一阶项iαk和二阶项(iαk)2,将z展开为z=z1(iαk)+z2(iαk)2+…,代入方程(8)中得

(9)
从方程(9)中可以得到z1和z2所满足的等式:
z1=f,
(10)
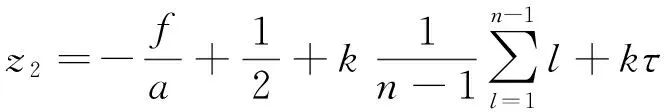
(11)
从微扰yj和z可以知道,当z2<0时,微扰作用下的均匀流随时间演化将呈现不稳定的状态;当z2>0时,系统将处于稳定的状态,于是可以得出如下的稳定性条件:

(12)
用敏感系数表示为

(13)
车流稳定性与3个因素有关,分别是延迟反馈增益、车间距和系统的总车辆数。在另外2个因素已经确定的情况下,延迟反馈增益在车流稳定性方面起重要作用,驾驶员的敏感系数随着延迟反馈增益增大而减小。
3 数值模拟
如图1所示,在交通系统中对序号为2,30,50和100的4辆汽车进行连续跟踪,并且在不同的延迟反馈增益k=0,0.3,0.5,0.7下对行进过程中的4辆车进行每时步的车速检测,根据所得到车速变化可以确定延迟反馈控制的效果。从图1a中可以看到,没有控制时车辆在演化不久就变得不稳定,在250 s时速度变化幅度很大。这是在微扰的作用下,微扰的传播和增强使得车流处于不稳定状态所导致的结果。在系统演化到300 s时,将平均场延迟反馈控制加入到不稳定的交通系统中,在不同的延迟反馈增益的作用下,不同车辆速度幅度变化逐渐衰减,直至稳定状态(图1b~d);另外,随着延迟反馈增益的增大,系统在相同时间的演化中更快地趋于稳定状态,平均场延迟反馈控制效果越明显(图1c~d)。
图2显示从0~1 000 s的时间内在不同延迟反馈增益时所有车辆的位置、速度和时间的速度时空演化图。速度时空演化图可以整体显示各时刻处于不同位置的车辆速度变化情况,在速度较高区域表示该时刻所对应车辆以高速行驶;相反地,速度较低区域则表示该区域车辆处于交通拥堵。在不同延迟反馈控制作用下,车辆速度变化很快地趋于速度为v=1 m/s的稳态(图2b~d),达到控制交通拥堵的目的,这表明平均场延迟反馈控制具有较高的效率。

图1不同延迟反馈增益的车辆速度变化
Fig.1Temporal velocity change with the time as k=0, 0.3, 0.5, 0.7

图2车辆速度的时空演化
Fig.2Space-time evolution of velocity
从图3a中可以看到,在没有控制的交通系统,不同车辆的速度变化很大,交通处于拥堵状态。在不同的反馈增益k作用下(图3b~d),交通拥堵消失,系统处于速度v=1 m/s的稳定状态,表明平均场延迟反馈控制方案具有一定可行性。
为进一步了解交通系统中车辆在行驶过程中的微观行为,我们绘制车辆位置-时间(xn,t)的时空斑图。当交通系统没有受到控制时(图4a),在周期边界条件下,微扰作用使得车辆在行驶过程中出现车辆积聚在一起的区域——交通阻塞,并且这种交通阻塞不会消失而是向上游传播, 随着时间的增加,这些交通阻塞会汇合在一起形成更大的交通阻塞区域,最后形成较大的交通阻塞带, 这就是时停时走的交通现象。出现交通阻塞后在300 s时加入平均场延迟反馈控制,交通阻塞区域逐渐消失,车辆逐渐扩散:在较小延迟反馈增益k=0.3时,交通阻塞区域消散较小,还存在不明显向后传播的阻塞带(图4b);在延迟反馈增益k较大时,交通阻塞带消失,车辆呈现均匀分布,延迟反馈增益k越大,平均场延迟反馈控制的控制效果就越明显(图4c~d)。

图3终态车辆的速度轮廓图
Fig.3Velocity profile of all vehicles

图4不同反馈增益下车辆位置-时间(xn,t)的时空斑图
Fig.4Plots of the spatiotemporal patterns (xn,t) of all vehicles on the cycle road for different control gain k
为了解控制作用下的车流状态变化,我们在车间距-速度的相图中确定所有车辆的状态变化。在没有施加控制时,出现较大区域的交通滞后回线,车辆间距小,车辆较为密集出现,可以判断交通系统出现低速拥堵(图5)。相较于时空斑图(图4a),在时间段为0~300 s时,相图中出现许多密集较小的阻塞带(图5a);在时间段301~500 s和501~1 000 s时,相图中间部分积聚消失,积聚部分分布在交通滞后曲线的边缘处(图5b~c),对照图4a交通系统中车辆演化较长时间的时空斑图,由于微扰的作用,车辆在演化一段时间后将慢慢发生堵塞积聚形成密集而细小的阻塞带,而且随着时间延长,较小的阻塞带逐渐合并在一起形成较大的阻塞带,即形成了在不稳定状态下时停时走的交通现象。

图5k=0时不同时间段所有车辆的车间距-速度(Δx,v)相图
Fig.5 Phase space of all vehicles for k=0 at different times
在延迟反馈控制增益k=0.3,0.5,0.7情况下,于300 s时加入平均场延迟反馈控制后,可以看到相图的交通滞后曲线的区域明显地缩小(图6);在长时间后,交通滞后曲线收缩成一条曲线(图7),随着控制增益增大,交通滞后曲线就越明显地收缩成一条曲线(图6,图7),表明平均场延迟反馈控制作用使得交通拥堵得到有效缓解,达到控制的目的。

图6301~500 s时所有车辆的车间距-速度(Δx,v)相图
Fig.6Phase space of all vehicles within the time from 301 to 500 s

图7501~1 000 s时所有车辆的车间距-速度(Δx,v)相图
Fig.7Phase space of all vehicles within the time from 501 s to 1 000 s
4 总结
本研究在优化速度模型的基础上,提出平均场延迟反馈控制方法抑制交通的拥堵。本研究将当前车所受到所有其它车的作用用一个平均场力来代替,通过延迟耦合作为延迟反馈控制项,在交通流演化过程中,通过开-关(on-off)加载控制以抑制交通的拥堵。通过线性稳定性分析方法,得出稳定性条件,稳定性分析表明交通流在控制作用下趋于稳定。数值模拟验证控制方法的有效性,从数值模拟得出的车辆速度时空图、车辆位置-时间(xn,t)的时空斑图和控制后车间距-速度相图中交通滞后曲线区域缩小的分析可知,平均场延迟反馈控制可以有效地抑制交通拥堵,控制增益越大,交通拥堵缓解程度越好,抑制交通拥堵的效果就越好,达到交通控制的目标,而且这样的平均场延迟反馈控制在智能交通(ITS)中易于实现。
[1]CHOWDHURY D,SANTEN L,SCHADSCHNEIDER A.Statistical physics of vehicular traffic and some related systems[J].Phys Rep,2000,329:199-329.
[2]HELBING D.Traffic and related self-driven many-particle systems[J].Rev Mod Phys,2001,73:1067-1141.
[3]KERNER B S.The Physics of Traffic[M].Berlin:Springer,2004.
[4]HELBING D,TILCH B.Generalized force model of traffic dynamics[J].Phys Rev E,1998,58:133-138.
[5]KONISHI K,KOKAME H,HIRATA K.Coupled map car-following model and its delayed-feedback control[J].Phys Rev E,1999,60:4000-4007.
[6]KONISHI K,KOKAME H,HIRATA K.Delayed-feedback control of spatial bifurcations and chaos in open-flow models[J].Phys Rev E,2000,62:384-388.
[7]ZHAO X M,GAO Z Y.A control method for congested traffic induced by bottlenecks in the coupled map car-following model[J].Physica A:Statistical Mechanics and Its Applications,2006,366:513-522.
[8]HAN X L,JIANG C Y,GE H X,et al.A modified coupled map car-following model based on application of intelligent transportation system and control of traffic congestion[J].Acta Phys Sin,2007,56:4383-4392.
[9]GE H X,CHENG R J,LI Z P.Considering two-velocity difference effect for coupled map car-following model[J].Acta Phys Sin,2011,60:080508(1)-080508(9).
[10]ZHOU T,SUN D H,ZHAO M,et al.Feedback control scheme of traffic jams based on the coupled map car-following model[J].Chin Phys B,2013,22(9):090205.
[11]JIN Y F,HU H Y.Stabilization of traffic flow in optimal velocity model via delayed-feedback control[J].Cummun Nonlinear Sci Numer Simulat,2013,18:1027-1034.
[12]ZHENG Y Z,ZHENG P J,GE H X.An improved car-following model with consideration of the lateral effect and its feedback control research[J].Chin Phys B,2014,23(2):020503.
[13]GE H X,CUI Y,ZHU K Q,et al.The control method for the lattice hydrodynamic model[J].Commun Nonlinear Sci Numer Simulat,2015,22(1/2/3):903-908.
[14]REDHU P,GUPTA A K.Delayed-feedback control in a lattice hydrodynamic model[J].Commun Nonlinear Sci Numer Simulat,2015,27:263-270.
[15]YU S W,SHI Z K.The effects of vehicular gap changes with memory on traffic flow in cooperative adaptive cruise control strategy[J].Physica A,2015,428:206-223.
[16]DAVIS L C.Modifications of the optimal velocity traffic model to include delay due to driver reaction time[J].Physica A,2003,319:557-567.
[17]GE H X,DAI S Q,DONG L Y,et al.Stabilization effect of traffic flow in an extended car following model based on intelligent transportation system application[J].Physical Review E,2004,70:066134.
[18]BANDO M,HASEBE K,NAKAYAMA A,et al.Dynamical model of traffic congestion and numerical simulation[J].Phys Rev E,1995,51(2):1035-1042.
[19]BANDO M,HASEBE K,NAKAYAMA A,et al.Structure stability of congestion in traffic dynamics[J].Japan J Indust Appl Math,1994,11:203-223.
[20]BANDO M,HASEBE K,NAKANISHI K,et al.Analysis of optimal velocity model with explicit delay[J].Phys Rev E,1998,58:5429-5435.
[21]BANDO M,HASEBE K,NAKANISHI K,et al.Delay of vehicle motion in traffic dynamics[J].Japan J Indust Appl Math,2000,17:275-294.
(责任编辑:米慧芝)
Mean-field Delay-feedback Control Scheme for Traffic Jam
GUO Yan1,XUE Yu1,SHI Ying1,LI Ruixin1,HE Hongdi2
(1.College of Physical Science and Engineering,Guangxi University,Nanning,Guangxi,530004,China;2.Logistics Research Center & Shanghai Engineering Research Center of Shipping Logistics Information,Shanghai Maritime University,Shanghai,200135,China)
【Objective】A mean-field delay-feedback control scheme for traffic jam is proposed based on the optimal-velocity (OV) model,in order to suppress traffic jam.【Methods】The interaction among other vehicles can be taken the place of an average force exerting on each vehicle as delay-feedback control term by delayed coupling.The stability condition is derived from OV equation with a feedback control term by linear stability analysis.The effectiveness of the mean-field feedback control scheme are verified by simulation.【Results】The stability condition indicates that traffic flow approaches to steady state under control.The numerical simulation shows the region of traffic hysteresis curves in phase space(headway vs velocity) is shrunken,which indicates traffic jam is reduced under control.【Conclusion】The mean-field delay-feedback control scheme of traffic flow can effectively suppress traffic jam.The stronger the control gain is, the less the traffic jam is.And the mean-field delay-feedback control scheme is easily realized in Intelligent Traffic System(ITS).
optimal-velocity model,mean-field,delay-feedback control scheme,stability condition,simulation,traffic hysteresis
2016-05-15
2016-06-20
郭言(1990-),男,硕士研究生,主要从事交通控制理论研究。
U491.1+12
A
1005-9164(2016)03-0194-08
*国家自然科学基金项目(11262003),广西自然科学基金项目(20140593)和广西研究生创新项目(YCSZ2012013)资助。
**通讯作者:薛郁(1963-),男,博士生导师,教授,主要从事交通流动力学研究,E-mail:yuxuegxu@gxu.edu.cn。
广西科学Guangxi Sciences 2016,23(3):194~201
网络优先数字出版时间:2016-07-13【DOI】10.13656/j.cnki.gxkx.20160713.002
网络优先数字出版地址:http://www.cnki.net/kcms/detail/45.1206.G3.20160713.0857.004.html

