角接触球轴承接触应力的有限元分析
高恒强,蔡红娟GAO Heng-qiang, CAI Hong-juan(.中国地质大学(武汉)机电学院,武汉 430074;.武昌首义学院 电工电子教学基地,武汉 430064)
角接触球轴承接触应力的有限元分析
高恒强1,蔡红娟2
GAO Heng-qiang1,CAI Hong-juan2
(1.中国地质大学(武汉)机电学院,武汉 430074;2.武昌首义学院 电工电子教学基地,武汉 430064)
推导了基于Hertz接触理论的载荷分布和接触应力的计算公式,并利用有限元分析软件ANSYS,建立了角接触球轴承接触分析的三维有限元模型。对单个滚珠的轴承接触问题进行了有限元分析,得到了径向载荷作用下球轴承的接触应力分布趋势。通过与Hertz理论计算结果对比分析,两者结果比较接近。
角接触球轴承;有限元;接触应力
0 引言
角接触球轴承是机械中承受载荷和传递运动的重要支承零件,它依赖各部件之间的滚动接触来支持旋转零件,是高易损零件[1]。在使用角接触球轴承的机械系统中,很多的机械故障都是由于轴承的失效造成的[2]。因此,对角接触球轴承进行受力分析和运动分析,是十分必要的。轴承接触分析的困难在于滚动体和圈体的接触,随着载荷的增大,点接触变为面接触,其接触面积和接触力大小将会受两接触面间的初始间隙、摩擦系数以及所施加的载荷影响而产生变化,因此接触面大小和边界条件都在不断地变化,属于边界非线性问题[3]。进入二十一世纪以来,伴随着有限元法和边界元法等数值计算方法的不断完善和计算机硬件技术水平的快速提高,为几何非线性的接触问题提供了有力的计算工具,使接触的全过程的计算机数值模拟得到了可能。
本文应用Hertz理论,对滚珠的接触问题进行了分析,建立了相应的有限元模型,对不同载荷下的接触应力进行了计算,并将有限元法分析结果与基于Hertz理论的理论求解结果进行了比较,结果表明本文建立的单一滚珠的有限元简化模型是合理的。
1 角接触球轴承接触理论分析
角接触球轴承磨损仿真的研究首先需要解决的是接触力学的分析问题。传统的接触问题主要用Hertz弹性接触理论来进行分析[4]。
对于给定的球-滚道接触,可由点接触的Hertz理论得到球轴承的点接触时弹性变形量δ与载荷Q的关系:
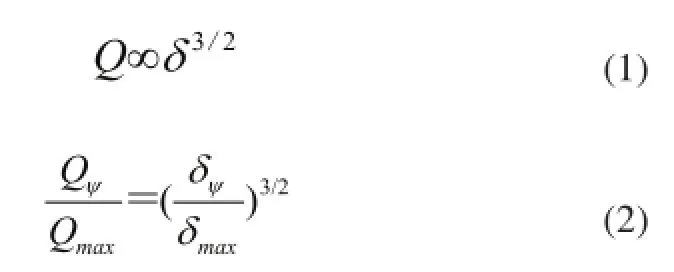
考虑径向游隙的球轴承如图1所示,图中Di和Do分别为内外圈直径。对于刚性支撑的轴承,其承受径向载荷作用时,在任意角度位置的滚动体径向位移[4]可表示为:

式(3)可以按照最大变形量改写为:
当游隙Pd为零时,有
根据式(1),可以得到由径向游隙确定的负荷区域的角度范围为:

由此可知,对于零游隙,最大接触角ψL= 90°。
于是,由式(2)和式(4)得:
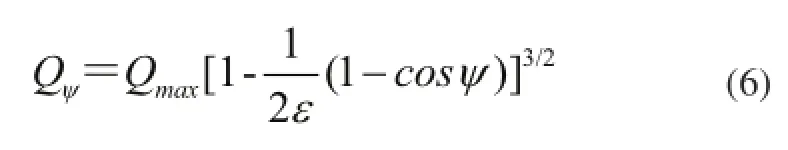
为了满足静力平衡,作用的径向载荷Fr必须等于滚动体载荷的竖向分量之和,即:

将式(6)代入式(7),可得:

对于仅承受径向载荷作用下的球轴承,承受载荷最大的滚动体所承担的载荷为:

式中:Fr为轴承的径向载荷;Z为滚珠数量;α为接触角。
2 角接触球轴承接触应力的有限元分析
2.1有限元模型的建立
为了较好的反映轴承在工作中整体的变形及受力分布情况,本文以型号为7008C的角接触球轴承为例,利用有限元分析软件ANSYS,对其建立接触分析的三维有限元模型,分析其接触应力与载荷分布。7008C的几何参数取值为:轴承外径Do=68mm,轴承内径Di=40mm,外圈滚道直径do=61mm,内圈滚道直径di=46.97mm,外圈滚道沟曲率半径ro=3.78mm,内圈滚道沟曲率半径ri=3.99mm,球直径D=7mm,节圆直径dm=54mm,轴承宽度B=15mm,球数目Z=18,接触角α=15°。
轴承的内、外圈及滚动体的材料均为GCr15轴承钢,相关参数选择为:滚动体及内、外圈的密度ρ= 7.83×103Kg·(m3)-1,弹性模量E=2.07×105MPa,泊松比v = 0.3。
在有限元分析中,接触问题通常采用“试探-校核”的迭代方法进行求解[5],如此则需要较大的计算资源,为了节省计算资源,考虑到轴承的对称性,这里建立了单个滚珠的有限元模型进行分析,如图2所示。采用SOLID185单元建立实体模型,使用MESH200单元划分网格,选取目标单元TARGE170和接触单元CONTA174,建立面面接触模型。整个模型共划分了58752个单元,有60851个节点。
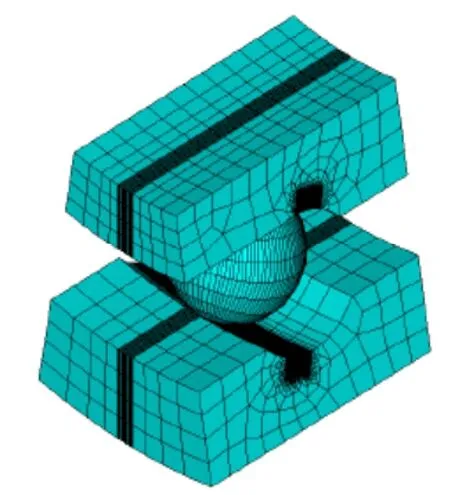
图2 单个滚珠轴承模型
2.2边界条件及约束方式
单滚珠模型所施加的约束条件与完整轴承模型基本一致,即:1)沿-y方向将径向载荷平均施加到内圈内圆面中心线的每个节点上;2)将内圈内圆面上所有节点耦合径向x和轴向y方向的平动自由度;3)约束内外圈背面z方向的位移。如图3所示。

图3 单个滚珠有限元模型及其约束条件和载荷
2.3仿真结果分析
由式(9)可知,当完整轴承的径向载荷为100N时,单个滚珠所承受的最大载荷约为27.78N。则对单滚珠在径向载荷为27.78N时的接触应力进行分析,计算结果如图4所示。从图中可以看出,内外圈的最大接触应力分别为998.4MPa和831.6MPa,与前面得到的完整轴承模型内外圈最大接触应力的理论计算结果误差分别为9.1% 和10.9%。
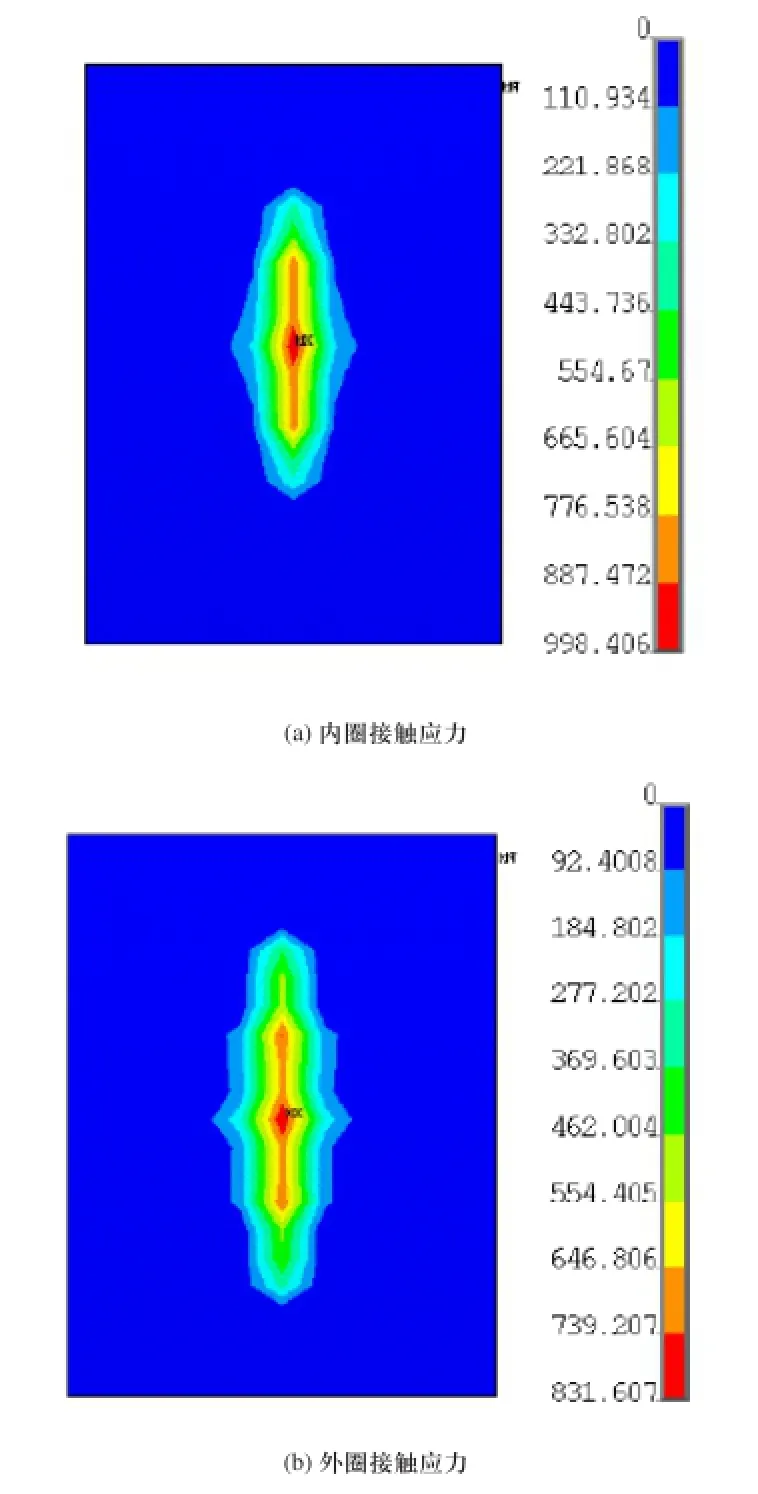
图4 单个滚子有限元模型内外圈最大接触应力
通过前面分析,由式(7)和式(9)可以计算出在轴承径向载荷为100N时,不同位置角的滚珠所承受的载荷。对承受不同载荷的滚珠的内外圈接触应力进行有限元计算,并将计算结果与Hertz接触理论计算结果进行对比,结果如图5所示所示。从图5中可以看出:1)有限元计算结果与Hertz接触理论计算结果误差较小,说明这种单滚珠简化模型是可行的;2)对于承受单一径向载荷的角接触球轴承,位置角为0°的滚珠与内圈的接触应力最大。随着位置角的增大,球与内圈的接触应力先逐渐减小,在接触角为100°~260°时,接触应力为零,然后再逐渐增大;3)球与外圈的接触应力分布具有与内圈同样的规律;4)同一位置角处,球与内圈的接触应力大于与外圈的接触应力。
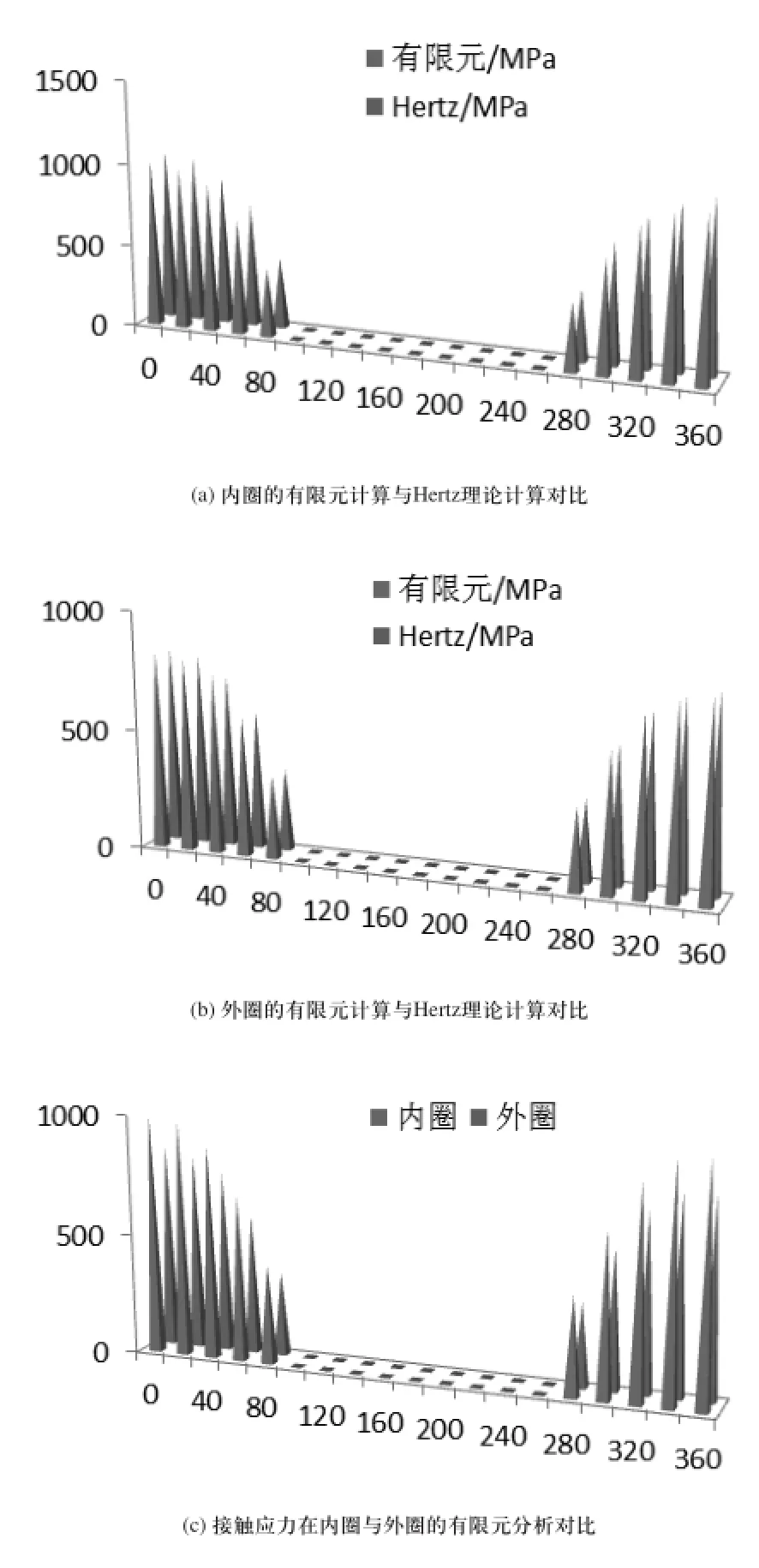
图5 不同位置角滚子的接触应力
【】【】
3 结论
本文应用Hertz弹性理论接触模型,对不同载荷作用下的接触应力进行了推导,并针对角接触球轴承的接触问题建立了相应的有限元模型。对径向载荷作用下的球轴承的载荷分布进行了分析,建立了单一滚珠的有限元简化模型,对不同载荷下的轴承接触应力进行了有限元计算,计算结果符合Hertz理论的计算结果,表明本文建立的单一滚珠的有限元简化模型是合理的。
[1] 刘旺玉,李静.基于Hertz理论的深沟球轴承动态接触分析[J].机械设计与制造.2011,(8):224-226.
[2] 魏延刚,等.角接触球轴承极限推力载荷有限元分析[J].大连交通大学学报.2014,35(10):55-59.
[3] 吴振勇,任成祖,徐强.混合陶瓷球轴承优化设计中接触问题的三维有限元分析[J].机械设计.2004,21(5):47-49.
[4] 吴飞科,等.关于Hertz点接触理论适用范围的探讨[J].轴承.2007,(5):1-3.
[5] 姚建松,李一浩.一种计算深沟球轴承径向刚度的新方法[J].新技术新工艺.2009,(6):52-53.
The finite element analysis on the contact stress for angular contact roll bearing
TH12
A
1009-0134(2016)06-0111-03
2016-03-13
国家自然科学基金面上项目(41272174);武昌首义学院校内科研资助项目(XK1501)
高恒强(1977 -),男,河北石家庄人,讲师,硕士,主要从事机械设计与自动化方向的研究。

