基于弹性流体动力学的曲轴系统仿真分析
张琼宇,王奎,朱小平(中船动力研究院有限公司,上海200129)
基于弹性流体动力学的曲轴系统仿真分析
张琼宇,王奎,朱小平
(中船动力研究院有限公司,上海200129)
以某船用柴油机为研究对象,进行曲轴主轴承载荷计算及对比分析。采用多柔体动力学计算主轴承载荷,柔体之间应用弹性流体动力学耦合。结果显示,液动轴承耦合的动力学结果更接近真实情况,曲轴主轴承各部分载荷分布并不均匀,容易造成偏磨,同时,为曲轴主轴承设计及曲轴受力分析提供了重要依据。
主轴承 柔性多体系统动力学 弹性流体动力学
1 引言
在发动机实际工作过程中,曲轴系统受到活塞连杆传递的交变载荷,受力情况比较复杂。传统上对曲轴系统动力学的研究,多采用刚柔耦合的多体动力学分析。对于刚体与柔体、或柔体与柔体的耦合,多采用单节点直接耦合的方式。实际上,由于忽略了轴承润滑,单节点耦合方式在传递载荷时,无法考虑轴承区域的载荷分布不均匀[1]。本文运用模态分析、柔体多体动力学、弹性流体动力学技术,对某新型船用中速柴油机进行动态仿真,分析液动轴承对曲轴主轴承受力的影响。
2 数学模型
2.1柔性体基本理论
柔性体采用修正的Craig-Bamptom模态法,用少数低阶模态描述复杂的动力学特性[1]。柔性体位移方程为

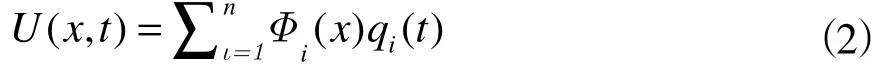
Φi(x)组成模态矩阵,qi(t)为振型系数。将式(2)代入式(1)得模态坐标下的位移方程为
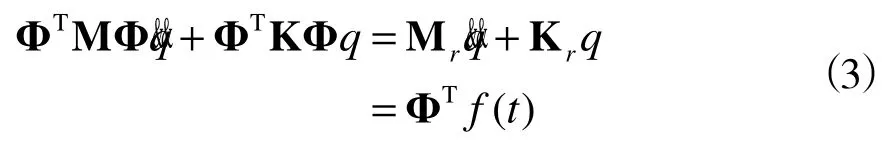
2.2柔性体动力学方程
曲轴轴颈受到油膜压力及外载荷共同作用,其动力学方程为[2]

轴承轴瓦动力学方程为

2.3连接柔性体弹性动力润滑轴承的雷诺方程
曲轴主轴颈与轴瓦直接采用弹性液动润滑轴承连接。流体动力润滑的扩展雷诺方程为
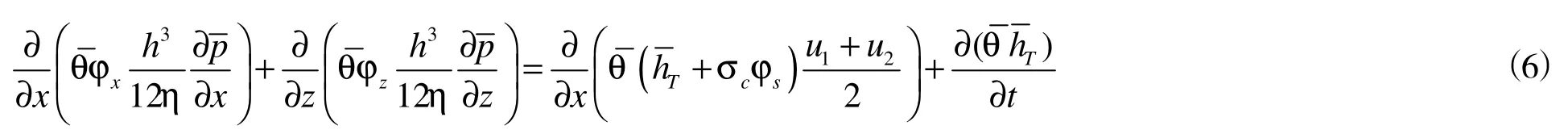
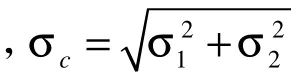
3 建立刚体模型
Virtual Engine中的模型基于参数化建模思想,只需要输入柴油机基本参数,如缸径、缸数、发火顺序、缸心距等,就可以创建最基本的曲轴模型,如图1所示。再通过修改各部件(曲轴、连杆等)的尺寸、质心坐标、转动惯量等基本信息,导入气缸压力曲线、润滑油参数等就可以创建曲轴刚体模型[5]。用四面体单元进行网格划分[6]。
在生成柔性体中,最重要的就是定义连接点。主轴承及曲柄销轴承都采用的是弹性液动轴承,在曲轴主轴颈及曲柄销上沿着轴线方向均匀分布3个RBE3点如图2(a)所示,每个RBE3分别绑定对应轴颈处外表面节点,如图2(b)所示,RBE3点位移的受被绑定节点位移控制。考虑到计算效率,应该约束RBE3的部分自由度[7],减小计算规模,曲柄销(P1)主要受径向力与切向力,所以仅保留径向及切向自由度。曲轴止推轴承处主轴颈(M2)不但受到径向力和切向力,还受到来自止推轴承对其的轴向力,其他主轴颈(M1)仅受径向力和切向力。曲轴在飞轮处(S3)受到飞轮对其的扭矩,所以保留其轴向的转动自由度,如图3所示。
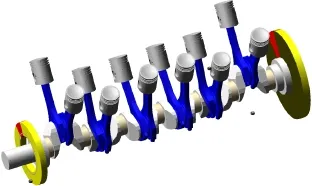
图1 曲轴系统刚体模型
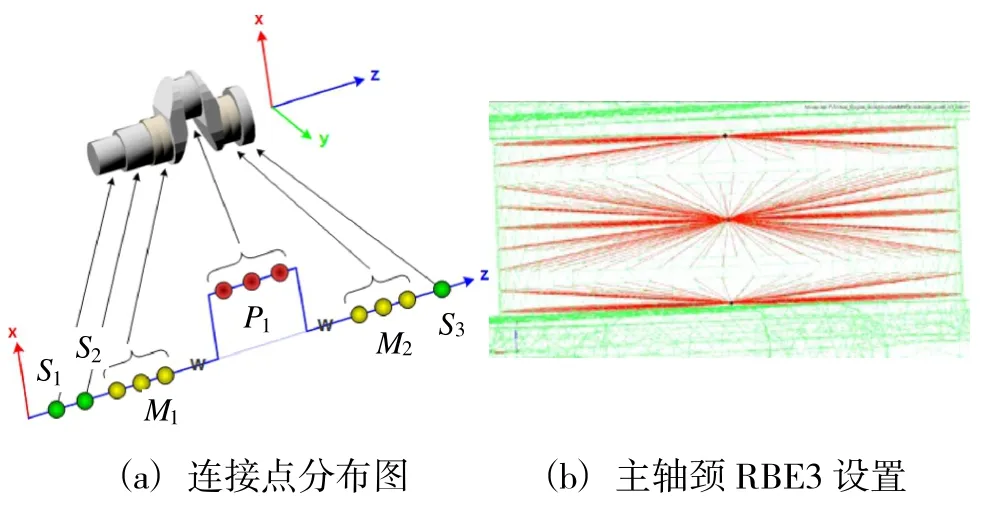
图2 连接点设置
4 建立曲轴系统柔性体模型
VirtualEngine中柔性体基于模态理论,主要步骤如下:(1)对曲轴、连杆、机体进行网格划分,同时定义连接点;(2)用有限元软件进行模态分析得到模态中性文件(MNF);(3)将曲轴、连杆、活塞的模态中性文件导入多体系统中,设置轴承类型,求解计算。
4.1生成曲轴、连杆、机体的柔性体文件
将曲轴、连杆、机体的三维几何模型导入Hypermesh进行网格划分,对曲轴、连杆、机体采
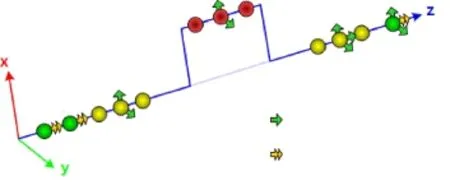
图3 RBE3自由度
将划分好网格及定义完连接的曲轴、连杆、机体提交给Nastran进行模态分析,得到模态分析结果及模态中性文件(MNF文件)。由于系统低阶模态的固有频率对系统的动力学响应影响最大,因此对于曲轴、连杆、机体一般只计算前20阶主要模态[8]。
4.2建立曲轴系统柔体模型
将生成的曲轴、连杆、机体的柔性体文件(MNF)导入Virtual Engine中,替换刚体的曲轴、连杆、机体,如图4所示。
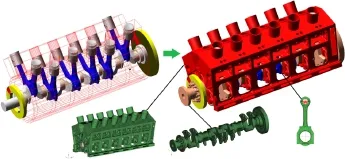
图4 曲轴柔体模型
5 仿真结果及分析
5.1模型验证
为验证所建动力学模型及仿真结果的正确性,将刚体模型的结果与理论计算结果比较,图5为第3档主轴承载荷。可以看出刚体模型结果与理论计算基本一致,存在的细微不同,主要是理论计算使用的数学模型相对简化,未考虑部分惯性力、重力等。图5的结果充分证明了所建动力学模型的正确性,为下文的研究奠定了基础。
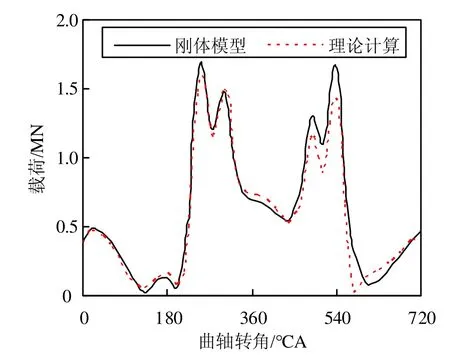
图5 刚体模型和理论计算第3档主轴承载荷
5.2曲轴曲柄销受力
柔体动力学的曲柄销受力情况如图6所示,由于柔体曲轴在受到外力作用下会产生变形,且变形并不一致。因此各个曲柄销的受力并不完全相同,存在细微变化,尤其是在最大爆发压力处,曲轴变形最大,影响了曲柄销的实际受力情况。
比较刚体模型与柔体模型的第2档曲柄销受力情况,如图7所示。柔体变形降低了最大载荷,但使最小载荷增加了,由于减小了载荷峰值,所以曲柄销的受力情况有所改善。
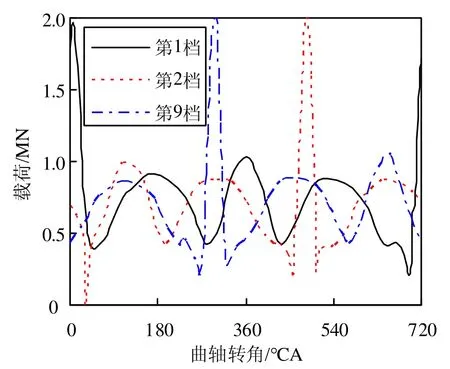
图6 曲柄销受力
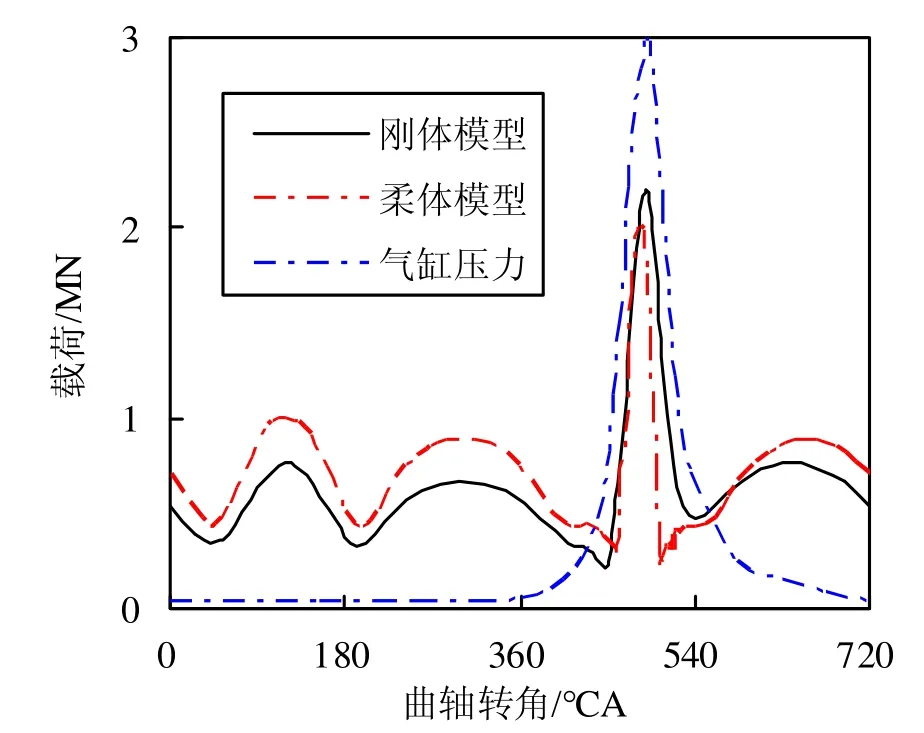
图7 刚体模型与柔体模型第2档曲柄销受力对比
5.3曲轴主轴承载荷对比
柔体动力学的曲轴主轴颈与机架上的主轴承通过高度非线性的弹性流体液动轴承耦合,得到各个主轴承的载荷,而普通多体动力学则通过节点直接耦合。通过比较可以看出,液动轴承耦合的柔性体轴承受力与普通刚体轴承的受力并不完全一致,尤其在最大受力处,柔性体曲轴受力后变形,使柔性体的曲轴轴承受力略大于刚体轴承受力,如图8所示。第1档和第7档主轴承主要受单侧两缸爆发压力影响,最大载荷都出现在单侧两缸最大爆压之间,分别为1.79MN和1.77MN;第2档至第6档主轴承都出现2个波峰,为相邻两侧四缸爆发压力所致,每个波峰都出现在单侧两缸最大爆发压力之间,其中第2档轴承在68°时,峰值载荷达到了2.47MN,易引起轴承与轴颈间的干摩擦。
5.4曲轴主轴承各部分受力

图8 各档主轴承受力对比

图9 轴瓦划分为3个部分
在主轴承受力分析中,将轴瓦分为三部分,即左边、中心、右边,其分割如图9所示。图10为档至第6档主轴承同时承受两侧气缸爆发压力,在一个周期内(720℃A),轴承的左右两边分别承受一个峰值载荷,轴承的磨损较为均匀。
5.5轴承载荷分布
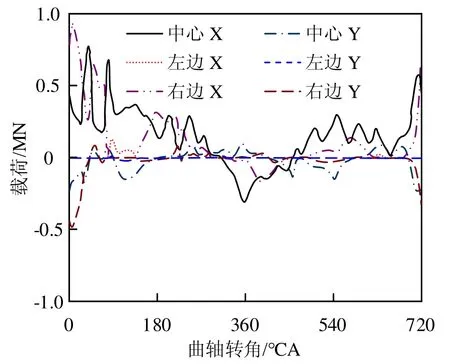
(a)第1档主轴承轴瓦三部分载荷
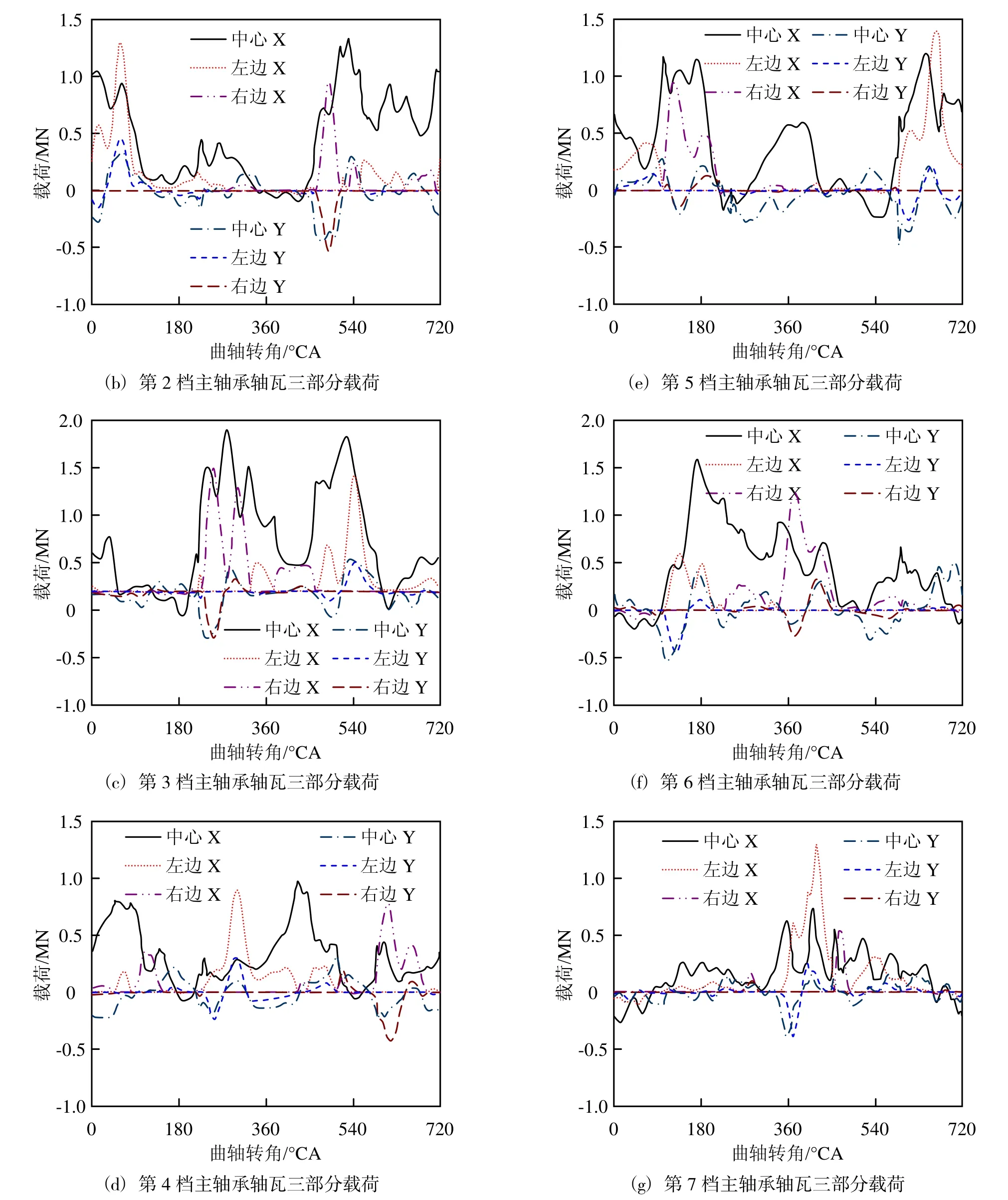
图10 各主轴承轴瓦三部分载荷
在传统近似计算中,轴承载荷都是以余弦分布各档轴承轴瓦的三部分载荷。显然第1档主轴承轴瓦右边的受力明显大于左边,X方向最大值为0.937MN,出现在第1缸最大爆发压力附近。这是由于第1档主轴承只承受右侧两缸的爆发压力,所以右边受力比较大,磨损也比较严重;第7档主轴承由于只受左侧两缸爆发压力影响,也存在偏磨现象,在419℃A时X方向最大值为1.30MN;第2的形式加载在轴承上。但在曲轴轴承中,其载荷分布并不是余弦分布,图11为第1档~第7档主轴承的第1个最大峰值载荷沿轴向的分布。大部分载荷的分布都是一定斜率的斜线,这是由于峰值载荷主要由主轴承单侧两缸的爆发压力影响,爆发压力侧的轴承载荷显著大于另一侧,导致载荷分布呈斜线分布。而在近似计算中,认为载荷在轴承中心,所以轴承载荷按照余弦分布。第6档主轴承峰值载荷基本按照余弦分布,这是由于第6档主轴承两侧气缸发火时间相近,两侧爆发压力在第6档主轴承两侧形成平衡,可等效为轴承中间的集中力,所以主轴承载荷分布呈余弦分布,如图12所示。

图11 主轴承轴承载荷分布

图12 曲轴主轴承载荷分布
6 总结
在柴油机多体动力学分析中,柔性体部件之间通过弹性流体动力轴承的耦合,能够更加准确地模拟柴油机运行过程中轴承的真实的受力情况,其计算结果更加接近实际。曲轴主轴承载荷并不是余弦分布的,大部分载荷都是斜线分布。
[1]赵小勇,孙军,刘利平等.不同工况下内燃机曲轴轴承的润滑性能[J].内燃机学报,2011,29(4):348-354.
[2]魏立队,段树林,武起立等.船用柴油机曲柄连杆机构与机体非线性耦合的数值仿真[J].大连海事大学学报,2012,38(1):89-93.
[3]武起立,段树林,邢辉等.二冲程船舶柴油机主轴承润滑数值分析[J].大连海事大学学报,2011,37(4):25-29.
[4]程人杰,樊文欣,王东娇.基于柔性多体动力学的发动机主轴承润滑仿真分析[J].小型内燃机与摩托车,2010,39(2):19-22.
[5]胡爱闽.基于ADAMS的柴油机曲轴系统多体动力学仿真[J].煤矿机械,2010,31(2):62-65.
[6]肖民,史万强.6L21/31型船用中速机柴油机动力学仿真及曲轴应力分析[J].船海工程,42(1):114-117.
[7]李玉军,杨建国.4120SG型柴油机曲轴系统动力学仿真与分析[J].武汉理工大学学报,2007,31(1):73-76.
[8]张坤金,郑忠才,高岩等.不同网格划分对机体有限元模态分析结果的影响[J].小型内燃机与摩托车,2009,38(5):69-71.
Dynamics Simulation Analysis of Crankshaft System Based on Elasto Hydrodynamic Lubrication
Zhang Qiongyu,Wang Kui,Zhu Xiaoping
(China Shipbuilding Power Engineering Institute Co.,Ltd,Shanghai200129,China)
Load of crankshaftmain bearing in amarine diesel engine was analyzed.Load ofmain bearing was calculated by Flexible Multi-Body dynamics combining elasto hydrodynamic lubrication. Results show that coupled dynamics of hydrodynamic bearing ismore real.The load distribution ofmain bearing is nonuniform and will cause eccentrically-wearing.In addition,the results can be referenced for design ofcrankshaftandmain bearing.
main bearing,flexiblemulti-body dynam ics,elasto hydrodynam ic lubrication
10.3969/j.issn.1671-0614.2016.02.002
来稿日期:2015-10-09
张琼宇(1988-),男,助理工程师,主要研究方向为发动机结构设计。

