基于CFD的双调距桨桨叶应力及变形仿真分析

颜昌禄,刘正林

(1.中国船级社 广州分社，广州 510235; 2.武汉理工大学 能源与动力工程学院，武汉 430063)



基于CFD的双调距桨桨叶应力及变形仿真分析

颜昌禄1,刘正林2

(1.中国船级社 广州分社，广州 510235; 2.武汉理工大学 能源与动力工程学院，武汉 430063)

以双调距桨为研究对象，应用CFD方法(FLUENT和ANSYS Workbench 软件)，分别建立有限体积元模型和有限元模型，将有限体积元模型仿真计算得到的桨叶三维水动力载荷施加在有限元模型的桨叶叶面上，进行双调距桨桨叶的应力及变形的仿真计算与分析，揭示双调距桨的桨叶应力与变形随螺距角、进速系数的变化规律，为调距桨的设计与优化提供理论支持。

双调距桨；桨叶应力；桨叶变形；有限体积元模型；有限元模型

随着船舶大型化、现代化和自动化的发展，调距桨尺寸也越来越大，对性能的要求也越来越高，但目前国内外在船舶调距桨的桨叶应力与变形，尤其是双調矩桨(包括双桨的干扰问题)的仿真计算鲜有报道。

调距桨[1-8]在工作时，工况多变、受力复杂，作用在桨叶上的轴向推力和旋转阻力使得桨叶产生弯曲和扭转，局部出现较大的应力与变形。为了保证调距桨桨叶拥有足够的强度，在工作中不发生损坏及断裂事故，须对调距桨桨叶的应力与变形及影响因素(如螺距角、进速系数等)进行分析计算，为调距桨的设计与优化提供理论支持。

1　双调距桨桨叶强度计算模型

双调距桨在正常工作时受到的载荷主要包括水动力载荷、重力载荷，以及离心力载荷。其中，重力载荷和离心力载荷比较容易确定，关键问题是解决桨叶在调距过程中所受到的水动力载荷的大小和分布及双桨干扰问题。双调距桨的水动力载荷可应用计算流体动力学(computation fluid dynamics，CFD)方法(FLUENT和ANSYS Workbench 软件)，分别建立双调距桨的有限元体积模型和有限元模型，将有限元体积模型计算得到的桨叶三维水动力载荷施加在调距桨有限元模型的桨叶叶面上，进行双调距桨桨叶的有限元分析，得到调距桨桨叶应力及变形场分布状况。由于2个调距桨为对称分布，其桨面压力、速度等分布状况相同，因此仅以单桨为例进行仿真计算与分析。

1.1调距桨类型及主要参数

某船的推进器为AU型双调距桨，旋向为外旋。其他相关几何参数见表1。

表1　螺旋桨的参数

1.2 计算域网格划分及边界条件设置

1)调距桨网格划分。应用GAMBIT将调距桨桨叶各个截面上的三维型值点拟合成光滑的曲线，由线生成面，面合成体，生成三维桨叶模型，见图1a)。通过软件整合功能将所有零部件并成一体，组成完整的调距桨。调距桨表面网格选用三角形类型，采用手动方式对桨叶的网格尺度进行定义，并对桨叶叶梢、导边、随边和桨毂等结合部位的网格加密，见图1b)。

图1　调距桨模型及网格划分

2)计算域网格划分。以船体中线为轴线，将建好的调距桨三维模型进行镜像阵列，得到2个旋向相反的调距桨。2个螺旋桨在同一截面上，2桨轴线间距为2.5D(D为调距桨直径)。

工作时，调距桨周围流体随桨一起转动。为了模拟调距桨周围的流场，在调距桨外部创建一个大型圆柱体作为流场控制体。控制体长10D，直径6D。流场区域分成两部分：将调距桨四周设为圆柱体旋转区域，旋转区域长0.8D，直径1.6D，用来仿真模拟调距桨周围流体的流动；除旋转区域外，流场区域的其余区域设为静止区域。

对圆柱形流场区域划分网格时，采用非结构化网格(Tet和Hybrid混合单元)，见图2。模型整个流场节点数有20多万个，网格单元有300多万个，其中，最大体网格体积为0.12 mm3，而最小体网格体积只有0.041 5 mm3。

图2　计算域网格划分侧视

3)边界条件。在调距桨水动力的敞水计算中，选用FLUENT软件中的多重旋转坐标系模型(即MRF模型)。进口为速度进口，出口为自由出口；流体湍流模型采用k-ε计算模型。外部静止区域的圆柱体表面设置为壁面(WALL)，内部旋转区域与外部圆柱静止区域间重合的圆柱体表面设为INTERFACE面。在导入FLUENT后将这2个重合表面连接起来，形成一对交接面，以便于外部静止区域与内部旋转区域的数据和能量的交换。调距桨表面边界条件设定为壁面(WALL)，在导入FLUENT后成为与内部旋转区域同轴旋转的旋转壁面。整个流域的边界条件见图3。当调距桨转速为360 r/min，进速系数J=0.5，速度进口为10 m/s时，调距桨的桨叶叶面压力分布云图见图4。

图3　整体模型计算域边界条件示意

图4　螺距角35°时叶面压力云图

1.3双调距桨有限元模型和桨叶载荷

调距桨结构静力学分析需要调距桨实体有限元模型，而调距桨流场模拟需要调距桨外部流场模型(有限体积元模型)。但这2种模型的网格节点在调距桨桨叶交界面处不一定能一一对应，须遵循空间距离就近原则，应用ANSYS Workbench软件将该处的2种网格节点一一配对，然后将在调距过程中由有限体积元模型计算得到的桨叶表面的水动力载荷信息完全映射到调距桨有限元模型的桨叶表面，然后进行桨叶应力和变形仿真计算。加载后的调距桨叶面和叶背有限元模型见图5。

图5　加载后调距桨荷限元模型

2　桨叶应力及变形有限元分析

计算中假定进速系数J=0.3、0.5、0.7，转速n=360 r/min，桨叶螺距角为35°、10°、0°和-20°，应用ANSYS Workbench软件，对调距桨在调距过程中的应力与变形状况进行分析。

1)调距过程中桨叶的应力场分析。当J=0.5，其他条件不变时，叶面的等效压力分布见图6。

图6　不同螺距角时桨叶的等效压力颁云图

由图6可见，虽然调距桨螺距角不同，但应力集中区域均出现在桨叶叶根处，应力由桨叶叶根到叶梢逐渐减小；螺距角为35°时，最大应力为61.479 MPa。桨叶叶面和叶背应力分布规律基本相同，都在桨叶叶根处出现应力集中区域，最大应力为61.497 MPa，与叶面几乎相等，见图6a)和图7所示。因此，桨叶叶根处的强度问题在设计中须重点考虑。

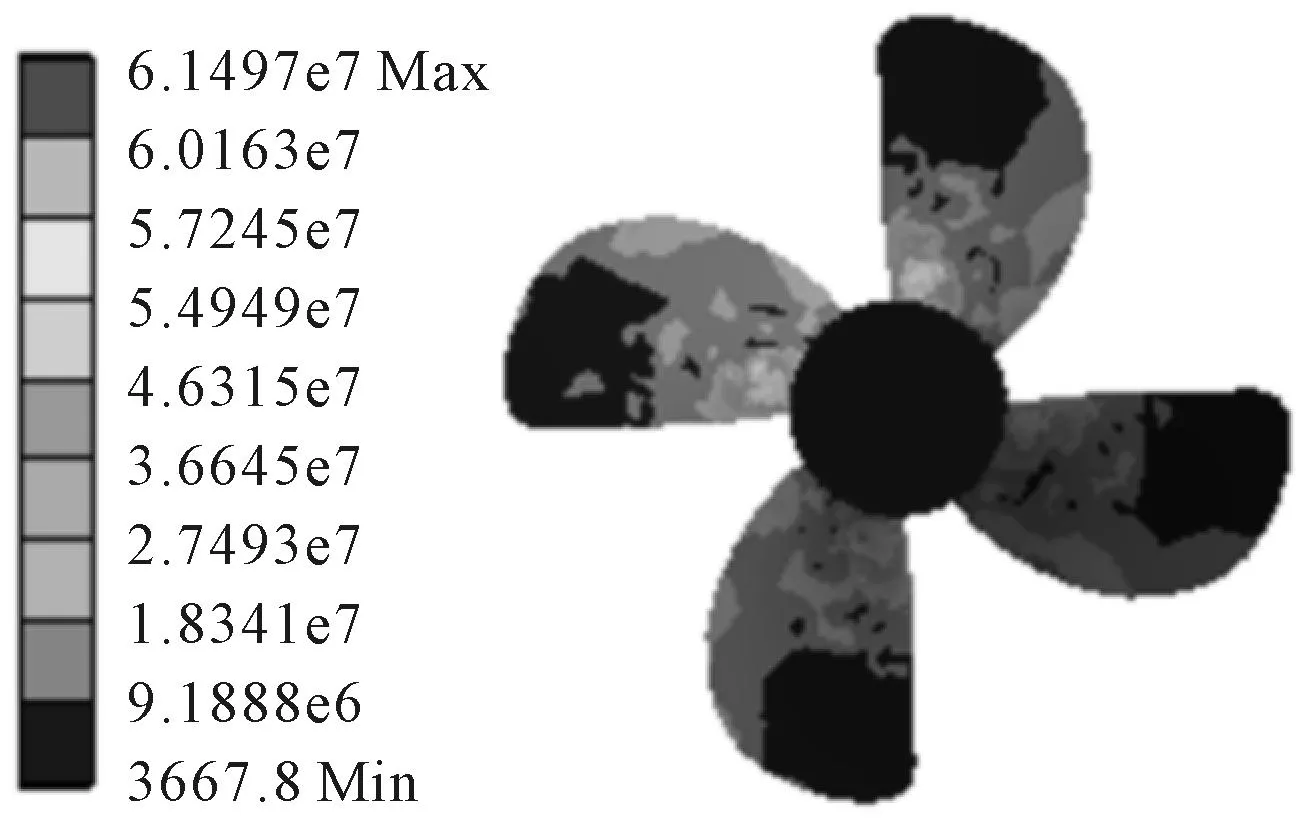
图7　螺距角为35°时叶背等效压力分布云图

当进速系数J=0.3、0.5、0.7时，桨叶在不同螺距角下的最大应力变化状况见图8。

图8　调距中桨叶最大应力变化

由图8可知，当调距桨由最大正车螺距角35°变为最大倒车螺距角-20°的过程中，桨叶最大应力值先逐渐减小，在螺距角为0° 左右时达到最小，然后再逐渐增大。与最大正车螺距角的应力场分布相比，最大倒车螺距角更加复杂，最大应力值也比较大。在桨叶螺距角相同时，随着进速系数的增加，桨叶最大应力值会逐渐降低。

2)调距过程中桨叶的扭曲与变形。在调距过程中，调距桨桨叶在水动力等因素的共同作用会产生一定程度的扭转和弯曲变形。当J=0.5，其他条件不变时，桨叶叶面变形见图9。

图9　不同螺距角时桨叶的叶面变形分布云图

由图9可见，虽然调距桨螺距角不同，但最大变形均出现在桨叶叶梢处，由叶梢到叶根逐渐减小。当螺距角为-20°时，叶面最大变形量为0.000 797 m。桨叶的叶背变形云图与叶面变形云图基本一致，见图9a)和图10所示。

图10　螺距角为35°时叶背变形分布云图

当调距桨进速系数J=0.3、0.5、0.7时，不同螺距角的桨叶叶面最大变形量见图11。

图11　调距中桨叶最大变形量变化

由图11可见，当调距桨由最大正车螺距角35°变为最大倒车螺距角-20°的过程中，桨叶最大变形的变化规律与图8相同。最大倒车螺距角的桨叶变形量大于最大正车螺距角。当桨叶螺距角相同时，随着进速系数的增加，桨叶最大变形量逐渐减小。

3　结论

1)在双调距桨桨叶叶根处出现应力集中区域，应力从桨叶叶根到叶梢逐渐减小；叶梢处变形最大，从叶梢到叶根逐渐减小。桨叶叶面和叶背的应力与变形分布规律基本相同。

2)当调距桨螺距角由35°变为-20°的过程中，桨叶最大应力值先逐渐减小，在螺距角为0° 左右时达到最小，然后再逐渐增大。倒车时的应力场分布比较复杂，不同螺距角的最大应力值均高于相应的正车螺距角。当桨叶螺距角相同时，随着进速系数增加，桨叶最大应力值逐渐降低。

3)当调距桨螺距角由35°变为-20°的过程中，桨叶最大变形的变化规律与最大应力相同。当桨叶螺距角相同时，桨叶最大变形随着进速系数的增加而减小。

今后应继续探讨双调距桨布置方式(桨与桨间距、桨轴线的纵倾角与外张角)对调距桨的桨叶应力与变形的影响，为提高调距桨的可靠性及推进效率提供技术支持。

[1] 黄毅，许辉，姜治芳．大侧斜螺旋桨强度校核探讨[J].中国舰船研究，2010(10)：44-48.

[2] 刘竹青，陈奕宏，姚志崇．基于面元法及有限元法耦合的螺旋桨强度计算[J].中国造船，2012(6)：25-29.

[3] 田斌斌，姜治芳，朱英富．侧斜螺旋桨桨叶强度计算及其可靠性分析[J].舰船科学技术，2002，24(6)：10-12.

[4] 杨琼方，王永生，刘承江.调距桨调距过程中叶元体受力的CFD分析方法研究[J]．船舶力学，2010，14(5)：458-465.

[5] ANDREW Kendrick，P Eng L Blair Carroll. Laurent propeller damage analyses[R]．Canada：Transportation Development Centre Transport Canada，2003.

[6] SZANTYR J A. The crucial contemporary problems of the computational methods for ship propulsor hydrodynamics[J]．Archives of Civil an Mechanical Engineering，2008，8(1)：69-95.

[7] Stern,Wilson，COLEMAN R F. Comprehensive approach to verification and validation of CFD simulations,Part 1：Methodology and procedures[J]．ASME J.Fluids Eng，2001(3)：793-802.

[8] Stern，Wilson，COLEMAN R F. Comprehensive approach to verification and validation of CFD simulations，Part 2：Application for RANS simulation of a cargo/container ship[J]．ASME J.Fluids Eng，2001(4)：803-810.

Simulation Analysis on Stress and Deformation of Twin Controllable Pitch Propeller Blades Based on CFD

YAN Chang-lu1, LIU Zheng-lin2

(1.Guangzhou Branch of China Classification of Society, Guangzhou 510235, China;2.School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China)

Both finite volume element model and the finite element model of twin controllable pitch propeller are established with CFD method including FLUENT and ANSYS Workbench software respectively. The three-dimensional hydrodynamic loads of the propeller blade which are obtained by finite volume element model are applied upon the propeller blade surface of the finite element model, to carry out the simulation of stress and deformation of the propeller blades. The numerical results reveals the variation law of stress and deformation of the controllable pitch propeller blades with pitch angle and advance coefficient, and provides the theoretical support to design and optimization of the controllable pitch propeller.

twin controllable pitch propeller; blade stress; blade deformation; finite volume element model; the finite element model

2016-07-07

2016-07-10

国家自然科学基金(51379168, 51139005)

颜昌禄(1984—)，男，硕士，工程师

U664.31

A

1671-7953(2016)04-0141-04

DOI:10.3963/j.issn.1671-7953.2016.04.033

研究方向:船舶动力装置

E-mail:clyan@ccs.org.cn