不同畸变模型在航摄相机校准中的适用性研究

黄留波

（广西水利电力勘测设计研究院，南宁 530023）

不同畸变模型在航摄相机校准中的适用性研究

黄留波

（广西水利电力勘测设计研究院，南宁 530023）

分析了航摄相机光学畸变原理及主要误差源，分别利用10参数模型、一般多项式模型和有限元模型在航摄相机校准中的适用性进行了实验比较，结果表明10参数模型和多项式模型校准精度优于1 μm，优于有限元模型。

10参数模型；多项式模型；有限元模型；光学畸变

0 引言

航摄相机光学系统在设计、制作和装配过程中，存在像差、角放大率的变化、有效光阑位置的变化、光瞳中心与主点不重合以及各透镜的偏心等问题，破坏了系统的消畸变性和对称性，形成了摄影物镜的畸变。相机畸变导致物点、镜头中心以及像点不再满足共线条件，测量必然出现误差[1]。为了更好地进行摄影测量型相机校准，目前针对相机畸变模型[2]的研究越来越多。冯其强等人[3]针对数字工业测量相机检校问题，提出在10参数相机畸变模型基础上加入有限元模型二次检校，通过对INCA3测量相机和Cannon EOS 5D Mark 2非测量型相机比较试验发现测量型相机精度改善很大，非测量型相机效果不明显；丁昊等人[4]提出了一种无需控制场，仅采用影像线特征进行非量测相机畸变测定方法，并进行了可行性分析论证；程效军等人[5]通过分析数字相机的结构和误差来源，提出一种针对数字相机畸变差检测的严密数学模型，并运用序贯方法解算该模型；冯文灏等人[6]提出并论证了基于二维直线线性变换的畸变校正方法，发现该方法特别适用于各类固态相机（CCD，CID，PSD）的畸变模型建立。本文对目前主要的3种畸变模型即10参数模型、多项式模型和有限元模型进行了系统研究和实验比较，并对航摄相机进行了实际检校测试，为航摄相机畸变数学模型的选择提供了理论支持。

1 基本原理

1.1 光学畸变原理

畸变差根据产生的原因可以分为两种：对称畸变和非对称畸变。其中对称畸变由于物镜残余像差引起，并使得像点径向产生偏差，主要分为枕形畸变和桶形畸变[6]，其中枕形畸变相对主点向外产生偏移，桶形向内（如图1所示）。

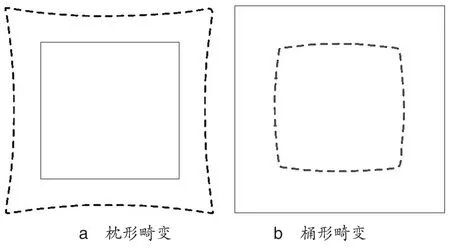
图1 两种径向畸变示意图

径向畸变：

将其分解到像平面坐标系的x轴和y轴上，则有：

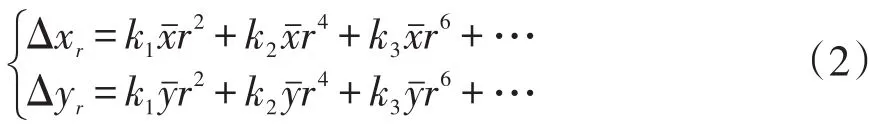
偏心畸变：

分解到像平面坐标系的x轴和y轴上，则有：

其中：p1,p2为偏心畸变系数，偏心畸变在数量上比径向畸变小的多。

像平面内的平面畸变和像平面不平引起的畸变都包含了透镜误差，其表达式为：

式（5）中b1，b2为像平面内畸变系数。假设设传感器焦距变化量为Δf，传感器镜头主点坐标偏移量为Δxp,Δyp表示，该变化量在像点上的影响为：

1.2 相机畸变模型

1.2.1 10参数模型

10参数模型涵盖了目前已知的几乎所有物理影响因素。该模型真实反映了在成像过程中所产生的系统误差，而且在算法上更加容易实现，精度更高，是相机畸变校正最为成熟的模型。10参数模型的每一个畸变参数都有明确物理含义，如镜头器件光学中心不共线引起的偏心畸变等。摄影物镜的畸变差包括对称径向畸变、偏心畸变和像平面畸变。10参数数学模型公式表达如下[8]：

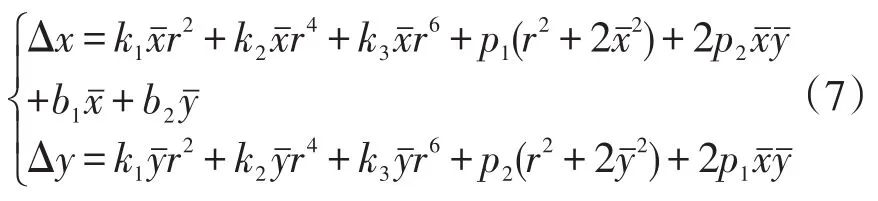
径向畸变系数：k1，k2，k3；

偏心畸变系数：p1，p2；

像平面畸变系数：b1，b2。

根据附加参数光束法平差得到的系统畸变系数，通过间接纠正来逐个点去校正系统畸变差。

1.2.2 多项式模型

一般多项式模型采用关于像点坐标（x，y）的二元n次多项式。一般多项式模型如下式所示[8]：

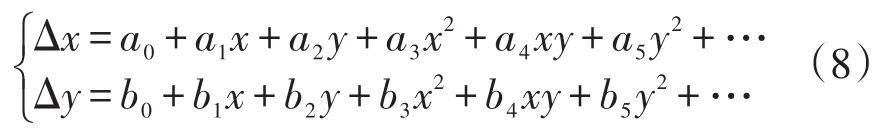
像点坐标畸变：（Δx,Δy）；

像点坐标：（x，y）；

像点畸变系数：a0，a1，b0，b1等。

一般多项式模型是整体模型，其中的参数并没有明确的物理意义，而是将像点畸变看作整体去校正，该模型由于物理意义不明显，因此较多的研究只涉及理论，现实畸变校正应用较少[7]。

1.2.3 有限元模型

有限元方法目前已经广泛应用在数字地面模型、相机检校等领域，该模型可以拟合一般情况下很难利用参数模型拟合的焦平面产生的系统差[9]，该模型主要分为补偿主距变化和直接补偿像点畸变两类。其中，补偿主距变化是把光学畸变看作各个像点主距值变化，从而进行补偿，主要针对径向和像平面不平引起的畸变。第二类是直接补偿各像点畸变，即将像平面等分为若干单元，像平面内任意一点畸变都能利用该单元4个节点双线性内插，同时需要加入一些连续性约束条件保证畸变连续性。

2 畸变校正实验

航摄相机畸变校正的基本要求是建立的数学模型尽量逼近实际测量结果，逼近的程度可用一种偏差的平方和表示。假定通过相机校准测量得到的畸变为Δ'xi和Δ'yi，通过畸变模型拟合公式得到的畸变为Δxi和 Δyi，令，则畸变校正精度为。数字航摄相机的畸变校正过程中，求取各畸变模型公式的参数，就是一个优化计算的过程，优化的目标就是使σ最小，也就是要求数学模型与实际测量结果最接近。在数字航摄图像的后处理时，用这些几何标定得到的参数，重新计算和修正每个像素的坐标，以便获得地面图像的高精度几何位置数据。

为对各模型的校正精度进行评价，利用航摄相机畸变测量仪标准装置，对标称焦距为88mm、152mm、300mm的航摄相机进行分别校准，解算其内方位元素和畸变系数，利用10参数模型、多项式模型和有限元模型进行畸变校正，实验结果如下。

2.1 10参数模型畸变校正实验

10参数模型畸变校正精度结果见表1。

实验表明：含k1、k2和含k1、k2、k3的10参数模型的校正精度相差较大，因此，在利用10参数模型进行航摄相机畸变校正时，径向畸变系数取k1、k2、k3。

2.2 多项式模型畸变校正实验

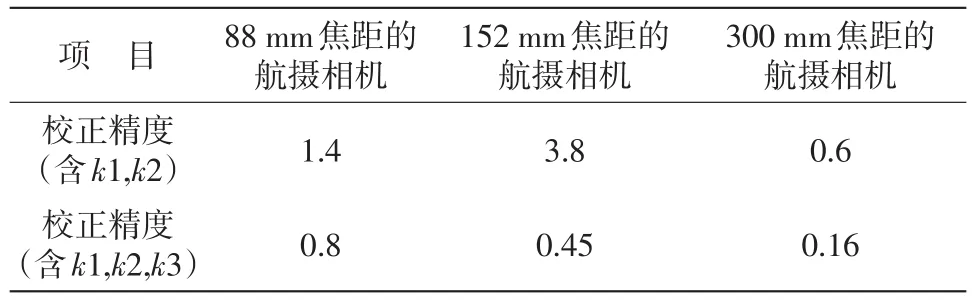
表1 10参数模型校正精度 μm

利用多项式模型畸变校正精度结果如表2所示：

表2 多项式模型畸变校正精度 μm

2.3 有限元模型畸变校正实验

采用补偿主距变化的有限元方法进行相机畸变校正，即将畸变视为由各采样点处的主距值变化引起，那么 Di=Δftanαi，αi为第i个采样点对应网络中心的角度，Di为第i个采样点的径向畸变差。利用有限元模型进行畸变校正，结果如表3所示：

表3 有限元模型畸变校正精度 μm

2.4 实验比较与分析

通过以上实验分析可以得出以下3个结论：

（1）10参数模型的纠正精度随着主距的增大而提高，多项式模型的校正精度随着主距的增大而降低，有限元模型的校正精度随着主距的增大变化不明显；

（2）对不同焦距的航摄相机，含k1、k2、k3的10参数模型的畸变校正精度均优于含k1、k2的10参数模型，因此，在利用10参数进行畸变校正时，径向畸变系数应取k1、k2、k3；

（3）对不同焦距的航摄相机，而多项式模型和10参数模型的畸变校正精度均优于1μm，均优于有限元模型。

3 结论

航摄相机畸变差校准是一个十分重要且复杂的问题。畸变模型各有优势，对于不同测量型或者非测量型相机都有不同的适用性[10]。10参数模型中各畸变参数具有明确的物理意义，因此对于可以预见的畸变差都可以很好的校正，在对3种主距的航摄相机校正中表现稳定，精度较高，应用也最为普遍。从实验结果来看，有限元模型校正精度稳定在1μm，但比多项式模型和10参数模型要差一个数量级，因此通过实验比较，建议航摄相机畸变模型采用10参数模型或多项式模型，校正精度更高。

[1] 黄 静.照相物镜径向畸变模型的再商讨[J].光学学报，2008（10）：1930-1933.

[2] 金仲华，崔红霞.数字相机径向畸变差检测及改正[J].科技广场，2008（10）：118-120.

[3] 冯其强.数字工业摄影测量技术研究与实践[D].郑州：信息工程大学博士论文，2010.

[4] 丁 昊，谢文寒，张继贤.无控制场的相机畸变差改正方法[J].测绘科学，2012，37（2）：33-35.

[5] 程效军，胡敏捷.数字相机畸变差的检测[J].测绘学报，2002（S1）：113-117.

[6] 冯文灏，商浩亮，侯文广.影像的数字畸变模型[J].武汉大学学报（信息科学版），2006，31（2）：99-103.

[7] 冯文灏.关于近景摄影机检校的几个问题[J].测绘通报，2000（10）：1-3.

[8] 黄 静.大面阵数字航测相机的精密几何标定[J].光电工程，2006，133（2）：138-140.

[9] 李德仁，袁修孝.误差处理与可靠性理论[M].武汉：武汉大学出版社，2002.

[10] 詹总谦，张祖勋，张剑清.基于LCD平面格网和有限元内插模型的相机标定[J].武汉大学学报（信息科学版）2007，32（5）：394-397.

（责任编辑：刘征湛）

Study of adaptability of different distortion model in aerial photographic camera calibration

HUANG Liu-bo
（Guangxi Water and Power Design Institute,Nanning 530023,China）

A brief analysis was made on the optical distortion Princciple and main error sources of aerial photographic camera.Tests were conducted to study the adaptability of 10-parameter model,polynomial model and finite element model in aerial photographic camera calibration.The results of test demonstrate that 10-parameter model and polynomial model are better than finite element model with calibration accuracy superior to 1μm.

10-parameter model;polynomial model;finite element model;optical distortion

P236

B

1003-1510（2016）04-0024-04

2016-04-12

黄留波（1986-）男（壮族），广西马山人，广西水利电力勘测设计研究院工程师，学士，主要从事水利水电工程测量工作。