浅议内外管压差流量计压损的影响因素

陈 瑛 程焕焕

绍兴市能源检测院



浅议内外管压差流量计压损的影响因素

陈 瑛 程焕焕

绍兴市能源检测院

内外管差压流量计是目前极为重要的一种流量计，而其在具体的操作中也会造成压损，本文主要对内外管压差流量计压损的影响关键因素进行了全面科学探讨，以此可以给相关的从业人员一点建议。

内外管；流量计；影响因素

前言

内外管差压流量计是一种新型差压式流量计。该流量计设计的取压位置为管的同一截面上，消除了节流件前后摩阻压降对压差信号的影响，相同的流量下，获得的压差信号较传统的压差流量计大，提高了信号的灵敏度，其节流方式较传统流量计对流体的扰动减小，提高了压差信号的稳定性；在相同的压差信号下，其压力损失比内锥式流量计要小很多，符合作为相关能源测量的要求。但是，目前对影响内外管压差流量计压力损失的具体因素研究较少，而研究关键因素对该流量压损的影响有助于该流量计优化设计，为其设计提供一定的指导意义。

1 基本结构及理论

（1）基本结构

内外管压差流量计结构如图1所示，流量计以管道轴线定位安装，主体结构由前直管段（大径d1）、梯形段、后直管段（小径d2）组成，外取压口在管道壁上取流道2的压力，内取压口在支架中空取流道1的压力，内外取压口为前直管段同一截面的中分水平面两侧；前取压口在距流量计前端面2D（D为管道直径）的管道壁面上，后取压口距流量计后端面1D。前后取压口压差是本文要研究的压力损失。

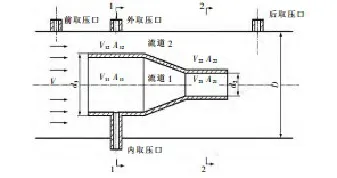
图1 内外管压差流量计结构示意图

（2）理论基础

与其他类型的压差式流量计相同，内外管压差流量计的工作原理同样是基于流体连续方程和伯努利方程。对于不可压缩流体，体积流量为

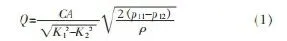
式中C——流出系数；

K1、K2——流道1和流道2的压缩比；

A——管道的截面积。

（3）影响压损的关键因素

根据内外管压差流量计的结构分析，忽略沿程压损，前后直管段长度适当取值；流量计形状参数中，梯形段倾角θ取流体与壁面即将分离的角度时压损最小，取θ=7°。为了消除大径、小径的具体数值对该流量计压损的影响，本文选用异径比k和等效直径比β进行试验研究。定义异径比为小径与大径之比，类比于孔板流量计和V锥流量计，定义内外管压差流量计的等效直径比β为通流面积与管道截面积的等效直径比。

式中R——管道半径；

r1——前直管段外圈半径；

r2——后直管段内圈半径（考虑流量计壁厚）。

通流面积是指在侧视图上看，不受节流件直接影响的流道面积，如图2所示，有剖面线部分为通流面积。

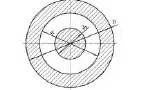
图2 管道侧视示意图

雷诺数是影响液压元件压损的一个重要因素，本文从异径比、等效直径比和雷诺数3个方面研究对内外管压差流量计的影响。

2 流量计的流场仿真

为方便参数化建模，本文采用UG进行三维实体建模，然后导入Fluent进行仿真。建模中管道内径为DN20的标准直径准27.2mm，流体采用常温水。

（1）建立模型

为了得出异径比和等效直径比β与压损之间的关系，在雷诺数Re相同的情况下，分别取β=0.9，0.85，0.8，0.7四组；在4组等效直径比下分别取k=0.3，0.4，0.5，0.6建立模型，共16组。为了解雷诺数Re与压损的关系，在相同等效直径比下，建立4组不同雷诺数模型，进行比较分析。由于所建模型较多，采用UG参数化建模，缩短三维建模时间。建立三维模型后，导入Fluent进行网格划分，本文中模型采用非结构四面体网格划分，图3为β=0.8，k=0.5的网格划分结果，有9521个节点，44115个单元。

图3 β=0.8，k=0.5模型网格划分结果图

（2）仿真设定与数据提取

本文所涉及的流动均为湍流流动，选择RNGk-ε湍流模型，亚松弛因子采用默认值，残差收敛精度设为1E-6。参数控制器设置中，压力选择2阶，其他为默认值。以进口速度进行初始化，进口速度设置中，选用湍流强度和水力直径进行设置，水力直径为管道直径，湍流强度

算法选用SIMPLE算法，迭代次数为2000次，进行计算。图4 为β=0.8，k=0.5模型、流速为1m/s下的压力云图。

图4 β=0.8，k=0.5模型压力云图

数据提取：前取压点为流量计前2D中心，后取压点为流量计后1D，内外取压点分别为流量计前直管段中段的内外侧。

3 仿真结果及数据分析

对于压差式流量计，压损一般分为永久压损和相对压损。永久压损是指流体由平稳流动流经流量计节流件后产生压差，再到平稳流动，在这个过程中因节流件产生的永久压力损失，本文的绝对压损为前后压差值；相对压损是指绝对压损与压差信号之比，本文定义压损比σ为内外管压差流量计的相对压损

仿真结果与数据如表1、表2、表3所示。

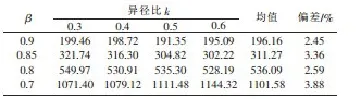
表1 相同Re、不同等效直径比β、不同异径比k时的绝对压损值/P

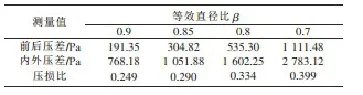
表2 相同Re、不同等效直径比β、异径比k=0.5时的相对压损

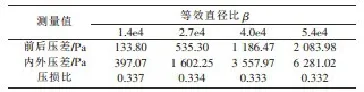
表3 不同Re、等效直径比β=0.8、异径比k=0.5时的相对压损

从表1中可以看到，在相同雷诺数、相同等效直径比、不同异径比的情况下，内外管压差流量计的永久压损值变化很小，最多不超过4%；而相同雷诺数、不同等效直径比，该流量计的永久压损值变化很大，随着等效直径比的减小而增大；从表2中可以看出相同雷诺数、相同异径比下，压损比随着等效直径比的减小而增大；从表3中可以得到在相同等效直径比、相同异径比下，永久压损值和信号值都随着雷诺数的增大而增大，且其增大的倍数约等于雷诺数增大倍数的二次方，但是压损比并没有随雷诺数增大而有明显变化。

4 流量计的流场模拟及结构优化

本文对流量计的结构优化主要是通过Gambit建模和Fluent仿真的，其中管径为50mm，仿真的流体介质为水。

4.1 模型的构建

由公式（3）知，当流量Q一定时，影响ΔP的参数主要有扩散角θ、异径管小径r和大径r＇。但当扩散角θ过小时，流体与壁面的接触面积会加大，导致压损增大；而当扩散角θ过大时，异径管内易出现流体与壁面分离的情况，形成漩涡区，增大压损。因此当扩散角θ为流体与壁面即将分离的角度时，压损最小。考虑到这一情况，本文选扩散角θ为7°，并选取r=10mm，r'=20mm；r=10mm，r'=30mm；r=10mm，r’=40mm；r=20mm，r’=30mm； r=20mm，r’=40mm；r=30mm，r’=40mm6种异径模型进行研究。为了方便，本文做如下定义：r=10mm，r’=20mm定义为管径r/r’=10/20，其他异径管大小管径也如此定义。本文中模型采用非结构四面体网格划分，图2是管径r/r＇=10/30的网格划分模型图，网格数量1.5万左右。

图5 管径比10/30的网格划分模型图

采用压力耦合方程组的半隐式算法（Semi-ImplicitMethodforP ressureLinkedEquations，简称SIMPLE算法），亚松弛因子采用默认值，残差收敛精度设为10-5。在选取湍流参数时，水力直径DH=50mm，湍流强度可由经验公式计算得到：

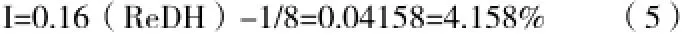
其中，ReDH为在流速1.0m/s时按水力直径计算得到的雷诺数。

4.3 Fluent仿真

对于一个差压传感装置而言，在干扰信号一定的情况下，传感器所接受的信号越大，所测得的结果越准确，因此异径管的内外差压越大越好。但是从节能角度来看，流体流经流量计所造成的压力损失应越小越好，因此流量计中轴线的前后两点的压差应越小越好。也就是说，异径管的内外差压越大，轴线的前后压差越小时，设计的内外管差压流量计的性能越优。结合这两情况，本文将异径管的内外压差

Δp内外和前后压差Δp前后的比值作为衡量该流量计的结构优劣的一个标准，该比值记为相对压损σ，即

当比值σ越大时，表示流量计的结构设计越优，反之σ越小，设计的流量计的综合性能越差。笔者在此做了管径r/r＇=10/20、10/30、10/40、20/30、20/40、30/40六个流量计模型，并在流速为1.0m/s的情况下进行仿真。

5 结语

综上所述，内外管压差流量计压损会很大程度上影响到流量计的工作，相关的工作人员对其进行科学的研究和分析有益于流量计的优化和设计工作达到较大的提升，因此必须引起重视。

［1］龙新平，王丰景，俞志君.喷射泵内部流动模拟与其扩散角优化［J］.核动力工程，2011，32（1）：53-57，69.

［2］吕玲，潘振.内锥流量计与孔板流量计的压力损失及能耗研究［J］.节能技术，2011，29（1）：45～48.