基于改进SSIM的HEVC率失真优化
班俊硕,赖惠成,林宪峰,杨 敏,董九玲
(新疆大学 信息科学与工程学院,新疆 乌鲁木齐 830046)

基于改进SSIM的HEVC率失真优化
班俊硕,赖惠成,林宪峰,杨敏,董九玲
(新疆大学 信息科学与工程学院,新疆 乌鲁木齐 830046)
HEVC继承了传统的客观率失真模型,主要采用均方误差、平方误差和或绝对误差和等客观评价方法作为失真测度。然而,这些方法并不能得到很好的主观视觉感知质量。为了进一步解决HEVC的计算复杂度,提出了将结构相似度(Structural Similarity,SSIM)引入到HEVC的率失真代价函数中。该方法使用失真测度均方误差对SSIM进行改进,将改进后的SSIM对率失真代价函数进行优化,求解出拉格朗日乘子,从而实现率失真性能的提升。实验结果表明,该方法与HEVC参考测试模型相比,在全I帧(All Intra,AI)配置下,率失真性能平均提高了2.6%,同时可以获得很好的编码质量,以及可忽略的编码时间增长。
高效视频编码(HEVC);率失真;结构相似度;拉格朗日乘子
H.265/HEVC(High Efficiency Video Coding)是由ITU-T视频编码专家组联合ISO/IEC运动图像专家组于2013年1月共同提出的下一代视频压缩标准。和上一代H.264/AVC视频压缩标准相比,在相同重建视频质量的条件下,降低大约50%的比特率,但是却大大提升了运算复杂度。和H.264的宏块编码方式相比,HEVC采用递归分块树形编码单元方式,编码单元最大尺寸为64×64,最小尺寸为8×8,而预测方向也从H.264的9种扩展到了35种[1]。这些在帧内预测等方面的改进在改善压缩性能的同时,也大幅增加了相应编码计算的复杂度。
视频压缩编码旨在降低码率的同时,尽可能满足对高视觉质量的追求,目前基于率失真优化(Rate Distortion Optimization,RDO)技术依然是视频编码中研究的热点。而HEVC中率失真优化技术依然采用传统的客观评价方法,如均方误差、平方误差和或绝对误差和等,这些方法都是客观上的失真准则,不能体现出主观质量。结构相似度(SSIM)计算复杂度低,符合人眼主观视觉特性,已被许多研究者引入到视频图像的失真度量中。Huang等[2]将SSIM应用到H.264的RDO中提出一种预测拉格朗日乘子的方法,采用1-SSIM改写失真度量函数,并划分关键帧和采用梯度下降法,从而求出拉格朗日乘子。Yeo等[3]对SSIM取倒数,结合SSE对RDO进行深度优化,在H.264/AVC上取得了比较好的效果。陈云善等[4]提出将SSIM加入代价函数,通过大量的实验得出经验参数。虽然该方法节省码率效果比较明显,但是由于是曲线拟合得到的经验公式需要大量实验才能得出数据,不适合视频内容变化比较大的场合和实时编码。Qi等[5]提出根据当前CTB(Coding Tree Block)和其相邻的CTBs分别从空间和时间上计算运动向量的方差,将两者进行合成并利用阈值选择出最佳值,同时结合SSIM求出的拉格朗日乘子对RDO进行优化。杨春玲等[6]在H.264帧内模式选择时首先找到SSIM和码率之间的近似关系,然后提出结合SSE作为失真测度的率失真代价优化方法。Rehman等[7]在前人研究的基础上将SSIM应用到DCT变换域,对SSIM指标分解为DC和AC残差系数,再对两者进行归一化,最后效率提高并不是很显著。朱天之等[8]根据HEVC编码树形结构使用SSIM计算失真度,得出码率、失真度和量化参数之间的关系,根据数学推导和统计分析,最终得到拉格朗日乘子。
综上所述,本文将SSIM作为失真度量引入到HEVC的RDO中,用失真测度MSE对SSIM进一步优化改进,最后将优化后的SSIM结合SSE共同作用于代价函数,求解出拉格朗日乘子。实验结果表明,本文所提方法能够在视频图像质量改善的情况下有效地提高编码效率和改善率失真性能。
1 率失真优化(RDO)
视频编码的主要目的就是在保证一定视频质量的条件下尽量减少编码比特率,或是在一定编码比特率限制条件下尽量地减小编码失真。基于率失真理论的编码参数优化方法被称为率失真优化,在视频编码中为保证编码器的编码效率通常采用率失真优化技术。HEVC视频编码率失真处理和H.264相似,同样采用传统的率失真优化,其RDO可以表示为
minDs.t.R≤RC
(1)
式中:D表示视频图像的编码失真;R表示视频图像编码需要的比特数;RC表示编码所允许的限定码率。该式为限定性约束问题,即在限定的码率下,使失真度达到最小值。
为了解决上述最小化问题,视频编码中通常的解决途径是采用拉格朗日优化方法。因此上述的限定性优化问题,通过引入拉格朗日乘子λ,可以转化为非约束性问题
minJ=D+λ×R
(2)
式中:J表示率失真代价;D表示视频图像的编码失真;λ表示拉格朗日乘子;R表示视频图像编码需要的比特数。所以视频编码的优化目标转化为最小化J。而λ为优化目标的调整因子,当λ有最优解时则J达到最小值。目前已有研究者提出直接根据限定码率预测出λ的取值,并应用到HEVC的码率控制算法中[9]。
2 结构相似度(SSIM)
结构相似度(SSIM)是Wang等[10]提出衡量两幅图像之间相似性的一种质量评价指标。传统的视频质量客观评价和失真测量都是基于误差求和的方法,而SSIM从亮度、对比度和结构信息3个方面综合考虑更符合人类视觉系统。SSIM的公式如下
SSIM(x,y)=l(x,y)·c(x,y)·s(x,y)=
(3)
式中:x和y表示要进行比较的两幅图像;l(x,y),c(x,y),s(x,y)分别表示亮度、对比度和结构信息;μx和μy分别表示x和y的均值;σx和σy分别表示两者的方差;σxy表示两者的协方差;而c1和c2是为了避免分母趋近0而导致不稳定设定的小常数。由文献[10]可知默认的c1=(k1L)2和c2=(k2L)2,其中k1=0.01,k2=0.03,L表示随图像变化的像素值,通常定义为L=2bitdepth-1。SSIM值的范围为:0≤SSIM(x,y)≤1。0表示两幅图像不相关,越接近于1表示两幅图像在主观质量上越相似。由于SSIM的低计算复杂度和更符合人类视觉感知系统,使其广泛用于编码视频的主观质量评价[11]。
3 基于SSIM的率失真优化
结合以上研究结果,本文将原始图像定为x,重建图像定义为y,则重建图像和原始图像的失真模型可以用式(4)表示
y=x+e
(4)
式中:e表示重建图像和原图像相比有损量化的失真值。则均方误差(MSE)可以用式(5)表示
(5)
式中:N是图像中像素的数量;yi表示重建图像中第i个元素所在图像块区域;xi表示原始图像中第i个元素所在图像块区域。为了利用MSE对SSIM进行优化,该式又可以被改写为
(6)
式中:σx和σy分别表示重建图像y和原始图像x的方差;μx和μy分别表示两者的均值;σxy表示两者的协方差。
很容易验证在高分辨率和大量数据下失真e的值通常很小,可以忽略不计。故原始图像x和重建图像y的均值有如下近似
μy≈μx
(7)
将式(6)、(7)代入式(3)可以获得SSIM的近似式
(8)
当图像的数据比较大时,又0≤SSIM(x,y)≤1,下面基于SSIM定义一个失真度量公式
(9)
式中:MSE为原始图像x和重建图像y的均方误差;σxy表示两者的协方差;c2为很小的常数。
当选择SSE作为失真测度时,率失真代价函数定义如下
JSSE=SSE+λSSE×R=N·MSE+λSSE×R
(10)
式中:SSE表示平方误差和;λSSE表示SSE作为失真测度时的拉格朗日乘子;N表示图像中像素的数量;MSE表示均方误差;R表示视频图像编码需要的比特数。
将SSIM引入RDO,式(10)可以被改写为
(11)
则优化目标转化为
J=DSSE+(2σxy+c2)·λSSIM×R
(12)
式中:DSSE表示当SSE作为失真测度时的编码失真;σxy表示协方差;c2为小常数;R为视频图像编码需要的比特数。为确定λSSIM,本文需要引入率失真模型。目前率失真在视频编码中采用的都是对数模型[12],对于一帧视频图像的每个编码块有式(13)
(13)
式中:α是一个比例常数;σ2表示编码位移帧差(DFD)。对式(12)用拉格朗日乘数法求解λSSIM的最优值,得到
(14)
(15)
根据式(11)、(14)和(15)可以得出率失真优化拉格朗日乘子
(16)
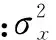
4 实验结果及分析
为了验证本文算法的效果,采用官方给出的HEVC参考测试模型HM13.0[14]进行测试分析,所有不同分辨率的测试视频序列均来自标准测试视频序列。对HM13.0的配置[15]为:全I帧编码;测试的量化参数设置为固定QP;CTU的最大尺寸为64×64、深度为4。实验结果如表1所示,采用BD-PSNR和BD-SSIM来衡量本文算法的率失真性能,ΔT表示编码时间。
表1本文算法与HM测试模型对比结果
%
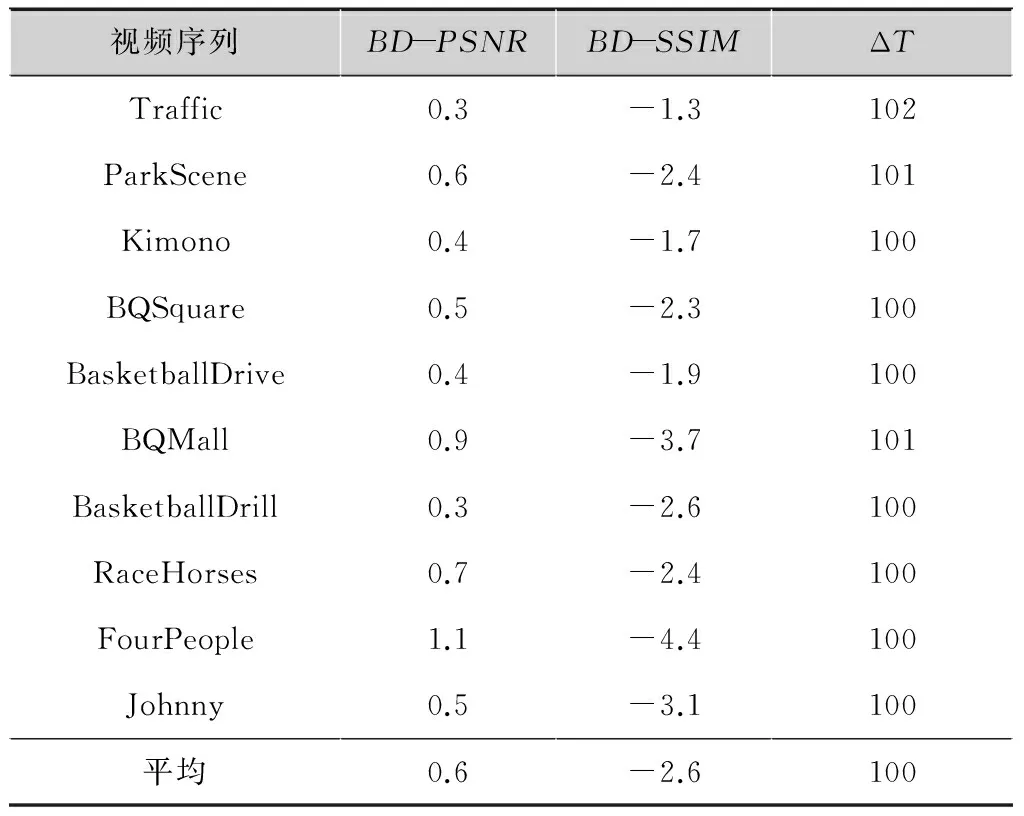
视频序列BD-PSNRBD-SSIMΔTTraffic0.3-1.3102ParkScene0.6-2.4101Kimono0.4-1.7100BQSquare0.5-2.3100BasketballDrive0.4-1.9100BQMall0.9-3.7101BasketballDrill0.3-2.6100RaceHorses0.7-2.4100FourPeople1.1-4.4100Johnny0.5-3.1100平均0.6-2.6100
从表1可以看出,本文所提算法的率失真性能提升最高为4.4%,最低为1.3%,平均增加了2.6%,同时BD-PSNR只有很小的损失。其中Traffic序列由于车辆在移动,导致运动相对剧烈,同时整帧的纹理也比较复杂,因而其率失真性能最差。而FourPeople序列运动相对平缓,纹理相对简单,所以率失真性能最好。本文算法对于所有测试序列HEVC的编码时间只有个别微小的增长,平均编码时间的增长是可以忽略的。
以HM13.0作为对比,图1给出了BQSquare和Johnny两个序列的率失真曲线图。从图中的曲线可以看出本文提出算法的率失真性能优于HM13.0。

图1 本文算法和HM测试模型率失真性能比较
5 结束语
针对HEVC中客观的率失真优化准则不能够得到最佳视频图像主观感知质量的问题,同时为提升率失真性能,本文提出一种基于改进SSIM的HEVC率失真优化算法。该方法利用失真测度均方误差(MSE)对SSIM进行改进,将改进后的SSIM对率失真代价函数进行优化,求解出拉格朗日乘子。实验结果表明,本文算法能够改善视频主观质量,提高编码效率,同时率失真性能平均增加了2.6%。下一步的研究重点是继续深入研究本文算法将其应用到HEVC模式选择和帧间编码RDO中,进一步提高HEVC的编码质量和编码效率。
[1]SULLIVAN G J, OHM J, HAN W J, et al. Overview of the High Efficiency Video Coding (HEVC) standard[J].IEEE transactions on circuits & systems for video technology,2012,22(12):1649-1668.
[2]HUANG Y H, OU T S, SU P Y, et al. Perceptual rate-distortion optimization using structural similarity index as quality metric[J].IEEE transactions on circuits & systems for video technology,2010,20(11):1614-1624.
[3]YEO C, TAN H L, TAN Y H. On rate distortion optimization using SSIM[J].IEEE transactions on circuits & systems for video technology, 2013, 23(7):1170-1181.
[4]陈云善,高慧斌,苏宛新,等.结构相似度在AVS帧间模式选择中的应用[J].光电子·激光,2011(3):435-439.
[5]QI J,LI X,SU F,et al. Efficient rate-distortion optimization for HEVC using SSIM and motion homogeneity[C]//Proc. 2013 Picture Coding Symposium (PCS).[S.l.]:IEEE,2013: 217-220.
[6]杨春玲,肖冬琴.基于SSE和SSIM的H.264帧内预测模式选择改进算法[J].电子与信息学报,2011(2):289-294.
[7]REHMAN A, WANG Z.SSIM-inspired perceptual video coding for HEVC[C]//Proc. IEEE International Conference on Multimedia and Expo. Melbourne: IEEE Computer Society, 2012:497-502.
[8]朱天之,郁梅,蒋刚毅,等.基于SSIM的HEVC帧内编码率失真优化[J].光电子·激光,2014(12):2362-2370.
[9]LI B,LI H,LI L, et al. Rate control by R-lambda model for HEVC[C]//Proc. Joint Collaborative Team on Video Coding (JCT-VC) of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 11th Meeting. Shanghai:ITU, 2012:10-19.
[10]WANG Z, ALAN C B, HAMID R S, et al. Image quality assessment: from error visibility to structural similarity[J].IEEE transactions on image processing,2004,13(4):600-612.
[11]张玮,宋利,杨小康.基于视频编码增益的视频质量评价算法性能研究[J].电视技术,2014,38(15): 44- 48.
[12]SULLIVAN G J, WIEGAND T. Rate-distortion optimization for video compression[J].Signal processing magazine,1998,15(6):74-90.
[13]WIEGAND T, SCHWARZ H, JOCH A, et al. Rate-constrained coder control and comparison of video coding standards[J].IEEE transactions on circuits & systems for video technology,2003, 13(7):688-703.
[14]MCCANN K, BROSS B, SUGIMOTO K, et al. High Efficiency Video Coding(HEVC)test model 13(HM13)encoder description[C]//Proc. Joint Collaborative Team on Video Coding (JCT-VC) of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11 15th Meeting. Geneva, Switzerland:ITU,2013:1-39.
[15]BOSSEN F. Common test conditions and software reference configurations[C]//Proc. Joint Collaborative Team on Video Coding (JCT-VC) of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11 12th Meeting. Geneva, Switzerland: ITU,2013:1-4.
班俊硕(1988— ),硕士生,主要研究方向为视频编码;
赖惠成(1963— ),教授,主要研究方向为图像处理及视频信号编解码等;
林宪峰(1990— ),硕士生,主要研究方向为视频质量评价;
杨敏(1990— ),硕士生,主要研究方向为图像处理;
董九玲(1986— ),女,硕士生,主要研究方向为图像处理。
责任编辑:时雯
Rate distortion optimization based on improved SSIM for HEVC
BAN Junshuo,LAI Huicheng,LIN Xianfeng,YANG Min,DONG Jiuling
(CollegeofInformationScienceandEngineering,XinjiangUniversity,Urumqi830046,China)
Objective appraisal method, such as mean square error(MSE), sum of the squared errors(SSE)or sum of absolute difference(SAD), is adopted by HEVC, which inherits conventional objective rate distortion model. However, these methods fail to achieve high consistency with subjective visual perception. In order to reduce the computational complexity of HEVC, in this paper, SSIM is considered as rate distortion cost function of HEVC. MSE is introduced into SSIM, so that a new rate distortion cost function can get. This problem can be solved by Lagrangian multiplier method. Experimental results show that compared our proposed algorithm with HM13.0 in AI configuration, the performance of rate distortion is average improved about 2.6%, as well as getting better coding quality. In addition, no significant runtime increases in the encoding process.
HEVC; rate distortion; structural similarity; lagrange multiplier
TN919.8
ADOI:10.16280/j.videoe.2016.07.003
国家自然科学基金项目(61561048);新疆维吾尔自治区科学基金项目(2015211C257)
2016-01-28
文献引用格式:班俊硕,赖惠成,林宪峰,等.基于改进SSIM的HEVC率失真优化[J].电视技术,2016,40(7):11-14.
BAN J S,LAI H C,LIN X F,et al.Rate distortion optimization based on improved SSIM for HEVC[J].Video engineering,2016,40(7):11-14.

