基于多体系统理论的榫卯加工中心夹具系统精度建模分析*

刘志峰，赵林忠，李　迎，孙光辉，马　雷

(北京工业大学 机械工程与应用电子技术学院，北京　100124)



基于多体系统理论的榫卯加工中心夹具系统精度建模分析*

刘志峰，赵林忠，李迎，孙光辉，马雷

(北京工业大学 机械工程与应用电子技术学院，北京100124)

针对榫卯加工中心加工过程中出现加工误差大的现象，分析造成误差的主要误差源是夹具系统。榫卯加工中心的夹具系统采用螺栓定位，较大影响了整个夹具系统的装配精度，对整体加工造成较大的加工误差。根据该夹具系统的机械结构及其连接方式，提出基于多体系统运动学理论和齐次变换的方法，建立榫卯加工中心夹具系统的误差模型，并推导了考虑装配误差的最终误差公式。针对运用螺栓定位造成的加工缺陷，并考虑夹具系统的特殊性，提出了一种夹具系统改进方案，并利用多体系统运动学理论建立误差模型，为提高榫卯加工中心加工精度提供理论依据。

夹具系统；装配精度；多体系统；齐次变换；误差模型

0　引言

数控机床中的夹具系统对整个机床整体的加工精度有着重要的影响，其中工作台作为夹具系统的关键部位，其工作精度和装配精度对夹具系统有着较大的影响。因此对其精度设计是非常有必要的，也是优化设计的重要环节。

对夹具系统进行精度设计需建立其误差模型，本文主要进行对夹具系统中部件装配时产生的空间几何误差分析，不考虑其受热变形及受力变形所产生的误差。在机械结构空间误差建模方面，世界各国专家学者经过多年研究已经发展出误差矩阵法、机构学建模法、刚体运动学等多种建模方法[1]，而多体系统理论是对一般复杂机械系统的完整抽象和有效描述，是分析和研究复杂机械系统的最优模式[2]，目前已经在机器人，机床，坐标测量机等复杂机械的运动分析与控制中得到成功应用，并且应用领域正在不断扩大[3]。刘又午等人[4]已经曾利用多体系统理论对机床建模进行了系统性的研究，并且已经取得了很多成果。在回转工作台精度分析方面，主要还是以传统建模方法为主。精度分配的方法主要有尺寸链理论法[5]、蒙特卡洛法[6]等。此外王禹林等人[7]为螺杆转子磨床精度分配建立了一种多目标参数化模型，这些工作都将为夹具系统精度建模分析提供有益的帮助。

基于多体系统理论[8]建立的木工机床夹具系统误差模型，能够描述夹具系统中各个组成部分在装配时由于部件制造精度以及它们之间的约束方式造成的误差是怎么通过结构关系以及相对运动转化成最终整体的定位误差，由此可以定量分析出各类基本误差对整体加工误差的影响情况，从而为夹具系统的精度建模和设计优化提供依据。

1　拓扑结构和低序体阵列

多体系统误差建模方法是将工程对象抽象为多体系统[9]，用低序体阵列来描述拓扑结构中各体之间的关联，在多体系统中建立广义坐标系，在坐标系中采用4×4阶齐次特征矩阵运算表示点和矢量在坐标系中的位置和姿态的变换，而拓扑结构是对多体系统本质的高度提炼和概括，是研究多体系统的依据和基础。罗伯森和威腾伯格提出的基于图论和休斯顿和刘又午的运用低序体阵列描述多体系统拓扑结构的两种基本方法，其中，低序体阵列是通过多体系统拓扑结构更为简洁方便，适合于计算机自动描述多体系统，本文采用的是拓扑结构的低序体阵列描述法。

本文所研究的夹具系统，它是一种专为木工机械开发的夹具，具有高稳定性、高刚度、高速度等特点，适合用于木工加工。该夹具系统主要是由溜板、转台座、转台、台面、夹具体1、夹具体2以及工件组成。对图1所示的夹具系统进行提炼和概括，就可得到如图2所示的拓扑结构简图。

对图1的夹具系统进行简述如下：0—溜板,1—转台座,2—转台,3—台面,4—夹具体1,5—夹具体2,6—工件。坐标系设置如下：①在溜板和所部件上，建立笛卡尔坐标系；②系统各元素X、Y分别平行，Z轴同轴。

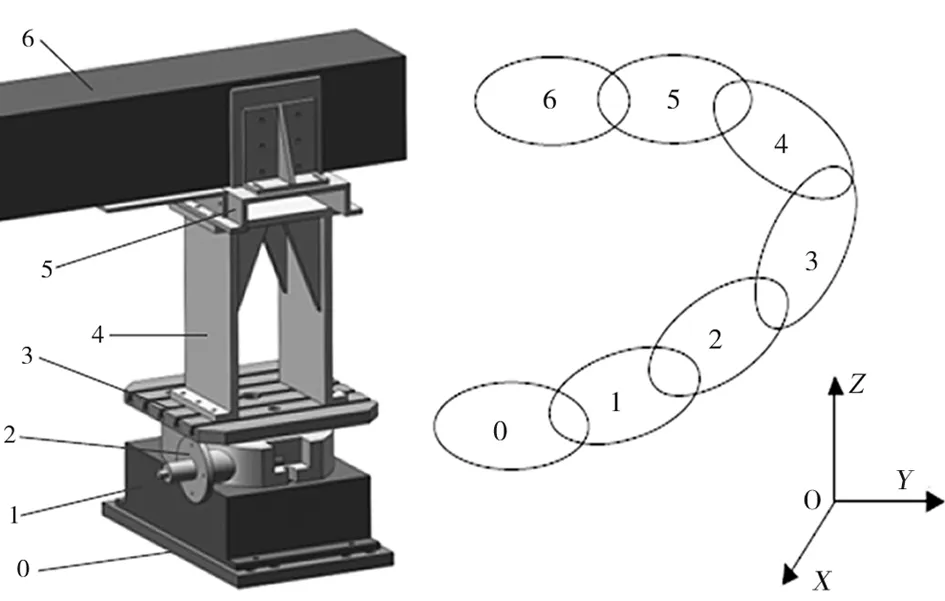
图1　夹具系统结构简图　　　图2　拓扑结构图

在多体系统分析中，我们把构成拓扑结构的单元称为体，描述体与体关联关系的低序体阵列可通过下列定义的低序体运算得到。一般的在多体系统中对任意体(V)的低序定义如下：

Ln(V)=S

(1)

Ln(V)=L[Ln-1(v)]

(2)

Lo(V)=V

(3)

Lo(0)=0

(4)

当Ln(V)=S时称体S是v的相邻低序体，同时称V是s的相邻高序体。

以图2所示的多体系统拓扑结构为例，根据上述低序体运算公式可以求出各体的各阶低序体号，从而构成表1所示的低序体阵列，它即是夹具系统的低序体阵列。

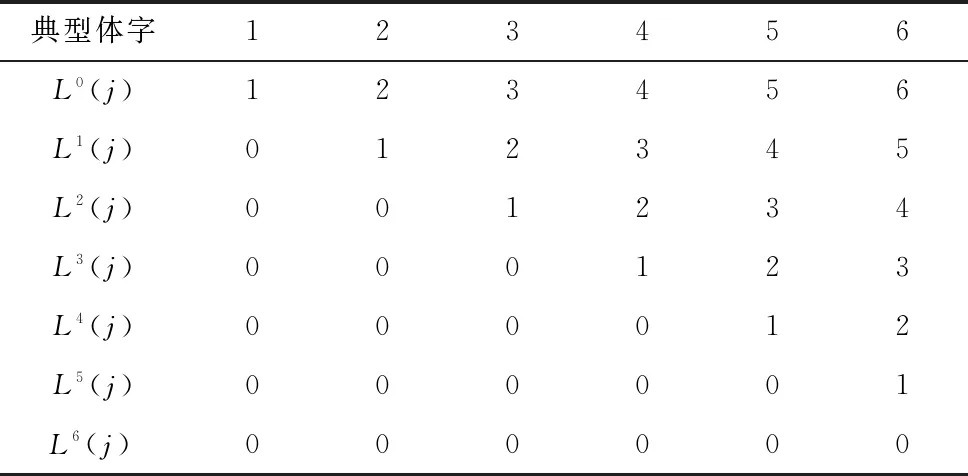
表1　夹具系统多体拓扑结构的低序阵列

2　特征矩阵

多体系统中各体之间的位置和运动关系，用相应的坐标系的位置和姿态变换来确定。根据子坐标系的位姿参数,可以得到各种确定的4×4阶齐次特征矩阵,而参数的变化与否反映了体与体之间的相对静止和相对运动状况。

在有误差的多体系统中，对于任意相邻体S、V的子坐标系,相对静止(或初始相对静止)的理想静止特征矩阵[10]为:

(5)

相对静止的静止误差特征矩阵为：

(6)

相对运动的理想运动特征矩阵为:

(7)

相对运动的运动误差特征矩阵为:

(8)

式(5)～式(8)中,aSV、bSV、cSV为坐标系V、S原点之间的静止位置,αSV、βSV、γSV为坐标系V、S坐标架之间的静止姿态,xSV、ySV、zSV为坐标系V、S原点之间的相对平移运动量,θxSV、θySV、θzSV分别为坐标系V绕坐标系S的X、Y、Z轴的回转运动角。

对本夹具系统的结构进行分析可知：在夹具系统中各部件之间除组件2和组件3之间有旋转关系，其余部件都是由螺钉连接，不可避免的在装配时会出现误差。由此根据加工中心的结构、各部件之间的运动关系，建立各相邻近体间的变换特征矩阵如表2所示。

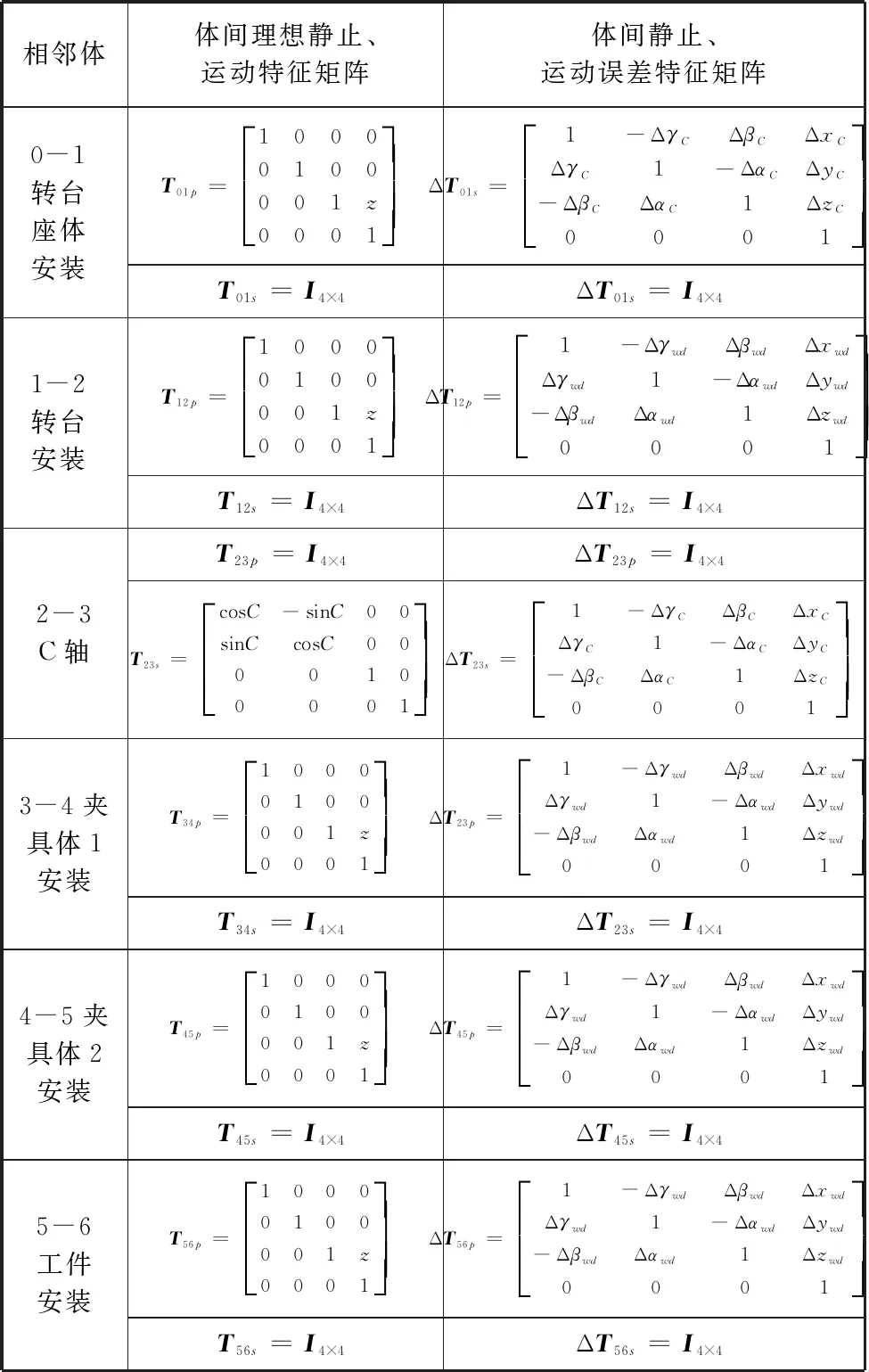
表2　夹具系统的特征方程

3　夹具系统误差模型建立

设刀具成形点在刀具坐标系内的坐标为：

(9)

工件上成形点在工件坐标系中的坐标为：

(10)

理想运动情况下有：

(11)

故夹具系统在无误差情况(理想情况)下，刀具成形点在工件坐标系内的理想成行函数为：

(12)

然而在实际装配过程中，不可避免会出现误差从而形成空间误差，夹具系统的实际成形点与理想刀具成形点的综合空间位置误差为式如下：

(13)

4　夹具系统误差分析

本文研究的夹具系统固定采用M8螺钉固定。但螺栓不能起到联接作用，不能用于定位。若两个零件只是平面对接，没有销、孔联接的时候，体之间的装配误差主要由螺钉联接产生。

参照GB5277-85紧固件、螺栓和螺钉通孔的标准,通孔公差有以下规定精装配系列：H12；中等装配系列：H13；粗装配系列：H14。在选择参数过程中，使用通孔公差H12，并根据零件加工图纸中的形位公差确定各环节的转误差。具体标准如表3所示。

表3　紧固件、螺栓和螺钉通孔标准

根据夹具零件加工尺寸公差及形位公差可以计算夹具系统的几何误差参数如表4所示。

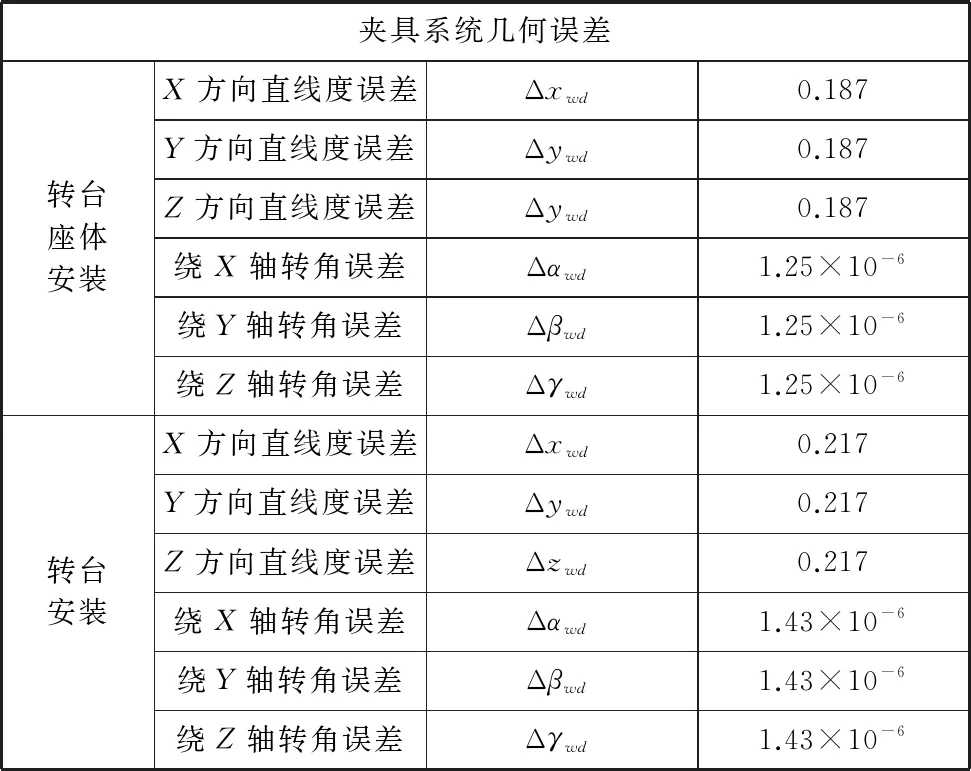
表4　夹具的几何误差

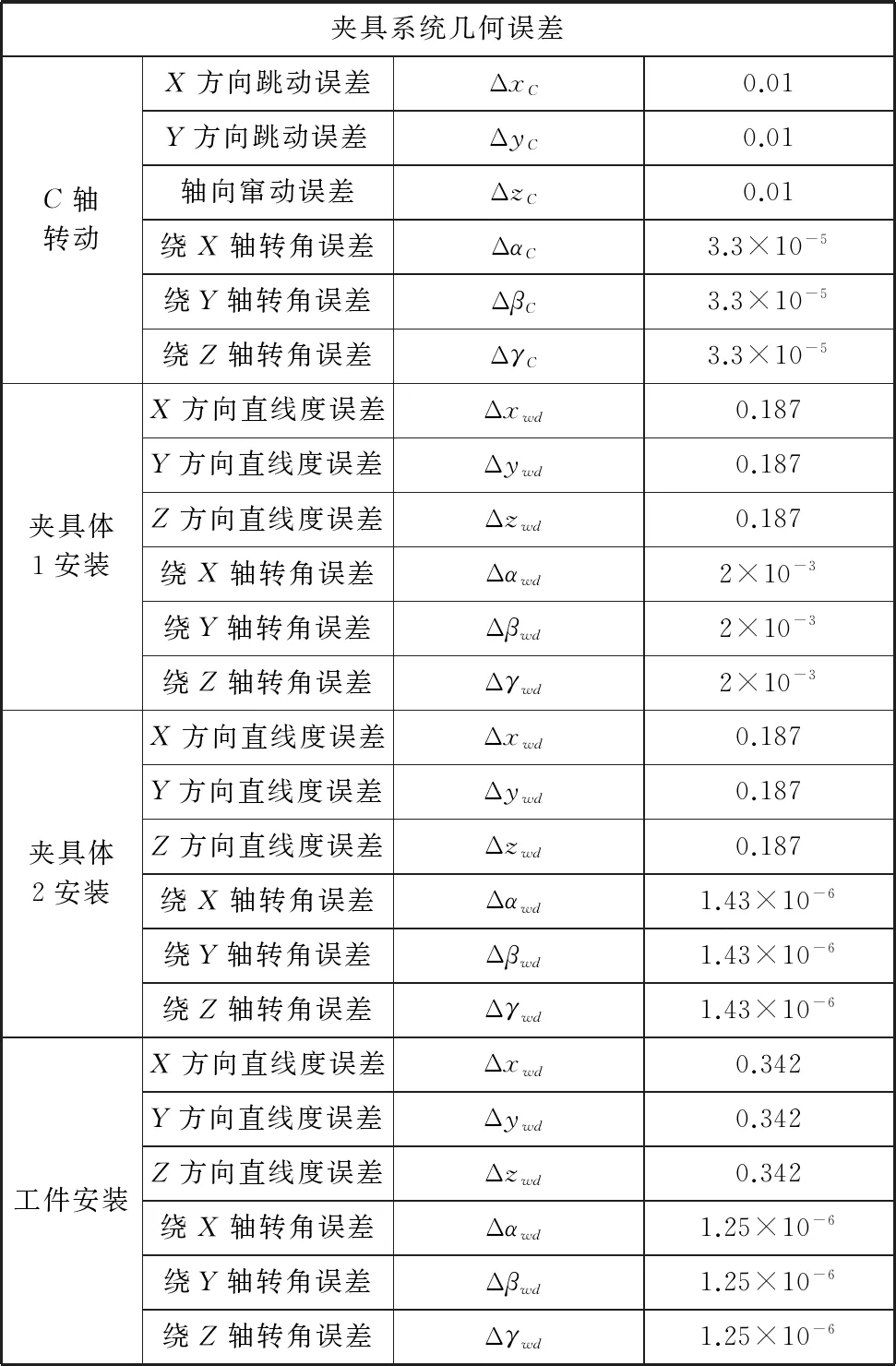
续表

将以上数据带入式(13)中得到如下：

E=

式中Pw工件在工件坐标系中的齐次坐标系，在夹具上安装距回转中心300mm的试件，在转台0°和90°的位置用铣刀沿回转中心对称向加工两个方形槽，两个方向方形槽相交打透,当考虑工件坐标系误差单一因素时，工件坐标系原点在机床坐标系中的产生的误差由以上设定的值，可得的取值范围：

Δx=[-0.322,1.03]，Δy=[-0.322,1.03]，Δz=[0,1.13]

如果加工程序按照理想状态下工件坐标系的情况加工，加工后的工件会出现极大的台阶，不能满足木工加工精度0.5mm的要求。

5　夹具系统结构改进

经理论计算发现现有的夹具系统不能满足加工要求，对夹具系统结构进行如下改造：简化夹具体结构堆积层数，将夹具体直接在转台上加装夹具体，止口定位；夹具体上方直接通过键定位，安装虎口钳；虎口钳属于精度较高并且具有自定心功能，尽可能的减小装夹误差；夹具体采用圆筒形结构，增加刚度。

改造后的夹具系统如图3所示，对图3所示的夹具系统进行提炼和概括，就可得到如图4所示的拓扑结构简图。

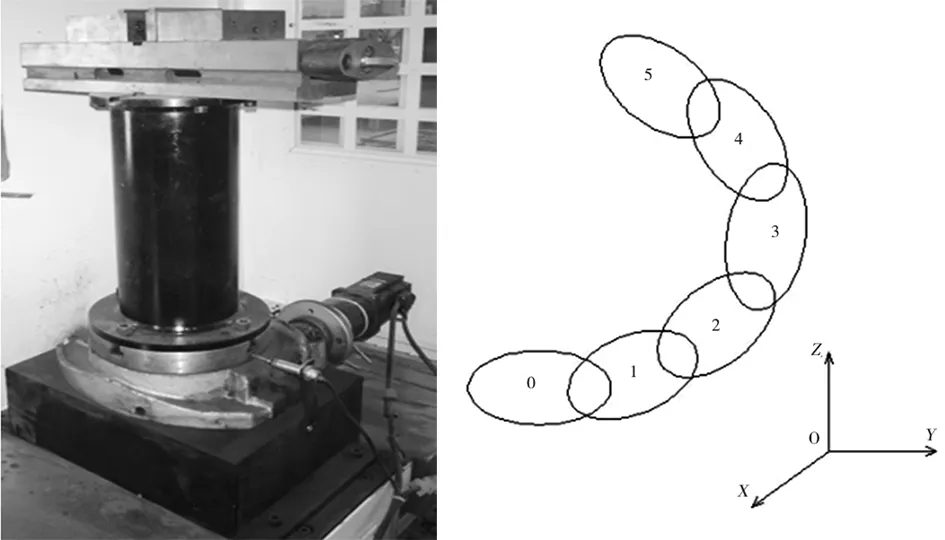
图3　夹具系统改造后　　图4　拓扑结构图

针对图4的夹具系统的拓扑结构简述：0—溜板，1—转台座，2—转台，3—夹具体，4—夹具体2，5—工件。改进后的夹具系统的空间误差公式如下所示：

T01PΔT01PT12PΔT12PT23SΔT23ST34PΔT34PT45PΔT45P=

(14)

改进后的夹具系统对于转台和夹具体之间的联接改用键定位，并通过查阅键与槽公差配合等相关资料可得几何误差尺寸如表5所示。

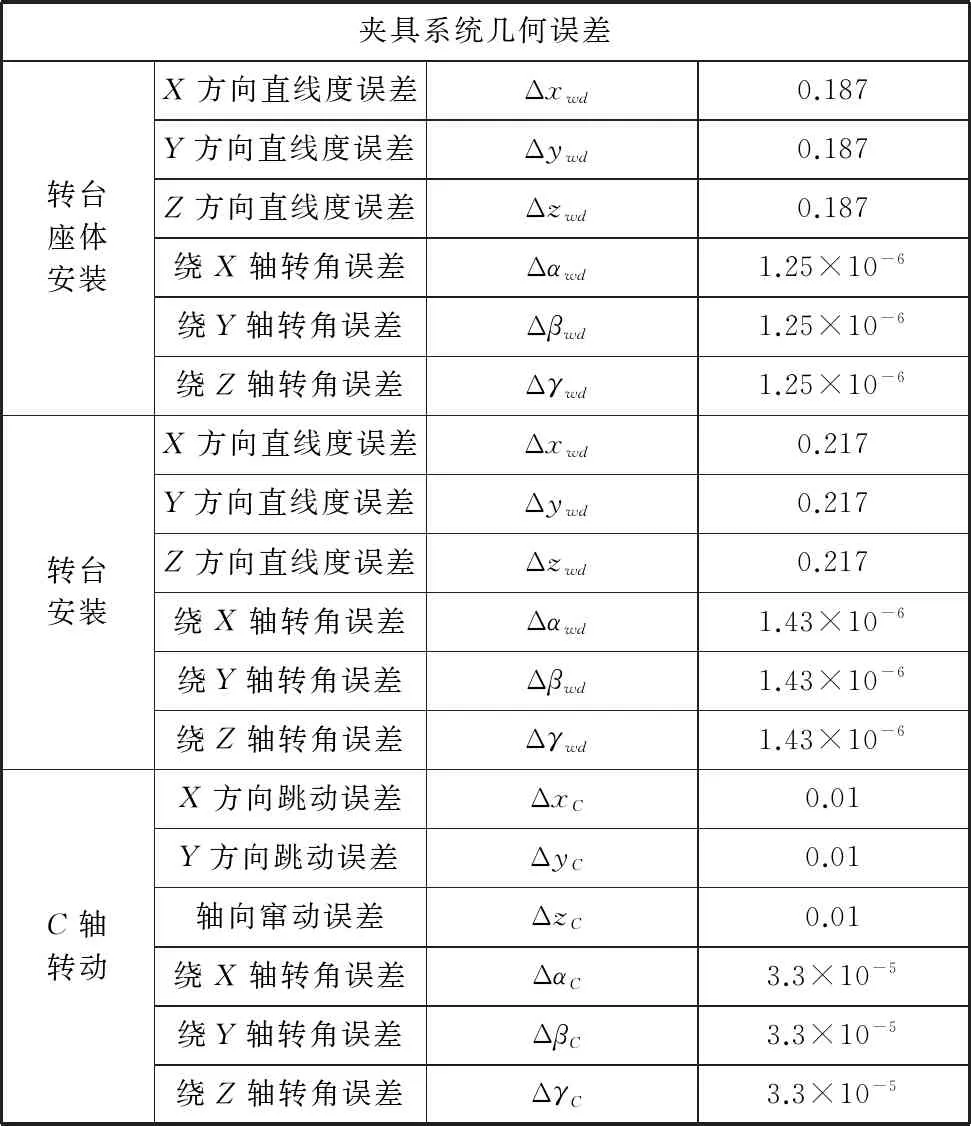
表5　改造后夹具的几何误差

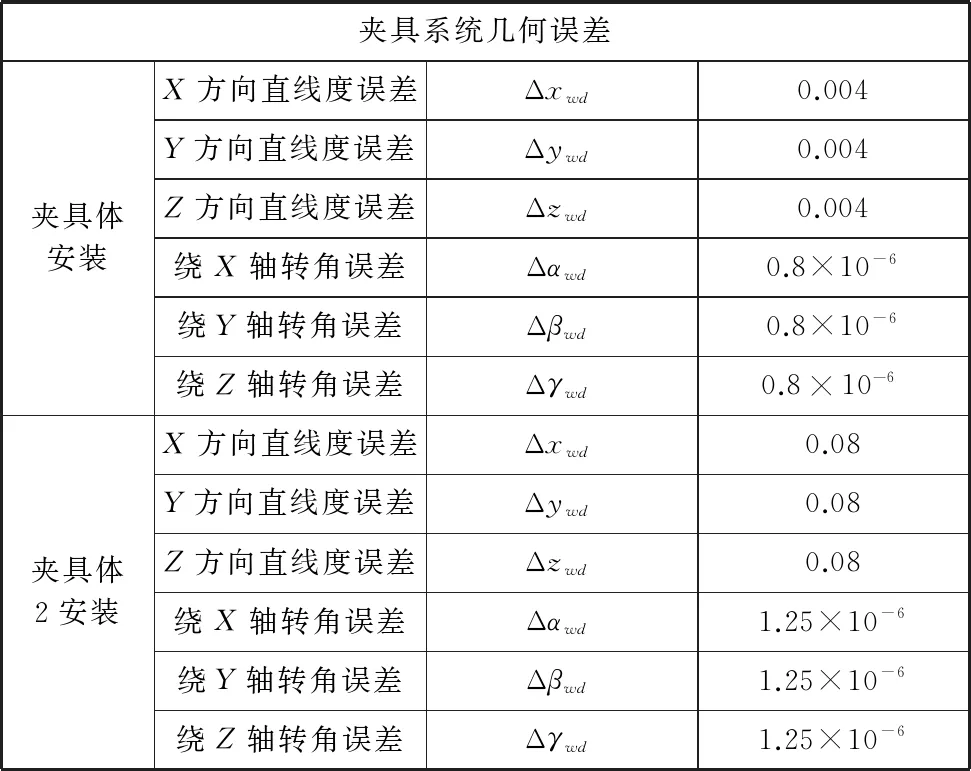
续表

将以上数据带入式(14)中得到如下：

按着在转台0°和90°的位置这2个位置测试，用铣刀沿回转中心对称向加工两个方形槽，两个方向方形槽相交打透,当考虑工件坐标系误差单一因素时，可得在工件坐标系中工件坐标原点的误差取值范围如下：

Δx=[0.391,0.498]，Δy=[0,0.498]，Δz=[0,0.498]

由此可以看出，经过改进后的夹具系统基本上满足木工加工精度0.5mm的要求。

6　结束语

针对榫卯数控加工中心的夹具系统利用螺栓定位造成的加工误差，利用多体系统运动学理论来构建榫卯加工中心夹具系统误差模型，并通过理论分析，可以看出：①该方法简单、明确，具有广泛的通用性；②该方法的相邻低序体之间的特征矩阵的形成具有很好的规律性，能够简单明确的描述机械系统，并对夹具系统进行误差建模分析；③螺栓只能用于两物体之间的连接，在夹具体系统中利用螺栓定位，会给加工造成比较大的误差；④改变具体结构堆积层数，并改变定位方式，能较大的减少夹具系统的误差，达到加工效果；⑤本文中的夹具系统的转台为外购件，提高转台本身的精度，对整个夹具系统精度的提高有着重要的影响。

[1] 粟时平，李圣怡，王贵林.基于空间误差模型的加工中心几何误差辨识方法[J].机械工程学报,2002,38(7):121-125.

[2] 刘又午.多体动力学在机械工程领域的应用[J].中国机械工程，2000,11(1-2):144-149.

[3] 郭辰，杨林，李庆勇.基于多体系统理论的数控机床误差建模[J].机械设计与制造,2005(3):123-125.

[4] 刘丽冰，王广彦，刘又午.复杂机械系统运动误差自动建模技术研究[J].中国机械工程,2000,11(6):642-646.

[5] 赵学满，倪雁冰，徐淑静.并联机床关键零部件精度设计[J].机床与液压,2004(5):58,55.

[6] 卢强，张友良.用蒙特卡洛法进行6腿并联机床精度综合[J].中国机械工程,2002,13(6):464-467.

[7] 王禹林，陶丽佳，孙文钊,等.基于多体系统理论的螺杆转子磨床精度分析与优化[J].南京理工大学学报,2012，36(6):1015-1020.

[8] 贾时平，李圣怡.五轴数控机床综合空间误差的多体系统运动学建模[J].组合机床与自动化加工技术，2003(5):15-18，21.

[9] 刘又午，刘丽冰，赵小松，等.数控机床误差补偿技术研究[J].中国机械工程，1998,9(12):48-52.

[10] Su Shiping, Li Shengyi.A study on Prediction Modeling of Machining Accuracy for CNC Machine Tools[J].ICPN′2002,2002,2(10):123-127.

(编辑李秀敏)

Precision Modeling and Analysis of Fixture System of Tenon Machining Center Based on Theory of Multi-body System

LIU Zhi-feng，ZHAO Lin-zhong，LI Ying，SUN Guang-hui，MA Lei

(College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing 100124，China)

According to the appearance that the machining error of tenon machining center which is produced during working process, the main error source of the analysis is the fixture system.The fixture system of tenon machining center uses the bolt positioning,which affects the assembly accuracy of the whole fixture system,and results in a large machining error. In order to derive the error formula of the assembly model and establish the error model of the fixture system, according to the mechanical structure and the connection mode,proposing the method which is based on multi-body system kinematics theory and homogeneous translation.According to the use of bolt positioning which causes fault during working process and considering the particularity of the fixture system,proposing a method that improves scheme of the fixture system for improving the machining accuracy of tenon machining center,and establishes error model which is used multi-body system kinematics theory.

fixture system;assembly accuracy;multi-body system;homogeneous translation;error model

1001-2265(2016)07-0122-05DOI:10.13462/j.cnki.mmtamt.2016.07.035

2015-09-06

863项目(SS2012AA040704)；北京工业大学京华人才支持项目

刘志峰(1973—),男，辽宁辽阳人，北京工业大学教授，研究方向为CAE，机械传动，精密加工，(E-mail)lzf@bjut.edu.cn。

TH166;TG659

A