改进的深度信念网在磨削加工粗糙度值预测中的应用*
田 杨
(辽宁工程职业学院 科研处,辽宁 铁岭 112000)
改进的深度信念网在磨削加工粗糙度值预测中的应用*
田杨
(辽宁工程职业学院 科研处,辽宁 铁岭112000)
深度信念网(DBN)是由无监督的受限玻尔兹曼机(RBM)和有监督的BP网络组成的神经网络分类器。针对RBM训练过程中固定学习率不利于寻找最优的缺点,提出一种动态学习率法则,改进RBM网络以提高特征向量映射的准确度;构造一个含有两层RBM和一层BP,并使用对比分散准则(CD准则)进行神经网络的自训练的DBN网络,提高训练速度,将改进型网络应用于表面粗糙度值的预测,通过与改进前后的预测模型及RBM预测模型的对比,预测模型精度得到了提高。
深度信念网;RBM;粗糙度;预测模型
0 引言
表面粗糙度是评价工件表面质量的重要因素之一,他对工件的疲劳强度、接触刚度、配合性能、工作精度都有着重要的影响,然而由于不同加工参数的选择,加工表面的粗糙度值也随之改变,为此需要建立一种根据加工参数即可确定粗糙度值的预测模型,国内外学者针对粗糙度预测模型做了相应的研究,王洪详等[1]采用回归分析法建立单点金刚石刀具超精车削表面粗糙度预测模型,苏宇等[2]采用自适应神经模糊推理系统建立了铝合金铣削加工表面粗糙度预测模型;周斌等[3]建立了基于BP神经网络的表面粗糙度预测模型;刘牧等[4]采用响应曲面法建立了钢及其合金铣削加工表面粗糙度预测模型;陈杰来等[5]采用遗传算法优化的反向神经网络法建立了超精密切削表面粗糙度预测模型;刘晓志等[6]利用线性回归分析方法建立了硬质合金立刀铣削钛合金才来的表面粗糙度模型。
由于神经网络法在泛化能力方面尚存在不足、训练时间长、难以表达结构化知识等缺点,本文提出一种动态学习率策略来训练RBM网络,该方法通过在训练过程中逐渐调整学习率,克服了固定学习率引起的特征提取精度不高的问题,提高RBM和DBN的特征向量映射能力,将该模型应用于磨削表面粗糙度值的预测中,可满足粗糙度模型的预测精度。
1 深度信念网(DBN)
深度信念网(Deep Belief Networks,DBN)由一系列叠加的受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)和一层BP网络构成,其结构如图1所示。DBN的训练过程可以分为两步:首先,使用无监督学习方法训练每一层RBM,且每个RBM的输入为上一个RBM的输出,即每一层RBM都要单独训练,确保特征向量映射到不同的特征空间时,尽可能多的保留特征信息;第二,使用最后一层的BP网络接收最后一个RBM的输出,用有监督的方式训练整个网络,对其进行微调。

图1 DBN网络结构
在第一步中,对每一层RBM的训练能确保本RBM层内的权值对特征向量的映射达到最优,而不能保证整个DBN是最优的,因为其不能完全消除映射过程中产生的错误和不重要的信息,而多个RBM会逐渐弱化上一层网络产生的错误和次要信息,该过程可以看成对最后一层的BP进行参数初始化,能有效避免BP网络因随机初始化的参数造成容易陷入局部极小和训练时间过长的缺点。而使用第二步的反向传播网络能够将某些需要调整的信息自上而下传播给每一个RBM,进而整个DBN网络,已经证明在BP网络之前,整个网络的效果已经比较好[7-8],因此BP的作用是对整个DBN进行微调。
在DBN训练过程中,底层的网络接收原始数据的特征向量,自下而上的传递,每一层提取数据的一个或多个方面的特征,并把提取的特征作为下一层的输入,在上层网络中形成更易分类的组合特征向量,因此DBN是一个含有多隐含层的深度架构的神经网络。文献[9]证明增加网络中RBM的个数仍然能够保证整个DBN网络的稳定,且RBM个数越多,能够使特征向量更加抽象化,用于数据分类的训练结果也更精确,但一般来讲使用3个RBM的结果已经足够精确[11]。
RBM是DBN的重要组成部分,也是整个网络的核心,它由一个可见层和一个隐含层组成,可视层作为输入部分,同时也是反向传播的输出部分,可视层与隐含层之间使用双向全连接,学习规则采用模拟退火算法,层与层之间进行双向全连接,但同一层内没有连接。
公式(1)为由已知的可视层节点得到的隐含层节点的值:
(1)
由于RBM是对称网络,因此可以得到由隐含层节点得到可视层节点的值,见公式(2):
(2)
式中,vi是可视层第个节点的值,hj是隐含层第个节点的值,b和c分别表示可视层和隐含层的偏置值,wij为可视节点i和隐藏节点j之间的权值。
公式(3)为可视层的特征向量和隐含层的特征向量的联合概率分布:
p(v,h)∝exp(-E(v,h))=ehTwv+bTv+cTh
(3)

(4)
式中,τ为迭代次数,η为学习速度。τ可以根据网络规模进行设置τ=100~2000,学习速率能够影响网络的学习进度,合适的学习速率是保证θ=(W,b,c)学习到最佳状态的必要条件。在RBM训练过程中,运算初期在大范围内调整,而到迭代后期,网络基本趋于稳定,只需要部分且小步的调整,因此传统的固定长度的学习速率η不适用于迭代寻优,因此本实验通过设定一个学习系数μ来动态调整学习速率,学习率调整公示如下:
ηt=μηmax+(1-μ)ηmin
(5)
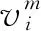
(6)
式中,
(7)
实际上,由于难以确定步长,利用马尔科夫链的方法求得的P(v,h)和末端的联合概率分布P(vi∞,hj∞)难以保证收敛性,因此实验中可以使用Contrastive Divergence准则(CD准则)[11]来提高计算速度和保证计算精度。CD准则公式如下所示:
CDn=KL(p0‖p∞)-KL(pn‖p∞)
(8)
式中,p0为RBM在t=0时刻(即初始状态)的联合概率分布,pn为经过n步马尔科夫链的计算之后网络的联合概率分布,p∞为马氏链末端的分布,用KL(p‖p′)表示p和p′之间的差异性,所以CDn就是pn衡量介于p0和p∞之间的位置。在运算中,不断地将pn赋值给p0,得到新的p0和pn。
在实验中令n=1,经过r次求斜率并用公式(4)修正θ,可以得到其值趋向于0的CDn,且实验结果的精度近似于马氏链方法。
2 实验与分析
相同网络结构下,增加训练样本容量可在一定程度上提高预测精度,但会增加试验次数。总样本容量的选择从30~300不等[12],其中训练样本和测试样本容量的经验比值为7:3。因此,本文确定总样本容量为68,其中训练样本数为48,测试样本数为20。样本采用3因素(工件转速vc、进给量fz、轴向切深ap)混合水平全组合模型实验,进给量安排了6个水平,工件转速安排4个水平,轴向切深安排了2个水平,具体实验训练样本参照文献[13]。
2.1实验设置
实验分两步进行,第一步,用48个训练样本值训练RBM,迭代次数为50,然后用训练好的RBM对48个训练样本进行分类,其中学习速率为0.01~0.02;第二,建立一个含有两层RBM的DBN网络,每个RBM含有100个神经元,输入48个训练样本,利用BP对48个训练样本进行微调,马氏链迭代次数为50,学习速率为0.01~0.02,训练要求精度为MSE=0.001,最后用训练好的DBN对20个测试组进行粗糙度值的预测。图2为改进的DBN模型训练误差曲线。
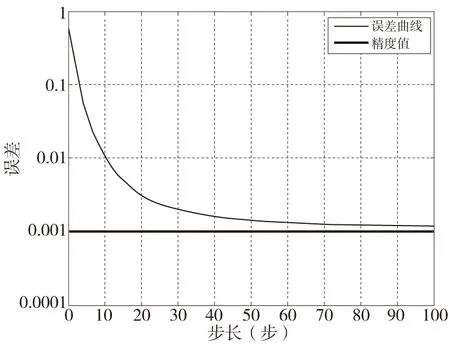
图2 改进深度神经网络模型训练误差曲线
2.2实验结果
表1所示为20个测试样本采用不同预测方法的平均相对误差。可以看出实测值与预测值,相对误差控制在10%以内,最大相对误差为6.8%,最小相对误差为5.9%,说明采用改进DBN模型预测的粗糙度值比较准确。

表1 RBM和DBN实验数据
表中黑色部分是改进网络的数据。
通过上边两个实验可以看出,改进方法的RBM较原始RBM在训练准确度上有所提高,并且通过使用两层RBM的叠加,DBN的训练精度也有较为明显的提升,证明了改进RBM的有效性。
3 结束语
本文针对算法的固定学习率引起的寻找最优值准确度不高的问题进行了改进,将改进策略应用于磨削表面粗糙度值的预测问题中,实验结果表明改进策略能够有效提高DBN的准确性,由于训练样本的选取均来自高精度形貌仪,通过本文提出的预测模型,只要获取磨削时的加工参数,即可完成对加工表面粗糙度值的预测,且预测误差在6%以下,应用该模型可有效的降低产品检测成本,具有较高的工程价值。
[1] 王洪详,李旦,董申.超精密车削表面粗糙度预测模型的建立[J].高技术通讯,2003(3):77-82.
[2] 苏宇,何宁,武凯,等.基于ANFIS的铝合金铣削加工表面粗糙度预测模型研究[J].中国机械工程,2005,16(6):475-479.
[3] 周斌,曹勇,王禹林,等.基于BP神经网络的大型螺纹旋风铣削表面粗糙度预测[J].组合机床与自动化加工技术,2015(7):5-10.
[4] 刘牧,杨茂奎.基于响应曲面法的表面粗糙度预测模型研究[J].机床与液压,2006(7):87-90.
[5] 陈杰来,孙俊兰.基于遗传神经网络的表面粗糙度预测模型研究[J].制造业自动化,2011,33(12):10-12.
[6] 刘晓志,陶华,李茂伟.钛合金TC18铣削表面粗糙度预测模型研究[J].组合机床与自动加工技术,2010(7):8-11.
[7] Hinton G E, Osindero S.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18:1527-1554.
[8] Yoshua Bengio,Pascal Lamblin,Dan Popovici,et al.Greedy Layer-Wise Training of Deep Networks[J].Advances in Neural Information Processing Systems 19 (NIPS 2006),MIT Press,2007,153-160.
[9] Y Bengio. Learning Deep Architectures for AI[Z].Foundations & Trends in Machine Learning,2009.
[10] Hinton GE. Products of experts[A].Proc. of the 9th Int’l Conf on Artificial Neural Networks(ICANN),Edinburgh,1999,1:1-6.
[11] Hinton GE. Training products of experts by minimizing contrastive divergence[J].Neural Computation, 2002,14(8):1771-1800.
[12] DAVIM J P,GAITONDE V N,KARMIK S R.Investigations into the effect of cutting conditions on surface roughness in turning of free machining steel by ANN models[J].Journal of Material Processing,2008,205(1-3):16-23.
[13] 陈廉清,郭建亮,杨勋,等.基于进化神经网络的磨削粗糙度预测模型[J].计算机集成制造系统,2013,19(11):2854-2863.
(编辑李秀敏)
The Application of Improved Deep Belief Network in Surface Roughness of Grinding
TIAN Yang
(Department of Research, Liaoning Engineering Vocational College,Tieling Liaoning 112000,China)
Deep Belief Network(DBN)is a kind of neural network classifier which is made of several Restricted Boltzmann Machines(RBMs)and a layer of BP. In order to improve the disadvantage in optimizing stage due to the fixed learning rate in RBM,this paper proposes a dynamic rule to it.A DBN that includes two RBMs and a BP and the rule of comparison and dispersion was adopted to conduct the rapid training of neural network.The improved network is applied to the prediction of surface roughness, and the accuracy of the model is improved by comparing with the prediction model and RBM model.
deep belief network;restricted boltzmann machine;surface roughness;prediction model
1001-2265(2016)07-0108-03DOI:10.13462/j.cnki.mmtamt.2016.07.031
2015-09-03;
2015-10-02
辽宁省教育厅科学研究一般项目(L2014589)
田杨(1980—),男,辽宁调兵山人,辽宁工程职业学院科研处副教授,博士,研究方向为数字化设计与制造, (E-mail)remlove@163.com。
TH164;TG65
A

