基于宏程序的椭圆孔插铣加工研究*
王庭俊
(扬州工业职业技术学院 机械工程学院,江苏 扬州 225127)
基于宏程序的椭圆孔插铣加工研究*
王庭俊
(扬州工业职业技术学院 机械工程学院,江苏 扬州225127)
插铣法是一种高效实用的切削加工方法,特别适用于难加工材料的深腔或通孔的粗加工和半精加工。在前期研究并发表的关于使用宏程序编程插铣加工矩形和圆形深腔的基础上,针对椭圆形孔的插铣孔中心的定位方法进行研究,并就部分论文将椭圆参数方程的离心角和椭圆图上标注的圆心角相混淆的情况进行了分析,确定出高效正确的椭圆孔插铣粗加工时插铣孔的定位计算方法,同时给出了插铣加工椭圆孔的加工实例和数控宏程序编制工艺。
椭圆孔;插铣加工;宏程序;离心角
0 引言
生产中插铣加工的使用日趋普遍,插铣法也称为Z轴铣削法,该法切削效率高、对机床精度要求不太高、切削的稳定性随着切削深度的增加而提高,特别适合于难加工材料的挖腔或通孔的加工。从作者已发表的圆形腔的插铣加工研究论文可知[1],该加工方法的关键是要确定各个插铣孔中心位置坐标,从而保证正确高效的完成插铣加工。
1 椭圆孔的插铣加工工艺
1.1图样分析
随着个性化需求的增加,椭圆形腔(孔)的加工越来越常见,图1所示为一椭圆孔的插铣粗加工示意图。
椭圆孔的加工是在已预置孔的厚板上进行轮廓的插铣粗加工或半精加工,即在椭圆轮廓内侧的插铣加工一周或两周,留下精加工余量进行周铣精加工,所以关键问题是依次相邻的插铣孔位置的确定。

图1 椭圆孔插铣粗加工示意图
1.2插铣动作分解
(1)将插铣刀快速定位到椭圆孔中心上方。
(2)插铣刀快速定位到椭圆孔X轴正向的最大值处(插铣刀中心和椭圆右侧象限点之间的距离为铣刀半径值r与精加工余量C之和)。
(3)插铣刀快速到达安全平面(R平面)。
(4)插铣加工第一个孔,到达Z平面后快速返回到R平面。
(5)由X轴正向逆时针定位插铣加工第二个孔,其周向位移步距为L。
(6)依此类推,直至一圈粗加工全部完成。
2 相关数学模型
2.1曲率圆与渐曲线
如图2作半径为名义铣刀半径R的圆与椭圆相切于点S(x,y),该圆的圆心为点C(x0,y0)。过点S作半径为M的曲率圆,该圆在S点处与椭圆不仅相切,且曲率和凹凸方向也一样,从而确定它们在S点处的函数值、一阶导数、二阶导数均相等[2]。
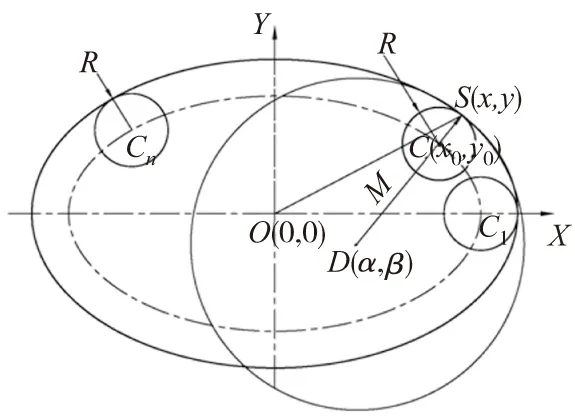
图2 椭圆相关几何量示意图
曲率中心坐标值为:
α=x-y′(1+y′2)/y″
β=y+(1+y′2)/y″
(1)
当S点延着椭圆移动时,得到的C1CCn曲线为该椭圆的一条渐曲线,也是插铣孔的中心线。
椭圆参数方程为:
x=a·cos(t)
y=b·sin(t)
(2)
由参数方程求导得:
(3)
则:
(4)
分别代入(1)式,得到曲率中心D点坐标值为:
α=(a2-b2)·cos3(t)/a
β=(b2-a2)·sin3(t)/b
(5)
图3所示三角形SDE,根据相似三角形,有:
(x-x0)/(x-α)=(y-y0)/(y-β)=R/M
(6)
则C点坐标值为:
x0=x-(x-α)·R/M
y0=y-(y-β)·R/M
(7)
其中曲率半径M值为:
(8)

图3 三角形SDE
2.2圆心角与离心角
椭圆的离心角即参数方程的参数t,而非椭圆上直接标注的圆心角θ,许多人将这两个角混淆[3],下面通过图4进行说明。
以原点O为圆心,分别以a、b为半径作两个圆。点A是大圆上任意一点,B是半径OA与小圆的交点,过点A作AN⊥X轴于点N,再过点B作BM⊥AN于点M。当半径OA绕点O旋转时,点M的轨迹就是椭圆,∠AON为椭圆的离心角t,∠MON为椭圆的圆心角θ。
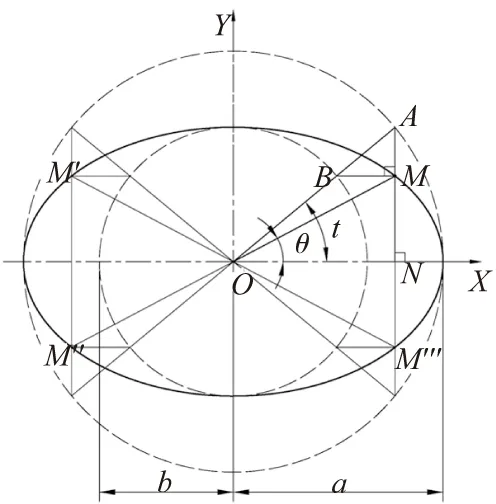
图4 椭圆的圆心角θ与离心角t的关系图
根据几何知识可得圆心角θ与离心角t的关系,以第一象限为例,根据图4,推导过程如下。
ON=AN/tan(t)=MN/tan(θ)
tan(t)/tan(θ)=AN/MN
而根据相似三角形得AN/MN=OA/OB=a/b
所以:
tan(t)/tan(θ)=a/b
即:
tan(t)=(a/b)·tan(θ)
亦:
t=arctan(a·tan(θ)/b)
(9)
同理在第二、第三象限有:
t=π+arctan(a·tan(θ)/b)
(10)
在第四象限有:
t=2π+arctan(a·tan(θ)/b)
(11)
3 插铣加工时有关几何量的计算
3.1插铣周向步距值L的确定
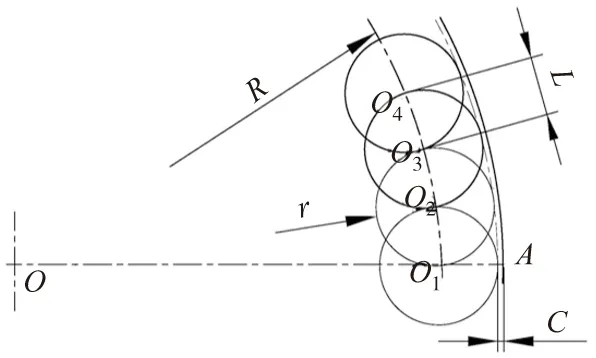
图5 粗插铣步距L的确定
为提高插铣加工效率,且不留下太多的残留加工面积,理想情况是取铣刀的半径值作为周向插铣步距,即L=r,其中r为铣刀的半径[4],如图5所示。
3.2周向步距L对应的圆心角增量△θ的确定
插铣加工时理想情况下相邻两个插孔中心所在位置如图6所示。

图6 步距L对应的圆心角增量△θ的确定
设插铣粗加工时刀具中心所在的圆半径为R,对应的弧长近似为周向步距L,则有
(12)
需要注意的是,因为椭圆的极距是变化的(即OO3≠OO4),即R是一个随着圆心角θ变化的变量,需逐次迭代求解。将第一个插铣孔C1定为X轴正向位置上,留有精加工余量(见图5),其中x01=A-r-C,y01=0;
则△θ1值为:
(13)
第二个插铣孔的中心角θ2=θ1+△θ1。在不少的论文中,把圆心角误当成离心角代入相关的参数方程进行计算,使S点和C点的位置计算值出现了很大的偏差。
由式(9)可得t2=arctan(a·tan(θ2)/b),由前面的公式代入t2计算出S2和D2及第二个孔的中心C2(x02、y02)的坐标值,依此类推,计算出C3、C4、…Cn,直到一整圈全部完成。
3.3编程实例
此例的椭圆长半轴为50mm,短半轴为40mm,插铣刀直径为10mm,精加工余量设为零。
(1)方案一:以圆心角简单替代离心角的模拟加工,效果图如图7所示。
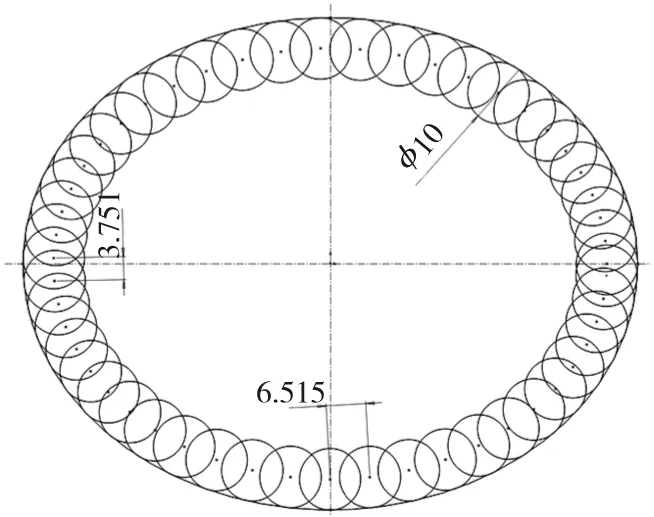
图7 用圆心角替代离心角的加工效果图
由该图可看出,插铣孔的最大间距为6.515mm,最小为3.751mm,与理想值5mm有着较大的差距,相对差值分别达到30.29%和-24.98%,疏密严重不均,大大降低了加工质量和效率。这主要是简单地以圆心角θ代替离心角t计算相关的几何量造成的。
(2)方案二:由圆心角计算出离心角,再计算出相关的几何量,加工效果如图8所示。
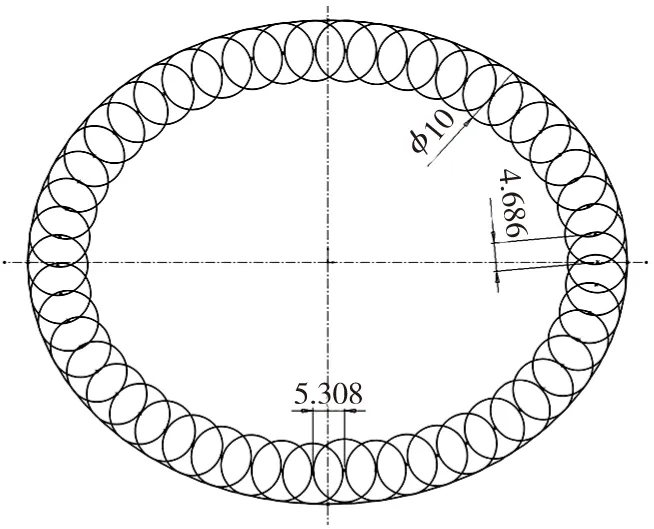
图8 以圆心角计算出离心角的加工效果图
由该图可看出,插铣孔距最大值降为5.308mm,最小值也增加为4.686mm,比较接近理想值5mm,相对差值分别降到了6.16%和-6.29%,疏密不均的情况极大的得以改善。
(3)方案对比:第二种方案疏密不均的现象明显好于第一种,为直观比较两种方案对应的插铣孔中心距变化的影响,按插铣孔序将两者的中心距变化情况作一对比如图9所示。可明显看出,第二种方案采用的由圆心角计算出离心角再得出相关位置点的方法,插孔中心距与理想值的偏差明显较小,约为第一种方案偏差值的五分之一,既改善了插铣粗加工时的不均匀度,又进一步减小了孔侧壁的残留面积的差异,有利于后续精加工质量的保证。

图9 两种离心角获得方式对应的插铣孔中心距变化对比图
两种方案均仍存在椭圆的上下象限点附近插铣孔距大,左右象限附近插铣孔距小,只是表现程度有所区别。究其原因,就是以插铣孔中心到椭圆腔中心的距离作为极角增量计算时的对应的半径,而在椭圆上距离椭圆中心距离较大处曲率半径反而较小,反之亦然,最终造成了插铣孔在圆周方向的疏密不均的现象。如需近一步改善疏密不均的现象,需要进一步对极角增量计算时的对应的圆半径R进行修正。
4 宏程序编制
4.1用户宏指令
设圆形深腔的宏程序号为O8000(自已设定)。
指令:G65P8000X_Y_Z_R_A_B_C_D_F_;
式中:
X,Y——椭圆孔的平面中心位置;
Z——插铣的深度Z坐标;
R——刀具快速趋近平面的Z坐标值(即R平面Z值);
A——椭圆的长半轴值;
B——椭圆的短半轴值;
C——椭圆孔的精加工余量;
D——插铣刀的直径;
F——插铣进给速度。
4.2用户宏程序
O8000插铣椭圆形孔宏程序名
#100=0;粗插铣圆心角t赋零初值
#109=#7/2+#3;插孔中心到S点距离
#108=#7/2;周向插铣步距L值
G00X#24Y#25;快速定位到椭圆中心
G52X#24Y#25;建立局部坐标系
G00Z#18;快速趋近R平面
WHILE[#100 LT360]DO1;插铣加工循环整圈判别
IF[#100LE90]THEN #110=ATAN[#1*TAN[#100]/#2];圆心角位于第一象限时,计算离心角t的值
IF[#100GT90]THEN #110=180+ATAN[#1*TAN[#100]/#2];圆心角位于第二、三象限时,计算离心角t的值
IF[#100GT270] THEN #110=360+ATAN[#1*TAN[#100]/#2];圆心角位于第四象限时,计算离心角t的值
#111=#1*COS[#110];插孔对应椭圆S点X值
#112=#2*SIN[#110];插孔对应椭圆S点Y值
#121=[#1*#1-#2*#2]*COS[#110] *COS[#110] *COS[#110]/#1;曲率圆中心横坐标值α
#122=[#2*#2-#1*#1]*SIN [#110]*SIN[#110]*SIN [#110]/#2;曲率圆中心纵坐标值β
#123=#111-#121;计算X-α值
#124=#111-#122;计算Y-β值
#125=SQRT[#123*#123+#124*#124];曲率半径M值
#101=#111-#123*#109/#125;插孔中心坐标X0值
#102=#112-#124*#109/#125;插孔中心坐标Y0值
G01 Z#26 F#9; 插铣加工到Z平面
G00 Z#18; 快速退回到R平面
#126=SQRT[#101*#101+#102*#102];插孔中心到椭圆中心距离
#128=180*#108/[3.142*#126];中心角增量值△θ
#100=#100+#128;中心角递增△θ值
END 01;插铣加工循环结束
G52 X0 Y0;取消局部坐标系
M99;返回主程序
5 结束语
(1)该例是针对插铣加工一圈就能完成粗加工的情况,如果粗加工的余量较大时,可采用循环嵌套的方法,分两圈插铣加工,具体见参考文献[1],在此不再详述。
(2)插铣刀的直径(D)不能大于椭圆的最小曲率半径值(B2/A)的两倍,否则会发生过切。
在分析非圆孔特点的基础上,建立数学模型并推导出相关参数表达式,利用数控系统的用户宏功能,开发具有通用性的非圆曲线轮廓加工宏程序[5],通过椭圆孔的插铣编程加工分析及仿真加工实例均可以看出,利用插铣法编制宏程序进行数控加工,不仅大大提高了切削加工效率,而且提高了手工数控编程的效率。
[1] 王庭俊,康峰华,赵东宏.基于宏程序的圆形深腔插铣加工[J].煤矿机械,2014,35(4):113-115.
[2] 王正方,徐桂根.椭圆孔的数控铣削及其误差分析[J].机械工人(冷加工),2000(10):33-34.
[3] 赵薇,薛明.斜椭圆类零件数控车削加工方法研究[J].组合机床与自动化加工技术,2014(1):146-148,152.
[4] 孙德茂.插铣法挖腔用户宏程序的编程[J].模具工程,2005(10):57-60.
[5] 苟建峰,彭美武,卢万强,等.基于渐变非圆曲线轮廓零件的参数编程研究[J].组合机床与自动化加工技术,2015(4):146-148.
(编辑赵蓉)
Research on Plunge Milling for Elliptic Hole Based on Macroprogram
WANG Ting-jun
(College of Mechanical Engineering, Yangzhou Polytechnic Institute, Yangzhou Jiangsu 225127, China)
The plunge milling is an effective and practical machining method, especially suitable for rough-machining and semi-finishing of hardworking material of deep cavity or through hole. The location method of center of plug hole milling of elliptic cavity hole was researched based on published in the early stage for used macro program programming to milled rectangular and circular cavity, the positioning calculation method of rough-machining of plunge milling for elliptic cavity hole was efficient and correct determined. At the same, the manufacture instance of plunge milling for elliptic cavity hole and the process planning of NC macro program were provided.
elliptic hole; plunge milling; macro program; eccentric angle
1001-2265(2016)07-0118-04DOI:10.13462/j.cnki.mmtamt.2016.07.034
2015-07-22
江苏省高校创新实践计划项目(201313754003Y)
王庭俊(1971—),男,江苏扬州人,扬州工业职业技术学院副教授,高级技师,硕士,研究方向为CAD/CAM、编程数控加工的教学和研究,(E-mail)wangtjzhuwb@163.com。
TH164;TG659
A

