初中概率问题求解的基本方法

刘佳



初中概率问题求解的基本方法

刘佳

概率问题的背景材料各种各样，与我们的生活越来越贴近，我们在解决概率问题时，需要根据题目的特点选择合适的方法.在初中阶段，我们主要接触到三类概率问题：第一种是利用频率估计概率；第二种是可以列举出所有实验结果的，我们用列举法；第三种是实验结果无限，不能使用列举法的，我们采用几何法解决.

一、估算法

例1历史上曾有人做过抛掷硬币的大量重复实验，结果如下表所示：

则估计抛掷一枚硬币正面朝上的概率为________.

人们在长期的实践中发现，在随机试验中，由于众多偶然因素的影响，每次测得的结果虽不尽相同，但大量的重复试验结果却能反映客观规律，这称为大数法则.因此我们可以通过多次试验，用一个事件发生的频率来估计这个事件发生的概率.

二、公式法

公式法主要解决一步试验发生的概率.

一般地，对于一个事件，所有可能出现的结果数共n种，其中满足某个条件的事件A出现的结果数是m种，那么事件A发生的概率为：

例2在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同.

（1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；

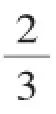
解：（1）∵共10个球，有2个黄球，

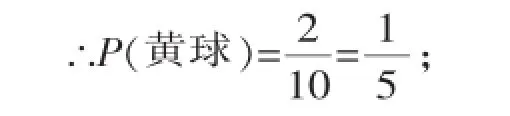
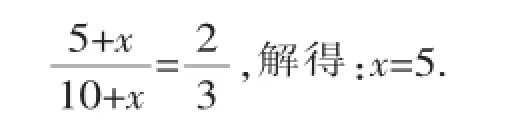
故后来放入袋中的红球有5个.

三、列表法和画树状图法

列表法和画树状图法主要用于两步试验发生的概率，它是将所有事件的可能结果画出来，再根据所有的结果求事件发生的概率.

例3为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采

（2）设有x个红球，根据题意得：用随机抽签方式.

请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率.

解：列表得：

所有等可能的情况有12种，其中第一、二位出场都是男选手的情况有6种，即：

例4在一个口袋中有4个完全相同的小球，把它们分别标上1、2、3、4.小明先随机摸出一个小球，小强再随机摸出一个小球.记小明摸出的球标号为x，小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则：当x＞y时小明获胜，否则小强获胜.

（1）若小明摸出的球不放回，求小明获胜的概率.

【分析】首先根据题意画出树状图，由树状图求得所有等可能的结果与小明获胜的情况，继而利用概率公式即可求得答案，注意此题属于不放回实验；

解：画树状图得：

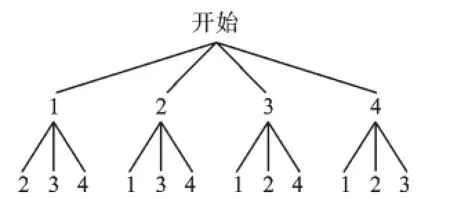
∵共有12种等可能的结果，小明获胜的有（2，1），（3，1），（3，2），（4，1），（4，2），（4，3）共6种情况，

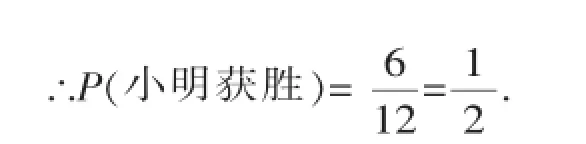
（2）若小明摸出的球放回后小强再随机摸球，问他们制定的游戏规则公平吗？请说明理由.

【分析】首先根据题意画出树状图，由树状图求得所有等可能的结果与小明、小强获胜的情况，继而利用概率公式求得其概率，比较概率，则可得到他们制定的游戏规则是否公平，注意此题属于放回实验.

解：画树状图得：

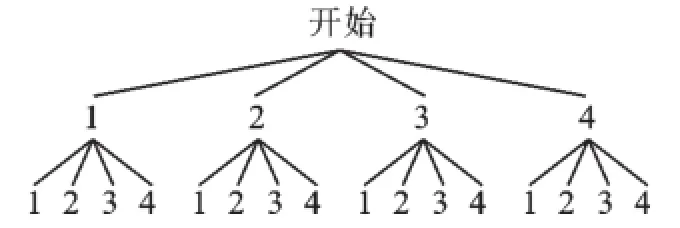
∵共有16种等可能的结果，小明获胜的有（2，1），（3，1），（3，2），（4，1），（4，2），（4，3）共6种情况，

∵P（小明获胜）≠P（小强获胜），

∴他们制定的游戏规则不公平.

四、几何法

有一类随机试验的结果是无限的，其概率的计算方法：设试验结果落在某个区域S中的每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那

例5有一块边长为30 cm的正方形飞镖游戏板ABCD，假设飞镖投在游戏板上的每一点的机会均等.求下列事件发生的概率：

（1）在飞镖游戏板上画有半径为5 cm的一个圆（如图1），求飞镖落在圆内的概率；

（2）飞镖在游戏板上的落点记为点O，求△OAB为钝角三角形的概率.

图1　

备用图

【分析】（1）分别计算半径为5cm的圆的面积和边长为30 cm的正方形ABCD的面积，即可求出飞镖落在圆内的概率；

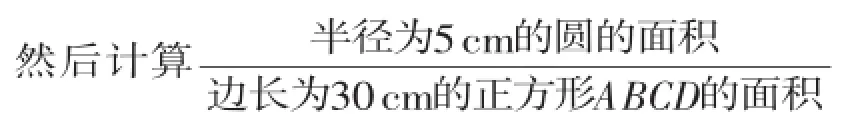
（2）根据题意及结合图形可得：当点O落在以AB为直径的半圆内时，△OAB为钝角三角形.计算以AB为直径的半圆的面积，用半圆的面积除以正方形的面积即可求△OAB为钝角三角形的概率.

解：（1）圆的面积为π·52=25π（cm2），

正方形的面积为302=900（cm2），

（2）如图2可得：当点O落在以AB为直径的半圆内时，△OAB为钝角三角形.

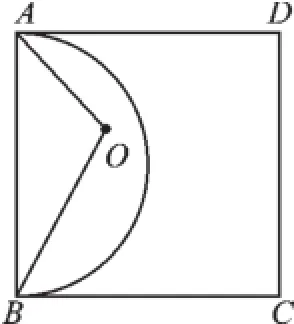
图2　

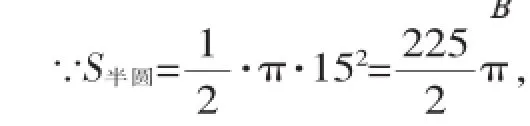
如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型.几何概型的具体内容到高中才学习，但中考中常作为材料阅读题，考查同学们对材料的理解和运用能力，这一类几何概率问题也是可以解决的.因此，几何法也可作为初中求解概率问题的一种方法.

（作者单位：江苏省常州外国语学校）