模型降阶算法在互连线系统仿真中的应用

马方超

(同济大学 电子与信息工程学院， 上海 201804)



模型降阶算法在互连线系统仿真中的应用

马方超

(同济大学 电子与信息工程学院， 上海 201804)

在进行集成电路系统的仿真时，如何加快含有互连线寄生效应所产生的延时信息的计算变得尤为重要。采用模型降阶的方式对具有互连线寄生效应的电路系统系数矩阵进行降阶，以达到加快含有互连线延时信息的互连电路仿真速度的目的。通过泰勒级数展开的高阶逼近技术，将传递函数中的e-sτ项进行多项式展开逼近，而后采用高阶Arnoldi算法进行降阶，所以降阶算法继承了传统矩匹配算法的保持无源性和结构性的优点，又能保证一定的精确度。算法最初的目标降阶数采用Hankel奇异值决定，减少了降阶的迭代次数，大大缩减了计算时间。

互连线寄生效应；泰勒级数展开；高阶逼近；矩匹配

0　引言

集成电路是整个信息产业发展的基础,而电子设计自动化(EDA)则是支持集成电路高速发展的支柱。在早期的小规模电路中，互连线的尺寸远小于信号波长，相对于门上时延，互连线的时延很小可以忽略不计。但随着工艺的不断进步，互连线尺寸逐渐缩小，电路工作频率进入GHz水平，使得互连线寄生效应也越来越明显，互连线的时延与门上时延更加接近，因此互连线的时延已经不可忽略。

常见的互连线寄生效应主要由趋肤效应、衬底效应和串扰等组成。为了精确描述互连线寄生效应，一般采用寄生参数提取的方式，即获取互连线的等效模型及其等效参数。本文电路模型针对互连线寄生效应中的趋肤效应采用部分元等效电路(PEEC)的方法对趋肤效应进行分析，完成互连线寄生电阻与寄生电感的参数提取。模型还会考虑互连线与衬底间的电容耦合效应，互连线间的串扰和衬底损耗等因素，使得互连线等效电路模型更加精确。对于大规模集成电路中的互连线而言，寄生参数提取之后的电路仿真需要求解的电路节点数会达到千万以上的量级，如果使用传统的Spice进行仿真则时间过长。因此在计算含时间延迟的电路模型时引入模型降阶的思想，以达到简化电路模型从而大大加快计算速度的目的。

模型降阶方法是分析互连线电路的有效方法之一[1]。模型降阶中比较成熟的一类算法是基于矩匹配的算法，例如传统的SPRIM算法[2]，其通过块Arnoldi降阶的方式在保证了系统无源性的前提下更能完全地保证电路系统的结构性，使得模型降阶算法在实际中加快电路仿真速度有了现实意义。针对互连线寄生效应所带来的互连线延时问题，本文将传统的矩匹配降阶算法改进为更加适合计算处理该种含有互连线时延信息的电路系统的仿真算法。

1　互连线电路模型

因为要满足制造工艺原则，芯片内部的互连线实质上是一条条具有不同长度、厚度和宽度的导线[3]。在现实研究仿真中，由于工作在高频中的互连线的寄生效应(如趋肤效应、串扰等)越来越显著，如何快速地建立一种高速精确的互连线模型成为集成电路仿真中的首要工作。

1.1PEEC模型

对于一个双互连线模型[4],在考虑到互连线的趋肤效应与衬底损耗两种情况下，本文给出与实际情况非常接近的PEEC模型。PEEC模型是基于PEEC法的等效电路模型，PEEC法通过对互连线单元切割的方式，能够精确计算在趋肤效应影响下的互连线自身的寄生电阻Rs与寄生电感Ls。将衬底效应与衬底损耗、线间串扰等因素一起考虑到等效电路中，可以得到等效模型如图1所示。其中Csub与Rsub为衬底电性损耗模拟，Cox1与Cox2为互联线与衬底形成的电容等效，Cm为线间串扰。

图1　双互连线PEEC等效模型

1.2PEEC模型延时计算

本文采用Elmore方法对互连线延时τ进行计算，因为采用PEEC提取的电路模型实质上是RLC树状模型(不考虑衬底损耗对延时造成的影响)。此时：

2　降阶算法推导

通过泰勒级数展开的方式，将传递函数中含有的e-sτi项进行展开逼近，而后采用高阶Arnoldi算法实现降阶。因此降阶后的矩阵拥有了SPRIM降阶算法的保持无源性和结构性的优点，又确保了很好的精确度。又因为算法最开始通过对hankel矩阵奇异值进行分析求取初始最优降阶数，减少了降阶算法的迭代次数，大大加快了计算速度。

2.1传递函数转化

对于一个含有k个τj时延的n维p口电路网络，其传递函数为[5]：

(1)

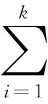
2.2零阶逼近

在s域中将e-sτi在s=0处泰勒级数展开：

当取零阶逼近时，

此时有:

此时传递函数在s域中表示为[6]：

H(s)=C(sET(s)-AT(s))-1B

(2)

对于传递函数H(u)，其可控Gramian矩阵为：

R=[B,ATB,AT2B,...,ATr-1B,...]

可观Gramian矩阵为：

L=[CT,ATTCT,(ATT)2CT,...,(ATT)r-1CT,...]T

2.3高阶逼近

对e-sτi进行r阶逼近时有：

此时可得：

转化后的传递函数为：

H(s)=C(mr+1sr+1+mrsr+...+m0)-1B

(3)

其中:

矩阵降阶过程如下：

令G=m0-1B,Lj=m0-1mj，K0=G

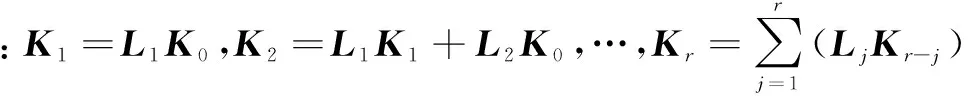
令：K=[K0,K1,K2,…,Kr],可以得到其r阶的Krylov 子空间为[6]:

Kq(L1,…,Lr,G)≡colsp(K)

(4)

由给定的Krylov子空间(4)和最优降阶数r求得降阶矩阵Xk：

colsp(Xk)=Kq(L1,...,Lr,G)

通过降阶矩阵Xk对传递函数中的系数矩阵进行降阶：

(5)

降阶之后传递函数变为：

(6)

3　实验仿真验证

本文实验采用两条并行的单位长度的金属线，等效为一个2×2的PEEC模型，如图2所示，每条互连线由20段PEEC单元等效模型组成，其中CL是负载电容。

使用hankel奇异值的方法求得初始最优降阶数为14，经迭代后求得最终最优目标降阶数为16。使用本文提出的降阶算法以及传统降阶算法与降阶前传递函数的频域响应对比，如图3所示。不同方法对应的电路仿真的CPU运行时间对比如表1。

由图3可以看出在频域上，本文提出的降阶算法降阶前后频率响应几乎一致,图中表现为三角形曲线与五角星曲线几乎完全重合。改进后的降阶算法与传统的降阶算法相比，在处理含有时延信息的计算上更为精确。由表1可以看出，采用本文所提出的算法，在电路仿真速度上提高了近200倍。

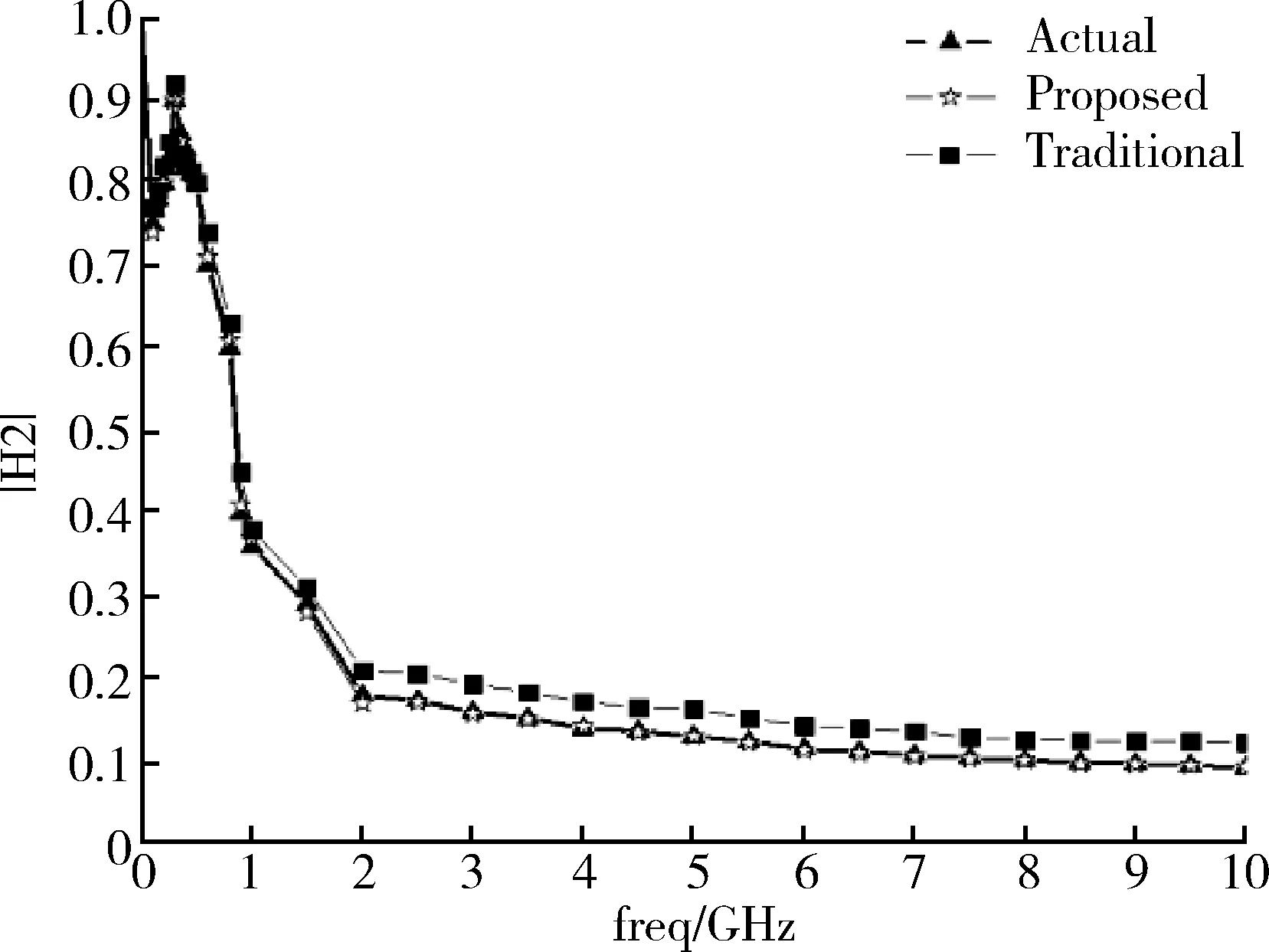
图3　降阶前后系统的频率响应

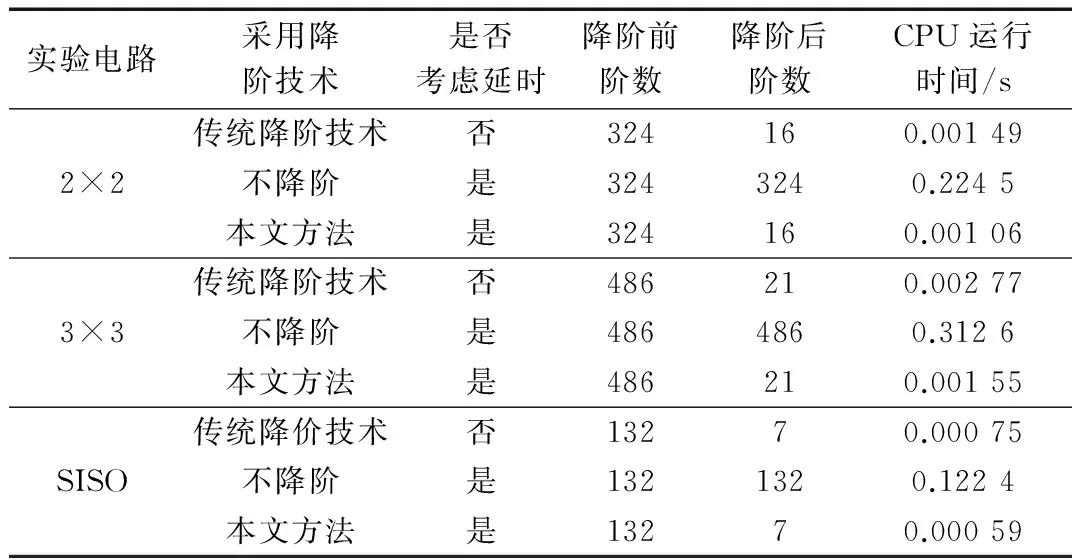
实验电路采用降阶技术是否考虑延时降阶前阶数降阶后阶数CPU运行时间/s2×2传统降阶技术否324160.00149不降阶是3243240.2245本文方法是324160.001063×3传统降阶技术否486210.00277不降阶是4864860.3126本文方法是486210.00155SISO传统降价技术否13270.00075不降阶是1321320.1224本文方法是13270.00059

[1] 蒋耀林.模型降阶方法[M].北京：科学出版社， 2010.

[2] FREUND R W. SPRIM: structure-preserving reduced-order interconnect macromodeling[C]. In IEEE/ACM International Conference on Computer Aided Design, 2004: 80-87.

[3] 扬帆.集成电路分析中的模型降阶方法研究[D].上海：复旦大学，2008.

图2　2×2互连线PEEC等效模型

[4] 尤焕成.SPICE兼容的RF传输线建模[D].成都：电子科技大学，2007.

[5] MICHIELS W, JARLEBRING E, MEERBERGEN K. Krylov-based model order reduction of time-delay systems[J]. SIAM J. Matrix Anal.Appl.,2011：32(4)：1399-1421.

[6] RASEKH E, DOUNAVIS A. Multiorder arnoldi approach for model order reduction of PEEC models with retardation[J]. IEEE Transactions on Components Packaging and Manufacturing Technology, 2012,2(10):1629-1636.

Application of model reduction algorithm for the simulation of interconnect system

Ma Fangchao

(Electronic and Information Engineering College , Tongji University, Shanghai 201804, China)

During integrated circuit system’s simulation, it becomes particularly important about how to speed up the calculation of interconnection’s delay. For accelerating simulation’s speed of interconnect system with delay information, model reduction method is adopted to achieve reduction of interconnected circuit system’s coefficient matrix. With high-order approximation technique of Taylor series expansion, the transfer function’s e-sτitem is converted a polynomials, then uses the high-order Arnoldi algorithm to finish reduction. So reduction method proposed inherits the advantages of passive and structural of tradition moment matching algorithm,and has a high precision. Since the algorithm uses the initial optimal target number decided from singular value of Hankel matrix, so the calculation time is decreased by reducing iteration’s time.

interconnect parasitic effect ;Taylor series; high-order approximation; moment matching

TN40

A

10.19358/j.issn.1674- 7720.2016.15.025

2016-03-06)

马方超(1990-)，男，硕士研究生，主要研究方向：大规模集成电路自动化仿真。

引用格式：马方超. 模型降阶算法在互连线系统仿真中的应用[J].微型机与应用，2016,35(15)：86-88,95.