一种新型原边反馈反激变换器数字采样算法设计*
顾新艳,程松林,王 冲
(1.南京工程学院汽车与轨道交通学院,南京211167;2.东南大学国家专用集成电路系统工程技术研究中心,南京210096)
一种新型原边反馈反激变换器数字采样算法设计*
顾新艳1*,程松林2,王冲2
(1.南京工程学院汽车与轨道交通学院,南京211167;2.东南大学国家专用集成电路系统工程技术研究中心,南京210096)
为了实现原边反馈反激变换器的高精度采样,提出了一种新型的数字采样控制算法。该算法根据变压器辅助绕组两端电压信息调整误差信号大小,并输入到内部控制环路实现对输出电压的稳定调节,相比于传统的采样电路,该方法省去了ADC或DAC电路,节省了控制电路的面积和功率的开销。本算法通过MATLAB仿真,且在一款5 V/1 A的AC-DC电源样机上验证了其有效性,其中恒压精度达到0.5%,表明该算法有很好的采样实时性、精确性和实用性。
反激变换器;数字采样;误差信号;原边反馈调节
反激式电源由于电路结构简单、适合多路输出、输入对输出电压影响小等优点[1-2],广泛应用于小功率电源适配器中。反激式电源变换器根据其反馈方式不同可分为原边反馈PSR(Primary Side Regulation)和副边反馈。副边反馈在变压器原边和副边之间引入一个光耦,通过光耦采样输出信号,其能够提供精确的恒流和恒压控制[3],但电路组件数目较多、成本较高、可靠性较低,更主要的是光耦在高温下线性度不好,误差较大。而PSR则通过在变压器中引入一个辅助绕组,进行输出信号的采样[4]。相比于副边反馈,原边反馈省去了采样光耦、减少了电路组件数目、降低了电路复杂程度,正逐渐成为未来反激变换器的发展趋势,同时也是现在国际上的研究热点。
采样技术在PSR反激电源的控制中起到重要作用,现在大致有两种方案:一是直接利用模数转换器ADC(Analog to Digital Converter)进行采样[5-6],二是利用带有数模转换器DAC(Digital to Analog Converter)的采样算法实现[7-8]。但是这两种方案都会带来较大的电路开销,增加控制电路的复杂度和成本。为了降低采样电路成本,本文提出了一种新型的数字采样算法,该方法采用固定基准电压与辅助绕组电压比较的结果经过数字运算得到输出电压的大小,在省去ADC 和DAC电路的同时,保持了采样的实时性与准确性。
1 原边反馈反激变换器原理
PSR反激变换器的电路主拓扑[9]如图1所示,输入交流电源经过整流桥到达滤波电容C1,在C1作用下得到一个低频波动的直流电压Vg(t)。电阻R3、电容C3及二极管D4组成RCD钳位电路,防止开关管Q1的漏端电压过高,因为在Q1的关断瞬间,其漏端电压会迅速上升,没有该钳位电路,Q1很可能会由于漏端电压过高而损坏[10-11]。变压器T1是该电路的核心之一,它有3个绕组,分别为原边绕组、辅助绕组和副边绕组,其中副边绕组和辅助绕组同名端方向相同,并且和原边绕组同名端方向相反。原边绕组在Q1导通期间存储能量,Q1断开瞬间能量耦合到副边绕组,副边绕组通过续流二极管D3和储能电容C2把能量供给负载RL。辅助绕组两端接分压电阻R1和R2,两个分压电阻可取较大阻值以保证低损耗。原边反馈反激变换器的采样模块根据分压电阻R2两端电压Vsense得到误差信号e(n),该误差信号输入到控制模块,控制模块根据e(n)和电流采样电阻Rsense两端电压Vp通过环路控制算法进行调节,从而输出合适的占空比duty使系统稳定输出。
项目来源:国家自然科学基金项目(51405221)
收稿日期:2015-07-28修改日期:2015-08-30
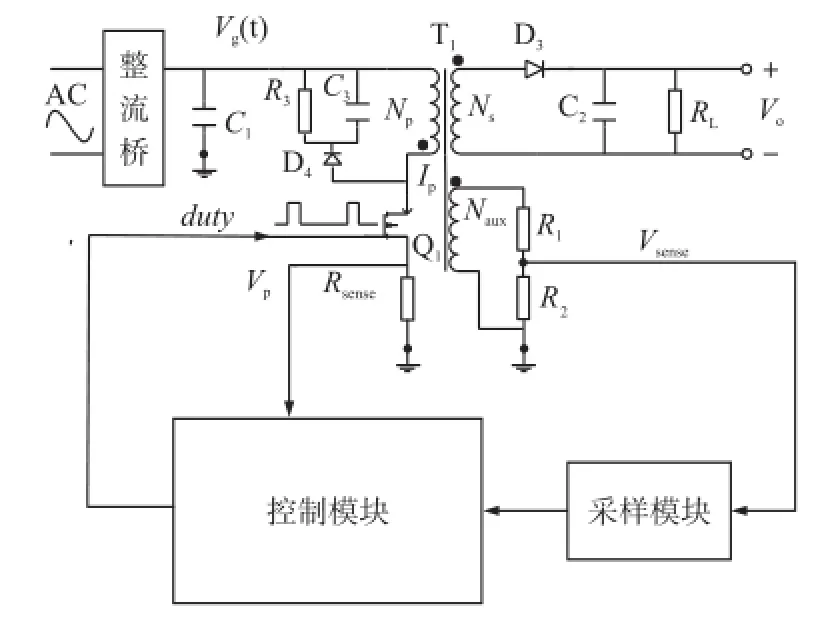
图1 原边反馈反激变换器系统架构图
2 采样算法理论分析
图2中展示了PSR反激电源中原边绕组Np电流Ip、副边绕组Ns电流Is、采样信号Vsense和占空比信号duty的波形,下面重点分析开关断开后电压Vsense的变化情况。
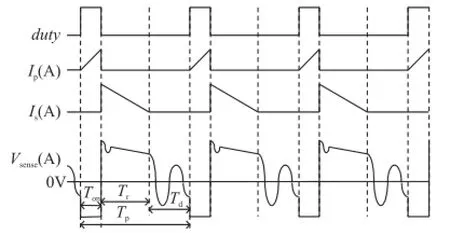
图2 原边反馈反激变换器关键波形
当开关关断后,原边绕组存储的能量会耦合到副边绕组,续流二极管D3有电流流过,并且线性减小,直到减小到0,这段时间称为Tr,在此期间,Is如式(1)所示:
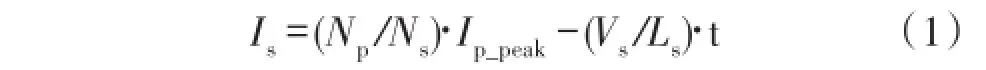
式(1)中,Np为原边绕组匝数,Ns为副边绕组匝数,Ip_peak为Ip峰值,Ls为副边绕组电感,Vs为副边绕组两端电压,Is降为0时刻t的大小如式(2)所示:
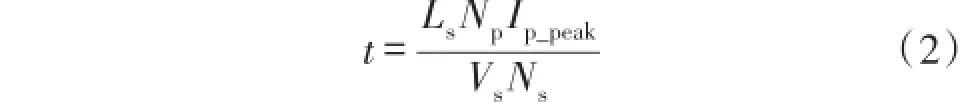
式(2)中t代表图中时间Tr的大小,副边绕组两端电压Vs满足式(3):
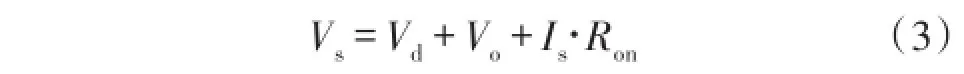
式(3)中Vd代表D3导通压降,Ron为其导通电阻。根据式(1)和式(2)可得到式(4):
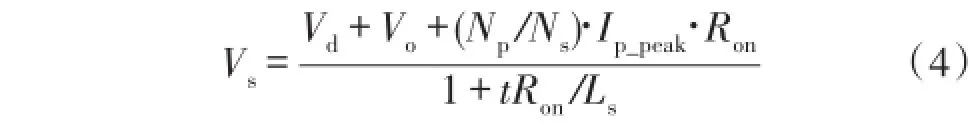
式(4)表示了Vs与Vo和t的关系,根据变压器的特性,副边绕组两端电压和辅助绕组两端电压存在着固定的比例关系,所以当Vs与输出电压Vo相等时,采样电压Vsense与输出电压也有着固定的比例关系,此时t可以用式(5)表示。
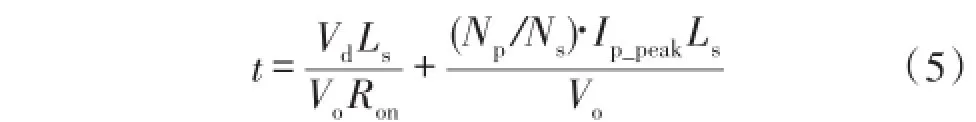
通过比较式(2)和式(5)时间的大小关系可知,式(5)表示的t略大于Tr,说明在Is为0的时刻副边绕组两端电压大于输出电压,所以在续流二极管降为0时刻采样并不是最准确的,如图3所示。
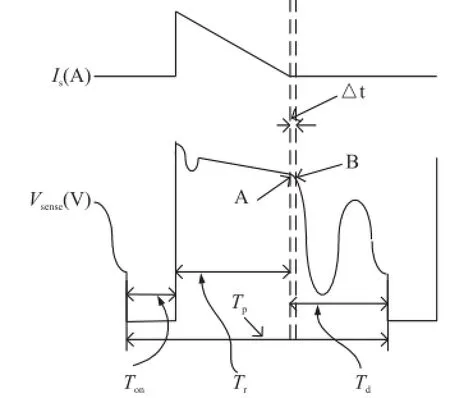
图3 数字原边采样方案波形关系图
当电流Is降为0时,采样电压Vsense开始从峰值A处正弦衰减振荡,并且衰减振荡的周期固定。此时Vsense的值并不和Vo成固定比例关系,经过Δt时间后B处Vsense和Vo呈固定比例关系,并且满足式(6):
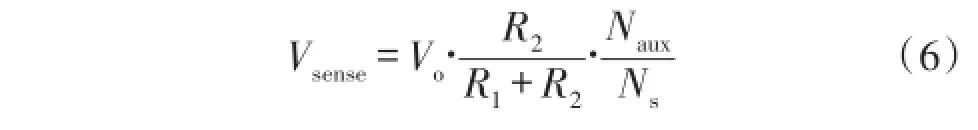
3 采样算法实现
由上节分析可得,在图3中的B处进行采样更为合理,这里给出了一种新型的数字采样方案,与现有的数字采样方案相比,省去了DAC和ADC,节省了芯片的面积和功耗,并且更为精确,采样模块的架构如图4所示。
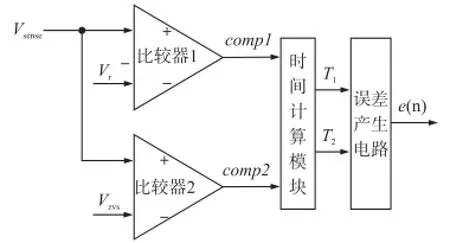
图4 数字采样模块算法原理架构图
图4中Vzvs是0电位电压,电压Vr是一个固定电位电压,其大小可用式(7)表示:
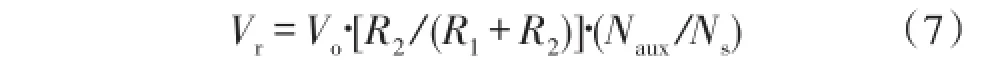
式(7)中Vo代表预期输出电压,R1和R2代表采样分压电阻,根据上面分析可知当Vsense和Vr相交于图3 中B点时代表输出电压稳定在预期值,当Vsense和Vr相交于图3中B点下面时代表输出电压偏大,当Vsense和Vr相交于图3中B点上面或没有交点时,代表输出电压偏小,根据输出电压是否偏离稳定值,Vsense、Vr和Vzvs不同情况下关系如图5所示。
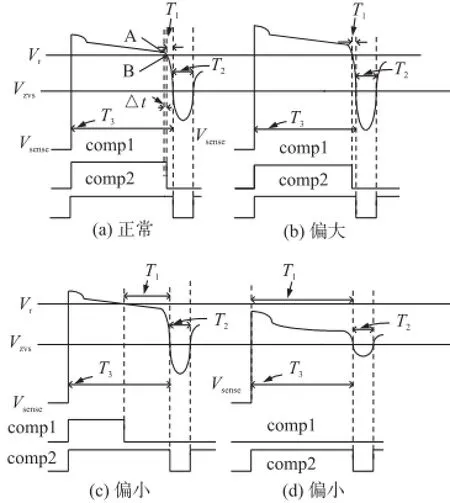
图5 采样方案中不同情况的工作波形图
如图5(a)所示,Vsense和Vr相较于B点,此时输出电压稳定,比较器1和比较器2的输出波形输入到时间产生模块,时间产生模块根据内部计数器得到时间信息T1和T2,在图5(a)中T1和T2满足T2/2-T1=Δt,此时误差产生电路检测到该状态,则输出一个大小为0的数字误差信号e(n),表示没有误差;在图5(b)中T1和T2满足T2/2-T1>Δt,此时误差产生电路检测到这个状态,将输出一个负的数字误差信号e(n),其具体大小根据T2/2和T1差值来设定,T2/2和T1差值越大,表明输出电压偏离的越大,产生的数字误差信号e(n)的绝对值则越大;在图5(c)中T1和T2满足T2/2-T1<Δt,此时误差产生电路检测到这个状态,将输出一个正的数字误差信号e(n),其具体大小根据T2/2和T1差值设定,T2/2和T1差值越大,表明输出电压偏离越大,产生的数字误差信号e(n)的绝对值就越大;在图5(d)中Vr和Vsense没有交点,此时表明输出电压还很小,误差产生电路得到一个最大的数字误差信号e(n)。采样模块除了可以得到误差信号,还可以得到Tr时间的大小,具体可表示为Tr=T3-T2/2,其中T3表示为开关关断后comp2的第1个高电平维持时间宽度。
上面阐述了采样算法的基本原理,但是仍然有一个问题没有解决,那就是如何确定Δt,根据正弦波形的特性,在图3中A点附近的波形斜率最小,在B点附近波形斜率也很小,但是和A处比已经偏大了,由于采样算法的时间信息是通过计数器计数得到的,所以采样波形斜率越小采样的精度就越高,为了提高采样精度可以设定Δt为0。但是设定Δt为0,根据前面理论分析可知输出电压不能稳定在预期值,而且比预期值小,为了解决这个问题,可以引入一个修正因子a,具体大小可以用式(8)表示:
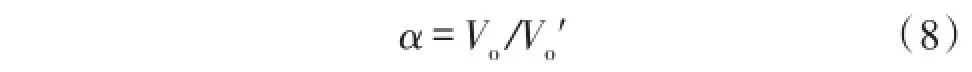
式(8)中Vo表示预期输出电压值,Vo'表示实际输出电压值,根据具体的仿真和测试得到修正因子a,然后通过改变分压电阻比或变压器匝数比来实现对输出电压的调节。
4 采样算法仿真验证
4.1仿真平台
为了验证所提算法,这里搭建了一个基于MATLAB的5 V/1 A PSR反激电源仿真平台,表1给出了反激变换器的主要参数。
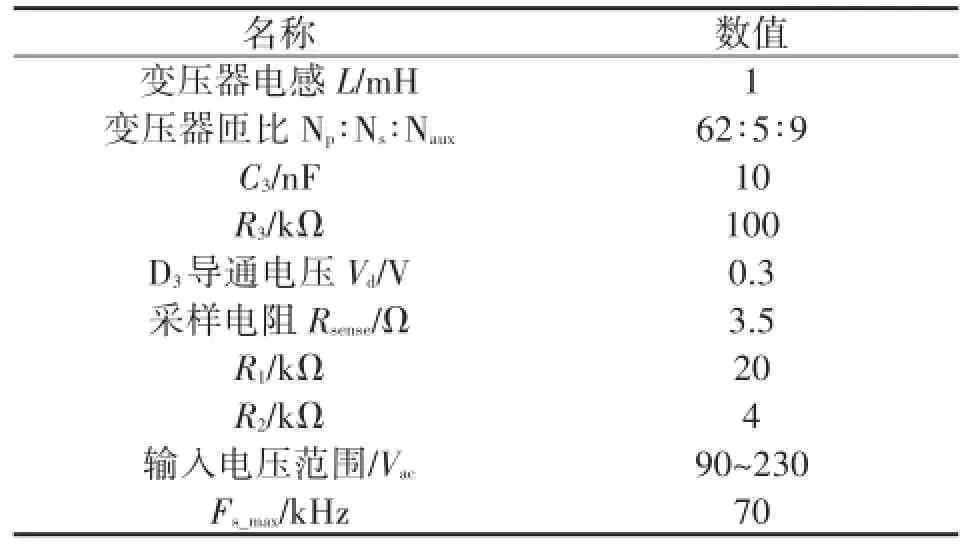
表1 反激变换器参数
图6是PSR反激电源的仿真平台,图6(a)是反激电源的控制环路拓扑,图6(b)是图6(a)子模块反激系统的电路拓扑,图6(c)是图6(a)子模块采样模块的比较器电路。
为了尽可能获得较高的采样精度,整个数字电路工作时钟频率为40 MHz,Δt设定为0。固定电压Vr的大小为1.458V左右。表2给出了T2/2-T1同e(n)关系。

图6 PSR反激电源的仿真平台
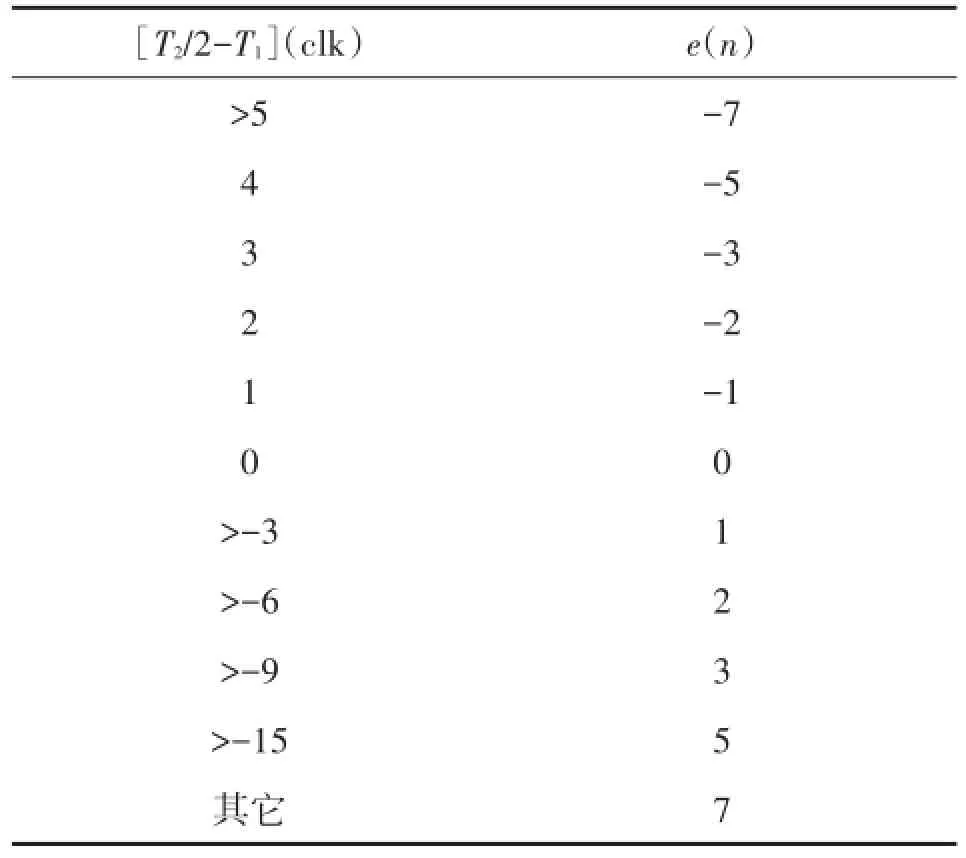
表2 T2/2-T1同e(n)关系
4.2仿真结果分析
根据前面分析,将分别仿真修正因子加入前后,输出电压Vo稳态变化情况,仿真的输入电压为交流220 V,仿真结果如图7和图8所示。
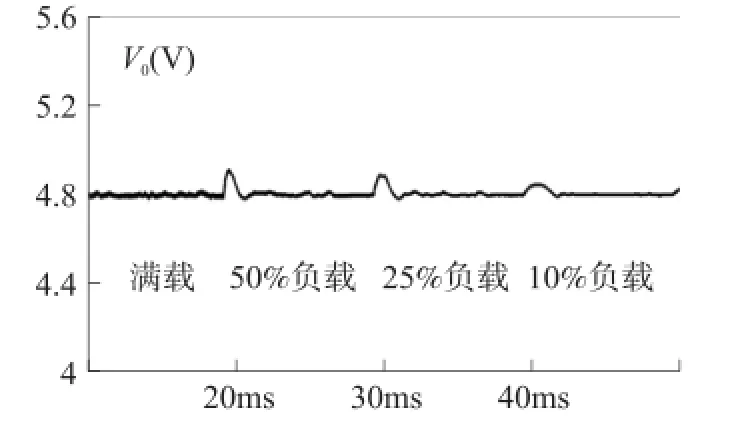
图7 未加修正因子时输出电压波形
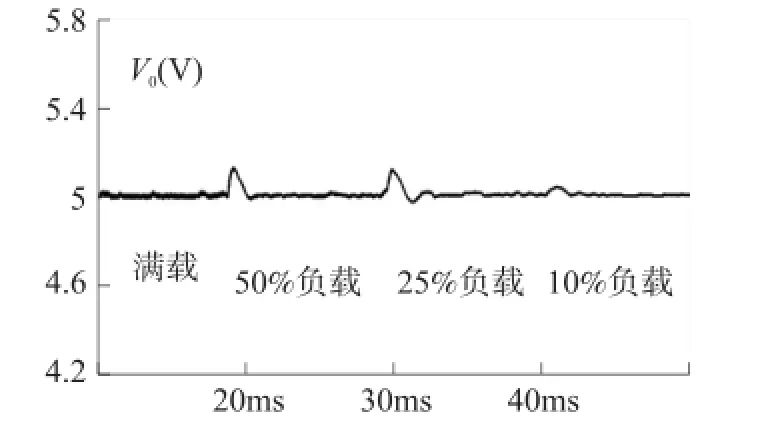
图8 加入修正因子时输出电压波形
图7和图8分别展示了未加入修正因子和加入修正因子时输出电压波形,可以发现整体输出电压稳压效果较好,在全负载范围内输出电压精度控制在了±0.5%之内。此外,同理论分析一致,在未加入修正因子时输出电压的稳定值小于5 V,加入修正因子之后输出电压的稳定值控制在了5 V,仿真时修正因子的加入是通过改变采样电阻分压比来实现的。
为了验证所提数字采样算法的动态跟随特性,对交流220 V输入电压下,满载和10%负载之间切换时Vo动态特性进行了仿真分析,如图9所示。
在图9中,仿真了负载切换时输出电压响应波形和电流采样电阻两端的电压Vp波形。满载切换到10%负载时,响应时间为4.5 ms;10%负载切换到满载时,响应时间为0.94 ms。同参考文献[11]相比,本文所提采样算法在省去DAC的前提下同样获得了比较好的动态跟随效果。
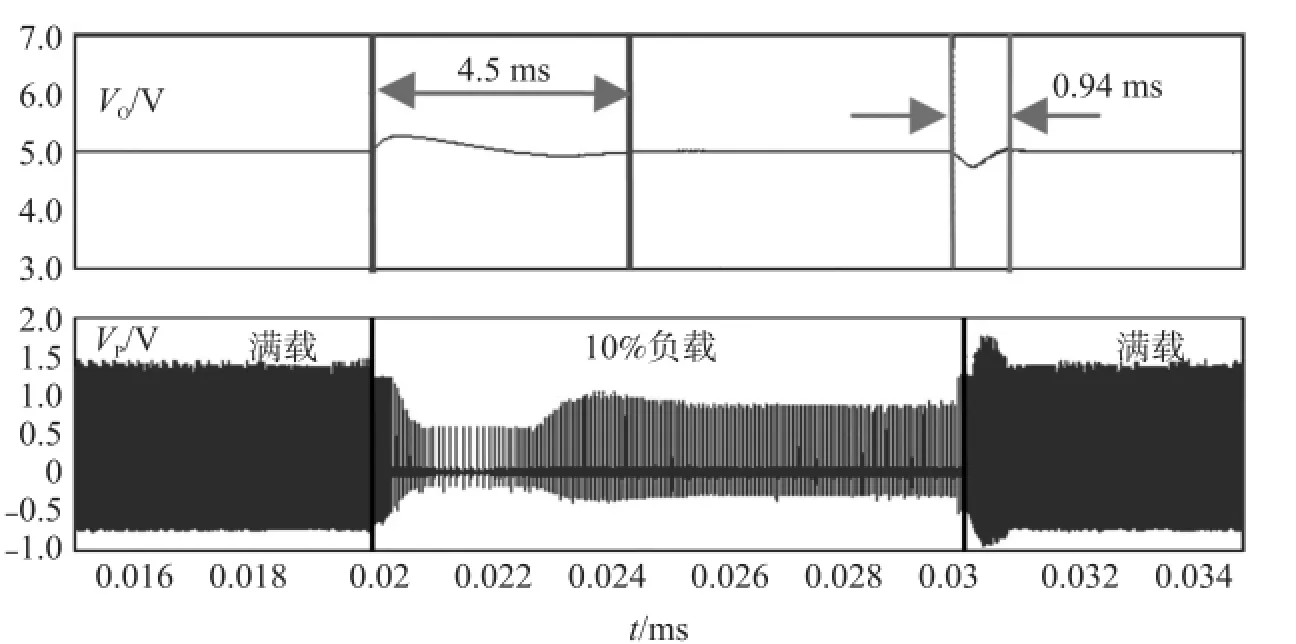
图9 满载和10%负载切换时输出电压响应波形
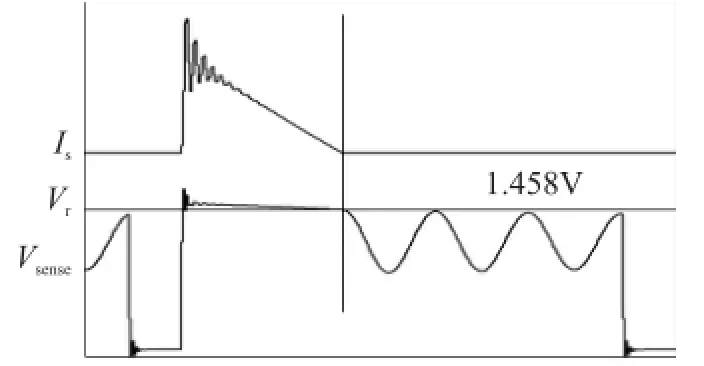
图10 采样波形图
图10展示了电压稳在5 V时,Vsense、Vr和副边电流Is波形,可以发现Vr和Vsense的交点处于副边电流降为0后的一点。与参考文献[6-7]相比,本算法的一个优点就是省去了DAC电路,在0.18 μm工艺下,一个DAC电路大约要占到整个芯片面积的1/6左右,所以在芯片设计时,芯片的面积和功耗将得到有效减少。
5 结束语
本文针对原边反馈反激变换器现有采样算法的缺陷,设计了一种新型的数字采样算法,省去了传统采样算法所应用的ADC或DAC电路,减小了电路开销和损耗,通过加入修正因子,在保持实时性的同时做到了更为精确的采样,最后通过仿真验证了所提算法的有效性,仿真结果和理论分析一致,所提算法具有一定的理论和工程应用价值。
[1] 普利斯曼,比得斯,莫瑞.开关电源设计[M].第2版.北京:电子工业出版社,2005:71-72.
[2] 鲍小亮.多调制模式反激式变换器的研究与设计[D].电子科技大学,2009.
[3] 张伟东,何杞鑫.一种适用于准谐振AC/DC控制芯片的波谷检测电路[J].电子器件,2008,31(6):1786-1789.
[4] Li Y C,Chen C L.A Novel Primary-Side Regulation Scheme for Single-Stage High-Power-Factor AC-DC LED Driving Circuit[J]. IEEE Transactions on Industrial Electronics,2013,60(11):4978-4986.
[5] Chang C W,Lin Y T,Tzou Y Y.Digital Primary-Side Sensing Control for Flyback Converters[C]//International Conference on Power Electronics and Drive Systems,IEEE,2009:689-694.
[6] Kang S H,Maksimovic D.Simplified Sensing and A/D Conversion for Digitally Controlled Flyback DC-DC Converters with On-Line Efficiency Optimization[C]//Applied Power Electronics Conference and Exposition(APEC),2012 Twenty-Seventh Annual IEEE,IEEE,2012:1075-1082.
[7] Lin A M L,Eason M D,Muegge M R.Power Converter Controller Controlled by Variable Reference Voltage Generated by Dual Output Digital to Analog Converter[P].U.S.Patent 7,589,983. 2009-09-15.
[8] 邱建平,林玲,何乐年.反激式开关电源控制芯片中的高精度原边反馈技术[J].电路与系统学报,2013,18(1):403-407.
[9] Hwang J T,Jung M S,Kim D H,et al.Off-the-line Primary Side Regulation LED Lamp Driver with Single-Stage PFC and TRIAC Dimming Using LED Forward Voltage and Duty Variation Tracking Control[J].IEEE Journal of Solid-State Circuits,2012,47 (12):3081-3094.
[10]Meng P,Wu X,Yang J,et al.Analysis and Design Considerations for EMI and Losses of RCD Snubber in Flybackconverter[C]//Applied Power Electronics Conference and Exposition(APEC),2010 Twenty-Fifth Annual IEEE,IEEE,2010:642-647.
[11]王冲.基于损耗模型的原边反馈反激电源数字多模式设计[D].南京:东南大学,2014.
[12]Qiu J,He L,Wang Y.A Multimode Digital Controller IC for Flyback Converter with High Accuracy Primary-Side Feedback[J]. Journal of Zhejiang University SCIENCE C,2013,14(8):652-662.

顾新艳(1977-),女,汉族,江苏常州人,南京工程学院讲师,工学硕士,主要从事电子电气自动化方面的教学与研究,zdhxgxiny@njit.edu.cn。
Design of a Novel Digital Sampling Algorithm for Primary Side Regulation Flyback Converter*
GU Xinyan1*,CHENG Songlin2,WANG chong2
(1.School ofAutomotive and Rail Transit,Nanjing Institute of Technology,Nanjing 211167,China;2.National ASIC System Engineering Research Center,Southeast University,Nanjing 210096,China)
A new digital sampling control method is proposed in order to achieve high precision for primary side regulation flyback converter.The output voltage error can be received from the auxiliary winding of the transformer,and then can be used in the internal control loop to keep the output voltage stable.Compared to traditional digital sampling method,ADC or DAC is neglected in order to reduce the spending of circuit and power.Based on simulation,a 5 V/1 A AC-DC prototype of PSR flyback converter is used to verify the validity of the proposed sampling method. The voltage accuracy of constant voltage regulation reaches 0.5%.Which indicated that the algorithm has good realtime sampling,accuracy and practicablity.
flyback converter;digital sampling;voltage error;primary side regulation
TM464.62
A
1005-9490(2016)03-0644-06
EEACC:7210G10.3969/j.issn.1005-9490.2016.03.028

