基于模拟扩展法的高精度时间间隔测量电路设计

高　帅，刘烈曙，张　杰

(1．北京卫星导航中心，北京 100094；2．中船重工第七〇九研究所，湖北 武汉 430074；3．中国科学院 测量与地球物理研究所，湖北 武汉 430074)



基于模拟扩展法的高精度时间间隔测量电路设计

高帅1，刘烈曙2，张杰3

(1．北京卫星导航中心，北京 100094；2．中船重工第七〇九研究所，湖北 武汉 430074；3．中国科学院 测量与地球物理研究所，湖北 武汉 430074)

模拟扩展法是常用的高精度时间间隔测量的方法之一,基于模拟扩展法的高精度时间间隔测量电路，能够实现亚ns级的测量。模拟扩展法在实现过程中存在诸多问题，包括测量时间过长对用户使用产生影响、死区时间使测量误差增大、扩展系数标定影响测量精度等。针对每个问题分别进行机理分析，给出解决的方法。在实际时间同步系统中，对电路的性能进行了测试，结果表明测量精度可优于0.5 ns。

模拟扩展法；高精度；时间间隔测量

0　引言

高精度时间间隔测量，一般通过时间间隔测量系统实现。而时间间隔测量电路是时间间隔测量系统的关键部分，它决定了系统的测量精度。模拟扩展法是高精度时间间隔测量方法的一种。其发展历史悠久，应用范围较广[1]：19世纪80年代实现了亚纳秒量级的时间间隔测量；1998年Kari Maatta等实现了单次测量精度优于15 ps[2]；1999年Keunoh Park等实现分辨率为7.8 ps、精度为14.1 ps[3]；国内的相关研究机构于2000年左右实现测量分辨率优于100 ps、测量精度优于300 ps；目前采用模拟扩展技术和AD转换技术的时间间隔测量方法(TAC)精度可达几个ps。

模拟扩展法具有精度高、实现成本低的特点，但在具体实现中诸如死区时间、测量时间和扩展系数标定等问题，会极大地影响测量结果。本文对模拟扩展法的原理和误差进行了分析，对实现中的问题进行了分析解决，并在实际系统中进行了验证。

1　时间间隔测量原理

时钟脉冲填充法[4]是实现时间间隔测量最简单的方法，主要通过计数器实现：被测时间间隔连接到计数器的使能端，在整个被测时间间隔ΔT内时钟计数器不断计数，其计数值与参考时钟周期的乘积等于被测时间间隔。测量分辨率(LSB)等于参考时钟的周期(Tref)。由于参考时钟周期一般不会与待测时间间隔成整数倍关系，且相位也不可能完全一致，因此直接计数法的误差为±Tref。

根据测量原理，本地参考时钟周期决定了时钟脉冲填充法测量的分辨率，理论上参考时钟频率越高，测量分辨率就越高。但随着参考时钟频率的增加，电路实现复杂程度和成本将大大增加，且由于时钟抖动等因素引入额外的测量误差也将增加。因此，为了提高测量精度，除了对待测时间间隔进行参考时钟的整数周期计数外，还需精确测量不足1个参考时钟周期的时间间隔。目前常用的高精度时间间隔测量的方法很多，各种测量方法的比较如表1所示[2-8]，不同的使用要求和不同的环境，选择最适合的方法。

表1　各种时间间隔测量方法比较

2　模拟扩展法测量原理及误差分析

2.1测量原理

模拟扩展法基本原理为：对于大于整数时钟周期，采用时钟脉冲填充方法；对于小于1个时钟周期的时间间隔，利用此时间间隔对电容充电，通过一个时间常数比充电回路大许多倍的放电回路放电，将小时间间隔扩展至便于测量的大时间间隔。调整充放电的时间间隔长度以调整扩展系数。由于小时间间隔已经被扩展，因此能用相同频率的参考时钟对扩展后时间间隔进行计数，从而实现高精度时间间隔测量。此方法是基于电容的充放电的模拟电路将小时间间隔进行扩展，因此称为模拟扩展法[9-11]。

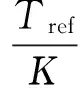
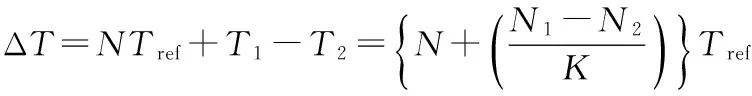
(1)

式中，N1为对KT1时间间隔测量得到的参考时钟整周期计数；N2为对KT2时间间隔测量得到的参考时钟的周期计数；K为时间间隔扩展系数。

2.2测量误差分析

由于待测时间间隔的上升沿和下降沿与本地时钟相位是随机且不相关的，因此计数器测量误差范围为±1个测量时钟周期。待测时间间隔上升沿(下降沿)在一个时钟周期内是等概率分布的，且计数器时间间隔测量的计数值符合二项分布规律。开始、结束信号的上升(下降)沿与参考时钟的上升沿之间存在一个小于参考时钟整数周期的相位差(T1、T2)，且该相位差是随机的。T1、T2的测量精度决定了系统的测量精度。T1、T2扩展了K倍，相当于将参考时钟频率提高了K倍，时间间隔ΔΤ可表示为:

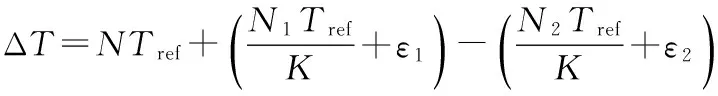
(2)

测量分辨率随着系数k增加而提高，与扩展系数成反比，与参考时钟周期成正比。待测时间间隔触发脉冲的上升沿与本地参考时钟是独立不相关的，故在分辨率内时间间隔触发脉冲认为是等概率均匀分布的。可以得到分辨率的量化误差标准差公式为：

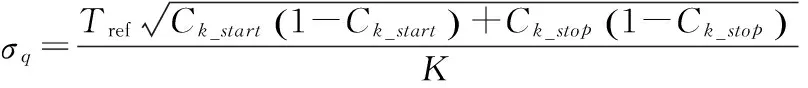
(3)

式中，Ck_start和Ck_stop分别是小于1个整周期时间间隔对应的开始触发信号和结束触发信号的上升沿(下降沿)在一个时钟周期中的分布概率。

3　基于模拟扩展法时间间隔测量电路的设计

3.1电路设计

基于模拟扩展法的高精度时间间隔测量电路设计如图1所示。图1中，PULS_IN为待测脉冲；V_OUT为输出电压；U1为运算放大器；U2为模拟开关；C1为扩展电容；Vref为基准电压；VCC为电源正；VDD为电源负；D1为钳位二极管，以保证相对稳定的电容起始充电电压。初始时刻，待测脉冲控制模拟开关U2对扩展电容C1的充电，R1控制电容的充电电流，使电容上的最大电压不饱和并处于线性范围内；R2控制电容漏电流的大小以调整电容充放电的比例，即转换系数；运放U1用于对电容充电以保证充电电流的稳定。

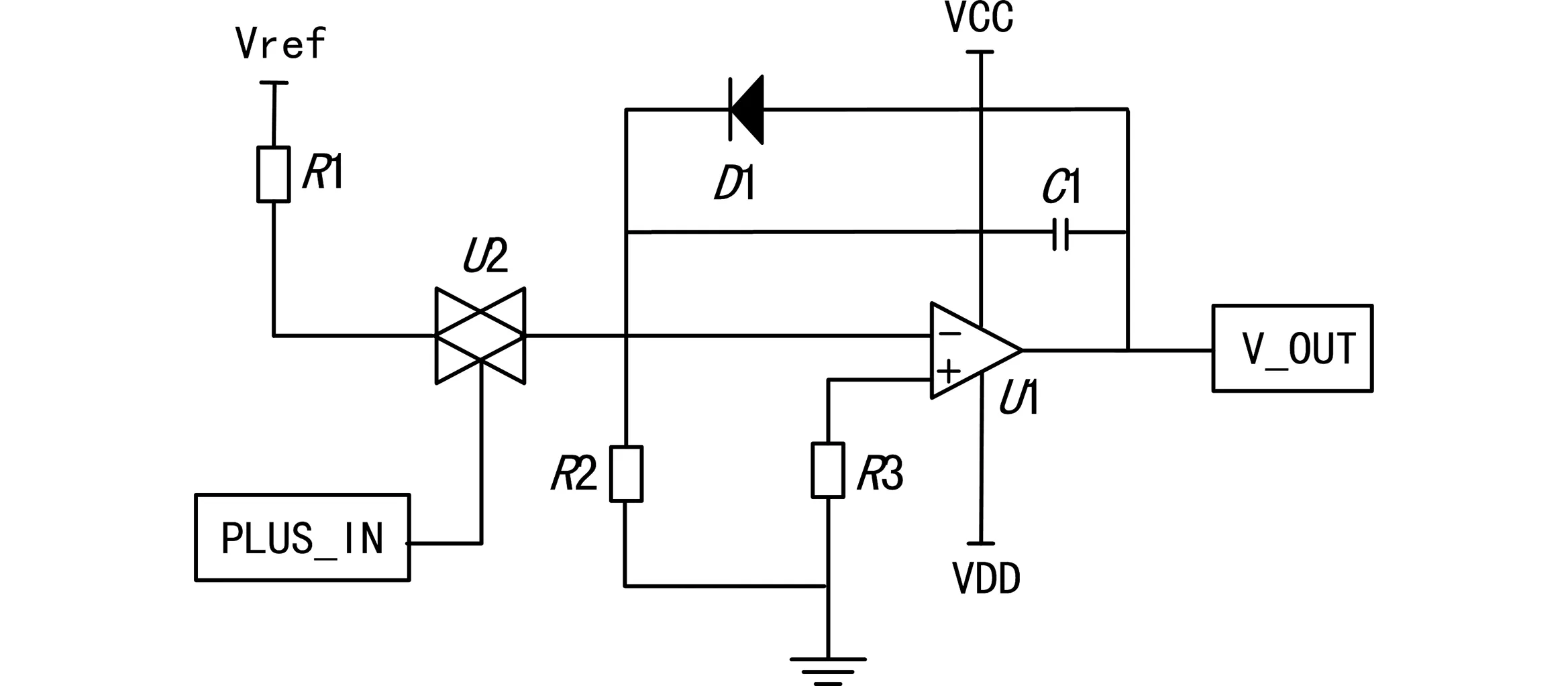
图1　基于模拟扩展法的高精度时间间隔测量电路

3.2电路实现中问题分析及解决

3.2.1测量时间

由于扩展后的时间间隔比原时间扩展了K倍(如1 000倍)，系统整体测量时间较长(原测量时间的K倍)。在实际使用中，如此长的测量时间是用户不能容忍的。根据原理，由于充电电容的电压与充电时间有关，充电时间越长，电容上的电压越高，因此可通过测量电容上电压的方法来代替测量电容的放电时间长度，并根据电容电压变化量与测量时间的关系计算整体的时间，这样就可以缩短实际的测量时间。需要注意到是，在电容完成充电后，暂时切断放电回路，使电容电压保持在最终的电压状态，待ADC测量完成后，再对电容进行放电，并进行测量。

采取此种方法的前提是电容放电电压的变化与测量时间呈良好的线性关系，这就需要通过调整电路参数，使电容工作于线性区域。例如对电容进行放电，电容电压变化2 V时，与之对应的时间间隔为40 ns，则电压变化与时间间隔对应的函数斜率为20 ns/V。则可认为在电容放电过程中，电压变化与时间间隔呈良好的线性关系，可利用此线性关系计算电容放电所对应的时间间隔，从而提高测量速度。

对于电容放电电压与时间间隔的的线性特性，笔者进行了专门的实验：以100 ns为周期，每10 ns为一个测量窗口，测量窗口内记录放电过程中电容的电压变化。如图2所示线性拟合误差可优于0.1 ns。因此线性拟合误差可以忽略不计。

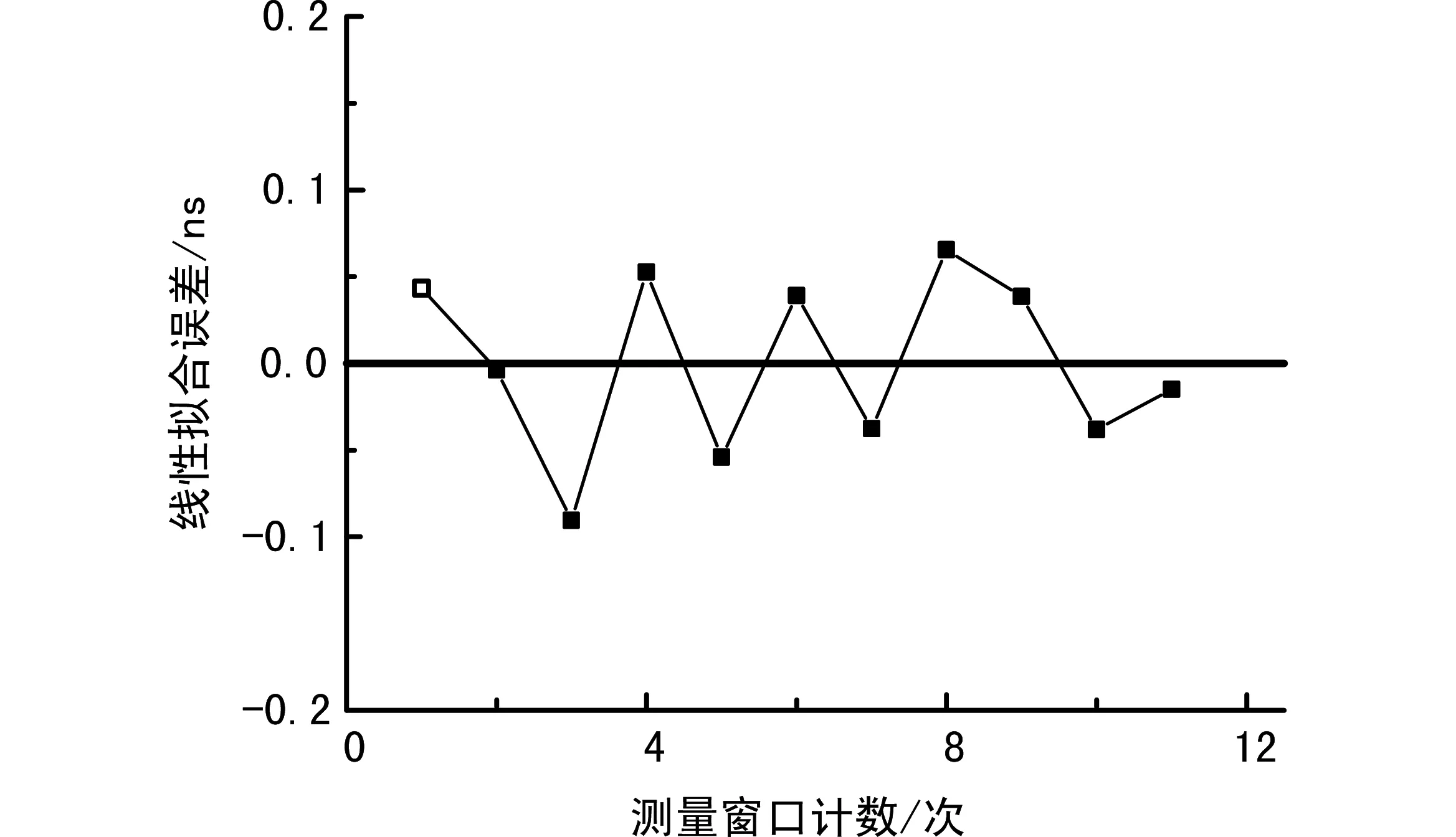
图2　电容放电电压变化与时间间隔线性拟合误差

3.2.2死区时间

死区时间是指电子器件的响应时间，即器件导通关断的延迟现象。一般来说死区时间是不可以避免的，且不可改变，只取决于电子器件制作工艺和材料等。如图3所示，A为待测时间脉冲，B为理想情况下的电容上的充电电压的变化，E是死区时间，D是实际情况下存在死区时间时电容上的电压变化，C是参考时钟。时间脉冲的上升沿由待测脉冲决定，其下降沿由测量时钟决定。理想状态下，A的上升沿出现同时电容开始充电，B的电压发生变化。而在实际过程中，由于死区时间的影响，在A上升沿出现的同时，电容没有开始充电，而是延迟了时间E后再开始充电，电容上的电压不能真实反映待测时间间隔。

极限状态下，如果待测脉冲宽度小于死区时间宽度，则电容上就无充电响应。这样就会产生测量误差。如图4所示，A和B都是待测时间脉冲，其宽度都小于死区时间宽度E，D是参考时钟，此时电容上电压C不会产生充电响应。

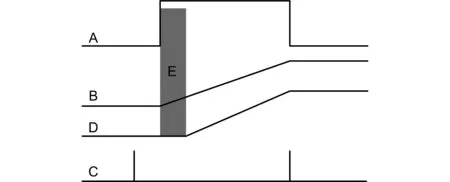
图3　死区时间示意

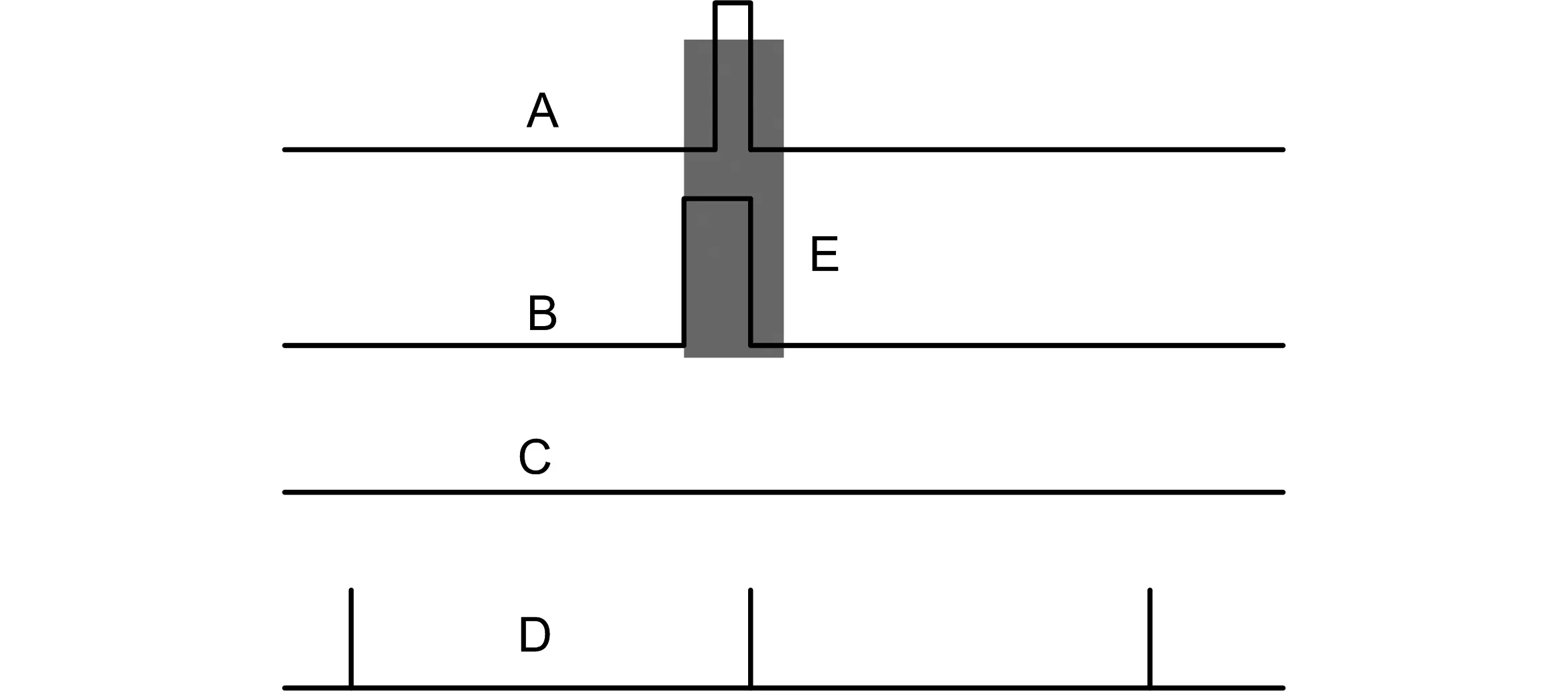
图4　电容充电电压无响应

为了避免死区时间的影响，可以将待测脉冲的下降沿再延长1个参考时钟周期，如图5所示。一般电容的死区时间约为ns量级，若本地参考时钟周期为100 ns(10 MHz)，则延长1个参考时钟周期已经能够完全避免由于死区时间的影响导致电容无法充电的现象。即使待测脉冲的上升沿与测量时钟的上升沿非常接近(小于死区时间)，也不会使电容上电压无响应。

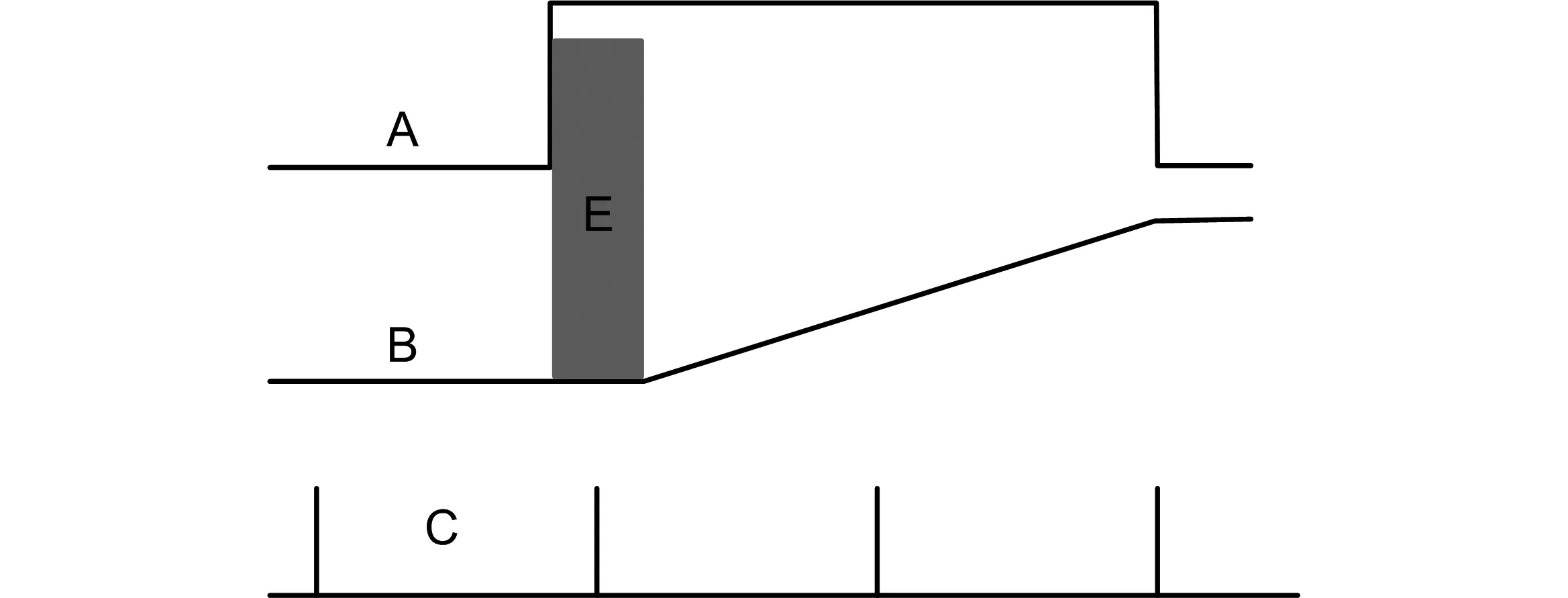
图5　延长1个参考时钟周期后避免死区时间的影响

3.2.3扩展系数

基于模拟扩展法的时间间隔测量电路的器件，易受环境变化的影响，因此测量误差也受到环境的变化影响。环境因素的影响主要体现在扩展系数上，当环境变化时，实际的扩展系数与标称值已经不同，此时的测量结果误差也将增大。

在进行每一次测量时，都相应的对系统的扩展系数进行标定，以提高单次测量测量精度。由于单次测量过程时间很短，环境变化对系统测量影响很小，此时的扩展系数能够代表当时的系统状态。单此标定的扩展系数参与当次测量，以提高测量的精度。扩展系数标定方法与解决测量时间过长的方法类似，通过测量电容上的电压的方法来代替测量电容的放电时间长度，并根据电容电压变化量与测量时间间隔的线性对应关系来标定扩展系数。前提条件是电容充/放电电压的变化与测量时间呈良好的线性关系，并使电容工作于线性区域。在测量时，为提高测量精度，利用已知脉冲宽度的校准脉冲来进行标定，即利用已知长度的“尺子”标定对应的电压变化。

但是在实际应用中，由于校准脉冲的产生机理，难以利用单个校准脉冲准确进行标定。校准脉冲往往由原子钟输出的频率信号为基准生成，由于脉冲生成电路的影响，实际生成的脉冲并不是理想脉冲信号，存在过冲、抖动等误差影响，生成的脉冲的宽度并不完全与标称值严格一致，导致标定扩展系数时存在误差。由于“尺子”(校准脉冲)本身不准确，因此也不能准确标定转换系数。同时由于测量电路存在死区时间，也会大大影响校准的准确度。

为了克服以上问题，采用2次校准的方法。如图6所示，第1次校准利用1个校准脉冲周期，记录对应的电压变化量；第2次校准利用2个连续的校准脉冲周期，记录相应的电压变化量。这2次校准的时间分别为1个和2个校准脉冲周期，再对这2次校准做差，则差值为1个准确的校准脉冲周期。因为在做差过程中，会将校准脉冲公共的误差消除(时钟抖动、过冲和死区时间等)，得到准确的时钟脉冲周期。相应的电压变化量差值就是1个准确的校准时钟周期内电压的变化。

如图6所示，C为电容上电压变化，B为脉冲宽度为T的校准时钟脉冲。首先利用一个时钟周期T测量电容电压变化量ΔV1，再利用连续2个校准时钟周期2T测量电容电压变化量ΔV2，则1个准确的校准脉冲周期内，电压的变化为ΔV2-ΔV1。

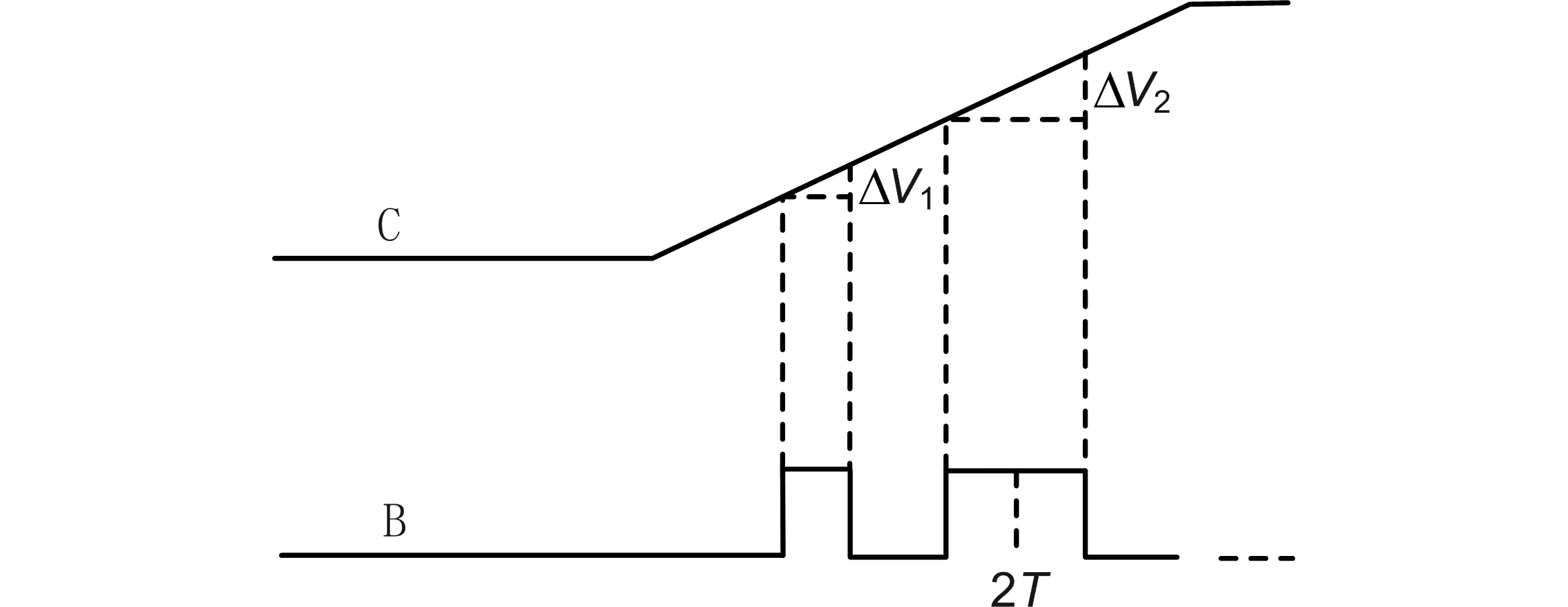
图6　利用2个连续校准时钟周期标定扩展系数

4　时间间隔测量电路性能测试

基于模拟扩展法的时间间隔测量电路可与FPGA及其控制器一起安排在一小块电路板上，组成一个时间间隔测量模块，测量精度可优于0.5 ns。

测试过程如下：A、B分别为2个站点，A为主站，B为从站。初始时刻，A站与B站时间进行同步。以A站为基准，实时测量A站与B站之间的时间差。超出预设门限后，及时对B站时间进行修正补偿，使之与A站时间严格同步。采用基于模拟扩展法的时间间隔测量模块(采用一阶电容扩展，扩展系数为1 000)，对两站输出的1 pps信号进行测量(1 pps信号可代表本地时间)。测试结果如图7所示，24 h测量时间内，对B站1 pps信号相位的平均补偿值为0.393 ns，均方差为0.369 ns，最大补偿值2.1 ns，最小补偿值-1.1 ns。

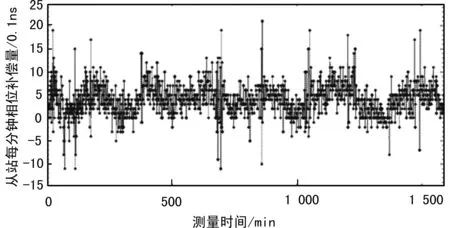
图7　测量结果

同时利用示波器器长余辉模式观察A、B站之间同步误差数据，如图8所示(图8中横轴每格表示为2.5 ns)。波形1和波形2分别代表2个站输出的1 pps信号。数据记录时间约为24 h，测量精度约为0.42 ns。

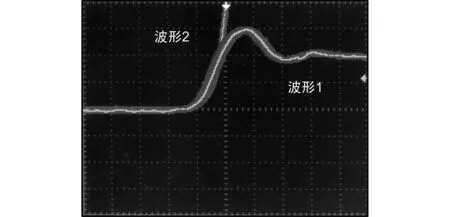
图8　示波器测量示意

5　结束语

基于模拟扩展法的高精度时间间隔测量方法，能够以较低的成本实现较高的精度。本文方法可以实现快速测量和避免死区时间等影响，并可以准确、快速地标定电路扩展系数。

在实际应用中，多采用一阶扩展的方法。因为二阶以上的高阶扩展中，参考时钟抖动误差已经与测量分辨率相当，或者大于测量分辨率，此时测量已经没有意义了；扩展系数与充放电电流比值有关，扩展系数越大，非线性因素影响也将随之放大，需要电路设计人员根据实际选择适合的扩展系数；此方法容易受到外界环境和工作条件的影响，在本文电路设计的基础之上，对温度等因素引起的误差进行补偿，可进一步提高测量精度。诸如以上都是在电路设计时需要注意的方面。

[1]张延，黄佩诚.高精度时间间隔测量技术与方法 [J].天文学进展，2006，24(1):195-197.

[2]MAATTA K,KOSTAMOVAARA J.A High-Precision Time-to-Digital Converter for Pulsed Time-of-Flight Laser Radar Applications[J].IEEE Transactions on Instrumentation and Measurement,1998,47(2):521-536.

[3]PARK K,PARK J.Time-to-digital Converter of Very High Pulse Stretching Ratio for Digital Storage Oscilloscopes[J].Review of Scientific Instruments,1999,70(2):1 568-1 574.

[4]KALISZ J.Review of Methods for Time Interval Measurements with Picosecond Resolution[J].Metrologia,2004(41):17-32.

[5]周渭，王海.时频测控技术的发展[J].时间频率学报，2003，26(2):87-95.

[6]SONG Jian,AN Qi,LIU Shu-bin.A High-Resolution Time-to-Digital Converter Implemented in Field Programmable Gate Arrays[J].IEEE Transactions on Nuclear Science,2006,53(1):236-241.

[7]TAMBORINI D.TDC with 1.5 % DNL based on a Single-Stage Vernier Delay-Loop Fine Interpolation[C]∥2013 IEEE Nordic-Mediterranean Workshop onTime-to-Digital Converters (NoMe TDC),2013:1-6.

[8]DAIGNEAULT M A,DAVID J P.A High-Resolution Time-to-Digital Converter on FPGA Using Dynamic Reconfiguration[J].IEEE Transactions on Instrumentation and Measurement,2011,60(6):2 070-2 079.

[9]KOSTAMOVAARA J,MYLLYLA R.Time-to-digital Converter with an Analog Interpolation Circuit[J].Rev.Sci.Instrum,1986,57(11):2 880-2 885.

[10]赵侃，梁双有，陈法喜，等.精密时间间隔计数器的研制[J].中国科学：物理学 力学 天文学，2011，41(5):602-606.

[11]车震平.一种高精度、大量程时间间隔计数器的设计[J].核电子学与探测技术，2011，31(6)：598-600.

[12]王希.高分辨率数字计时器(TDC)的设计与实现[D].武汉：华中科技大学， 2007：11-12.

[13]韩虹.基于TDC的事件计时器设 [D].上海：中国科学院上海天文台， 2006：16-17.

[14]杜燕，龚大亮，翟鸿飞.一种机动式时间频率传递系统设计与实现[J].无线电工程，2014,44(2):67-69.

[15]邢燕.高精度时间间隔测量系统[J].电子测量技术，2010,33(5):1-3.

[16]孙杰，潘继飞.高精度时间间隔测量方法综述[J].计算机测量与控制，2007，15(2)：145-148.

高帅男，(1982—)，硕士，工程师。主要研究方向：卫星导航和时间频率。

刘烈曙女，(1976—)，工程师。主要研究方向：时间频率。

Design of High-precision Time-interval-measurement Circuit Based on Simulation Stretch

GAO Shuai1,LIU Lie-shu2,ZHANG Jie3

(1.BeijingSatelliteNavigationCenter,Beijing100094,China;2.The709thResearchInstitute,ChinaShipbuildingIndustryCorporation,WuhanHubei430074,China;3.InstituteofGeodesyandGeophysics,ChineseAcademyofSciences,WuhanHubei430074,China)

The simulation stretch is one of the commonly used methods for high-precision time-interval-measurement.It can implement under ns level measurement.There are some problems in the process of implementation,such as long-measurement time,dead-zone and calibration of stretch-coefficient.The paper analyzes these problems and gives the solution.The performance of the time-interval-measurement module is tested in an actual time synchronization system.The results show that the measurement precision is better than 0.5 ns.

simulation stretch;high precision;time interval measurement

10.3969/j.issn.1003-3106.2016.08.18

2016-05-10

TP391.4

A

1003-3106(2016)08-0074-05

引用格式：高帅，刘烈曙，张杰.基于模拟扩展法的高精度时间间隔测量电路设计[J].无线电工程,2016,46(8):74-78.