一种噪声雷达地杂波消除算法

靳晓艳，李　伟

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.空军驻石家庄地区军代室，河北 石家庄 050081)



一种噪声雷达地杂波消除算法

靳晓艳1，李伟2

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.空军驻石家庄地区军代室，河北 石家庄 050081)

噪声雷达因其优异的抗干扰性能和低截获概率，在军事和民用领域均具有着巨大的应用潜力。针对噪声雷达地杂波消除困难的问题，提出了一种基于杂波基向量正交化的算法，该算法通过将接收信号输入格形滤波器，并自适应地调整滤波器的参数，以适应地面杂波未知的或随时间变换的统计特性，从而实现最优滤波。仿真结果表明，所提算法不仅对地杂波具有很好的消除效果，与此同时也能够有效抑制直达波。

噪声雷达；地杂波；格形滤波器；正交化

0　引言

噪声雷达指的是一类使用随机或伪随机波形信号来探测目标的雷达。在文献[1-3]中，这种雷达也被称为随机信号雷达(RSR)。噪声雷达的应用非常广泛，可以被用来进行目标监测、跟踪、引导、碰撞告警和地下勘测等。与传统的脉冲雷达、脉冲多普勒雷达以及调频连续波雷达相比，噪声雷达具有一些优点：噪声波形信号不会出现距离多普勒模糊，具有较低的峰值功率，与同频段的其他设备具有较好的电磁兼容性。归功于低峰值功率，噪声雷达也具有较好的电子反对抗能力，这种雷达被监听的概率很低，即使探测信号被检测到，也依然很难被判断为威胁信号。

然而噪声雷达的信号处理较传统雷达更为复杂，尤其对于杂波信号的消除，更是噪声雷达面临的挑战。来自雷达附近的强地杂波会增加信号处理中的噪底，甚至使得雷达接收机达到饱和。在典型的脉冲雷达中，有2种方法被用于消除地杂波：① 灵敏度时间控制(Sensitivity Time Control，STC)[4]，是通过使雷达接收机的灵敏度随时间(对应距离)变化，从而使被放大的雷达回波强度与距离无关；② 减弱地杂波影响方法是文献[5-7]介绍的经典动目标检测和动目标显示(MTD/MTI)技术，即接收信号通过带通或高通滤波器来消除零多普勒频率回波。文献[8]中说明了上述2种方法并不适用于噪声雷达，这是因为STC方法不能有效地消除地杂波的旁瓣，而简单的MTD处理也无法消除遮蔽效应。因此，对于噪声雷达来说，为了消除地杂波信号及其旁瓣，需要使用更复杂的自适应消除过程[9]。

本文提出一种基于杂波基向量正交化的地杂波消除算法，通过将接收信号输入格形滤波器，借助滤波器参数的自适应调整，实现地杂波的有效消除。文中首先分析了地杂波的信号模型，然后在线性空间内对杂波消除过程进行了分析，提出了基于格形滤波的杂波基正交化的方法，最后对所提算法的地杂波消除效果进行了仿真验证。

1　问题模型

含有地杂波的接收信号(没有运动目标)可以表示为：

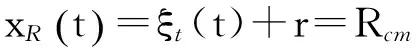
(1)

式中，ξt(t)为接收机热噪声；A(r)表示地杂波复振幅的距离分布；Rcm表示地杂波的最大距离(受地球的几何结构和发射信号功率的限制)。假设接收信号频谱是带限的，可以进行时间采样，采样周期为Ts<1/B，B为发射信号带宽。采样产生的离散时间信号可以表示为：

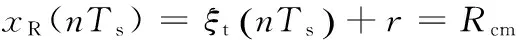
(2)

当地杂波反射率基本恒定不变的情况下，采样定理同样适用于空间域。假设式(2)表示的地杂波分布在等距离的点上[10]：

(3)

在这种假设下，地杂波信号的模型可以改写为如下形式：

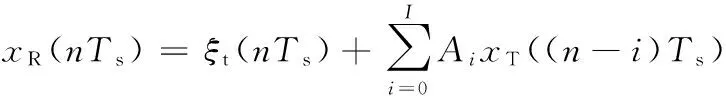
(4)

(5)

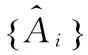
2　地杂波消除算法

采用线性空间的概念来考虑杂波消除过程。在多维信号空间中，接收信号可以看作是一个独立的点。该线性空间的维数是N(处理后的数据块中接收或参考信号的样本数)，通常该维数在105～107之间。消除杂波的过程是基于将信号空间分解为2个子空间，即杂波和目标子空间。在这种情况下，消除杂波最直接的方法是将接收信号投影到目标子空间上。但是，这种方法很难实现，因为目标子空间的维数很大。替代的方法是计算接收信号和杂波信号的减法从而得到无杂波的测量信号，只包含接收机热噪声和目标回波。杂波子空间的维度通常在102～104之间，一般远小于目标子空间的维数。因此，计算接收信号在杂波子空间上的投影就要简单的多，如图1所示。这种投影可以等效为杂波信号的估计，但计算量却能够明显减小。

图1　接收信号在杂波子空间上的投影

上述过程可以用式(6)来描述：

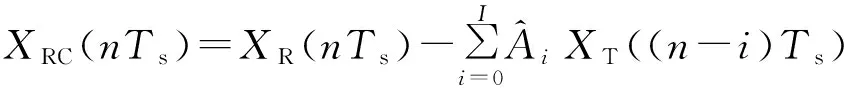
(6)

在观测时间无限长时，具有不同时移的噪声信号之间彼此互相正交。在这种情况下，可以简单地使用信号在每个杂波基向量上的正交投影，如图2所示。

然而在实际情况中，观测时间往往是有限的，致使构成杂波子空间的向量并非正交基。所以需要使用更复杂的杂波抑制算法来达到目的。其中一种方法是解式(5)所述的线性方程组；另一种方法是通过对杂波基向量进行线性变换来形成正交基向量。一种将杂波基向量正交化的方法是使用Gram-Schmidt正交化[11]，然而这种方法效率相当低，因为它需要I(I-1)/2次向量投影和减法，只有在I很小时该方法才适用。

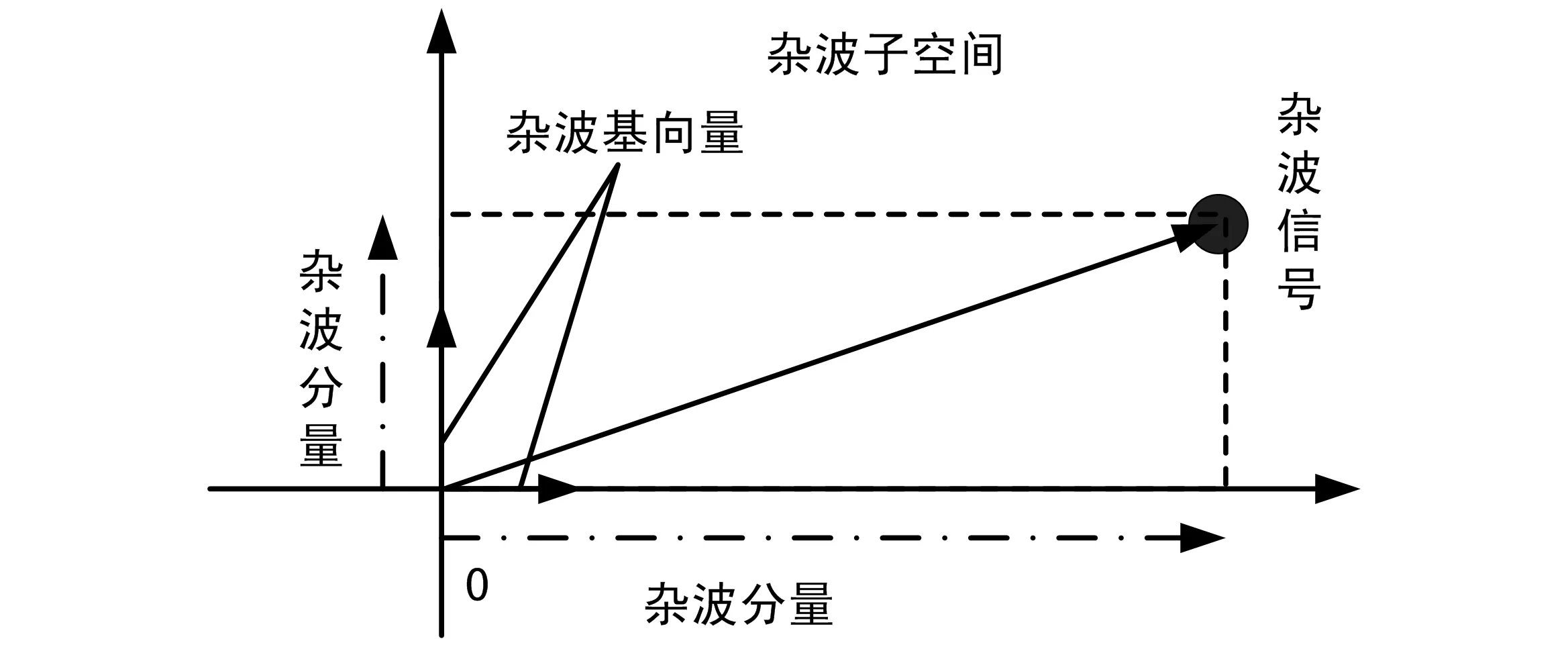
图2　信号在杂波的正交基向量上的投影

这里提出一种基于格形滤波器的杂波基向量正交化方法，如图3所示。这种方法较前面的方法需要的计算量小得多。格型滤波器结构由于其对有限字长效应具有很强的鲁棒性而被应用于很多实时性要求较高的场合，如汽车、机器人、雷达和交流电机等，相关内容可参考文献[12-15]。

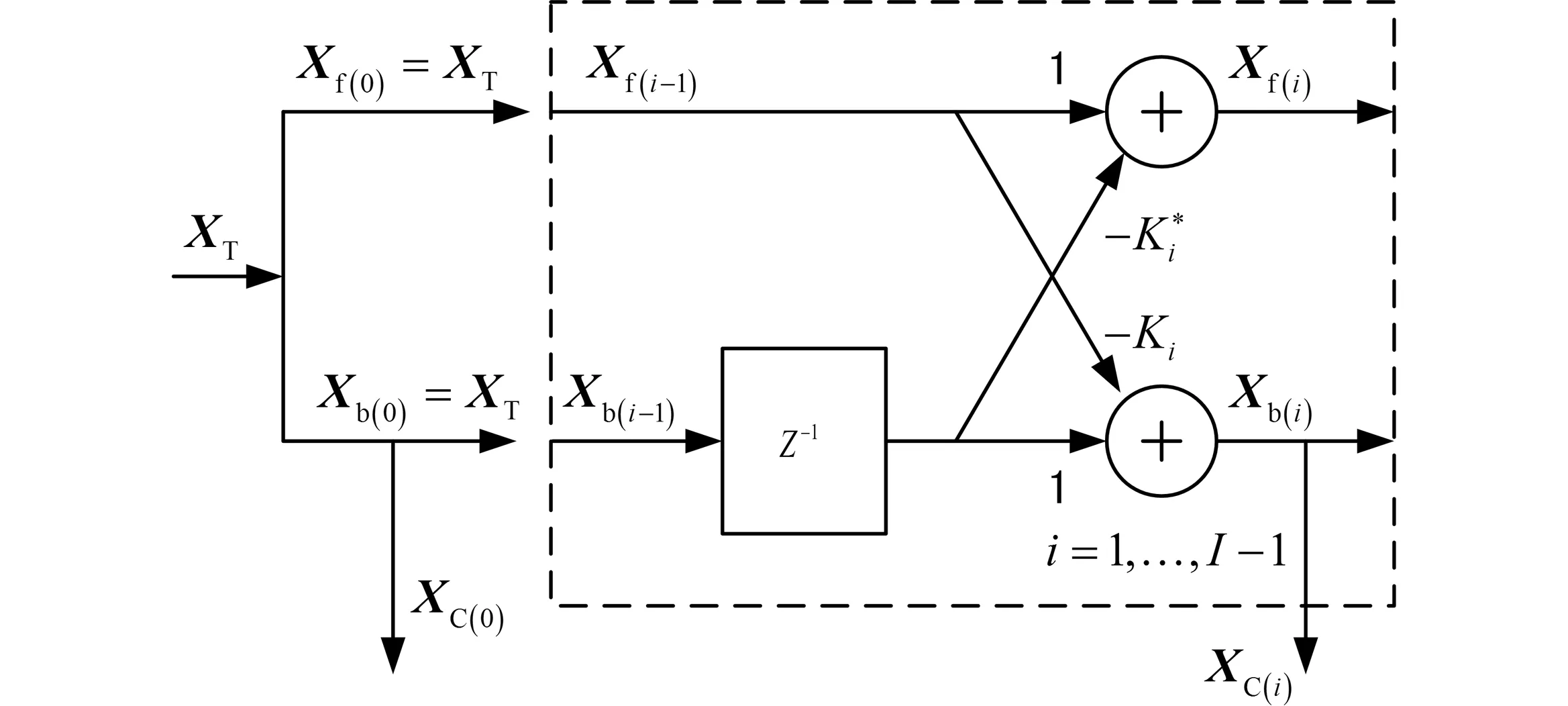
图3　基于格形滤波器的杂波子空间正交化

图3所示的格形滤波器包括I-1个相同的双乘法器格形单元，依据前面的状态(Xb(i-1)和Xb(t-1))，来产生后向(Xb(i))和前向(Xf(i))预测误差向量。在第一阶段的2个输入中，使用了发射(参考)信号向量XT。

格形滤波器从连续状态中得到的后向预测误差是互相正交的，因此桥型结构可以用于杂波基向量的正交化。每个状态的偏相关系数可以用下述公式计算：

(7)

前向预测误差信号Xf(i)可以用式(8)[10]来计算：

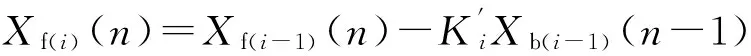
(8)

后向预测误差信号Xb(i)可以用式(9)来计算：

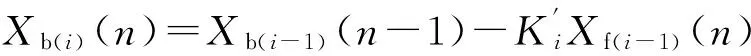
(9)

后向预测误差信号构成了杂波正交基向量：

XC(i)(n)=Xb(i)(n),i=0…I-1。

(10)

这些正交基向量进一步被用于消除接收信号中的杂波。可以用式(10)描述：

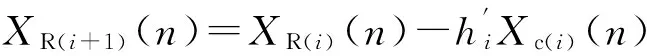
(11)

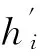
(12)

3　仿真分析

地杂波消除的仿真结果如图4、图5和图6所示。接收信号包含直达波(高出接收机噪声30dB)、几个地杂波信号(高出接收机噪声0～20dB)、一个15km处强烈的运动目标回波(S/N=-16dB)和一个27km处微弱的运动目标回波(S/N=-16dB)。

图4　接收信号的距离-多普勒相关结果

接收信号的距离-多普勒相关处理结果如图4所示。只有直达波和强地杂波是可见的，强杂波掩盖了运动目标的回波，致使目标不可见。传统的MTD/MTI处理结果如图5所示，过滤了零频分量。同地杂波一样，直达波也被过滤掉了，但是经过处理后的噪底保持不变。使用经典的MTD/MTI方法可以抑制地杂波，但不能抑制地杂波的旁瓣，因此微弱目标依然被地杂波的旁瓣所掩盖。采用本文提出的地杂波消除处理方法对接收信号进行处理的结果如图6所示。由图6可知，该方法可以有效消除直达波、地杂波及其旁瓣。该情况下，处理中的噪底有所降低，这时2个运动目标回波都能清楚的看到，由此验证了本文所提算法的有效性。

图5　MTD/MTI处理后的距离-多普勒相关结果

图6　本文算法处理后的距离-多普勒相关结果

4　结束语

本文通过对线性空间内接收信号所对应的目标子空间和杂波子空间的维数进行分析，得出了计算接收信号在杂波子空间上的投影更加简便的结论，并针对实际情况中杂波基向量并非正交的问题，提出了基于格形滤波的杂波基向量正交化方法。在对接收信号进行滤波时，通过自适应改变滤波器系数，对地杂波能够起到很好的抑制作用。此外，本文所提算法也能有效消除直达波。

[1]KULPA K S，CZEKALA Z，SMOLARCZYK M.Long-time-integration Noise Surveillance Radar[C]∥First International Workshop on the Noise Radar Technology(NRTW-2002)，2002:238-243.

[2]MALANOWSKIM，KULPA K.Detection of Moving Targets with Continuous-Wave Noise Radar:Theory and Measurements[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50(9):3 502-3 509.

[3]MALANOWSKIM，ROSZKOWSKI P.Bistatic Noise Radar Using Locally Generated Reference Signal[C]∥2011 Proceedings In TernaTional Radar Symposium(IRS)，2011:544-549.

[4]KRYLOV GM.An Amplifier with Discretely Controllable Gain[J].Telecommunications and Radio Engineering，1993，48(6):133-134.

[5]洪丽娜,汪连栋,王立平.MTD雷达抗干扰性能分析[J].火力与指挥控制,2004,29(21):71-73.

[6]秦轶炜,孙元敏,杨文华,等.低空监视雷达复杂环境下的最优CFAR设计[J].无线电通信技术,2015,4(2):59-63.

[7]杜晓恒,秦顺友,任冀南,等.低副瓣气象雷达天线增益测量及误差分析[J].无线电通信技术，2014,40(5):51-53.

[8]KULPA K S，CZEKAA Z.Ground Clutter Suppression in Noise Radar[C]∥Proc.Int.Conf.RADAR 2004，Tou-louse，France，2004:236-245.

[9]MALANOWSKIM.Comparison of AdaptiveMethods for Clutter Removal in PCL Radar[C]∥Proc.of International Radar Symposium 2006，Krakow，Poland，2006:237-240.

[10]HAYESM H.Statistical Digital Signal Processing and Modeling[M].New York:John Wiley & Sons，1996.

[11]LI G，LIM Y C，HUAN G C G.Very Robust Low Complexity Lattice Filters[J].IEEE Transactions on Signal Proce-ssing，2010，58(12):6 093-6 104.

[12]许江湖,张明敏.基于Gram-Schmidt正交化算法的水下目标回波检测[J].海军工程大学学报,2006,18(1):89-93.

[13]MALANOWSKIM.Comparison of AdaptiveMethods for Clutter Removal in PCL Radar[C]∥Proc.of International Radar Symposium 2006，Krakow，Poland，2006:237-240.

[14]HUANG C G，LI G，XU Z X，et al.Design of Optimal Digital Lattice Filter Structures Based on Genetic Algorithm[J].Signal Processing(Elsevier)，2012,92(4):989-998.

[15]张世平,赵永平,张绍卿,等.一种改进的自适应格型陷波算法及其收敛性分析[J].电子学报,2004,32(2):338-341.

靳晓艳女，(1984—)，博士，工程师。主要研究方向：电子对抗。

李伟男，(1983—)，工程师。主要研究方向：信号与信息处理。

A Ground Clutter Cancellation Algorithm for Noise Radar

JIN Xiao-yan1，LI Wei2

(1.The54thResearchInstituteofCETC，ShijiazhuangHebei050081，China;2.MilitaryRepresentativeOfficeofPLAAirForceStationedinShijiazhuangRegion，ShijiazhuangHebei050081，China)

Due to its excellent anti-interference performance and low intercept rate，noise radar has great apply potential in both military and civilian fields.In solve the problem of ground clutter wave cancellation in noise radar，an algorithm based on clutter base orthogonalization is proposed.In this algorithm，receive signal is put into a lattice filter，in order to fit the unknown or time-varying statistics characteristic of the ground clutter.And the parameters of filter are adjusted adaptively.Simulation results indicate that the proposed algorithm not only provides good cancellation effect to the ground clutter，but also can effectively suppress the direct signal.

noise radar；ground clutter；lattice filter；orthogonalization

10.3969/j.issn.1003-3106.2016.08.09

2016-04-20

国家科技支撑项目(2014BAK02B04)。

TN911.7

A

1003-3106(2016)08-0034-04

引用格式：靳晓艳，李伟.一种噪声雷达地杂波消除算法[J].无线电工程,2016,46(8):34-37.