考虑车站等级的城际铁路列车停站方案研究
程碧荣,赵晓波(.五邑大学 轨道交通学院,广东 江门 5900;.广州港股份有限公司,广东 广州 5000)
考虑车站等级的城际铁路列车停站方案研究
程碧荣1,赵晓波2
(1.五邑大学 轨道交通学院,广东 江门 529020;2.广州港股份有限公司,广东 广州 510100)
城际铁路列车的停站方案应综合考虑沿线车站的客流需求、车站所处的地理位置、车站的软硬件条件等因素,这些因素往往无法量化.论文将上述因素对停站方案的影响体现至车站等级上,首先应用层次分析法划分车站等级,在此基础上,构建以停站次数最少为目标函数的非线性0-1规划模型.最后以某城际轨道交通线路为例,应用Lingo软件求解模型,结果表明模型在考虑车站等级的列车停站方案优化中适用性较好.
城际铁路;停站方案;车站等级;层次分析法;0-1规划
列车开行方案是城际铁路运输组织工作的基础,停站方案是列车开行方案的重要组成部分,它决定着列车开行方案的合理性和效率.传统停站方案的确定方法编制效率较低,不能确保满足客流需求,且主观性强、经验估计程度高,因此无法得到最优方案,并导致运能浪费、服务旅客水平低等问题.早期,国内外学者大都是在研究列车开行方案的基础上进行停站方案的研究.随着停站方案重要性的凸显,近年来,单独针对停站方案的研究逐渐增多.易敏[1]使用层次分析法(Analytic Hierarchy Process,AHP)和灰色关联度法划分车站节点等级,建立以旅行时间损失最小、列车空走距离最小为目标的停站方案模型.徐斌[2]运用灰色关联度分析法和信息熵法确定节点等级,建立以列车平均上座率均衡指数最小、旅客旅行时间损失最少为目标的模型,并使用遗传算法对多目标模型求解.冯旭杰等[3]建立以最短旅行时间、最少牵引能耗为目标的停站方案模型,以现有运输能力为约束条件进行研究.邓连波等[4]以客流广义出行费用最小为优化目标,建立列车停站方案优化模型,并设计相应的求解算法.Salzborn等[5]在进行车站分组的基础上,利用动态规划法构造出不同的列车停站方案,并从所有可能的停站方案中选择出较优的方案.
实际上,停站方案的确定还要考虑技术、经济、社会等因素的影响,如车站技术作业能力、车站客运设备设施布置、车站在线网中的作用以及车站所在城市的经济发展情况等.但这些因素大都难以量化.本文利用AHP将这些因素对停站方案的影响投射到车站等级上,在考虑车站等级的基础上,构建以车站服务频率、列车停站次数和OD(Origin-Destination)服务频率等为约束条件的城际铁路列车停站方案优化模型,并利用Lingo软件求解模型.
1 AHP划分车站等级
车站等级是决定停站方案的重要因素,在普通铁路中,车站按业务量、地理条件等因素划分为特等站、一等站、二等站、三等站、四等站、五等站[6].但对于服务于市域客流的城际铁路而言,车站等级的划分应综合考虑客流情况、车站技术条件、社会及经济等多方面因素的影响.AHP通过具体数据和主观判断计算出决策元素权重,综合考虑各因素对决策对象的影响[7].本文在建立车站重要度评价指标体系的基础上,运用AHP确定车站重要度指标值,并据此划分车站等级.
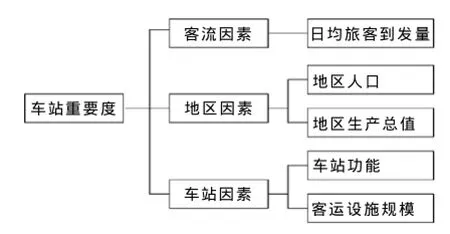
图1 车站重要度评价指标体系
影响车站重要程度的因素有很多,主要包括车站日均旅客到发量、客运设施规模、车站功能、车站所属地区经济发展状况、人口数量等因素.本文通过问卷调查、专家咨询等方式建立车站重要度评价指标体系,如图1所示.
根据图1所示的车站重要度评价指标体系,按照AHP的计算原理构造判断矩阵,并对构造的判断矩阵进行一致性检验,求出各车站的重要程度指标值,进而根据指标值的大小确定各车站的等级.一般可将车站划分为3个等级:一级车站、二级车站、三级车站.其中一级车站等级最高,包括线路端点站,以及线路上客流量大、地区经济水平高、人口数量多的车站.二级车站、三级车站重要性依次降低.
2 基于车站等级的停站模型构建
2.1 目标函数
列车的旅行时间由区间纯运行时分、列车起停附加时分和停站时间三部分组成.停站次数越多,列车的旅行时间就越长,列车的运行效率及乘客出行效率就越低.因此,在满足OD客流需求的前提下,列车开行方案的停站次数应越少越好,以此构建目标函数:

其中,ijx为列车i在车站 j停站与否的0-1变量,M为线路上开行的总列车数,N为线路的总车站数.
2.2 约束条件
城际铁路列车停站方案应满足车站到发客流与OD客流的需求,同时还需考虑车站等级以及列车等级对列车停站次数的限制.
1)车站服务频率
车站服务频率是指在一个周期内(一般指一天)列车通过某站点并服务该站点的次数[8].一般而言,车站等级越高其服务频率也越高,也能带给旅客更便捷的乘车体验.其计算公式如下:

其中, fi为停站方案中i站的车站服务频率; λmn为列车m是否在n站停车提供服务,若是则 λmn=1,否则 λmn=0.
车站总服务频率为全日列车在车站的停站次数总和,其应大于车站到发客流量中较大值的要求,即:

其中,jQ为车站 j的到发客流量的较大值,θ为列车平均满载率,P列为列车标准定员.
2)列车停站次数
列车的类型不同,其停站次数的约束也不同.为便于分析,将列车分为三类:直通列车、跨站停列车、站站停列车.其中,直通列车只停一级车站;跨站停列车除了停一级车站外,选停二级、三级车站;站站停列车在每个车站均停车.各类列车的停站次数约束如下:
直通列车:
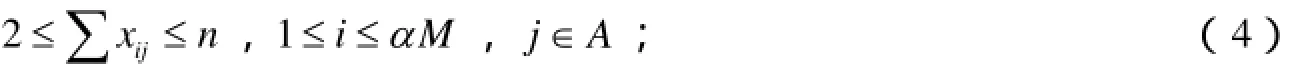
跨站停列车:

站站停列车:

其中,n为一级车站的个数;A为一级车站序号的集合; tΔ为线路各站起车附加时分加停车附加时分的平均值,即增加一次停站所带来的旅行时间的平均增加值;T为直达列车的旅行时间;T′为跨站停列车允许的最小旅行时间;T′为跨站停列车允许的最大旅行时间;α为直通列车的开行比例;β为站站停列车的开行比例.
3)站间服务频率
停站方案的实质是OD客流转化为车站节点间通达服务的过程[9].OD服务频率是指在起点到终点之间为旅客提供不换乘直达服务的列车对数.OD服务频率越高,说明服务于该起点到终点之间的列车越多,该起讫点的通达性越好.OD服务频率计算公式如下:

其中, fij表示车站i、 j之间的OD服务频率,若车站i与车站 j能够直达则 fij≥1,否则 fij= 0.
城际铁路乘客对于出行便捷性要求较高,若没有直达列车,则会选择其他更便捷的交通方式出行,因此本文不考虑乘客利用中转列车出行.站间服务频率应满足客流需求,即车站间开行的列车数应大于运送OD客流所需的列车开行数量.约束条件为:

其中,,j kQ 为 j站与k站之间的OD客流量.
4)变量约束
选取0-1变量描述列车i是否在车站 j停车:

5)始发站、终到站约束
在中短途城际铁路中,列车的运行径路和开行区段基本相同,本文假设所有列车的运行径路一致,均采用长交路方案,且所有列车在起始站与终到站均停站,即:

3 案例分析
以某城际铁路为例,该线路共设10个车站(分别记为A,B,,J… ),其等级划分:一级车站3个,分别为A站、F站、J站;二级车站3个,分别为C站、E站、H站;其余4个为三级车站.线路上所有列车的开行区段均为A站—J站.2015年A—J区段站间日均客流数据如表1所示.
线路上列车成对运行,主要考虑客流量较大方向的列车开行情况.由OD数据可知,该线路A—J方向客流量较大.由OD矩阵可计算出各区间断面客流量,并确定最大断面客流量为 A—J区间的12 339人.考虑线路的运营情况,全部开行CRH1B型动车组,列车定员1 299人,平均满载率95%,由此计算得 A—J区段应开行10趟列车.
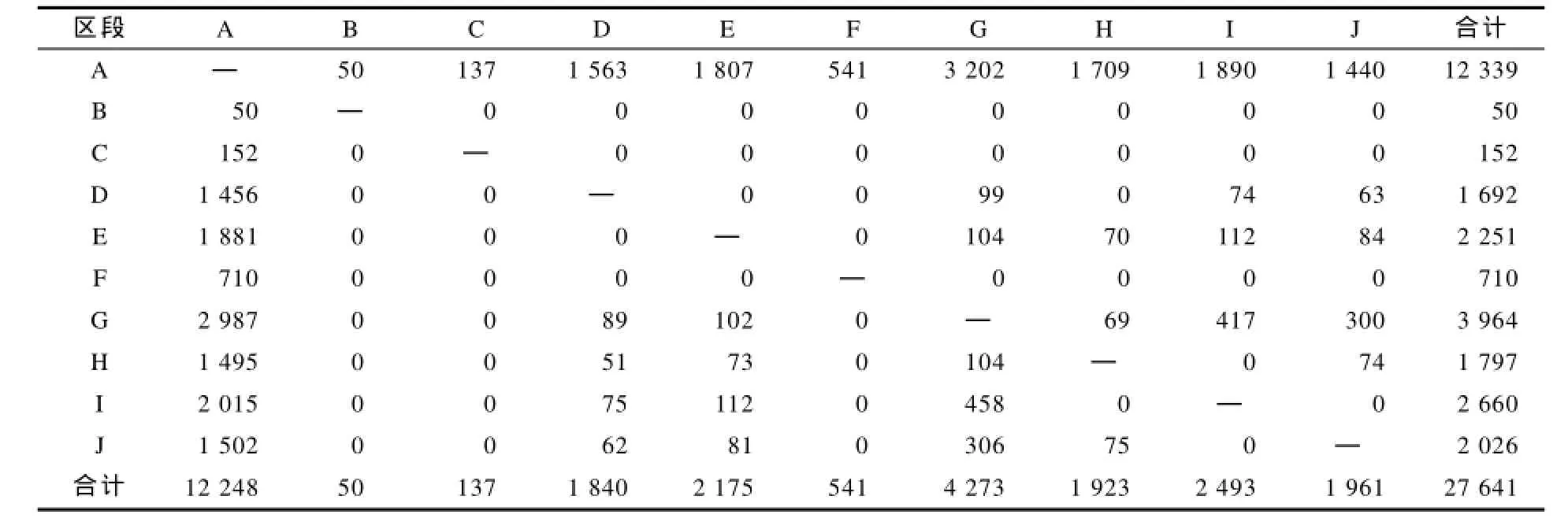
表 1A—J区段日均客流数据统计 单位:人
3.1 基于OD客流的停站方案
不考虑列车与车站等级对停站方案的约束,根据表1的客流数据,计算得该线路列车基于OD客流的停站方案(方案1)如表2所示.由结果可知,除了起点站与终到站外,其他车站的停站次数均较少,如一级车站F的停站次数仅为2次,无法体现该站在线路中的重要性.且方案存在列车停站次数过于集中的情况,不利于乘客的出行.
3.2 基于车站等级的停站方案
随着决策变量的增加,0-1规划问题求解的难度呈几何倍增.Lingo能用于求解线性规划、非线性规划、整数规划、二次规划等问题,具有模型表达简便、求解执行速度快等特点.对于车站数量较少的城际铁路系统,该软件具有较强的适应性.因此,本文选择Lingo软件进行模型求解.
为了保证商务客流的出行效率以及车站间的直达率,线路上要开行一定数量的直达列车和站站停列车,假定:直达列车开行比例 =0.2α,站站停列车开行比例 =0.1β ;该线路一级车站数量为3,直达列车仅在一级车站停站,因此要求直达列车停站次数不大于3;跨站停列车必须停一级车站,选停二级车站,因此停站次数应不小于3,为了保证跨站停列车乘客的出行效率,停站次数上限取6.同时,需对不同类型车站的服务频率进行约束,假定:一级车站服务频率不小于6,二级车站服务频率不小于3.
应用本文所构建的模型,利用Lingo软件求解得到基于车站等级的停站方案(方案2):A—J区段共开行直达列车2趟,跨站停列车7趟,站站停列车1趟(具体如表2所示).与方案1相比,方案2列车总停站次数较多,但同类型列车的停站次数相对均衡,各类型车站的服务频率与车站在线路中的重要程度基本匹配,故方案2相对合理.实际上,该停站方案优化模型能得到符合不同类型列车停站次数及不同等级车站服务频率要求的停站方案.
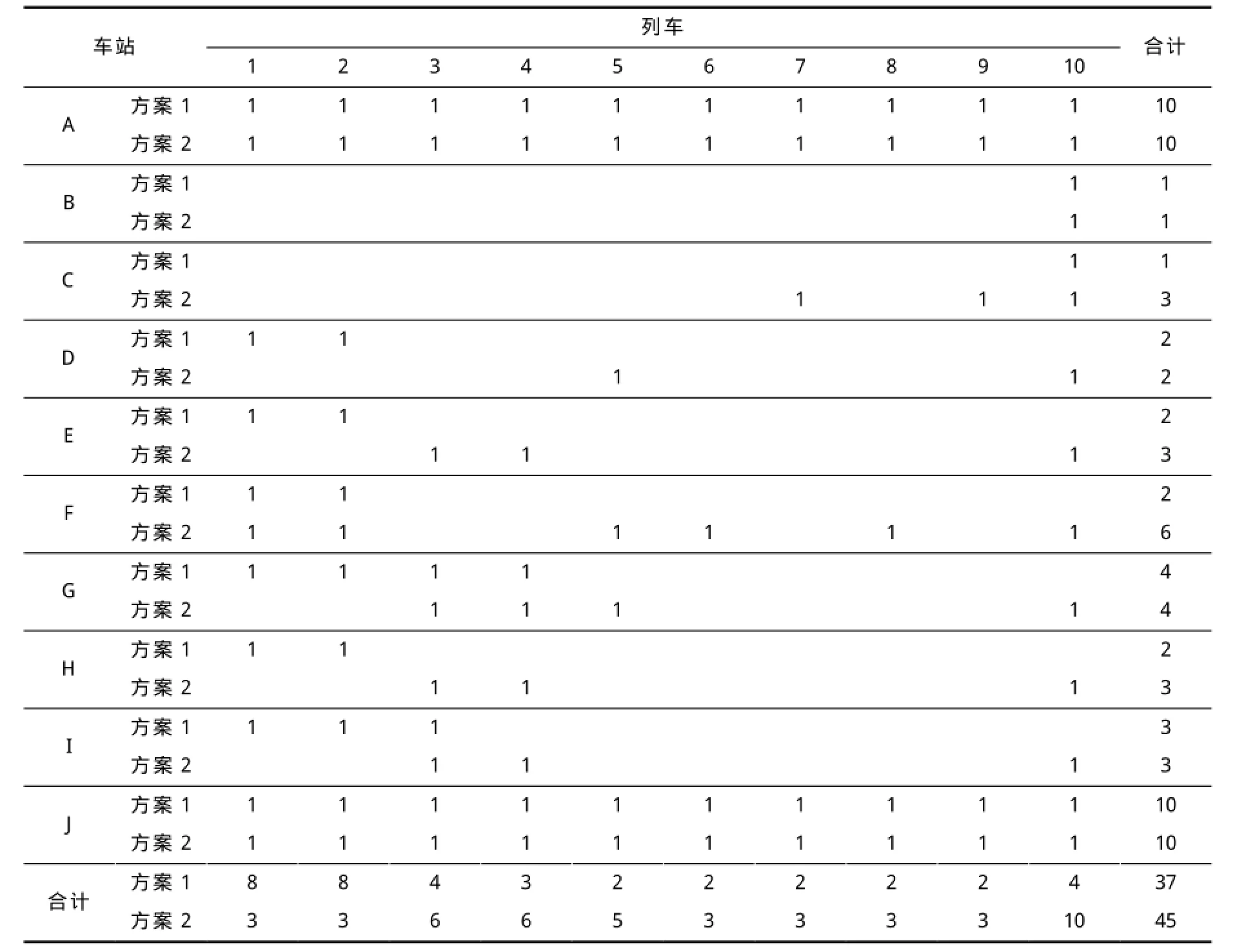
表2 基于OD客流数据(方案1)和车站等级(方案2)的列车停站方案
4 结论
在划分车站等级的基础上,本文构建了以总停站次数最少为优化目标,以车站服务频率、列车服务频率和站间OD服务频率为约束条件的城际铁路列车停站方案优化模型.结果表明,在考虑车站等级的基础上确定的停站方案,不仅能满足车站到发客流与OD客流的需求,还能提高线路重要车站覆盖率,均衡列车的停站次数.对于车站数量较少的城际铁路系统,该模型具有较强的适应性.但模型对列车停站次数均衡性的考虑不够,获得的结果存在停站类型过多的问题,不利于行车组织工作的实施;另外,对于车站数量较多的高速铁路系统,Lingo软件求解能力有限.解决这些问题将是下一步研究的方向.
[1]易敏.京沪高速铁路列车停站方案优化设计研究[D].成都:西南交通大学,2014.
[2]徐斌.高速铁路列车停站方案研究[D].北京:北京交通大学,2012.
[3]冯旭杰,孙全欣,冯佳,等.高速铁路既有停站方案优化模型[J].交通运输工程学报,2013,13(1):84-90.
[4]邓连波,史峰,周文梁.旅客列车停站设置方案优化[J].中国铁道科学,2009,30(4):102-107.
[5]SALZBORR E J M.The minimum fleet size for a suburban railway system[J].Transportation Science,1970, 4(4):383-402.
[6]梁东.中国路网铁路分类、分级研究[D].成都:西南交通大学,2010.
[7]汤代焱.运筹学[M].长沙:中南大学出版社,2002:236-244.
[8]徐鹏.城际客运专线列车开行方案研究[D].成都:西南交通大学,2010.
[9]徐瑞华,邹晓磊.客运专线列车开行方案的优化方法研究[J].同济大学学报,2005,33(12):1608-1611.
[责任编辑:熊玉涛]
A Study of Stop-schedule Plans for Inter-city Railway with Station Levels Taken into Consideration
CHENG Bi-rong1,ZHAO Xiao-bo2
(1.School of Railway Tracks and Transportation,Wuyi University,Jiangmen 529020,China; 2.Guangzhou Port Company Ltd,Guangzhou 510100,China)
When making stop-schedule plans for inter-city railways,traffic demands of the railway stations,their locations,and hardware and software conditions should be taken into consideration.These factors are hard to be quantified.This paper reflects the influence of the above factors on the level of stations.First,using the Analytic Hierarchy Process(AHP),stations are categorized into different levels.Then on the basis of this,the nonlinear 0-1 programming model is established by taking the minimum number of stops as object.In the end,taking a certain inter-city railway as example,the Lingo program is used to solve the model.The result shows that this model is of better practicabilityin the stop-schedule plan optimization with the levelofstations taken into consideration.
inter-city railways;stop-schedule plans;station levels;analytic hierarchy process;0-1 programming
U293.1
A
1006-7302(2016)03-0019-06
2016-03-17
程碧荣(1987—),女,湖南张家界人,助教,硕士,主要研究方向为交通运输规划与管理.

