铁路客运车站股道运用优化模型及算法研究
成利刚(五邑大学 轨道交通学院,广东 江门 529020)
铁路客运车站股道运用优化模型及算法研究
成利刚
(五邑大学 轨道交通学院,广东 江门 529020)
为了提高铁路客运车站的生产作业效率和自动化水平,本文通过对客运车站作业特点及股道运用计划的调查分析,以有效利用车站设备、提高车站接发车对数为目的,考虑车站接发车作业过程中的交叉干扰以及进路建立过程中的技术作业时间差,分别以股道占用时间和空费时间的方差来衡量股道运用的均衡性,建立了股道运用均衡的多目标模型,并用布谷鸟算法求解模型,以实际车站数据进行验证,结果证明了模型的可行性及优越性.
铁路客运站;股道运用均衡;交叉干扰;布谷鸟算法
随着铁路事业的发展,依靠通信技术、计算机技术等,铁路调度指挥自动化在一定程度上得以实现,列车严格按照运行图的规定在线路上运行.但对于铁路客运车站来说,运行图仅规定了列车在车站到达、出发、通过的时刻和停站时分,列车选择什么样的进路进站、在哪条股道停车、选择怎样的发车进路等只能由车站调度人员凭借自身经验安排,若赶上节假日车站的日接发车数量突然增大,调度人员将无法始终根据运行图和车站站场的时空约束来保证车站进路及股道的最优化配置,尤其是列车晚点时,车站股道不能按照原有计划进行安排,直接影响车站的接发车效率和服务质量.铁路客运车站如何制定合理的股道运用计划最大限度地提高接发车对数,成为亟待解决的问题.
车站股道运用不仅要得到列车在车站的到发时刻,还要得到列车在车站占用的股道.合理科学地解决铁路车站股道运用中存在的问题,不仅可以减少调度人员的工作量,提高进路安排的合理性,保证各设备的均衡使用,而且可以增加车站股道运用的抗干扰能力,提高车站服务质量.国内外学者对股道运用问题做了大量的研究.如Carey和Carville[1]以成本最小为目标,以最小时间间隔、多站台车站的站台占用以及进路交叉为约束条件的排序模型;雷定猷等[2]以车站设备的均衡使用、旅客乘降方便为目标的建模;谢楚农等[3]以方便旅客乘降和提升车站技术作业设备使用效率构建的多目标优化模型与分枝定界法的求解模型;Partha Chakroborty等[4]建立混合线性整数规划模型描述在列车到达不准时的条件下股道运用问题;乔瑞军等[5]以列车站内走行时间之和最小以及股道运用均衡为目标建模优化客运站股道运用;史峰等[6]以列车等级总权重最大化和到发线运用效用最大化为优化目标,对列车占用到发线和道岔进行相容性约束,建立了到发线运用和一端咽喉接发车进路排列方案综合优化的0-1规划模型.
本文主要从股道的均衡使用、提高设备利用率、减少列车在站内的走行时间、提高接发车的效率的角度,对车站股道运用进行优化.
1 模型建立
车站股道的总数量为M,该站开行的列车总数为N. xij( i∈ N, j∈ M )表示第i列列车对第j条股道的占用情况,若 xij= 1,则表示第 j条股道被列车i占用,占用的总时间为 tij,否则 xij= 0.表示列车i尾部越过股道 j相应方向出站信号机的时间,即列车i在 t时刻从股道 j出清;在列车i之后的任意列车k( k ∈ N )占用股道j的时间为t.则列车在车站的接发车及其他作业必须满足以下约束:
1)列车编组长度 li必须受到所占用股道有效长度的限制 Lj,即 Lj> li;
4)同一股道接发相邻列车的时间间隔要满足最小安全时间间隔要求,即其中, Δj为前行车i出清股道 j、后行车k准备并进入股道 j的最小时间;
5)任一列车在进行接发车作业占用咽喉区段时,应避免与其他列车的接发形成冲突[7].如果列车i办理股道j的接发车作业与列车k办理股道h的接发车作业存在交叉,则 Aik=1,否则 Aik=0;如果列车i办理股道 j接发车作业的进路与列车k办理股道h接发车作业的进路是平行作业,则Bijkh=1,否则 Bijkh= 0;因此,为了避免两列列车的进路存在时间交叉,则两列列车应安排平行进路,即必须满足:
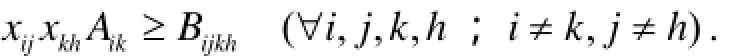
股道运用均衡主要指列车对每条股道的占用总时间的均衡和股道空费时间的均衡.通过均衡,最大限度提升车站的接发车能力以及股道运用方案的抗干扰性能.
以每条股道被占用时间的方差来衡量股道被占用总时间的均衡性,目标函数1f的函数值越小,表明每条股道的占用时间越均衡:

以进入同一股道的相邻列车间隔时间的平方和衡量股道占用间隔时间均衡.目标函数2f的函数值越小,表明同一股道的相邻列车间隔时间越小,这有利于提高股道的利用率,即提高车站的接发车能力.

目标函数:
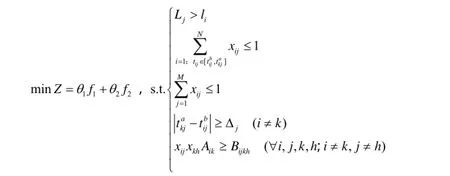
其中, θ1,θ2分别为目标函数 f1和 f2的权重系数,本文令 θ1=θ2= 0 .5; Tij为进入股道j的相邻两列列车的时间间隔.
2 布谷鸟算法
布谷鸟算法是剑桥大学学者Xin-She Yang和Suash Deb提出的一种启发式智能优化算法[8].该算法基于布谷鸟寻找鸟窝放置鸟蛋,并融入了鸟类的Lévy飞行行为,很好结合了局部随机过程和全局随机过程.与遗传算法、粒子群算法等相比,布谷鸟算法有更好的寻优速度和更高的精度[9-11],其局部随机过程可描述如下:
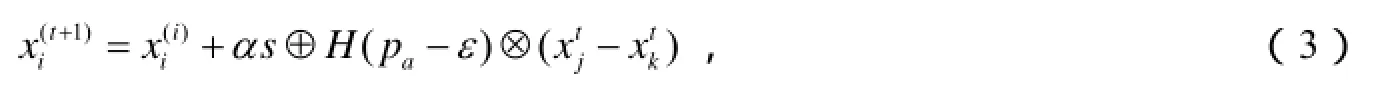
全局随机过程按Lévy进行,可表示为:

其中, s ≫ s0>0,1 < λ ≤3.
2.1 初始化种群
为缩短计算时间,本文求解时采用整数编码:按照列车占用股道的时间顺序将列车编号为1,2,3,…, N,车站股道编号为1,2,3,…, M.初始化种群数量只需包含所有列车,因此随机产生N个鸟窝位置 xi( i = 1,2,…,N ).
2.2 适应度函数选取
对于股道运用优化问题,以股道分配的均衡值最小作为其优化目标,本文以目标函数作为算法的适应度函数,即:
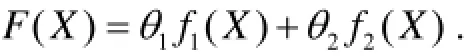
2.3 算法流程
布谷鸟算法的具体步骤如下:
步骤1 初始化m个鸟窝位置 xi( i = 1,2,…, m ),选出全局最优的鸟窝位置,并将其保留到下一代;
步骤2 用式(3)、式(4)进行鸟窝位置的更新,将适应度函数值与更新前进行对比,保留较好的鸟窝位置;
步骤3 抛弃较差的鸟窝.产生服从均匀分布的随机数 r ∈ ( 0,1),并与发现概率 pa= 0.25进行比较,如果 r > pa,则将改变,通过与步骤2得到的鸟窝位置对比,保留较好的鸟窝位置,并选出当代全局最优位置 X;
3 验证实例
本文以实际铁路客运枢纽站N站Z场进行验证,其平面布置图如图1所示,Z场中包括20~28 共9条股道,出站开行的方向主要有A、B和C 3个动车所.
目前,N站日均办理列车364.5对,其中营业列车283.5对,动车组出入库84.5对,上水列车54组,上水吸污列车19组,发送旅客117 567人,到达旅客107 955人;高峰期办理列车386对,其中营业列车294.5对,动车组出入库96.5对,上水列车61组,上水吸污列车23组,发送旅客130 195人,到达旅客134 723人.其中Z场每日开行列车69.5对,选取某日下午14:00到凌晨00:12这段时间进行研究,N站Z场的股道分配优化前方案如表1所示,可计算其股道均衡值 Z = 643.316 7.
根据模型的目标函数和约束条件,计算得到如表1所示的N站Z场的股道运用优化后方案,其运用均衡值 Z = 76.817 8,明显优于原方案.
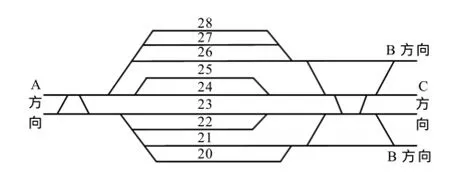
图1 N站Z场平面图
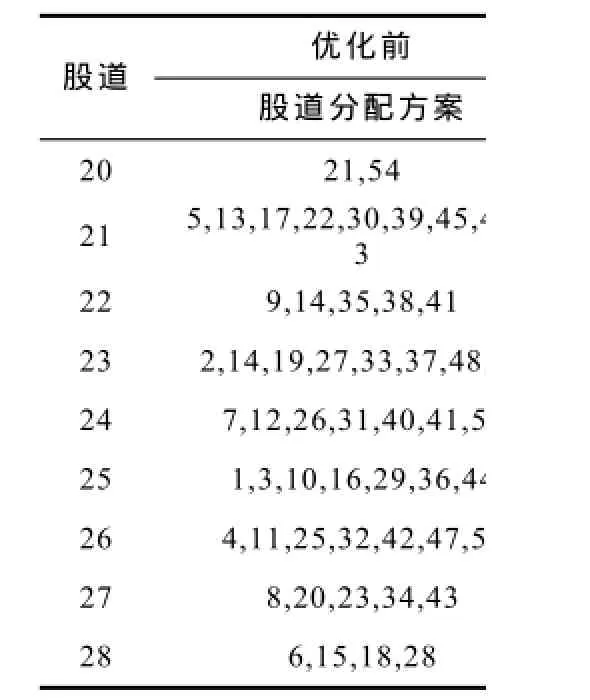
表1 优化前后,N站Z场的股道分配方案
4 结论
为了提高铁路客运车站股道运用计划编制的科学性和自动化水平,本文以股道运用均衡为目标建模,能够提高车站设备利用率和车站接发车能力;同时对于车站股道运用计划的抗干扰能力也有所改善;由于考虑了进路间的交叉干扰,使得模型更加符合实际.本文结果对于铁路客(货)运车站、铁路编组场以及城市轨道交通停车场股道运用计划的编制都有一定的借鉴意义.但在建模过程中,没有考虑车站的调车作业,也没有详细论述股道运用计划抗干扰能力的大小以及影响因素,无法对模型的实用性作出科学的评价,因此,本方案的使用有一定的局限性,只能应用于行车密度不是特别高的客运车站.
[1]CRAEY M,CRAVILLE S.Scheduling and platforming trains at busy complex stations[J].Transportation Research Part A,2003,37(3):195-224.
[2]雷定猷,王栋,刘明翔.客运站股道运用优化模型及算法[J].交通运输工程学报,2007,7(5):84-87.
[3]谢楚农,黎新华.铁路客运站到发线运用优化研究[J].中国铁道科学,2004,25(5):130-133.
[4]CHAKROBORTY P,VIKRAM D.Optimum assignment of trains to platforms under partial schedule compliance [J].Transportation Research Part B,2008,42:169-184.
[5]乔瑞军,朱晓宁,张天伟,等.客运专线车站接发车进路选择与调整问题研究[J].北京交通大学学报,2012,36(3):57-64.
[6]史峰,陈彦,秦进,等.铁路客运站到发线运用和接发车进路排列方案综合优化[J].中国铁道科学,2009,30(6):108-113.
[7]郭莉,吕红霞,陈焕云.基于遗传算法的铁路车站到发线运用优化研究[J].西南民族大学学报(自然科学版),2005,31(1):28-31.
[8]YANG Xinshe,DEB S.Cuckoo search via Lévy flights[C]//World Congress on Nature&Biologically Inspired Computing.Piscataway:IEEE Publications,2009:210-214.
[9]青学江,马国忠.遗传算法在区段站到发线的应用研究[J].西南交通大学学报,1998,33(4):30-40.
[10]李煜,马良.新型元启发式布谷鸟搜索算法[J].系统工程,2012,30(8):64-69.
[11]姚远远,叶春明.作业车间调度问题的布谷鸟搜索算法求解[J].计算机工程与应用,2015,51(5):255-260.
[责任编辑:熊玉涛]
A Study of the Optimization Model and Algorithm for Track Application in Railway Passenger Stations
CHENG Li-gang
(School of Railway Tracks and Transportation,Wuyi University,Jiangmen 529020,China)
In order to improve railway passenger stations’production efficiency and automation level, this paper,through an investigative analysis of passenger stations’operation characteristics and track use plans,with the efficient use of railway stations’equipment and increasing train departures and arrivals as the object,and taking into consideration the cross interference by arrivals and departures and the technical operation time difference in the approach process,measures the equilibriumof track use using the variance of the hold-up time and time unoccupied respectively,establishes a balanced multi-purpose model for track use,adopts a cuckoo algorithm,and validates the model against actual station data.The results prove the feasibility and superiority of the model.
railway passenger stations;track use equilibrium;cross interference;the cuckooalgorithm
U293.2
A
1006-7302(2016)03-0014-05
2016-03-18
江门市基础与理论科学研究类项目(20150030004128)
成利刚(1987—),男,甘肃天水人,助教,硕士,研究方向为交通信息工程及控制.

