中印股票市场资本配置效率比较研究

王淑坤，张延良（.山东财经大学 财务处，山东济南 5004；.山东财经大学 金融学院，山东 济南 5004）

中印股票市场资本配置效率比较研究

王淑坤1，张延良2
（1.山东财经大学 财务处，山东济南 250014；2.山东财经大学 金融学院，山东 济南 250014）

中国与印度都是处于转轨阶段的新兴市场经济体，印度股市140年的发展历史使其成为亚洲股票市场的典范，其资本配置功能发挥出色，存在许多可供中国参考借鉴之处。本研究在 Wurgler资本配置效率模型的基础上，选取了中国和印度股票市场近十年的相关数据，采用 Granger因果检验、VAR模型方法比较分析了中印两国股票市场的筹资额和经济增长之间的关系，研究发现，GDP和股票市场的筹资额在中印两个国家都存在长期均衡关系；印度股票市场的资本配置效率高于中国股票市场的资本配置效率。

股票市场；资本配置效率；Granger因果检验；VAR模型

0 引 言

作为金融市场重要组成部分的股票市场在经济发展中的地位越来越重要，股票市场的一个基础作用就是实现资本的优化配置，股票市场资本配置效率的高低直接决定了该国资本配置产生效果的大小。国家的发展程度不同导致各国的股票市场发展状况也不同，进一步导致股票市场的资本配置效率也各不相同。

印度的股票市场起源于孟买的股票非标准化交易，孟买证券交易所（BSE）于1875年成立，它是亚洲历史悠久的证券交易所，截止到2012年末，印度共有5191家上市公司进行股票交易，是全球上市公司最多的国家之一，印度很多重要的公司、企业都在孟买交易所上市。和其他发展中国家相比，印度股市是一个成熟的拥有上百年股票交易历史的市场。中国的股票市场虽然没有印度的历史悠久，但是它厚积薄发，迅速地踏入了快速发展的行列。1990年上交所和1991年深交所分别开业，标志着我国股票市场的正式成立，经过短短二十五年的发展，股票市场迅速发展，截止到2014年末中国共有2613家境内上市公司，和1990年成立之初的14家相比，扩大了上百倍，上市公司的质量明显提高，股票市场的资本配置能力得以提升。

中国与印度作为金砖五国中的两个主要成员国，均是处于转轨阶段的新兴市场经济体，两国的国民经济增长较快，有着巨大的发展潜力。正是在中印两国经济发展和合作过程中存在的共性使得两国在相关领域的比较研究成为学术界的一个热门话题，像“中印之争”、“龙象比较”等。印度股市上百年的历程是中国无法超越的，尤其是进入21世纪以来，印度股市经历了一轮迅速的发展，使其成为亚洲市场的典范。中国与印度在经济、政治等许多方面均具有共性，两国股票市场的发展也存在相互借鉴之处。两国股票市场的发展与合作正在引起学术界与实务界的关注。

1 国内外文献综述

资本配置通俗地讲就是资本的分配，资本配置广义的定义是指资本按照不同的来源组合，在不同的用途之间进行分配。资本配置效率通常被认为是：一定的技术条件下各种生产要素投入后，在各产出主体中所获得的生产效益，它有两层含义：一是资源在全社会的配置效率，主要靠国家经济制度完成；二是使用效率，这种效率是厂商利用生产要素进行生产来实现。现代经济学认为，正是资本的这种资源配置功能使得资金在各个行业流动，这种流动使得各个行业都能有所发展。本文所使用的资本配置效率和资源配置效率是同一个含义，本质上是相同的，通俗地讲就是资本通过股票市场流向产生较高收益率的行业或企业的能力。

1.1 国内学者关于资本配置效率的研究综述

我国大部分关于股票市场资本配置效率的研究都是在Wurgler模型的基础上进行的，只是他们选取的研究对象不同，有分地区的，有分行业的，但是核心思想是相同的。李志宾［1］以 GDP增长率和股市筹资额为指标从我国31省市、22个行业以及六大类企业三个方面分析了我国股票市场资本配置效率，研究表明资本在中国股票市场的配置效率比较低。吴阳［2］用大盘指数和投资额的变动按照不同行业验证了股票市场的资本配置效率，得出资本在中国股票市场的配置效率较低，最后作者提出了相应的改进措施。李名义等［3］以我国股票市场的总市值和上市公司EPS为数据指标，建立回归模型，研究了我国股票市场整体的资本配置效率。牛冬梅［4］按照行业分类，按照各个行业筹资额变化比率和利润变化率进行了线性回归，最后计算出了不同行业的资本配置效率，由此可以看出，我国股票市场整体的资本配置效率不好。李勇［5］也是分行业进行分析研究的，他把股票市场分为18个行业，然后分别以每个行业的成交额和利润额增长率为指标进行分析，并对模型进行单位根检验和Granger因果检验，最终得出我国股票市场整体资本配置效率比较低，但是这两个时间序列指标不存在协整关系，说明我国股票的成交额和利润率并没有明显的长期均衡关系。王锦慧等［6］在一级市场上选择上市公司IPO筹资额和该公司的平均利润率两个指标，二级市场选取股票的成交额和平均利润率两个指标，研究表明我国股票一级市场和二级市场的资源配置效率从1996-2005年都比较低，而且交易市场比发行市场的效率还要低，甚至有的年度为负效率。张婉霞［7］从基本面和技术面两个方面进行分析，基本面用可以量化的指标例如营业收入、净资产等，技术面由上市公司的月股票价格合成，这两个方面分别代表我国的实体经济和虚拟经济，并以两者之间的关系建立回归模型，对我国从2001-2009年各年的资本配置效率进行了研究。结果显示中国资本市场的资本配置效率相对低下，并呈现“波浪式”的非稳定趋势。同时，也反映了我国实体和虚拟两个经济部门在我国的发展不均衡、不协调，即实体经济没有给虚拟经济的发展打下夯实的基础，而虚拟经济也没有促进实体经济的发展。金雪军等［8］选取投资效果系数计算我国的资本配置效率，其中，投资效果系数=产出增量（用国民生产总值代替）/投资流量（全社会固定资产投资额）。万艳［9］从宏观和微观两个方面进行了研究。其中，微观方面主要从上市公司的角度即上市公司的增量资金（首次融资和再融资资金）使用效率和存量资金（并购重组）使用效率来分析；宏观方面主要从股票市场促进国家产业结构优化的效率情况和股票市场促进国家经济增长的效率情况两个角度来分析。实证分析结果表明，不管是在微观层面还是在宏观层面股票市场的资源配置效率都比较低。张立［10］以台湾证券交易所、柜台市场等构成的台湾多层次股票市场为研究对象，以上市公司的营业收入为自变量，以月度股票总成交额为被解释变量进行了回归分析。庞如超［11］以2002-2007年 20个行业的上市公司为样本，用行业股票市场筹资额和行业上市公司利润总额进行了实证回归分析，结果表明：比香港证券市场不足的是，上海证券市场和深圳证券市场根本没有很好地发挥出资本在市场上的配置功能，导致出现资金严重错配问题。

1.2 国外学者关于资本配置效率研究的研究综述

国外学者早在20世纪 90年代就开始对股票市场资本配置效率进行分析和讨论了。Wurgler［12］以37个发达国家和28个发展中国家共六十五个国家为研究对象，用整个社会行业固定资产和利润为指标研究了六十五个国家1963-1995年三十三年间的资本配置效率，结果表明：发达国家的平均资本配置效率值明显高于发展中国家的平均值，而且每一个发达国家的值都大于发展中国家的值，甚至有的发展中国家为零。Chari等［13］根据托宾 Q理论对资本匮乏国家的 369个企业在股票市场放开前和放开后的股本总额进行了研究，结果表明企业的股本在股票市场开放后比开放前增加了4.1%，但是作者只是做了基础研究，文章并没有系统地研究出资本消除障碍自由流动时是否能够提高资本配置效率。Galindo等［14］学者运用两种不同形式的资本边际预期收益选取十二个不同国家上市公司面板数据为研究对象，衡量了这些国家的资本配置效率，需要说明的是这12个国家均是发展中国家。作者使用两种方法来计算，一种叫作柯布道格拉斯生产函数计算法，另一种用营业利润除每单位投资额来计算资本配置效率。两种方法得到的结果都是一样的，所研究的对象整体上资本配置效率都不高。Ksiazek等［15］通过研究指出：股票价格随机漫步的特征在收入水平比较低的国家表现的比较明显，这说明股票价格并没有改善资本在微观经济中的配置作用。而且低收入国家的政权阶层经常通过独裁限制资本市场的独立发展，从而在很大程度上降低了资本配置效率；相反，高收入水平国家的证券市场的股票价格可以有效地传递信息，并能促进资本流向投资回报率高的项目。这一研究结果说明资本配置效率在不同的国家具有一定的差异性。Chong等［16］研究了巴西、印度、俄罗斯、中国等金砖四国股票市场的效率，作者主要参考了一些简单的技术指标，比如平均线、移动平均线、相对强弱指标、动量线等股票市场技术指标来比较金砖四国股票市场的效率，结果表明巴西的股票市场效率在金砖四个国家中最高，作者还分析了各国效率不同的原因。

本文以中印两国股票市场为研究对象，利用 Jeffrey Wurgler计算资本配置效率的模型来研究中印两国股票市场的资本配置效率。选取了中印两国股票市场的筹资额（包括首次公开发行、增发配股等方式的筹资额）和年度 GDP为指标在国家层面上进行实证分析，并比较中印两国股票市场资本配置效率的高低。

2 中印股票市场资本配置效率分析的变量与方法选择

2.1 变量的选取及数据来源

纵观国内外已有的研究，大多数都是以Wurgler模型为基础，只是在指标的选取上有所不同，有的学者以股票市场筹资额和 GDP为变量，有的学者以上市公司的总市值和上市公司平均每股收益为变量，还有的学者以股票市场的成交额和利润总额为变量。不管选择什么指标都是用模型的弹性系数表示资本配置效率，两者是正比例关系，若弹性系数数值较大则说明资本配置效率高，弹性系数数值较小则说明资本配置效率低。

本文以中国和印度股票市场为研究对象，计算中印两国股票市场资本配置效率，研究的是国家与国家之间股票市场的对比，所以本文选择的是股票市场的筹资额和 GDP，以股票市场筹资额为因变量（用 I来表示），以GDP为自变量（用G来表示）。即GDP增长越快的国家相应的股票市场筹集的资金就越多，从而说明该国股票市场的资本配置效率越高；相反，GDP增长越慢的国家相应的股票市场筹集的资金就越少，从而说明该国股票市场的资本配置效率越低。由于查阅数据各种条件的限制，本文使用的均是季度数据。同时还要对两组季度数据进行对数处理，主要是为了避免时间序列数据的剧烈变动从而消除序列的异方差性。

2.1.1 股票市场筹资额

本文所用的股票市场筹资额包括首次公开发行、增发、配股以及其他方式的筹资额的总和。数据来源于wind数据库，得到的是月度值，经过处理整理为季度值。图1和图 2分别表示中国和印度股票市场筹资额的走势，其中中国的数据选择的是2004-2014年，从走势图可以看出在开始的几年股票市场筹资额较少而且增减幅度较小，中间几年涨幅较大，波动也比较大，最近几年筹资额有所下降，但是从2013年9月起出现平稳回升的趋势。印度数据选择的是2004-2012年（到目前为止，wind数据库只更新到2013年3月份，所以本文的数据截止到2012年底），从走势图中可以看出，除了2011年第一季度有了较大增长外，其他时间一直保持着稳定增长的趋势，从而也进一步说明了印度股市的走势基本稳定。

图1 中国股票市场筹资额走势图（单位：亿元）

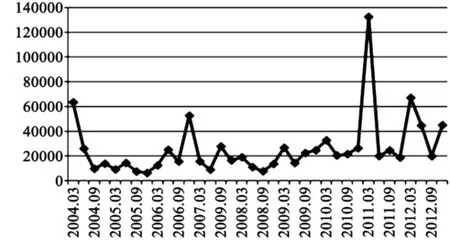
图 2 印度股票市场筹资额走势图（单位：千万卢比）

2.1.2 国内生产总值 GDP

wind数据库、国家统计局、世界银行等提供的国家GDP有年度数据和季度数据，考虑到样本的数量，本文选择的是季度GDP。图3和图4分别表示中国和印度 GDP走势。从两国的走势图可以看出近十年以来两国的 GDP呈稳定增长的趋势，说明两国的经济一直在平稳的增长。

图3 中国季度 GDP走势图（单位：亿元）

图 4 印度季度 GDP走势图（单位：千万卢比）

2.2 研究方法

由于本文的研究对象国内生产总值和股票市场筹资额都属于时间序列数据，因此我们采用动态时间序列模型进行分析。首先，进行单位根检验，进行单位根检验主要是为了消除“伪回归”，之所以出现“伪回归”是由于很多时间序列数据变量之间不存在相关性，但是它们都会随着时间的推移产生一个共同的趋势，从而产生一个看似有意义的回归系数，要从根本上消除“伪回归”就需要进行单位根检验。所以，我们在对时间序列变量进行回归分析时，要先检验序列的平稳性，如果时间序列不平稳则会出现“伪回归”的现象，这是就需要对数据进行下一步的处理。其次，进行协整检验，验证国家 GDP和股票市场筹资额之间是否存在长期的均衡关系。再次，进行Granger因果检验，用来验证股票市场筹资额和国家 GDP之间是否存在因果关系，如果存在因果关系则可进一步对两者进行建模分析。最后，构建VAR模型及进行脉冲响应分析，运用脉冲响应在建立VAR模型的基础上验证国家GDP的变动对股票市场筹资额的影响。本文的数据分析均用计量经济学软件Eview7.0完成。

3 中印两国股票市场资本配置效率分析

3.1 单位根检验

通常在实际中遇到的时间序列数据都是不平稳的，所以有必要在建立计量模型前对数据进行单位根检验。对时间序列数据I和 G分别取自然对数，可以消除两组变量自身所具有的异方差性，用 lnI和 lnG表示。在对时间数据序列的平稳性进行检验时，通常采用 ADF法来验证，通过对变量lnI和 lnG进行ADF检验来看其是否存在单位根，如果时间序列数据不存在单位根，则说明时间序列是平稳的；反之若存在单位根，则说明时间序列是不平稳的，需要对时间序列数据分别进行差分。如果时间序列数据经过差分处理后是平稳的，则可以进一步进行协整检验和Granger因果检验。在Eview7.0中，对中印两个国家的时间序列数据 lnI和lnG分别进行ADF检验。其中，I1、G1分别表示中国股票市场的筹资额和季度 GDP；I2、G2分别表示印度股票市场的筹资额和季度GDP。检验结果如表1所示。

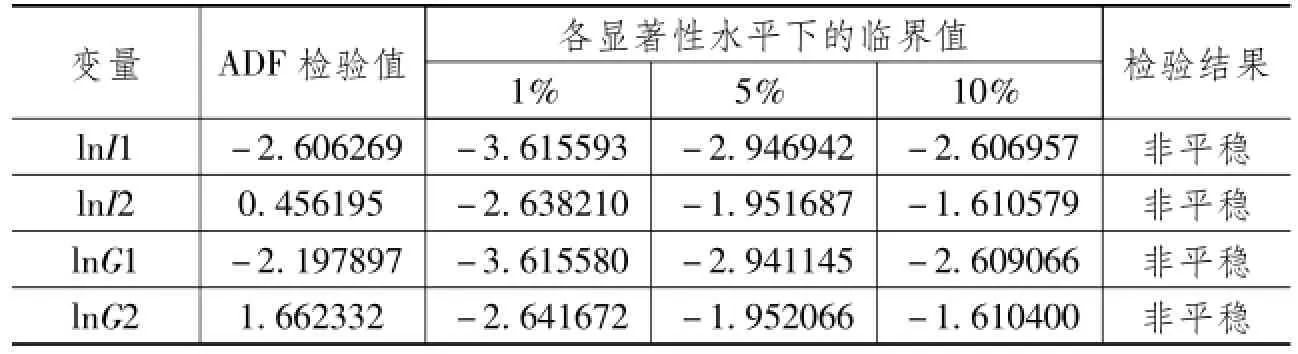
表 1 lnI和 lnG的 ADF检验结果

由表1可以看出，在1%、5%、10%三个显著性水平下，四个时间序列变量得到的单位根检验值均大于临界值，说明中印两国的lnI和lnG序列是非平稳的，然后进行差分，对各个差分变量进行 ADF检验。检验结果如表2所示。

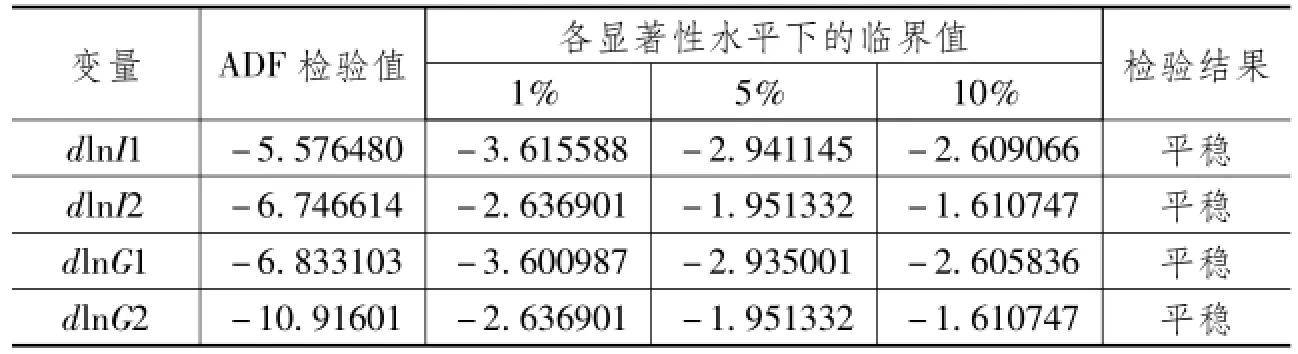
表2 dlnI和 dlnG的 ADF检验值

由表2可以看出在1%、5%、10%三个显著性水平下，四个差分时间序列数据 ADF检验值均小于临界值，说明两国时间序列变量是都是一阶单整的，由于它们都是同阶单整、满足协整检验的条件，因此我们可以进行协整检验。

3.2 协整检验

协整检验验证的是非平稳的时间序列是否存在长期的均衡关系，协整检验一般分为两种方法，一种叫做Johansen检验，这种方法检验的是回归系数，该方法常用于检验多个变量；还有一种是检验回归残差，这种方法又被叫做 E—G两步法，这种方法通常用于检验一元回归方程。本文使用的是简单一元回归方程，只有两个变量，所以使用的是E—G两步法。很多学者通过对国外成熟股票市场的研究发现，宏观经济和股市之间存在密切的关系，在成熟的股票市场上，这种关系尤其显著。

接下来对中印两国相关变量的时间序列进行协整检验。首先，建立回归方程：

然后利用最小二乘法对数据进行回归估计，得到方程的残差序列resid，将其残差序列定义为ET，即ET= resid，再对残差序列ET进行ADF检验，最后得到的结果如表3所示。

从表3可以看出，在 1%、5%、10%的显著性水平下，残差序列ET1和 ET2均为平稳序列，这说明两组变量均存在协整关系。也就是说中国和印度股票市场的筹资额与 GDP之间存在长期均衡关系，意味着 GDP的增长对股票市场的筹资额已经具备了稳定的内在影响机制。

表3 对残差项序列 ET的单位根检验结果

3.3 Granger因果检验

表 4 中国股票市场筹资额和 GDP的因果关系检验

Granger因果关系表示的是时间序列在时间上的先后顺序，只是时间上的因果关系，重在影响方面的确认，而非完全的因果关系。通过Granger检验，可以很容易地看出两个变量的因果关系。下面对中印两国的数据进行Granger因果检验，得到的结果如表4和表5所示。

由表4可知，当滞后期为3的时候，lnG不是lnI的原因的概率为0.0967，故在10%的显著性水平下拒绝原假设，说明 GDP增加是股票市场筹资额增加的 Granger原因，但是股票市场筹资额增加不是 GDP增加的Granger原因。同理，在滞后长度为4的情况下，得到的结论和在滞后期为3的情况下得到的结论相同。

表 5 印度股票市场筹资额和 GDP的因果检验

由表 5可知，当滞后期为 2期或者为3期的时候，lnG不是 lnI的原因的概率均小于 0.01，故在1%的显著性水平下拒绝原假设，即GDP的增加是股票市场筹资额增加的Granger原因，同时股票市场筹资额不是 GDP增加的 Granger原因。

3.4 VAR模型的构建及脉冲响应分析

3.4.1 VAR模型的构建

为了进一步研究 GDP的变动对股票市场筹资额的影响，在不区分解释变量、被解释变量的情况下，把两个变量放在同等的位置上进行向量自回归分析，即根据中印两国的数据构建 VAR模型，具体公式如下：

表6 中国 VAR模型最优滞后阶数的确定

首先用 eviews计量软件确定中印两国 VAR模型的最优滞后阶数，结果如表 6和7所示。由表 6可知中国VAR模型最优滞后阶数为 2，这与前文的Granger因果关系检验的最优滞后阶数是一致的；由表7可知印度 VAR模型最优滞后阶数为3，这与前文的 Granger因果关系检验的最优滞后阶数也是一致的。

3.4.2 脉冲响应

表7 印度VAR模型最优滞后阶数的确定

在VAR模型中，脉冲响应函数表示的是两个地位平等的变量，其中一个变量对另外一个变量的冲击或信息所做的反应。脉冲响应函数是建立在VAR模型稳定的基础之上，所以进行脉冲响应分析之前，要先确定 VAR模型的稳定性。如果VAR模型不稳定，就不能进行脉冲响应分析，因此我们先要检验中印两国VAR模型的稳定性。VAR模型的ADF检验如图5和图6所示。从图中可以看出，VAR模型的全部根的倒数值都在单位圆内，说明VAR模型满足稳定性条件，接下来可以进行脉冲响应分析。

VAR脉冲响应结果如图7和图8所示。其中，从图7可以看出中国GDP对股票市场筹资额的冲击开始较小且为负的冲击，在滞后1.5期时（大约 5、6个月时）负的冲击达到最大，然后缓慢减小，在滞后 2期以后（大约半年）冲击趋于平稳，说明当中国经济增长时，股票市场也相对活跃，从而导致股票市场的筹资额增加，而且这种影响不是暂时的；从图8可以看出印度GDP对股票市场的冲击也是明显的，都是正的冲击，而且也是在滞后1.5期（大约5、6个月时）冲击达到最大，在滞后3期以后冲击趋于平稳，说明印度的经济增长带动股票市场的发展。中印两国的VAR脉冲响应结果均很好地反映了经济增长对股票市场筹资额的影响。

图5 中国VAR模型的稳定性检验

图 6 印度 VAR模型的稳定性检验

图7 中国VAR脉冲响应结果

图8 印度脉冲响应结果

4 研究结论

本文采用了单位根检验、协整检验和 Granger因果检验、VAR模型检验等处理非平稳时间序列的分析方法，对中印两国股票市场筹资额与GDP之间的关系进行了实证分析，通过实证结果，得出以下四个结论：

第一，从回归方程的弹性系数来看，印度股票市场的资本配置效率大于中国股票市场的资本配置效率。对中国的数据进行分析，得到中国股票市场资本配置效率为0.92，说明当中国的GDP增加1%时，股票市场的筹资额增加0.92%；对印度的数据进行分析得到印度股票市场资本配置效率为1.64，说明当印度的GDP增加1%时，股票市场的筹资额增加1.64%。仅仅比较弹性系数，可以看出印度股票市场的资本配置效率远远大于中国股票市场的资本配置效率。

第二，从中印两国所选数据的平稳性和协整性来看，两国的 GDP和股票市场的筹资额都存在长期均衡关系。通过对两国所选数据序列进行ADF检验，结果中印两国的 GDP序列都是非平稳序列，经过一阶差分后都稳定，中印股票市场筹资额时间序列也都是非平稳的序列，经过一阶差分后均平稳，说明这四组变量都是一阶单整，而且是同阶单整。通过对中印两国回归方程的残差分别进行 ADF检验，得出残差序列均不存在单位根，说明他们都是平稳序列，也就是说两国的GDP和股票市场的筹资额都存在协整关系即两个指标在中印两个国家都存在长期均衡关系。

第三，从Granger因果关系来看，印度股票市场的资本配置效率比中国股票市场的资本配置效率要高。就中国而言，GDP和股票市场筹资额的因果关系不是非常明显，在 10%的显著性水平下 lnG是 lnI的 Granger原因；就印度而言，GDP和股票市场筹资额的因果关系相对明显一些，在1%的显著性水平下lnG是lnI的Granger原因。通过 Granger因果检验，表明两国的股票市场的筹资额都随着 GDP的增长而增加，只是印度因果关系比较明显，在1%的水平下显著，这也进一步说明印度股票市场的资本配置效率比中国股票市场的资本配置效率要高。

最后，从 VAR模型检验以及脉冲响应结果可以看出，一国 GDP的增长能引起股票市场筹资额的变动，正好也说明了股票市场是一国经济的晴雨表、风向标。

［1］李至宾.我国股票市场资本配置效率的实证分析［J］.宏观经济研究，2008（8）：60-63.

［2］吴阳.股票市场资本配置效率研究［D］.成都：西南财经大学，2006.

［3］李名义，张东成.我国股票市场资本配置效率研究［J］.北京工商大学学报：社会科学版，2007（4）：15-20.

［4］牛冬梅.中国股票市场资源配置效率［D］.广州：暨南大学，2008.

［5］李勇.我国股票市场资本配置效率实证分析［J］.山西财经大学学报，2009（4）：28-34.

［6］王锦慧，王倩.中国股票市场资源配置效率与经济增长［J］.生产力研究，2010（2）：135-138.

［7］张婉霞.我国资本市场的配置效率分析［D］.太原：山西大学，2011.

［8］金雪军，王永剑.我国资本配置效率影响因素的实证分析［J］.上海金融，2013（8）：23-27.

［9］万艳.中国股票市场资源配置效率研究［D］.南昌：江西财经大学，2012.

［10］张立.台湾地区多层次股票市场及其效率——基于资源配置效率模型的实证分析［J］.金融纵横，2013（12）：47-52.

［11］庞如超.沪深股市与香港股市资本配置效率比较分析［J］.商业时代，2011（2）：62-63.

［12］WURGLER J.Financial Markets and the Allocation of Capital［J］.Journal of Financial Economics，2000，58（1）：187-214.

［13］CHARI A，HENRY P B.Capital Account Liberalization：Allocative Efficiency or Animal Spirits［R］.National Bureau of Economic Research，2002.

［14］GALINDO A，SCHIANTARELLI F，WEISS A.Does financial Liberalization Improve the Allocation of Investment：Micro-evidence from Developing Countries［J］.Journal of Development Economics，2012，83（2）：562-587.

［15］KSIAZEK T G，ERDMAN D，GOLDSMITH C S.A Novel Coronavirus Associated with Severe Acute Respiratory Syndrome［J］.New England Journal of Medicine，2003，348（20）：1953-1966.

［16］CHONG T T L，CHENG S H S，WONG E N Y.A Comparison of Stock Market Efficiency of the BRIC Countries［J］.Technology and Investment，2010，1（4）：235.

（责任编辑 冯 林）

A Comparative Study of Sino-Indian Stock Market Capital Allocation Efficiency

WANG Shukun1，ZHANG Yanliang2
（1.Financial Department，Shandong University of Finance and Economics，Jinan 250014，China；2.School of Finance，Shandong University of Finance and Economics，Jinan 250014，China）

China and India are both emerging market economies in the transitional stage.Indian stock market with a 140-year development history is an Asian model with its capital allocation function playing well，and there exists much experience for China to draw on.Based on Jeffrey Wurgler＇s capital allocation efficiency model and the relevant data selected from the latest decade China and India stock markets，the relationship between stock market financing and economic growth in both countries is analyzed via Granger Causality Test and VAR model，and the results show that GDP and stock market financing present a long-term equilibrium relationship in the two countries while the capital allocation efficiency in India stock market is higher than that in China stock market.

stock market；capital allocation efficiency；Granger Causality Test；VAR model

F830.91

A

2095-929X（2016）01-0022-08

2015-12-15

教育部人文社会科学一般项目“金砖四国股票市场成长能力比较研究（11YJEGJW001）”；山东省金融产业优化与区域金融管理协同创新中心专项资金。

王淑坤，男，山东沂水人，山东财经大学财务处会计师，研究方向：证券市场；张延良，男，山东莱芜人，经济学博士，山东财经大学金融学院教授，研究方向：证券市场，Email：wsk0722@163.com。