卷积定理与傅里叶变换性质及其应用的关系探讨

黄金平,张正炳

(长江大学电子信息学院，湖北 荆州 434023)



卷积定理与傅里叶变换性质及其应用的关系探讨

黄金平,张正炳

(长江大学电子信息学院，湖北 荆州 434023)

为解决学生学习傅里叶变换这部分内容感觉困难的问题，深入研究了傅里叶变换性质之间的内在联系。傅里叶变换的时移性质、时域微分性质、时域积分性质、频移性质、频域微分性质等许多性质只是时域卷积定理和频域卷积定理的特例，而傅里叶变换的独立性质只有线性性质、尺度性质、对偶性质和卷积定理。这一发现对傅里叶变换一章的教学具有重要参考价值，结合傅里叶变换性质内在联系的新教学方案将使得学生学习傅里叶变换的内容不仅易于理解，而且条理清晰，便于记忆，从而解决“傅里叶变换难”的问题。

卷积定理；傅里叶变换；性质；应用

在教学与教研活动中，笔者发现傅里叶变换的性质并非如现存各版本的《信号与系统》[1,2]教材上所编写的看似彼此孤立，而是有着严密数学联系的统一、有机整体。在傅里叶变换的众多性质中，卷积定理有着特别的作用：透过卷积定理不仅能揭示这些性质之间的相互关系，而且可以推导出傅里叶变换在电子技术中的诸多重要应用。为此，笔者试着从卷积定理出发，探讨卷积定理与傅里叶变换性质以及傅里叶变换的几个典型应用之间的关系。

1　卷积定理

卷积定理包括时域卷积定理和频域卷积定理。

定理1(时域卷积定理)若f1(t)⟺F1(jω)，f2(t)⟺F1(jω)，则f1(t)与f2(t)的卷积f1(t)*f2(t)的傅里叶变换为F1(jω)F2(jω)。

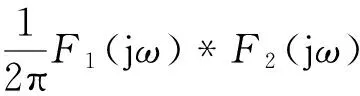
关于这2个定理，可以利用卷积的定义和傅里叶变换的定义[3]很容易得到证明。

2　时域卷积定理与傅里叶变换性质及应用的关系

2.1时域卷积定理与时移性质

在时域中，设f1(t)=f(t)，f2(t)=δ(t-t0)，由于f1(t)*f2(t)=f(t)*δ(t-t0)=f(t-t0)，即时移。

在频域中，设f1(t)=f(t)⟺F(jω)，由于f2(t)=δ(t-t0) ⟺ejωt0，据时域卷积定理得：

f(t-t0)⟺F1(jω)F2(jω)=F(jω)ejωt0

(1)

式(1)就是傅里叶变换的时移性质。

2.2时域卷积定理与微分性质

在时域中，设f1(t)=f(t)，f2(t)=δ′(t)，由于f1(t)*f2(t)=f(t)*δ′(t)=f′(t)，即时域微分。

在频域中，设f1(t)=f(t)⟺F(jω)，由于f2(t)=δ′(t)⟺(jω)，据时域卷积定理得：

f′(t)⟺F1(jω)F2(jω)=jωF(jω)

(2)

式(2)就是傅里叶变换的时域微分性质。

2.3时域卷积定理与积分性质

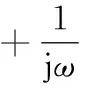
(3)

式(3)就是傅里叶变换的时域积分性质。

2.4时域卷积定理与系统函数

在时域中，设f1(t)=δ(t)，f2(t)=h(t)，由于f1(t)*f2(t)=δ(t)*h(t)=h(t)，即系统冲激响应。

在频域中，由于f1(t)=δ(t)⟺1，由于f2(t)=h(t)⟺H(jω)，据时域卷积定理得：

h(t)⟺F1(jω)F2(jω)=H(jω)

(4)

式(4)就是系统函数[4]。

2.5时域卷积定理与系统的零状态响应

在时域中，设f1(t)=f(t)，f2(t)=h(t)，由于f1(t)*f2(t)=f(t)*h(t)=yzs(t)，即系统零状态响应。

在频域中，设f1(t)=f(t)⟺F(jω)，f2(t)=h(t)⟺H(jω)，据时域卷积定理得：

yzs(t)=h(t)*f(t)⟺F1(jω)F2(jω)=H(jω)F(jω)

(5)

式(5)就是零状态响应的频域分析法[5]。

2.6时域卷积定理与系统的无失真传输条件

在时域中，设f1(t)=f(t)，f2(t)=Kδ(t-t0)，由于f1(t)*f2(t)=f(t)*Kδ(t-t0)=Kf(t-t0)，即系统无失真传输。

在频域中，设f1(t)=f(t)⟺f(jω)，f2(t)=Kδ(t-t0)⟺Kejωt0，据时域卷积定理得：

Kf(t-t0)=Kδ(t-t0)*f(t)⟺F1(jω)F2(jω)=KF(jω)ejωt0

(6)

式(6)就是系统的无失真传输条件。

2.7时域卷积定理与正弦稳态响应

在时域中，设f1(t)=ejω0t，f2(t)=h(t)，由于f1(t)*f2(t)=ejω0t*h(t)=H(jω)ejω0t，即系统正弦稳态响应。

在频域中，设f1(t)=ejω0t⟺2πδ(ω-ω0)，f2(t)=h(t)⟺H(jω)，据时域卷积定理得：

yss(t)=h(t)*f(t)=H(jω)ejω0t⟺F1(jω)F2(jω)=2πδ(ω-ω0)H(jω)

=2πH(jω0)δ(ω-ω0)

(7)

式(7)就是系统正弦稳态响应的频域分析法[5]。

由以上分析可见，根据傅里叶变换的时域卷积定理可推导出如式(1)～(7)所示的傅里叶变换的时移性质、微分性质、积分性质，并能得出系统函数与系统冲激响应的关系、系统零状态响应的求法、解释系统无失真传输条件、系统正弦稳态响应的求法等。这些性质实际上只是时域卷积定理的特例，总结归纳于表1中。

3　频域卷积定理与傅里叶变换性质及应用的关系

3.1频域卷积定理与频移性质

在时域中，设f1(t)=f(t)，f2(t)=e±jω0t，则f1(t)f2(t)=f(t)e±jω0t。

在频域中，设f1(t)=f(t)⟺F(jω)，由于f2(t)=e±jω0t⟺2πδ(ω∓ω0) ，据频域卷积定理得：

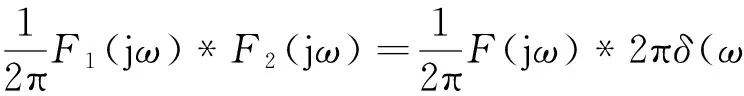
(8)

式(8)就是傅里叶变换的频移性质。

表1　时域卷积定理与傅里叶变换其他性质关系和几个典型应用

3.2频域卷积定理与频域微分性质

在时域中，设f1(t)=f(t)，f2(t)=-jt，则f1(t)f2(t)=-jtf(t)。

在频域中，设f1(t)=f(t)⟺F(jω)，由于f2(t)=-jt⟺2πδ′(ω)，据频域卷积定理得：

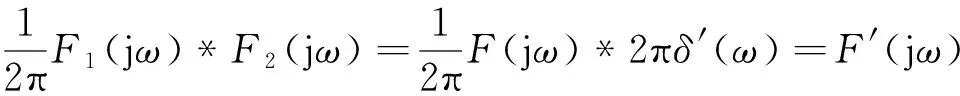
(9)

式(9)就是傅里叶变换的频域微分性质。

3.3频域卷积定理与调制

在时域中，设f1(t)=f(t)，f2(t)=cosω0t，则f1(t)f2(t)=f(t)cosω0t，即振幅调制。

在频域中，设f1(t)=f(t)⟺F(jω)，由于f2(t)=cosω0t⟺π[δ(ω-ω0)+δ(ω+ω0)]，据频域卷积定理得：

(10)

式(10)就是振幅调制定理[3]。

由以上分析可见，据傅里叶变换的频域卷积定理可推导出如式(8)～(10)所示的傅里叶变换的频移性质、频域微分性质，并能得出指导通信实践的振幅调制定理。这些性质归纳于表2。

4　结语

在多年的教学实践和长江大学省级精品资源共享课程《信号与系统分析》的建设实践中，为解决学生对傅里叶变换这一章内容学习困难的问题，笔者所在教学团队积极开展研究和探索，结合傅里叶变换性质之间的内在联系，摸索出了一套的新的讲授方案，具体讲授次序依次为：先提出傅里叶变换的定义，

[1]奥本海姆 (美).信号与系统[M].第3版.刘树棠译.北京：电子工业出版社，2013.

[2] 郑君里.信号与系统[M].第3版.北京：高等教育出版社，2014.

[3] 金波,张正炳.信号与系统分析[M].北京：高等教育出版社，2011.

[4] 管致中,夏恭恪,孟桥.信号与线性系统[M].第5版.北京：高等教育出版社，2014.

[5] 张小虹.信号与系统[M].第2版.陕西：西安电子电子科技大学出版社，2012.

[6] 沈元隆,周井泉.信号与系统[M].北京：人民邮电出版社，2007.

[编辑]洪云飞

2016-04-23

湖北高校省级精品资源共享课程。

黄金平(1965-),男,副教授,现主要从事电子与信息方面的教学与研究工作；E-mail:1103934907@qq.com。

O441

A

1673-1409(2016)19-0029-03

[引著格式]黄金平,张正炳.卷积定理与傅里叶变换性质及其应用的关系探讨[J].长江大学学报(自科版)，2016,13(19)：29～31，41.