电离层高阶项改正对我国陆态网测站坐标的影响

余新平　成英燕　邱荣海　曹炳强　李晓光,3

1　山东科技大学测绘科学与工程学院，青岛市前湾港路579号, 266000 2　中国测绘科学研究院，北京市莲花池西路28号，100830 3　辽宁工程技术大学测绘与地理科学学院，阜新市玉龙路88号，123009



电离层高阶项改正对我国陆态网测站坐标的影响

余新平1,2成英燕2邱荣海1,2曹炳强2李晓光2,3

1山东科技大学测绘科学与工程学院，青岛市前湾港路579号, 266000 2中国测绘科学研究院，北京市莲花池西路28号，100830 3辽宁工程技术大学测绘与地理科学学院，阜新市玉龙路88号，123009

摘要：通过不同的方案设计对中国陆态网测站进行解算，研究电离层高阶项延迟对测站坐标和接收机钟差的影响，并分析在不同地磁模型下的影响差异。结果表明，在太阳活动较为活跃时，电离层高阶项延迟对陆态网测站垂向坐标的影响能达到1.2 cm，对接收机钟差的影响接近4.4 mm；不同地磁模型下电离层高阶项延迟的影响很小。还分析了纬度、基线方向与长度对电离层高阶项延迟的影响。

关键词：电离层高阶项延迟； 地磁模型； 陆态网测站； 基线

电离层延迟是GNSS测量的主要误差源之一,高精度精密定位时大多采用双频技术(消电离层组合观测值)来削弱其影响,但仅能消除电离层一阶项延迟的影响，剩下的高阶项影响仍能达到2～4 cm[1]。虽然理论上可以利用三频观测的线性组合进一步消除电离层二阶项延迟,但由于组合后的观测噪声影响被过分放大,实际中无法直接应用[2]。本文通过对我国陆态网测站连续3 a的双频GPS观测数据进行分析，研究电离层高阶项延迟改正对陆态网测站坐标的影响及其在不同地磁模型下的差异。

1　电离层高阶项延迟的基本原理

GPS载波相位观测值和伪距观测值所受电离层延迟影响为：

(1)

式中，I(1)、I(2)、I(3)分别为电离层延迟中的一阶项、二阶项、三阶项，可表示为：

(2)

式中，μ0为真空中的磁导率，取12.57×10-7H/m；e为真空中的介电系数，取8.854 2×10-12F/m；ε0为每个电子所带的电荷，取1.602 1×10-19C；me为电子的质量，取9.109 6×10-31kg；TEC为信号传播路径中的总电子含量，可用双频观测值来确定，也可用电离层模型进行估计；H为地磁场强度，可根据地磁场模型来计算；θ为地磁场强度矢量与卫星信号传播方向之间的夹角，卫星信号传播方向可根据测站的近似坐标及卫星星历(或卫星历书)来确定；N为总电子含量。由于二阶项和三阶项均为微小量，因而可将整个电离层压缩为一个单层，用以代替整个电离层。通常将电离层单层模型高度设定为300～450 km，本文取450 km。

在顾及电离层高阶延迟项影响时，通常利用LC双频组合观测技术来消除电离层一阶延迟项的影响。双频载波相位观测组合为：

(3)

2　实例分析

由式(2)可知，求得总电子含量、地磁场强度及其与卫星信号间的夹角θ，便可得到电离层高阶项延迟的改正量。通过GPS伪距和载波相位观测量，可得到传播路径上较为精确的电离层总电子含量[3]。在分析电离层高阶项延迟影响时，暂不考虑总电子含量的影响。

目前GAMIT10.5提供的地磁模型有两种：国际地磁标准参考场IGRF模型(包括IGRF10和IGRF11)和同心倾斜磁偶极子模型DIPOLE。IGRF模型是一个通过全球地磁场资料的高斯分析得出的全球地磁场数值模型；而DIPOLE模型是以赤道附近的地磁场强为基准，通过计算某点的地磁余纬度求得该点的地磁场强值,是一个近似模型[4-6]。

2.1数据准备

基于IGS以及陆态网提供的数据服务，从中选取不同纬度且主要位于西南、华北、沿海等地震高发地带、分布较为均匀的13个站点，包括ZJZS、FJXP、SDJX、HEZJ、HBXF、SNAK、GZFG、NMWH、GSJT、YNMJ、SCYY、QHMQ、XJSS，并以BJFS、WUHN、URUM、SHAO等12个IGS站点作为控制站，如图1(星号表示IGS测站，点号表示陆态网测站)。鉴于测站上空电离层总电子含量每年都发生变化，因此以半年左右为一个观测周期，从中选择2011～2013年每年1月和6月的双频实测数据进行解算，并利用LC组合观测消除电离层一阶延迟项，以此来分析电离层高阶项延迟对陆态网测站坐标的影响。

由于目前陆态网可同时接收多个系统的观测数据，而GAMIT10.5只能解算GPS数据，所以在解算之前需用TEQC软件移去多余观测类型的数据，并检查多路径效应的影响。

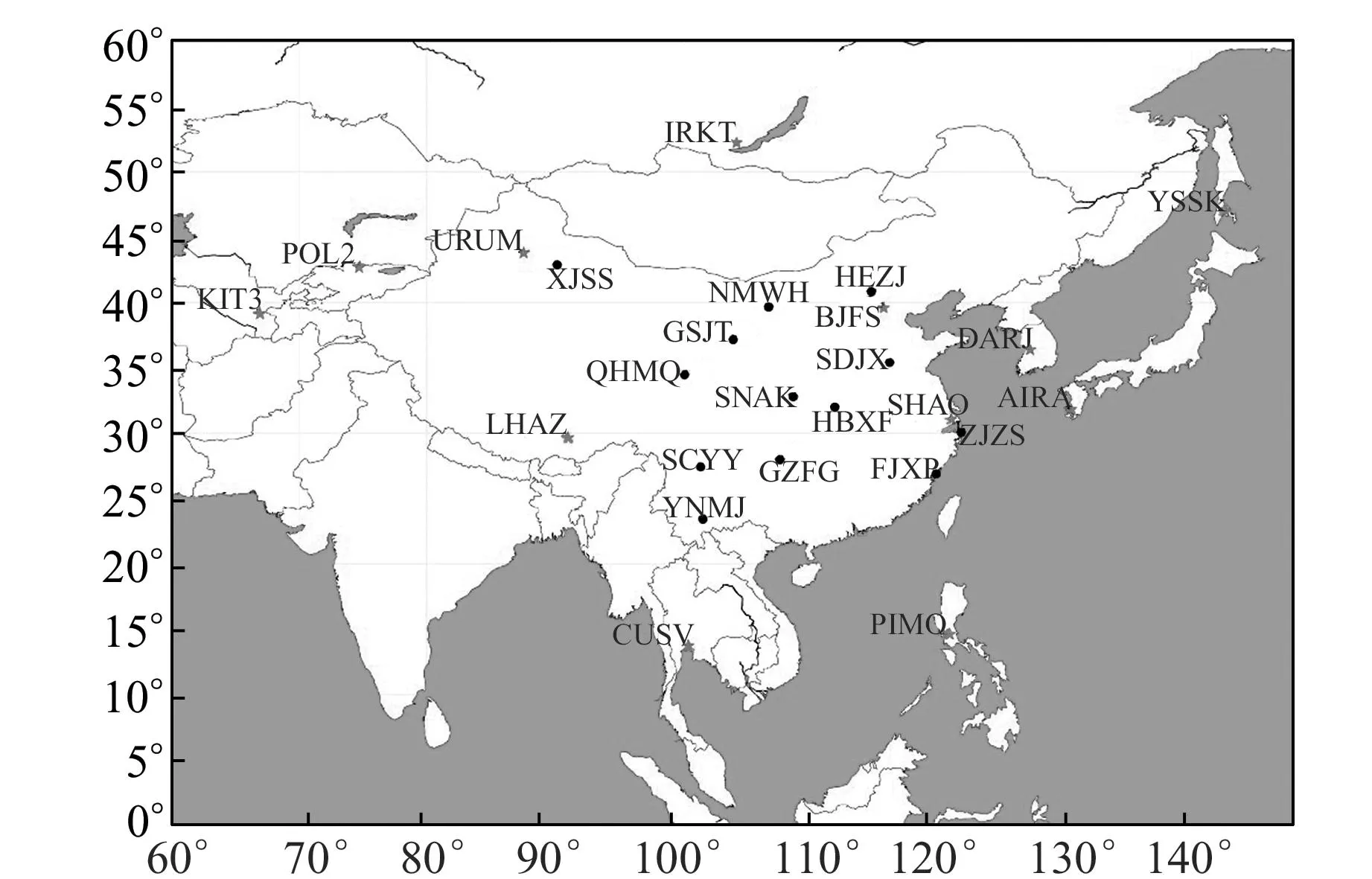
图1　IGS及陆态网站点分布Fig.1　The distribution of IGS and CMONOC stations

2.2解算策略

主要参数设置如下：电离层延迟模型为消电离层的LC组合观测；处理模式为松弛解RELAX；卫星截止高度角取15°，以避免多路径效应等与卫星高度角有关的误差影响；电离层模型和地磁模型根据方案设计的不同作相应调整。

为了更好地分析电离层高阶项延迟对陆态网测站坐标和接收机钟差的影响，及其在不同地磁模型下的差异，本文通过以下3种方案对陆态网测站数据进行处理：1)电离层模型设为NONE，地磁模型设为IGRF11；2)电离层模型设为GMAP(即加入电离层高阶项延迟改正)，地磁模型设为IGRF11；3)电离层模型设为GMAP，地磁模型设为DIPOLE。

2.3结果分析

如图2所示，顾及与不顾及电离层高阶项延迟改正对陆态网测站3个方向坐标变化的影响基本一样，且地磁模型的改变也不会影响其变化趋势。但随着模型的改变，陆态网测站坐标值的变化会有较大差异。

图2　电离层高阶项延迟对HBXF坐标的影响Fig.2　Effect of high order term delay on HBXF coordinates

2.3.1电离层高阶项延迟影响分析

将方案2与方案1的差值表示为GM-NO(即只考虑电离层高阶项延迟改正的影响),方案3与方案2的差值表示为DI-IT(即只考虑不同地磁模型的影响)。如图3所示，GM-NO与DI-IT随时间的变化均呈山峰状走势，且前者比后者大2倍多。GM-NO在N、E、U方向的均值分别为3.0 mm、1.8 mm、7.3 mm，而DI-IT的均值则为0.9 mm、0.7 mm、1.5 mm。

同时在2012-06，差值GM-NO与DI-IT均达到峰值，这可能是受太阳活跃程度的影响，因为2012年正是太阳活动剧烈期。2012-06差值GM-NO亦即电离层高阶项延迟，在太阳活跃期对陆态网测站水平方向的影响在5 mm左右，对垂直方向的影响也只有1.2 cm。这对于一般工程应用可以忽略，但对主要用于地震监测的陆态网测站则必须考虑。

2.3.2地磁模型影响分析

如图3所示，以HBXF为例，在以不同方式建立的表征全球地磁场强度变化的地磁模型ITRF11和DIPOLE下，电离层高阶项延迟对陆态网测站水平方向的影响还不到1 mm，在太阳活跃期的2012-06对垂直方向的影响也只有不到4 mm。因此，一般情况下可以忽略地磁模型对陆态网测站的影响。

图3　差值GM-NO和DI-IT趋势图Fig.3　The difference between GM-NO and DI-IT trend chart

3　电离层高阶项延迟对接收机钟差的影响

按照上述同样的解算策略，差值GM-NO为只考虑电离层高阶项延迟改正的影响，差值DI-IT为只考虑不同地磁模型的影响，通过这两个差值来定量表征电离层高阶项延迟和地磁模型对接收机钟差的影响。

从表1可知，电离层高阶项延迟对陆态网测站接收机钟差的影响在4.4 mm左右，并随测站纬度的降低而减小，最大值为新疆XJSS站的5.226 mm，最小值为云南YNMJ站的3.723 mm。这与刘西凤等[11]对不同纬度测站接收机钟差所受电离层高阶项延迟影响的分析结果接近。而在不同的地磁模型下，电离层高阶项延迟对陆态网测站接收机钟差的影响则小很多，其均值为0.037 mm，最大不超过0.093 mm。因此，对于一般精度要求不是很高的形变监测工作，地磁模型的改变对接收机钟差的影响可以忽略。

表1　GM-NO和DI-IT对陆态网站点接收机钟差的影响

4　电离层高阶项延迟对基线向量的影响

电离层高阶项延迟主要由信号传播路径上的地磁场强及总电子含量决定[9]，而总电子含量在全球上空分布不均匀且每年都在变化，地磁场强也会由于纬度的不同而有所差异。所以，随着基线所处纬度及其长度和方向的变化，电离层高阶项延迟影响也会产生相应变化。

4.1电离层高阶项延迟与基线方向的关系

本文通过对sigma值的变化，来分析电离层高阶项延迟与基线所处纬度及其长度和方向的关系。sigma值越小，基线解算精度则越高。

从陆态网测站和IGS站找出3条纬度和长度大体相同但方向不同的基线，它们分别是东西向的SNAK-SDJX基线、南北向的SDJX-HEZJ基线和东南-西北向的SNAK-GSJT基线。将GMAP+ITRF11和NONE+ITRF11模型下分别解算的基线误差作差，能更加直观地看出电离层高阶项延迟对基线解算精度的影响。

从表2可以看出，南北向的SDJX-HEZJ基线解算精度受电离层高阶项延迟的影响最大，均值达到6.41 mm；东南-西北向的SNAK-GSJT基线次之，在4.60 mm左右波动；东西向的SNAK-SDJX基线受到的影响最小，均值仅为1.3 mm。其原因可能在于东西方向总电子含量变化比较平缓，而在南北方向则变化较为剧烈[6-7]。

4.2电离层高阶项延迟与基线长度的关系

为了分析电离层高阶项延迟对不同长度基线的影响，在中纬度地区选取方向皆为西南-东北向的3条基线进行解算。如表3所示，随着基线长度的增加，基线解算误差越来越大，当基线长度在2 000 km以上时，电离层高阶项延迟对基线解算精度的影响可达8 mm左右。这是由于基线两端测站上的总电子含量随着基线长度的增加而不断增大[8-10]。

4.3电离层高阶项延迟与基线所在纬度的关系

从解算的所有基线中选择3条东西向且长度接近的基线，分别为位于高纬度地区的XJSS-POL2基线、中纬度地区的SDJX-QHMQ基线和低纬度地区的FJXP-GZFG基线。从表4可以看出，随着纬度的降低，电离层高阶项延迟对基线解算精度的影响不断增加，对低纬度地区的FJXP-GZFG基线的影响为3.54 mm左右。这是由于总电子含量在赤道附近取极大值，并且随着纬度的增加而减小[11-12]。

表2　电离层高阶项延迟对不同方向基线的影响

表3　电离层高阶项延迟对不同长度基线的影响

表4　电离层高阶项延迟对不同纬度基线的影响

5　结　语

本文利用GAMIT10.5对我国陆态网测站进行解算，通过3种不同的方案设计，研究电离层高阶项延迟对陆态网测站坐标和接收机钟差的影响，并分析在不同地磁模型下电离层高阶项延迟对陆态网测站的影响差异。

1)电离层高阶项延迟对陆态网测站水平坐标影响很小，N、E方向均值分别为3.0 mm、1.8 mm，但对垂直方向坐标影响均值为7.3 mm。在太阳活动较为活跃的2012-06，其对水平坐标的影响均小于5 mm，但对垂向坐标的影响达到1.2 cm。

2)电离层高阶项延迟对陆态网测站接收机钟差的影响在4.4 mm左右，并随测站纬度的降低而减小。

3)在不同的地磁模型影响下，电离层高阶项延迟对陆态网测站坐标影响的差异很小，水平方向皆不足1 mm，垂直方向也只有1.5 mm；其对接收机钟差的影响亦只有约0.04 mm。一般情况下，可忽略地磁模型改变所带来的影响。

本文还讨论了纬度、基线方向与长度对电离层高阶项延迟的影响。结果表明，南北向的基线解算精度受电离层高阶项延迟的影响最大，东西向基线最小；随着基线长度的增加，电离层高阶项延迟对基线解算精度的影响越来越大；随着基线所处纬度的降低，电离层高阶项延迟对基线解算精度的影响不断增加。因此，在分析电离层高阶项延迟对陆态网测站坐标的影响时，应充分考虑与基线相关的因素。

参考文献

[1]魏子卿，葛茂荣.GPS相对定位的数学模型[M]．北京：测绘出版社，1998(Wei Ziqing,Ge Maorong.Mathematical Model of GPS Relative Positioning[M]. Beijing: Surveying and Mapping Press, 1998)

[2]袁运斌, 霍星亮, 欧吉坤. 精确求定 GPS 信号电离层延迟模型与方法研究[J]. 自然科学进展, 2006, 16(1): 40-48(Yuan Yunbin, Huo Xingliang, Ou Jikun. Study on Model and Method of Ionospheric Delay for Calculating Exactly GPS Signal[J]. Progress in Natural Science, 2006, 16 (1): 40-48)

[3]袁运斌. 基于 GPS 的电离层监测及延迟改正理论与方法的研究[D].武汉: 中国科学院测量与地球物理研究所, 2002(Yuan Yunbin. Study on Theories and Method of Correction Ionospheric Delay and Monitoring Ionosphere Based on GPS[D].Wuhan: Institute of Geodesy and Geophysics, CAS, 2002)

[4]黄晓颖，边少锋．国际高精度地磁模型研究进展[J]．海洋测绘,2010,30(3):79-82 (Huang Xiaoying, Bian Shaofeng. The Research Evolution of International High- resolution Geomagnetic Model[J]. Hydrographic Surveying and Charting, 2010,30 (3):79-82)

[5]陈斌，顾左文，狄传芝,等.第11代国际地磁参考场[J].国际地震动态,2012,398(2):20-27(Chen Bin,Gu Zuowen,Di Chuanzhi,et al.International Geomagnetic Reference Field: the Eleventh Generation[J]. Recent Development in World Seismology,2012,398(2):20-27)

[6]朱春春，李征航.高阶电离层延迟对GPS双差观测值和基线向量的影响[J].大地测量与地球动力学，2015,35(1)：81-86(Zhu Chunchun, Li Zhenghang.Higher-Order Ionospheric Effects on GPS Double Difference Observation and Baseline Vector[J].Journal of Geodesy and Geodynamics,2015,35 (1):81-86)

[7]张小红，李征航，蔡昌盛．用双频GPS观测值建立小区域电离层延迟模型研究[J]．武汉大学学报:信息科学版，2001,26(2):140-146(Zhang Xiaohong, Li Zhenghang, Cai Changsheng.Study on Regional Ionospheric Model Using Dual-frequency GPS Measurements[J].Geomatics and Information Science of Wuhan University, 2001,26(2):140-146)

[8]Brunner F K.An Improved Model for the Dual Frequency Ionospheric Correction of GPS Observation[J].Manuscripta Geodaetica,1991,16:205-214

[9]李征航，陈锴，刘万科,等．顾及f3项的电离层延迟模型[J].武汉大学学报:信息科学版，2007,32(2):139-143(Li Zhenghang, Chen Kai, Liu Wanke, et al.Ionospheric Delay Model Containingf3Term[J].Geomatics and Information Science of Wuhan University, 2007,32(2):139-143)

[10] 刘西凤，袁运斌，霍星亮,等．电离层二阶项对GPS定位影响的分析模型与方法[J]．科学通报，2010,55(12):1 162-1 167(Liu Xifeng, Yuan Yunbin, Huo Xingliang, et al. Model Analysis Method(MAM) on the Effect of the Second-order Ionospheric Delay on GPS Positioning Solution[J].Chinese Science Bull, 2010,55(12): 1 162-1 167)

[11] 刘西凤，袁运斌．我国中低纬地区GPS定位中的电离层二阶项延迟影响分析与研究[J]．中国科学，2010,40(5):658-662(Liu Xifeng, Yuan Yunbin. Preliminary Analysis on the Effect of the Second-order Ionospheric Delay on GPS Positioning Solution Over the Mid-Low Latitude Regions in China[J]. Science in China,2010,40(5): 658-662)

[12] 邓连生.电离层高阶项延迟对GPS坐标时间序列影响的研究[D]．武汉：武汉大学，2012(Deng Liansheng. Study on the Effect of the Second-order Ionospheric Delay on GPS Coordinate Time Series[D].Wuhan: Wuhan University, 2012)

Foundation support:National Natural Science Foundation of China,No. 41374014,41404034.

About the first author:YU Xinping, postgraduate, majors in the data processing and time series analysis of GPS,E-mail:862250281@qq.com.

收稿日期：2016-01-31

第一作者简介：余新平，硕士生，主要研究方向为GPS数据处理及时间序列分析，E-mail:862250281@qq.com。

DOI：10.14075/j.jgg.2016.08.013

文章编号：1671-5942(2016)08-0714-05

中图分类号：P228

文献标识码：A

Analysis of Higher-order Ionospheric Effects on CMONOC Coordinate Variations

YUXinping1,2CHENGYingyan2QIURonghai1,2CAOBingqiang2LIXiaoguang2,3

1College of Geomatics, Shandong University of Science and Technology, 579 Qianwangang Road, Qingdao 266000,China2Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road,Beijing 100830,China3School of Mapping and Geographical Science, Liaoning Technical University,88 Yulong Road,Fuxin 123009,China

Abstract:By designing different scenarios, we can solve stations of CMONOC, in order to analyze the influences of higher-order terms ionospheric delay and receiver clock error to CMONOC stations’ coordinates, and the differences of higher-order terms ionospheric delay's effect under different geomagnetic models. The results show that as solar activity becomes more active, the change of higher-order terms ionospheric delay to CMONOC stations' vertical coordinates can reach 1.2 cm. The influence on the receiver clock error is close to 4.4 mm, the influences of the higher-order ionospheric delay model under different geomagnetic conditions are little. Finally, we discuss and analyze the effect of latitude, baseline length and direction to the higher-order terms ionospheric delays.

Key words:higher-order terms ionospheric delay; geomagnetic model; CMONOC; baseline

项目来源：国家自然科学基金(41374014，41404034)。